Fixed Income portfolio management quantifying measuring interest rate

Fixed Income portfolio management: - quantifying & measuring interest rate risk Interest rate risk measures: Duration Convexity PVBP Interest Rate Risk Management Finance 30233, Fall 2010 S. Mann

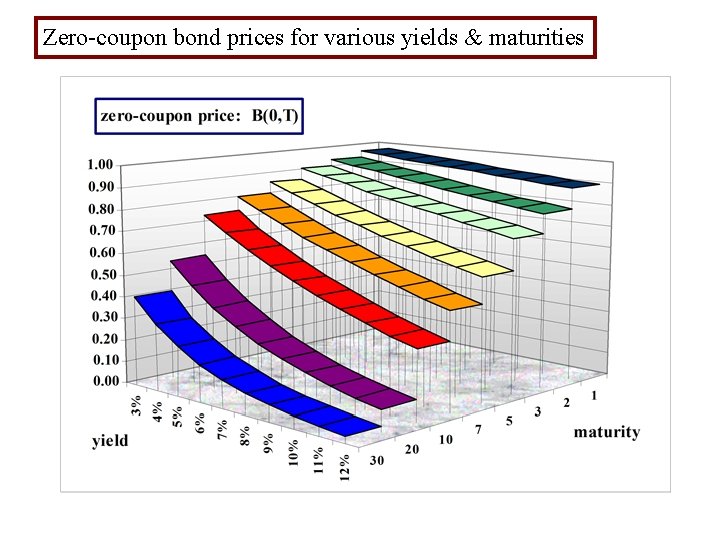
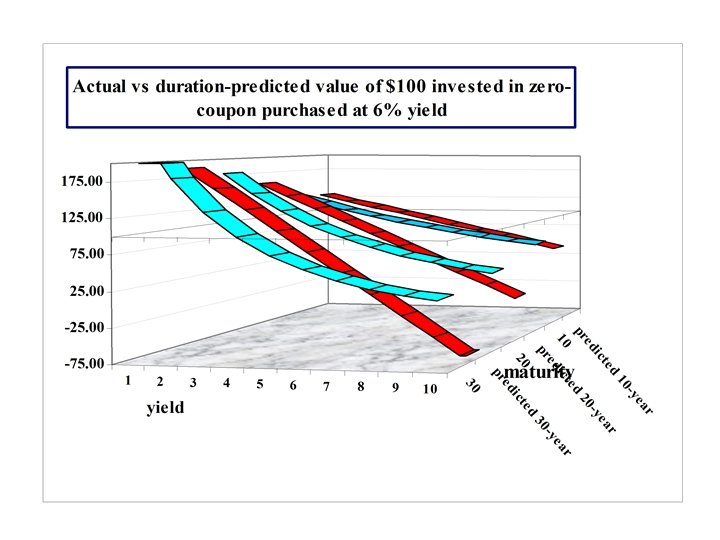
Zero-coupon bond prices for various yields & maturities

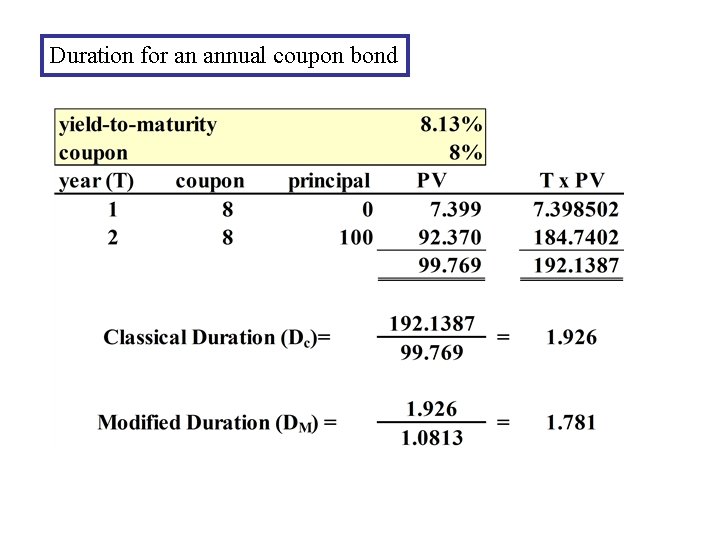
Duration Bond price (Bc) as a function of yield (y): Small change in y, Dy, changes bond price by how much? Classical duration weights each cash flow by the time until receipt, then divides by the bond price:

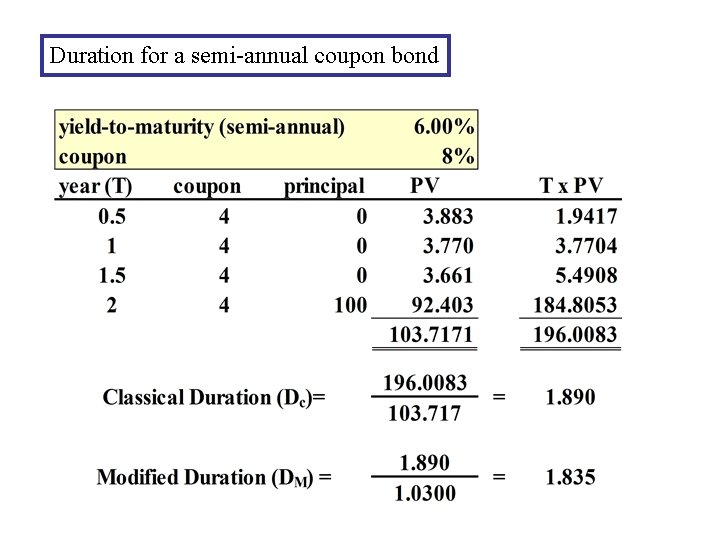
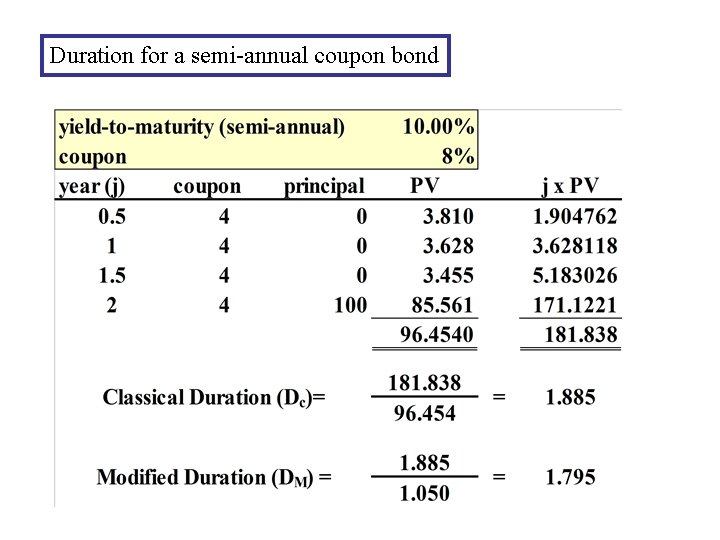
Modified Duration Define DM = Dc /(1+y) (annual coupon) = Dc /(1+y/2) (semi-annual coupon) ( modified duration) approximate % change in Price: DP/P = - DM x Dy example: DM = 4. 5 Dy= + 30 bp expected % price change= -4. 5 (. 0030) = -1. 35% linear approximation. Convexity matters.

Modified duration Percentage change in bond price: Modified Duration (DM): DM = Dc/(1+y) DM = Dc/(1+y/2) Change in bond price: Duration is linear approximation (annual coupon) (semiannual coupon)

Duration for an annual coupon bond

Duration for a semi-annual coupon bond

Duration for a semi-annual coupon bond

Price Value of Basis Point (PVBP) PVBP = DM x Value x. 0001 Example: portfolio value = $100, 000; DM = 4. 62 PVBP = (4. 62) x 100, 000 x. 0001 = $46. 20 Exercise: estimate value of portfolio above if yield curve rises by 25 bp (in parallel shift). Food for thought: what about non-parallel shifts?

Convexity: adjusting for non-linearity Predicted % price change using duration: DP/P = -Dm Dy Duration is FIRST derivative of bond price. (slope of curve) convexity is SECOND derivative of bond price (curvature: change in slope) Using duration AND convexity, we can estimate bond percentage price change as: DP/P = - Dm. Dy + (1/2) Convexity (Dy)2 (a 2 nd order Taylor series expansion) (the convexity adjustment is always POSITIVE) (We will not hand-calculate convexity)

Example using Convexity example: 30 year, 8% coupon bond with y-t-m of 8%. Modified duration = 11. 26, Convexity = 212. 4 What is predicted % price change for increase of yield to 10%? Duration prediction: DP/P = - Dm. Dy = -11. 26 x 2. 0% = -22. 52% Duration & convexity prediction: DP/P = - Dm. Dy + (1/2) Convexity (Dy)2 = -11. 26 x 2. 0% + (1/2) 212. 4 (. 02)2 = -22. 52% + 4. 25% = -18. 27% Actual % price change: price at 8% yield = 100; price at 10% yield = 81. 15. % change = -18. 85%

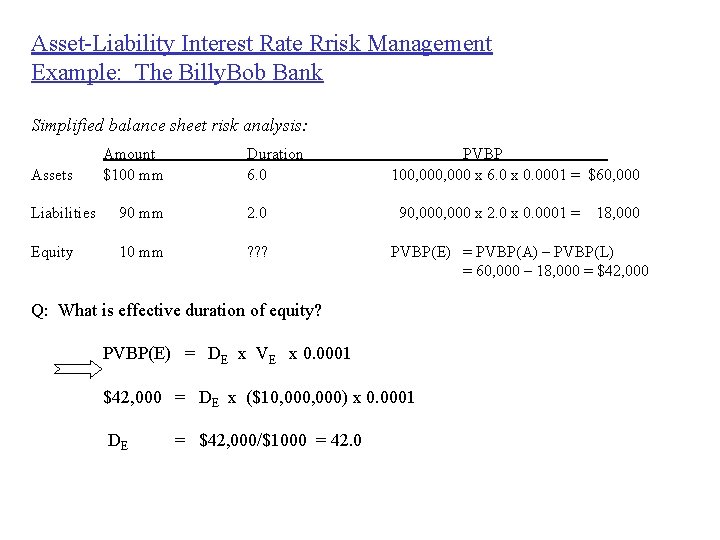
Asset-Liability Interest Rate Rrisk Management Example: The Billy. Bob Bank Simplified balance sheet risk analysis: Assets Amount $100 mm Duration 6. 0 Liabilities 90 mm 2. 0 Equity 10 mm ? ? ? PVBP 100, 000 x 6. 0 x 0. 0001 = $60, 000 90, 000 x 2. 0 x 0. 0001 = PVBP(E) = PVBP(A) – PVBP(L) = 60, 000 – 18, 000 = $42, 000 Q: What is effective duration of equity? PVBP(E) = DE x VE x 0. 0001 $42, 000 = DE x ($10, 000) x 0. 0001 DE = $42, 000/$1000 = 42. 0 18, 000

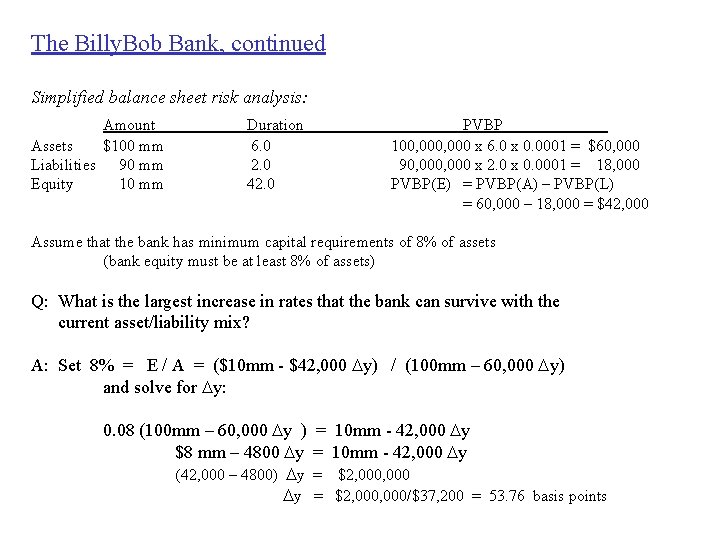
The Billy. Bob Bank, continued Simplified balance sheet risk analysis: Amount Assets $100 mm Liabilities 90 mm Equity 10 mm Duration 6. 0 2. 0 42. 0 PVBP 100, 000 x 6. 0 x 0. 0001 = $60, 000 90, 000 x 2. 0 x 0. 0001 = 18, 000 PVBP(E) = PVBP(A) – PVBP(L) = 60, 000 – 18, 000 = $42, 000 Assume that the bank has minimum capital requirements of 8% of assets (bank equity must be at least 8% of assets) Q: What is the largest increase in rates that the bank can survive with the current asset/liability mix? A: Set 8% = E / A = ($10 mm - $42, 000 Dy) / (100 mm – 60, 000 Dy) and solve for Dy: 0. 08 (100 mm – 60, 000 Dy ) $8 mm – 4800 Dy (42, 000 – 4800) Dy Dy = 10 mm - 42, 000 Dy = $2, 000, 000/$37, 200 = 53. 76 basis points