Classes of Polygons Planar polygons Simple Convex Starshaped

Classes of Polygons • Planar polygons – Simple • Convex • Star-shaped – Non-simple • Non-planar polygons

Planar Polygons • Definition: All points of the polygon must lie within a plane.

Simple Polygons • Definition A polygon P is simple, if no two non-consecutive edges intersect. Simple Not simple

Simple Polygons • The polygon interior is well-defined. If we traverse the polygon in a counter-clockwise direction, the interior is always to our left. Simple Not simple

Convex Polygons • Definition A polygon P is convex, if and only if, for any pair of points x, y, in P the line segment between x and y lies entirely in P. Every point can see every other point. Convex Concave

Convex Polygons • Alternative Definition Going from point Pi to Pi+1 involves making only left had turns. Implies that the polygon vertices are ordered in a counter-clockwise fashion. Implies cross-products of adjacent edges are positive. • Convex polygons are of course, simple.

Triangles • Any three non-colinear points determine a triangle. – Planar – Convex • Cross products can determine the normal (A, B, C)T to the triangle (plane). • Plane: Ax + By + Cz + D = 0, where D can be solved using any of the three points.

Star-Shaped Polygons • Definition A star-shaped polygon, P, is a simple polygon which contains a non-empty set, K of points, such that every point in K is visible from any other point in the polygon. The set K is called the kernel of P. A convex polygon is a star-shaped polygon whose kernel is equal to the interior of P.

Star-Shaped Polygons • The kernel can easily be determined by clipping the polygon to the half-planes defined by each edge.

Non-Planar Polygons • In 3 D computer graphics, we often have to deal with non-planar polygons. – Longitude/latitude grid on a sphere. – Polygonal approximations to smooth surfaces.

More Polygonal Definitions • Convex Hull – The convex hull of a polygon P, is the smallest convex polygon that contains P. • Diagonal – A line segment lying entirely inside polygon P and joining two non-consecutive vertices pi and pk • Principal vertex – A vertex pi of simple polygon P is called a principal vertex if the diagonal (pi-1, pi+1) intersects the boundary of P only at pi-1 and pi+1. Not a principal vertex diagonal Convex hull

More Polygonal Definitions • Ear – A principal vertex pi of a simple polygon P is called an ear if the diagonal (pi-1, pi+1) lies in the interior of P. • Mouth – A principal vertex pi of a simple polygon P is called a mouth if the diagonal (pi-1, pi+1) lies in the exterior of P.

Some Theorems • One-Mouth Theorem – Except for convex polygons, every simple polygon has at least one mouth. • Two-Ears Theorem – Except for triangles, every simple polygon has at least two non-overlapping ears.

Polygonal Tricks • Area • Test for concave/convex.

Polygonal Area • Convex polygons Take any point inside the polygon and compute the area of all triangles formed with one edge and the point. Actually, we can take any point and do this, if we give the area of the triangles a signed value.

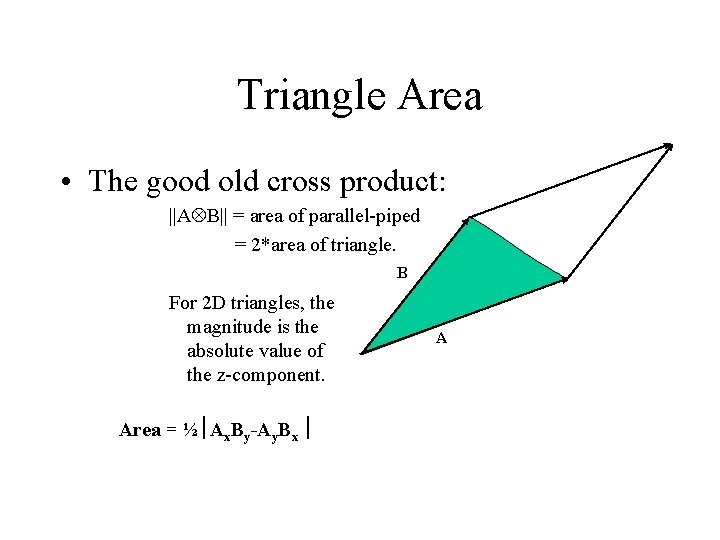
Triangle Area • The good old cross product: ||A B|| = area of parallel-piped = 2*area of triangle. B For 2 D triangles, the magnitude is the absolute value of the z-component. Area = ½ Ax. By-Ay. Bx A

Polygonal Area • Vectors: Choose the point to be the origin, then the vectors are simply the points on the polygon. • Convex polygon Area =

Polygonal Area • Wow!!! This actually works for any simple polygon.

Convexity Test • We can easily determine whether a polygon is convex or concave, and whether it is order clockwise or counter-clockwise. – Examine the cross products between adjacent edges. If they are all the same sign, then the polygon is convex, otherwise it is concave. – If the area computed as before is positive, then the ordering is in a counter-clockwise fashion.

Efficient Scan-Conversion • Convex polygons • Triangles

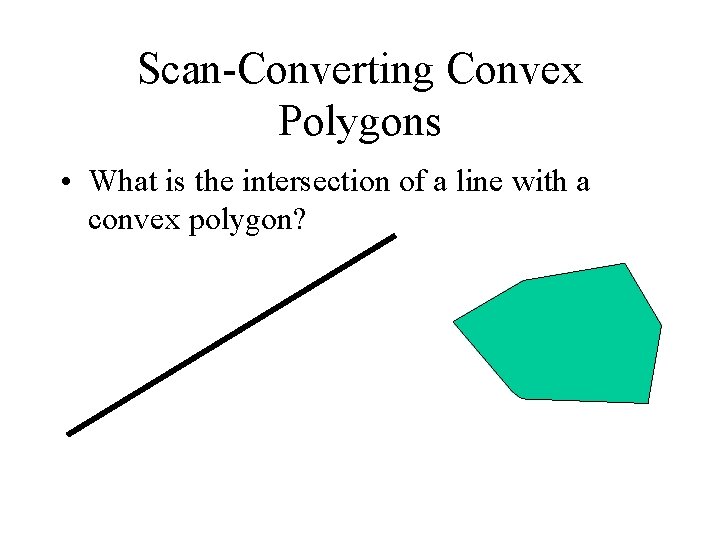
Scan-Converting Convex Polygons • What is the intersection of a line with a convex polygon?

Scan-Converting Convex Polygons • Any line will intersect a convex polygon in at most 2 locations. – This greatly simplifies our active edge table. – Simply keep a current x-left and an x-right intersection. – Update the slopes on scanlines where new edges start.

Scan-Converting Triangles • Special cases One horizontal edge. • For y=ymin to ymax Draw from x-left to x-right Update x-left and x-right

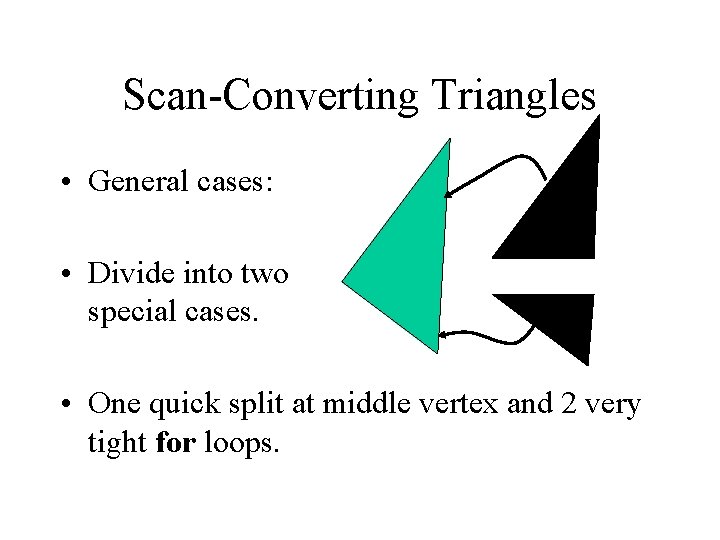
Scan-Converting Triangles • General cases: • Divide into two special cases. • One quick split at middle vertex and 2 very tight for loops.

Triangulations • To avoid problems with non-planar polygons, as well as simplify the scanconversion process, we can triangulate a polygon before we rasterize it. • A triangulation of a simple polygon P consists of n-3 diagonals, or n-2 triangles.

Triangulation Algorithms • Convex polygons are trivial. • Star-shaped polygons can also be dealt with rather easily. • Can also use splitting algorithms as described in the book. These additional vertices, but may be simpler.

Triangulating Convex Polygons • Pick any vertex i. • Connect the vertices (i, k, k+1) for all k i, i-1.

Triangulating Concave Polygons While polygon P is not a triangle Find an ear of P. Remove the ear from P.