Student recommended videos POLAR COORDINATES MIT Polar Coordinates








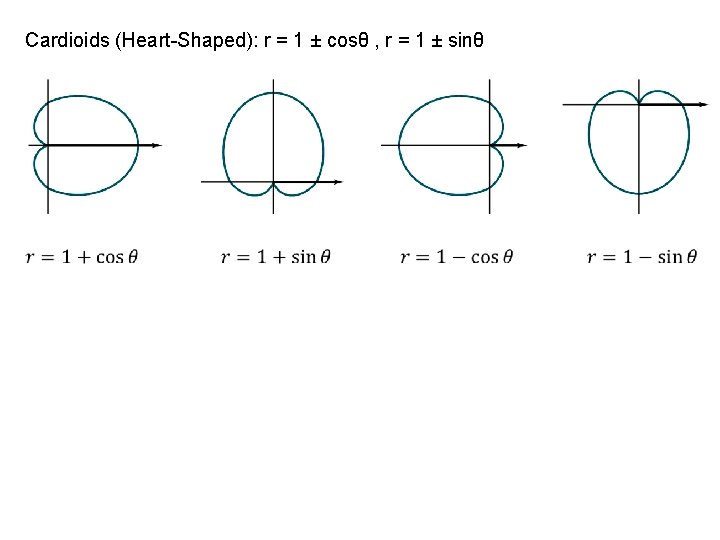

















- Slides: 39

Student recommended videos POLAR COORDINATES MIT – Polar Coordinates click Patrick. JMT Polar coordinates – the Basics click Graphing Polar Curve – Part 1 click Graphing Polar Curve – Part 2 click Areas and Polar Coordinates click

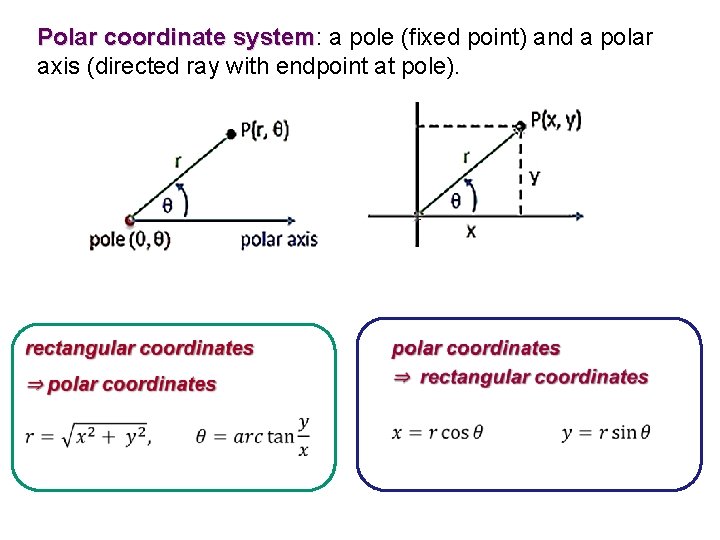
One way to give someone directions is to tell them to go three blocks East and five blocks South ⇒ Cartesian coordinates Another way to give directions is to point and say “Go a half mile in that direction ⇒ Polar coordinates Polar graphing is like the second method of giving directions. Each point is determined by a distance and an angle.

Polar coordinate system: a pole (fixed point) and a polar system axis (directed ray with endpoint at pole).

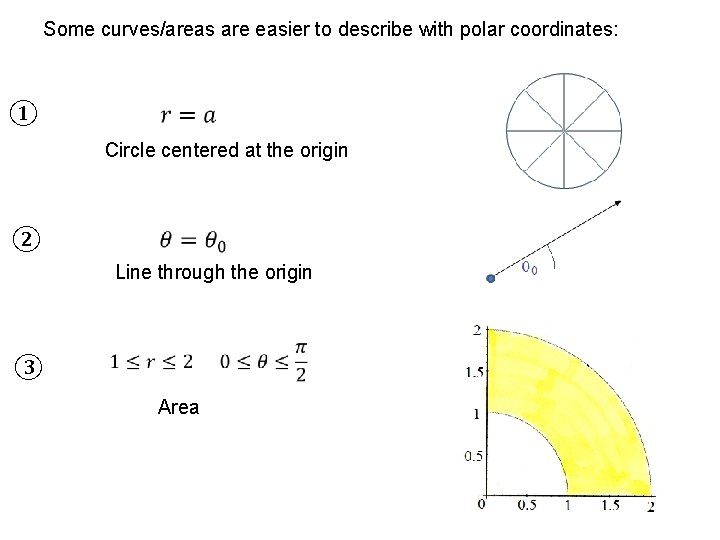
Some curves/areas are easier to describe with polar coordinates: ① Circle centered at the origin ② Line through the origin ③ Area

More than one coordinate pair can refer to the same point. The angle, θ, is measured from the polar axis to a line that passes through the point and the pole. If the angle is measured in a counterclockwise direction, the angle is positive. If the angle is measured in a clockwise direction, the angle is negative. The directed distance, r, is measured from the pole to point P. If point P is on the terminal side of angle θ, then the value of r is positive. If point P is on the opposite side of the pole, then the value of r is negative.

Example All of the polar coordinates of this point are:

Problem : P (x, y) = (1, 3). Express it in polar coordinates (r, θ) two different ways such that 0≤ θ < 2 (r, θ) = (2, /3), (- 2, 4 /3). Problem : P(x, y) = (-4, 0). Express it in polar coordinates (r, θ) two different ways such that 0≤ θ < 2. (r, θ) = (4, ), (- 4, 0). Problem : P (x, y) = (-7, -7), express it in polar coordinates (r, θ) two different ways such that 0≤ θ < 2. (r, θ) = ( 98, 5 /4), (- 98, /4). Problem : Given a point in polar coordinates (r, θ) = (3, /4), express it in rectangular coordinates (x, y) = (3√ 2/2, 3√ 2/2)

Problem : Transform the equation x 2 + y 2 + 5 x = 0 to polar coordinate form. x 2 + y 2 + 5 x = 0 r 2 + 5(r cos θ) = 0 r ( r + 5 cos θ) = 0 The equation r = 0 is the pole. Thus, keep only the other equation: r + 5 cos θ = 0 Problem : Transform the equation r = 4 sin θ to Cartesian coordinate form. What is the graph? Describe it fully!!!

Problem : What is the maximum value of | r| for the following polar equations: a) r = cos(2 θ) θ = n /2 where n is an integer and | r| = 1 b) r = 3 + sin(θ) θ = /2+2 n where n is an integer and | r| = 4 c) r = 2 cos(θ) - 1 θ = (2 n + 1) where n is an integer and | r| = 3 Problem : Find the intercepts and zeroes of the following polar equations: a) r = cos(θ) + 1 • Polar axis intercepts: (r, θ) = (2, 2 n ), (0, (2 n + 1) ) , where n is an integer. • Line θ = /2 intercepts: (r, θ) = (1, /2 + n ) , where n is an integer. r = cos(θ) + 1 = 0 for θ = (2 n + 1) , where n is an integer b) r = 4 sin(θ) • Polar axis intercepts: (r, θ) = (0, n ) where n is an integer. • Line θ = /2 intercepts: (r, θ) = (4, /2 +2 n ) where n is an integer. r = 4 sin(θ) = 0 for θ = n , where n is an integer.

TI – 84 plus Graphing polar equations example: graph the polar equation r = 1 - sinθ 1. Hit the MODE key. 2. Arrow down to where it says Func and then use the right arrow to choose Pol. 3. Hit ENTER The calculator is now in parametric equations mode. 4. Hit the Y= key. 5. In the r 1 slot, type r = 1 - sin(θ) Hit X, T, θ, n key for typing θ • Press [WINDOW] and enter the following settings: θmin = 0 θmax = 2π With these settings the calculator will evaluate the θstep = π /24 function from θ = 0 to θ = 2 π in increments of π /24. Xmin = -3 • Press [GRAPH]. Xmax = 3 Xscl = 1 Ymin = -3 Ymax = 1 Yscl = 1

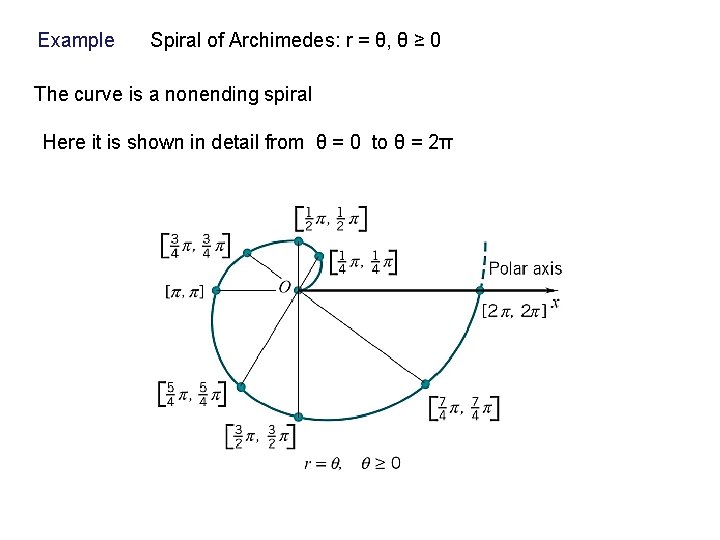
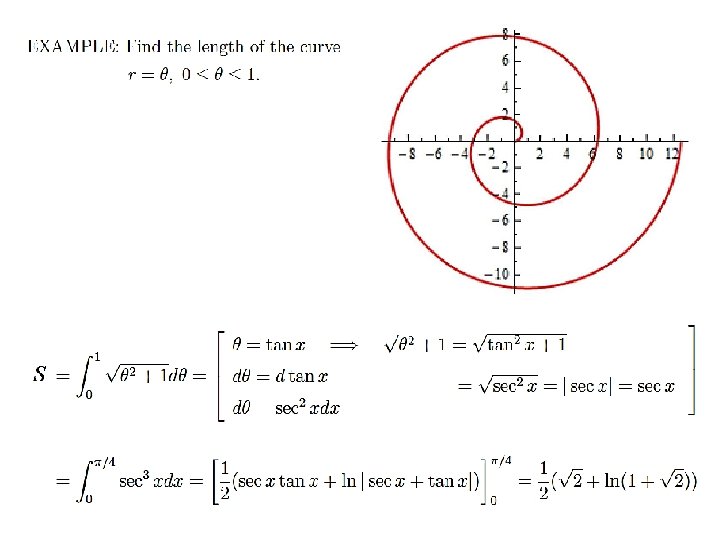
Example Spiral of Archimedes: r = θ, θ ≥ 0 The curve is a nonending spiral Here it is shown in detail from θ = 0 to θ = 2π

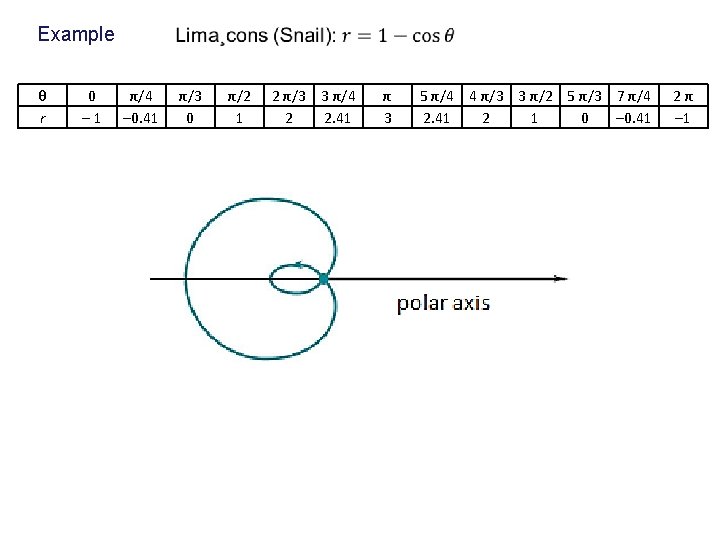
Example θ r 0 – 1 π/4 – 0. 41 π/3 0 π/2 1 2 π/3 3 π/4 2 2. 41 π 3 5 π/4 4 π/3 3 π/2 5 π/3 7 π/4 2. 41 2 1 0 – 0. 41 2π – 1

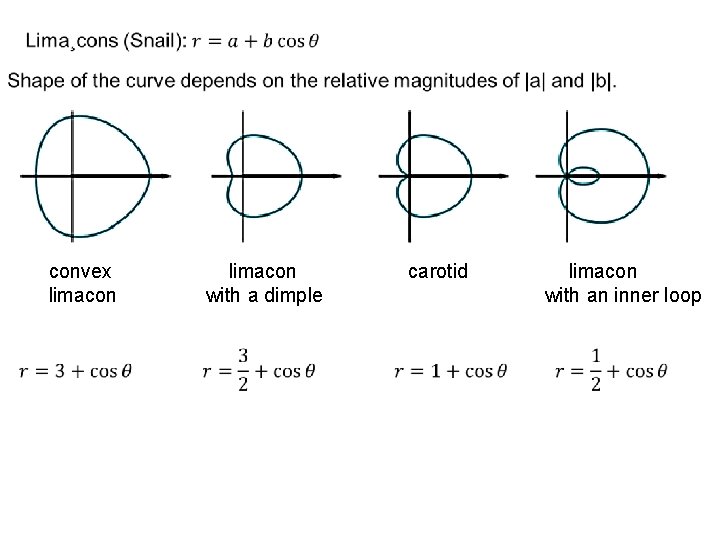
convex limacon carotid limacon with a dimple with an inner loop
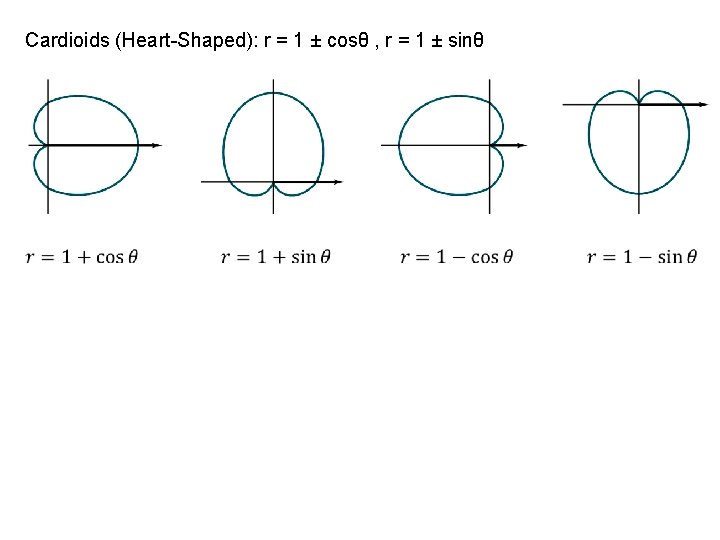
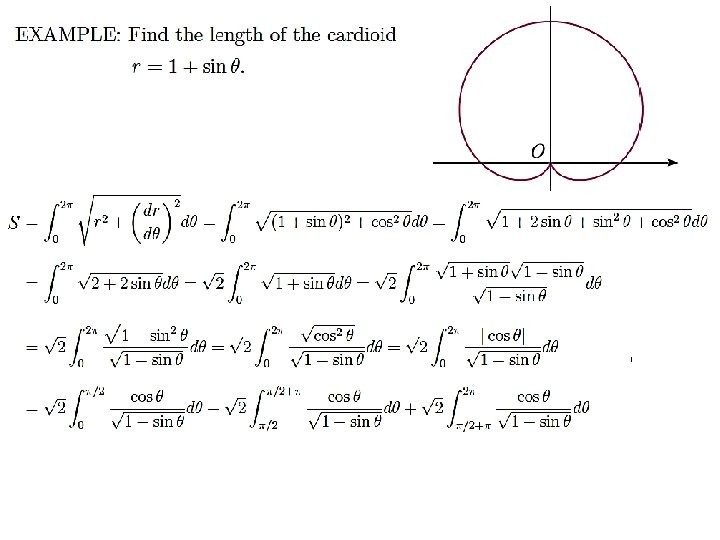
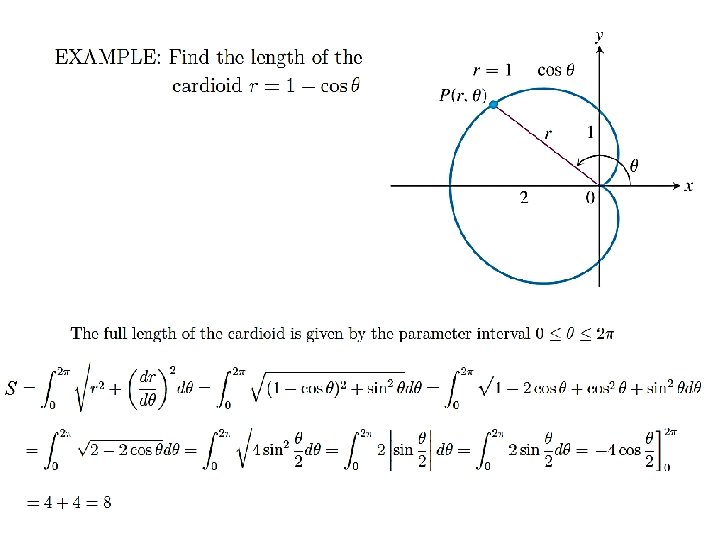
Cardioids (Heart-Shaped): r = 1 ± cosθ , r = 1 ± sinθ

Flowers Petal Curve: r = cos 2 θ

Petal Curves: r = a cos n θ, r = a sin n θ r = sin 3θ r = cos 4 θ • If n is odd, there are n petals. • If n is even, there are 2 n petals.

Tests for Symmetry: x-axis: If (r, ) is on the graph, so is (r, - ).

Tests for Symmetry: y-axis: If (r, ) is on the graph, so is (r, - ) or (-r, - ).

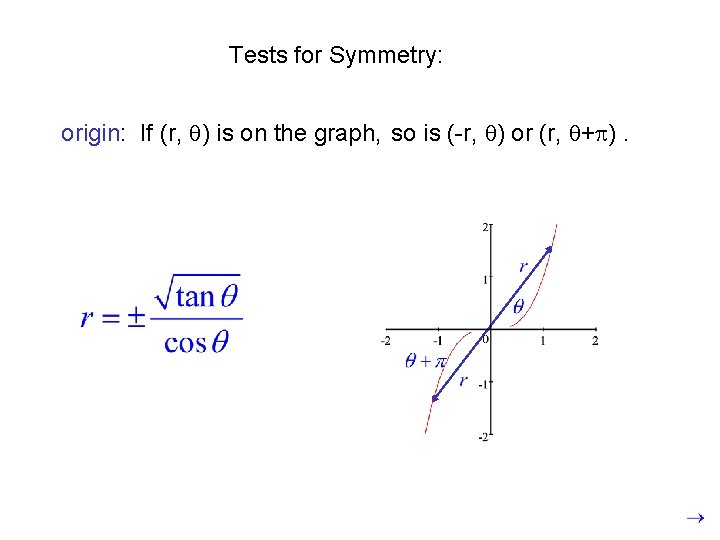
Tests for Symmetry: origin: If (r, ) is on the graph, so is (-r, ) or (r, + ).

Tests for Symmetry: If a graph has two symmetries, then it has all three:

Try graphing this on the TI-89.

First and second derivative of r = r( ): and now good luck Note that rather than trying to remember this formula it would probably be easier to remember how we derived it.

Example: Find the slope of a polar curve:




Area Inside a Polar Graph: For a very small , the curve could be approximated by a straight line and the area could be found using the triangle formula: 1 ≤ ≤ 2

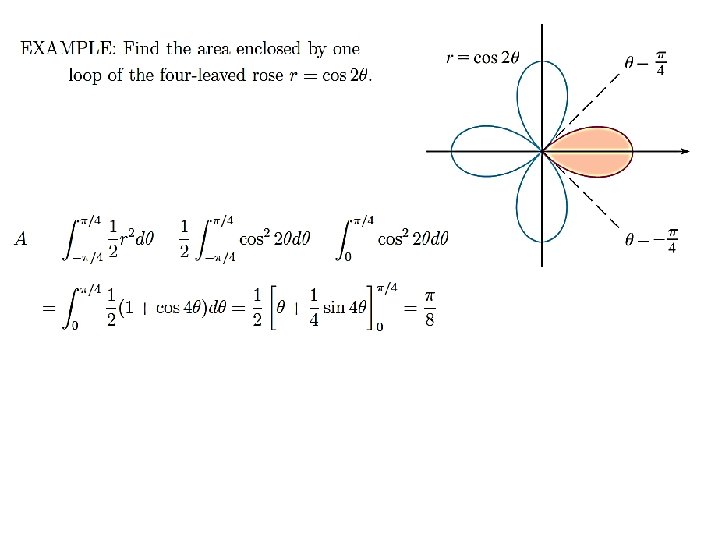
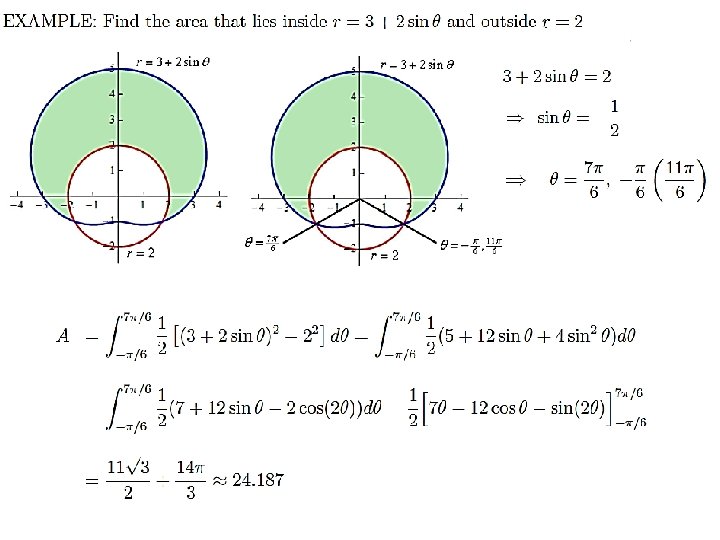
Example: Find the area enclosed by:

example: Find the area of the inner loop of r = 2 + 4 cos θ






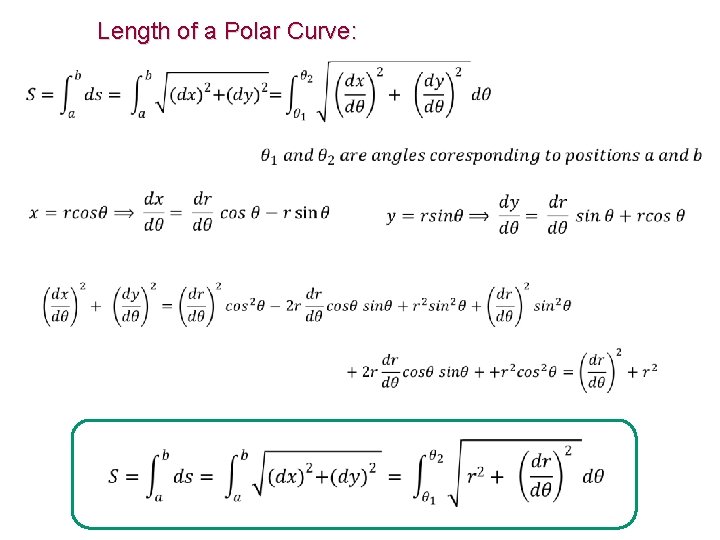
Length of a Polar Curve:




 Polar derivative
Polar derivative Homogeneous coordinates vs cartesian coordinates
Homogeneous coordinates vs cartesian coordinates Consecutive coordinates and independent coordinates
Consecutive coordinates and independent coordinates Polar coordinate symmetry
Polar coordinate symmetry Polar coordinates in real life
Polar coordinates in real life Calculator art project
Calculator art project Rectangular vs polar coordinates
Rectangular vs polar coordinates Polar coordinates dynamics examples
Polar coordinates dynamics examples Polar to rectangular equation
Polar to rectangular equation Y=rsin
Y=rsin Multiple representations of polar coordinates
Multiple representations of polar coordinates Polar coordinates
Polar coordinates Polar integrals
Polar integrals Parametric equations and polar coordinates
Parametric equations and polar coordinates Pole in polar coordinates
Pole in polar coordinates How to find polar coordinates
How to find polar coordinates Area between curves formula
Area between curves formula Conic sections in polar coordinates
Conic sections in polar coordinates Geodesic polar coordinates
Geodesic polar coordinates Laplace equation in spherical polar coordinates
Laplace equation in spherical polar coordinates How to graph polar coordinates on ti-84
How to graph polar coordinates on ti-84 Pole polar coordinates
Pole polar coordinates Polar coordinates
Polar coordinates Kekontinuan fungsi
Kekontinuan fungsi Polar fft
Polar fft Conic section in polar coordinates
Conic section in polar coordinates In unidirectional system the dimensions are placed
In unidirectional system the dimensions are placed Kobe station rice
Kobe station rice Aims of education by kothari commission
Aims of education by kothari commission Write recommendation of yashpal committee
Write recommendation of yashpal committee Explain when rtv and anaerobic sealers are recommended.
Explain when rtv and anaerobic sealers are recommended. Journalistic na pagsulat katangian
Journalistic na pagsulat katangian Defects of curriculum
Defects of curriculum Recommended approach
Recommended approach Trip advisor namibia
Trip advisor namibia Amadeus ticket changer
Amadeus ticket changer 2015 nehrp recommended seismic provisions
2015 nehrp recommended seismic provisions Sae j 3061
Sae j 3061 Herold merisier
Herold merisier Recommended
Recommended