Similar Polygons SIMILAR POLYGONS Similar polygons have the






- Slides: 22

Similar Polygons

SIMILAR POLYGONS • Similar polygons have the same shape but not necessarily the same size. • Two polygons are similar if and only if their corresponding side lengths are proportional • The ratio of the lengths of the corresponding sides is called the scale factor. • The similar “symbol” is ~

Warm-Up 3. A model train engine is 9 centimeters long. The actual engine is 18 meters long. What is the scale of the model? ANSWER 1 cm : 2 m

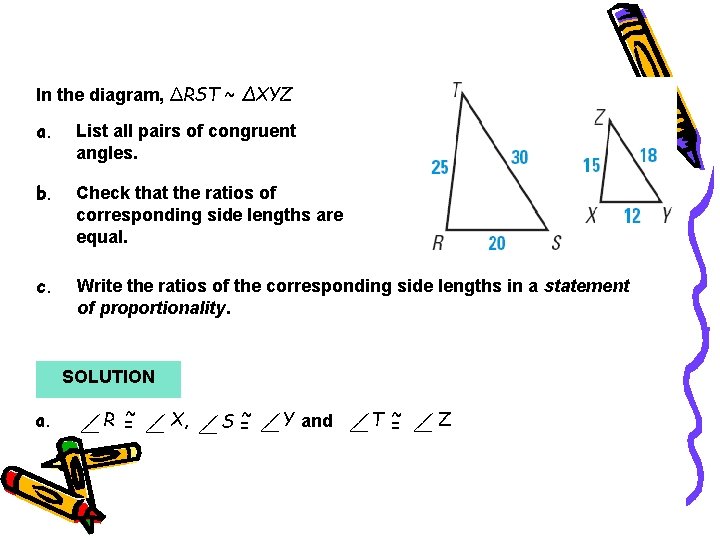
Example 1 In the diagram, ∆RST ~ ∆XYZ a. List all pairs of congruent angles. b. Check that the ratios of corresponding side lengths are equal. c. Write the ratios of the corresponding side lengths in a statement of proportionality. SOLUTION a. R =~ X, S =~ Y and T ~ = Z

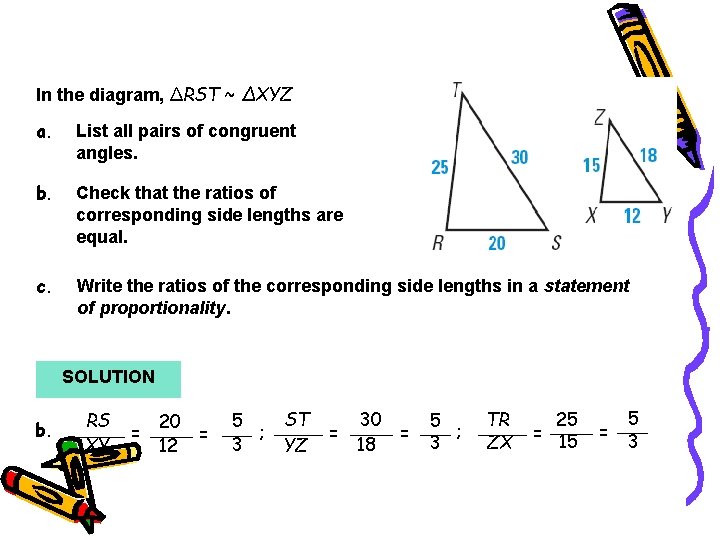
Example 1 In the diagram, ∆RST ~ ∆XYZ a. List all pairs of congruent angles. b. Check that the ratios of corresponding side lengths are equal. c. Write the ratios of the corresponding side lengths in a statement of proportionality. SOLUTION b. RS XY = 20 12 = 5 ; 3 ST YZ = 30 18 = 5 ; 3 TR ZX = 25 15 = 5 3

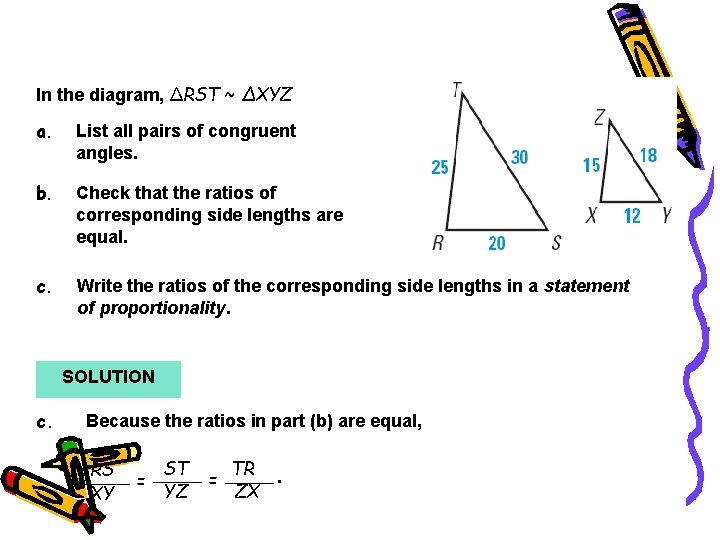
Example 1 In the diagram, ∆RST ~ ∆XYZ a. List all pairs of congruent angles. b. Check that the ratios of corresponding side lengths are equal. c. Write the ratios of the corresponding side lengths in a statement of proportionality. SOLUTION c. Because the ratios in part (b) are equal, RS XY = ST YZ = TR. ZX

Guided Practice 1. Given ∆ JKL ~ ∆ PQR, list all pairs of congruent angles. Write the ratios of the corresponding side lengths in a statement of proportionality. ANSWER ~ J = P, ~ K = Q and L ~ = R ; JK PQ = LJ KL = RP QR

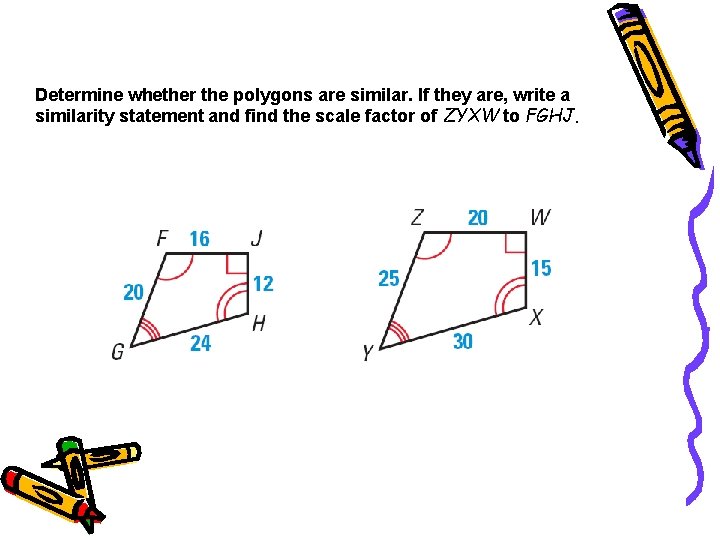
Example 2 Determine whether the polygons are similar. If they are, write a similarity statement and find the scale factor of ZYXW to FGHJ.

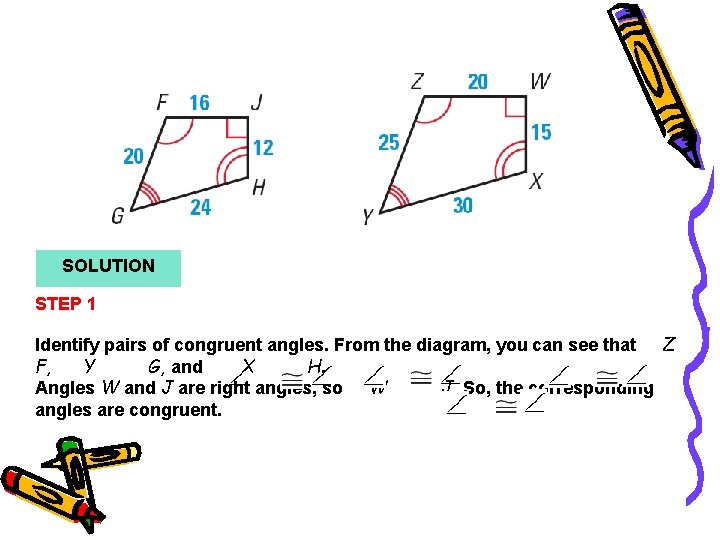
Example 2 SOLUTION STEP 1 Identify pairs of congruent angles. From the diagram, you can see that Z F, Y G, and X H. Angles W and J are right angles, so W J. So, the corresponding angles are congruent.

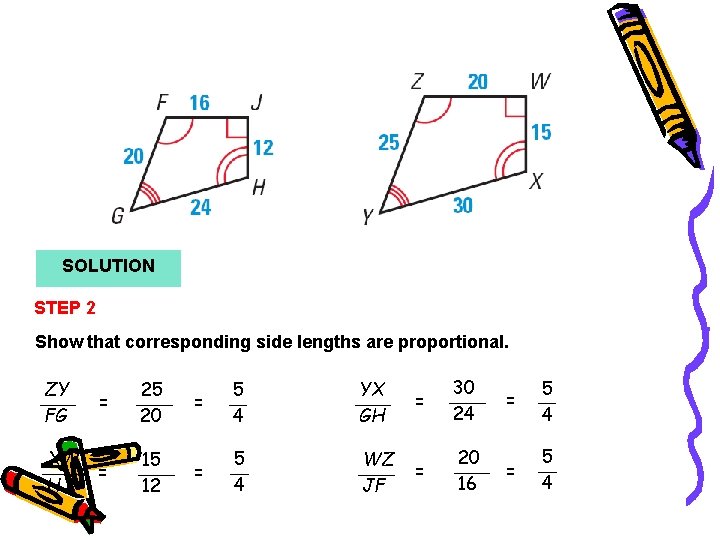
Example 2 SOLUTION STEP 2 Show that corresponding side lengths are proportional. ZY FG XW HJ = 25 20 = 15 12 = 5 4 YX GH = 5 4 WZ JF = 30 24 = 20 16 = 5 4

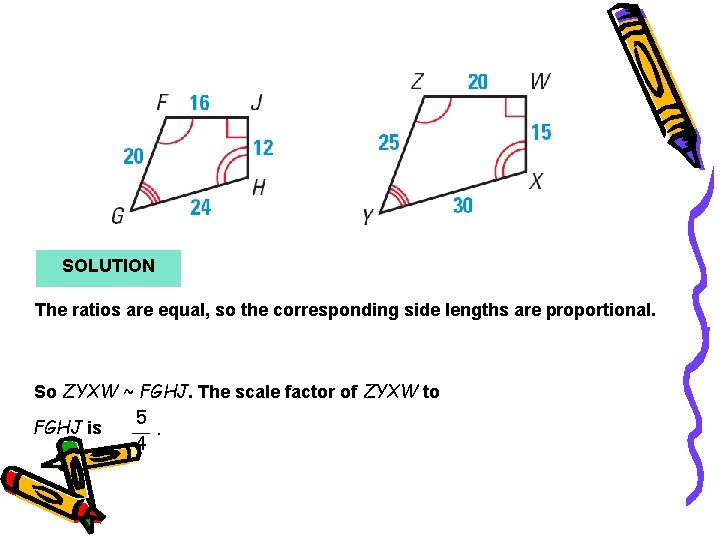
Example 2 SOLUTION The ratios are equal, so the corresponding side lengths are proportional. So ZYXW ~ FGHJ. The scale factor of ZYXW to 5 FGHJ is. 4

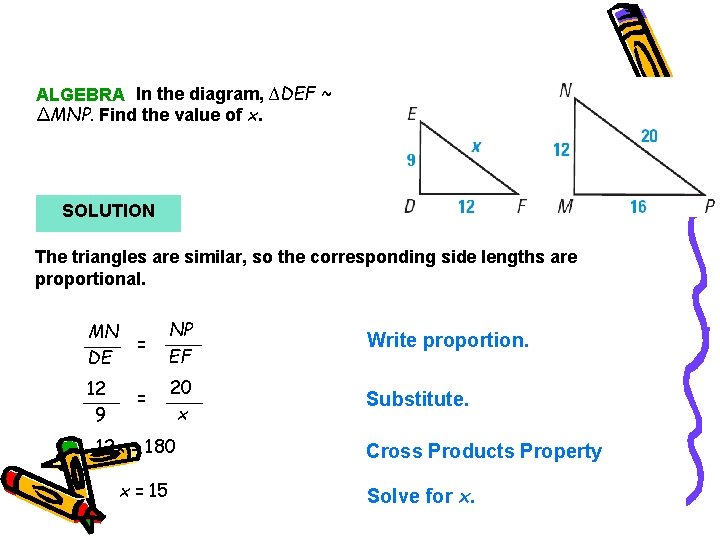
Example 3 ALGEBRA In the diagram, ∆DEF ~ ∆MNP. Find the value of x. SOLUTION The triangles are similar, so the corresponding side lengths are proportional. MN DE = NP EF Write proportion. 12 9 = 20 x Substitute. 12 x = 180 x = 15 Cross Products Property Solve for x.

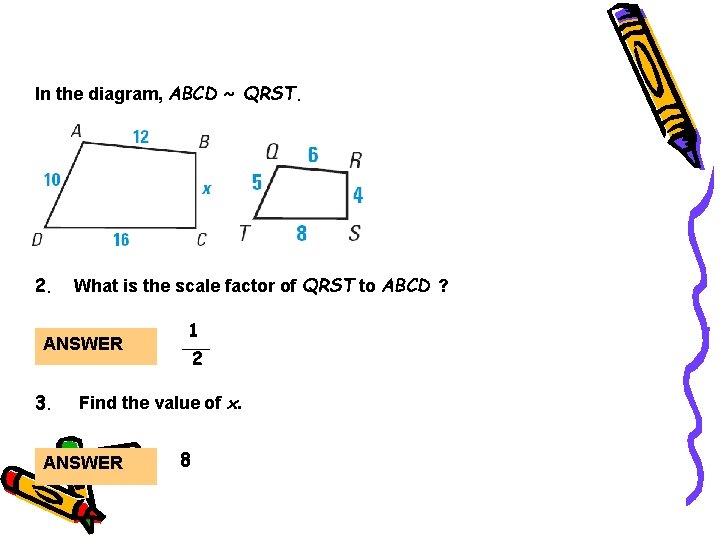
Guided Practice In the diagram, ABCD ~ QRST. 2. What is the scale factor of QRST to ABCD ? ANSWER 3. 1 2 Find the value of x. ANSWER 8

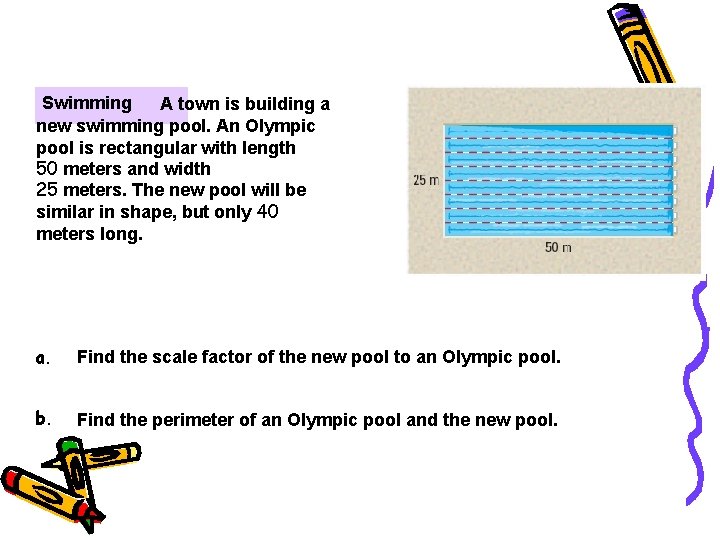
Example 4 Swimming A town is building a new swimming pool. An Olympic pool is rectangular with length 50 meters and width 25 meters. The new pool will be similar in shape, but only 40 meters long. a. Find the scale factor of the new pool to an Olympic pool. b. Find the perimeter of an Olympic pool and the new pool.

Example 4 SOLUTION a. Because the new pool will be similar to an Olympic pool, the scale factor is the ratio of the lengths, 40 50 b. = 4. 5 The perimeter of an Olympic pool is 2(50) + 2(25) = 150 meters. You can use Theorem 6. 1 to find the perimeter x of the new pool. x 150 = 4 5 x = 120 Use Theorem 6. 1 to write a proportion. Multiply each side by 150 and simplify. The perimeter of the new pool is 120 meters.

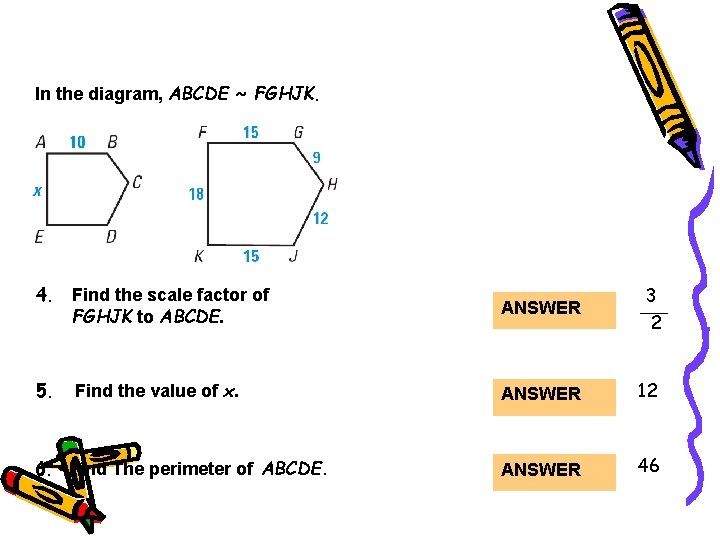
Guided Practice In the diagram, ABCDE ~ FGHJK. 4. Find the scale factor of FGHJK to ABCDE. ANSWER 5. ANSWER 12 ANSWER 46 Find the value of x. 6. Find The perimeter of ABCDE. 3 2

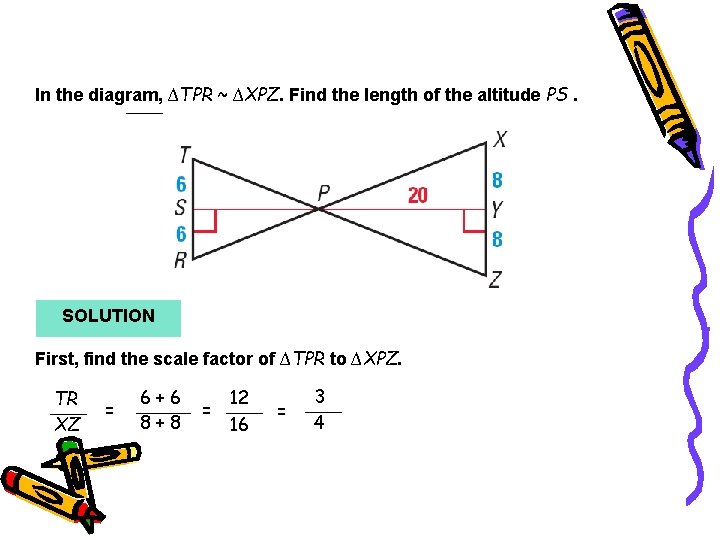
Example 5 In the diagram, ∆TPR ~ ∆XPZ. Find the length of the altitude PS. SOLUTION First, find the scale factor of ∆TPR to ∆XPZ. TR XZ = 6+6 8+8 = 12 16 = 3 4

Example 5 Because the ratio of the lengths of the altitudes in similar triangles is equal to the scale factor, you can write the following proportion. PS PY = 3 4 PS 20 = 3 4 PS = 15 Write proportion. Substitute 20 for PY. Multiply each side by 20 and simplify. The length of the altitude PS is 15.

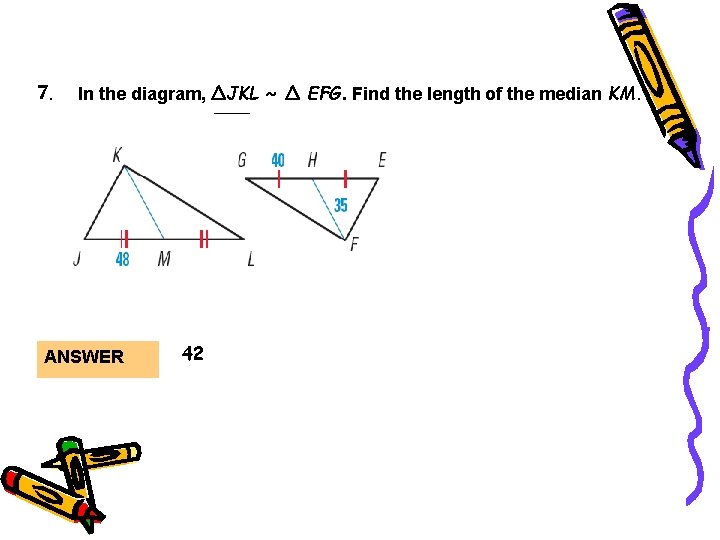
Guided Practice 7. In the diagram, ∆JKL ~ ∆ EFG. Find the length of the median KM. ANSWER 42

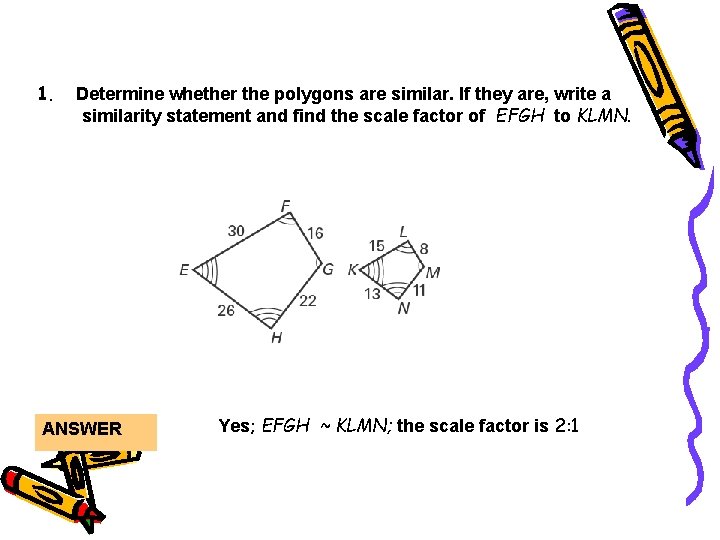
Lesson Quiz 1. Determine whether the polygons are similar. If they are, write a similarity statement and find the scale factor of EFGH to KLMN. ANSWER Yes; EFGH ~ KLMN; the scale factor is 2: 1

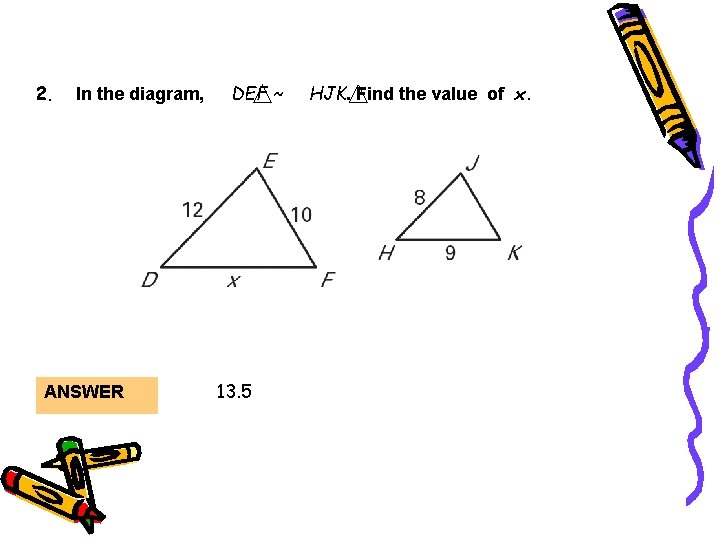
Lesson Quiz 2. In the diagram, ANSWER DEF ~ 13. 5 HJK. Find the value of x.

Lesson Quiz 3. Two similar triangles have the scale factor 5 : 4. Find the ratio of their corresponding altitudes and median. ANSWER 4. 5: 4; 5: 4 Two similar triangles have the scale factor 3 : 7. Find the ratio of their corresponding perimeters and areas. ANSWER 3 : 7; 9: 49