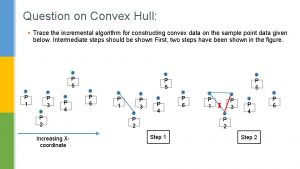
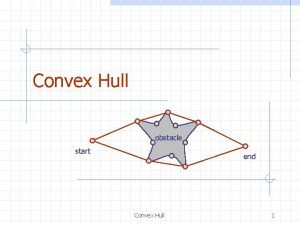
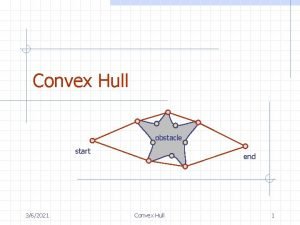
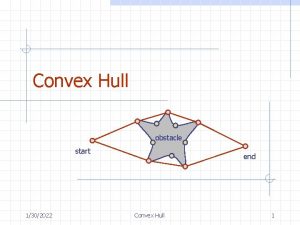
Convex hull smallest convex set containing all the



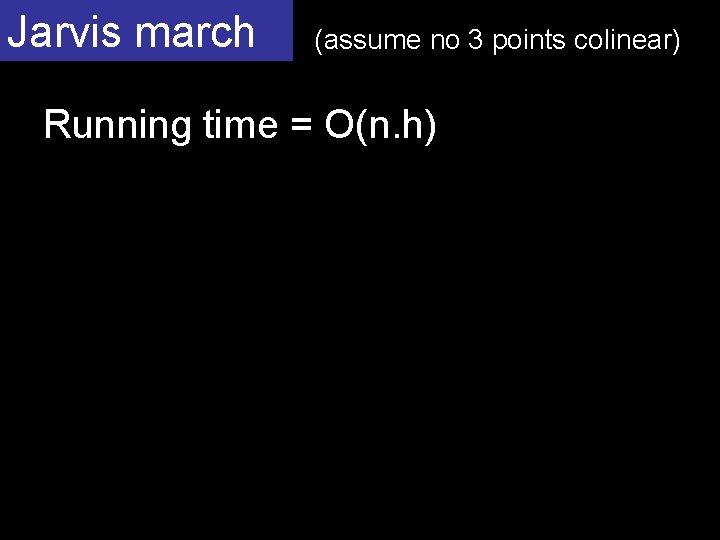
















- Slides: 39

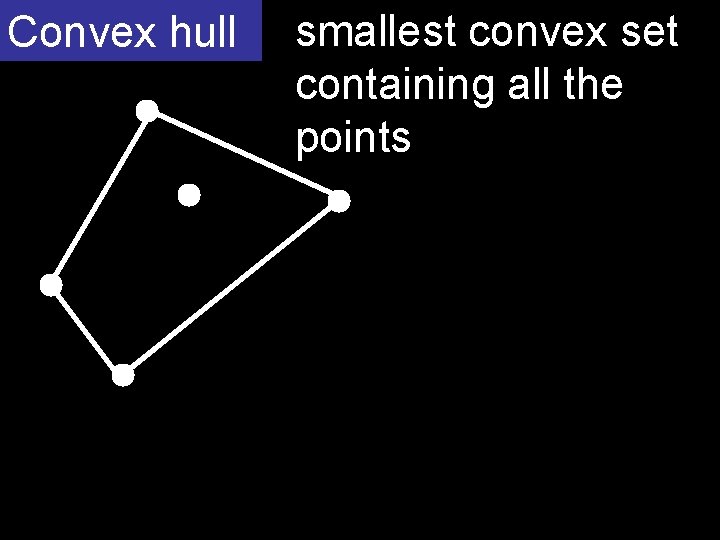
Convex hull smallest convex set containing all the points

Convex hull smallest convex set containing all the points

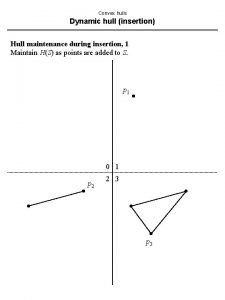
Convex hull 3 smallest convex set containing all the points 2 4 1 start = 1 1. next = 2 = 3. prev 2. next = 3 = 4. prev 3. next = 4 = 1. prev 4. next = 1 = 2. prev representation = circular doubly-linked list of points on the boundary of the convex hull

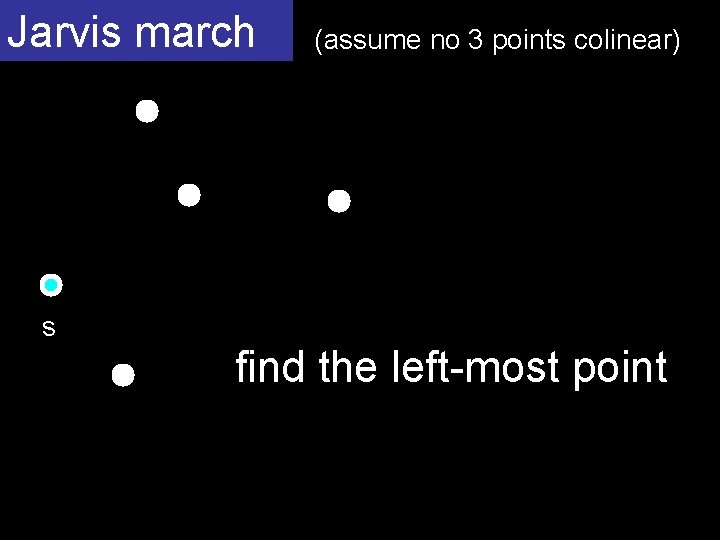
Jarvis march (assume no 3 points colinear) s find the left-most point

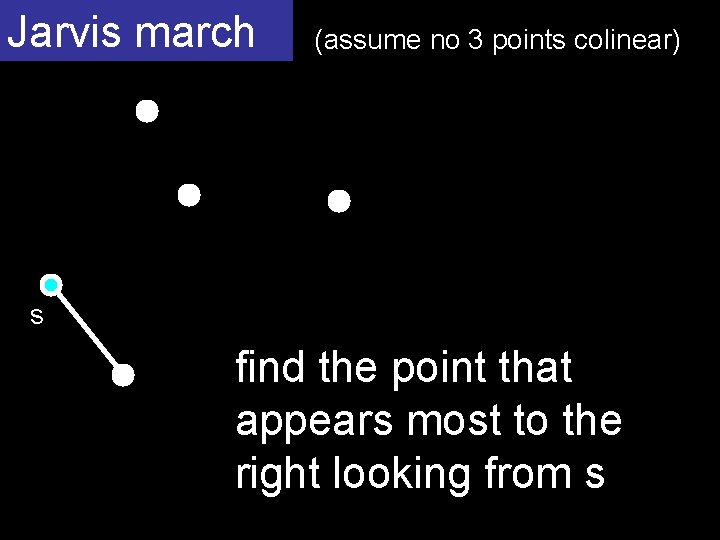
Jarvis march (assume no 3 points colinear) s find the point that appears most to the right looking from s

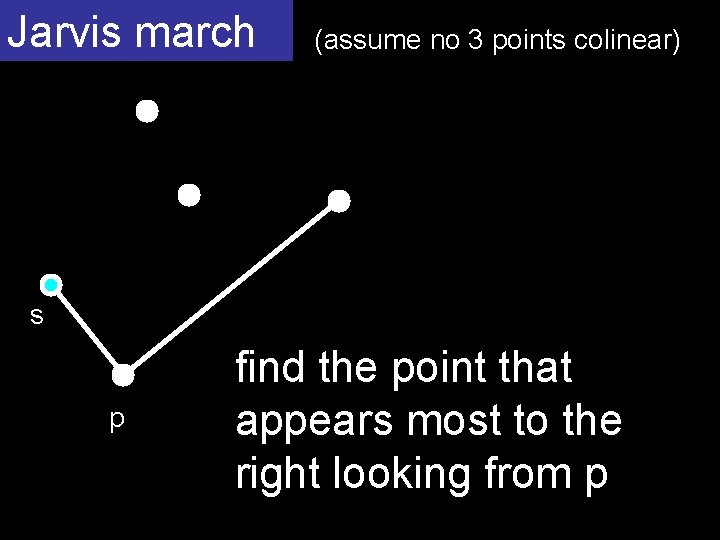
Jarvis march (assume no 3 points colinear) s p find the point that appears most to the right looking from p

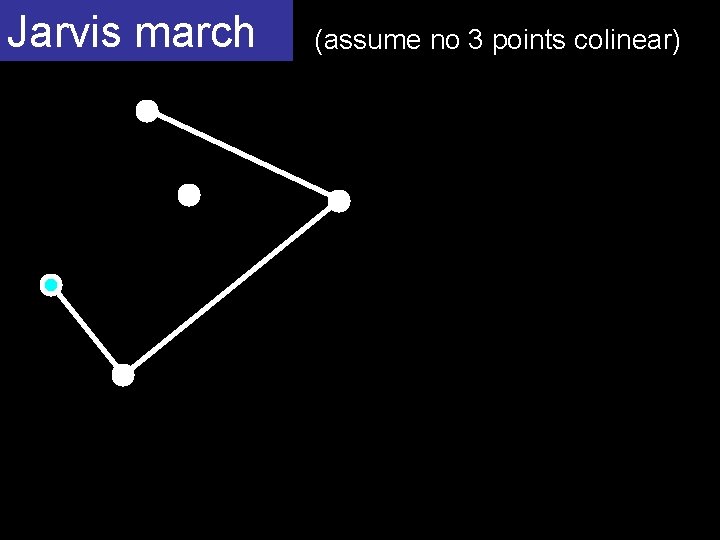
Jarvis march (assume no 3 points colinear)

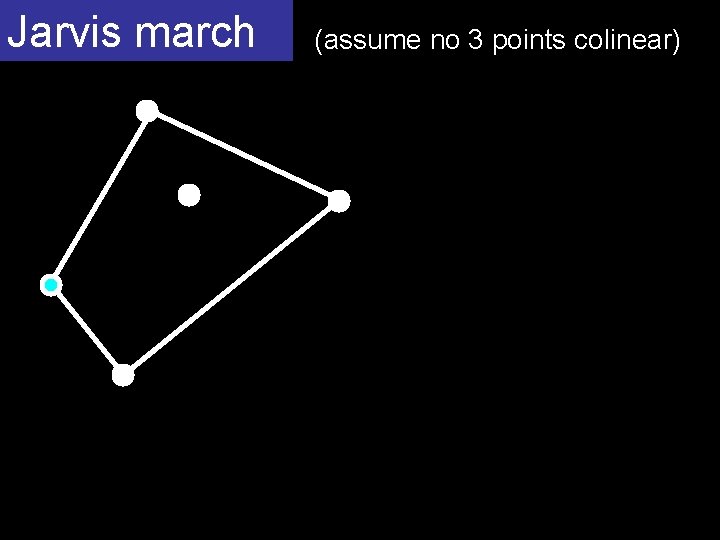
Jarvis march (assume no 3 points colinear)

Jarvis march (assume no 3 points colinear) s point with smallest x-coord p s repeat PRINT(p) q point other than p for i from 1 to n do if i p and point i to the right of line (p, q) then q i p q until p = s
Jarvis march (assume no 3 points colinear) Running time = O(n. h)

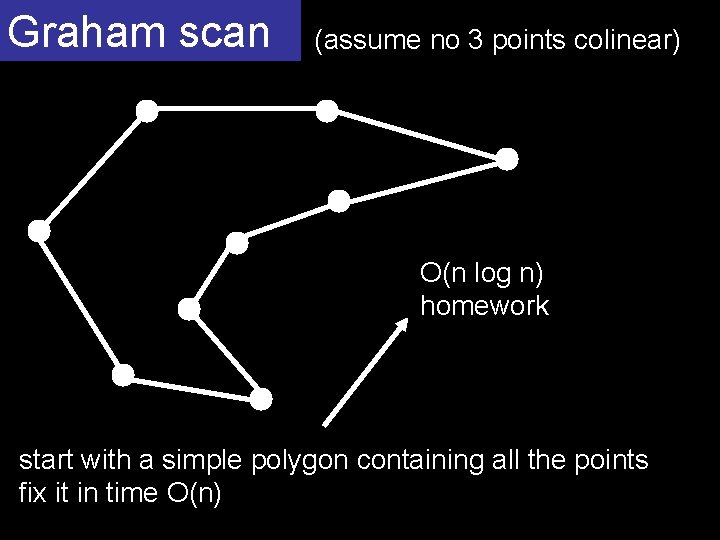
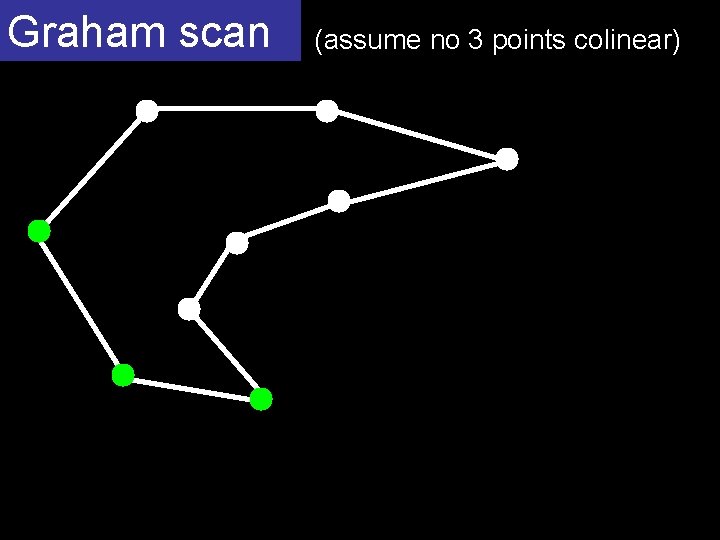
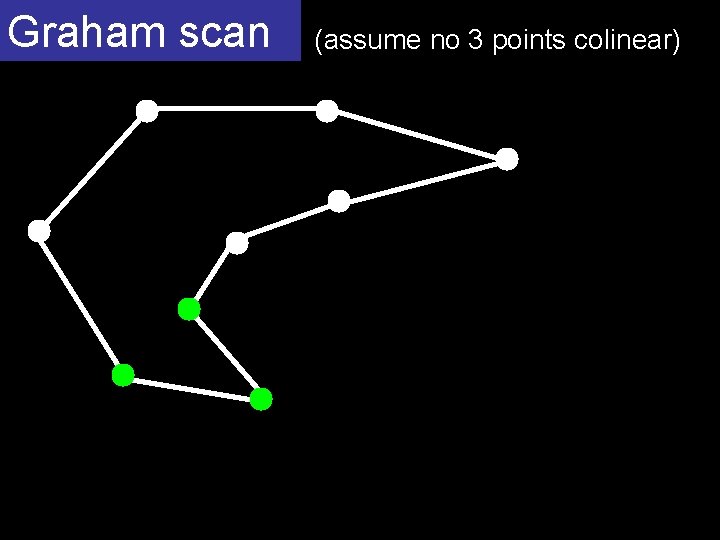
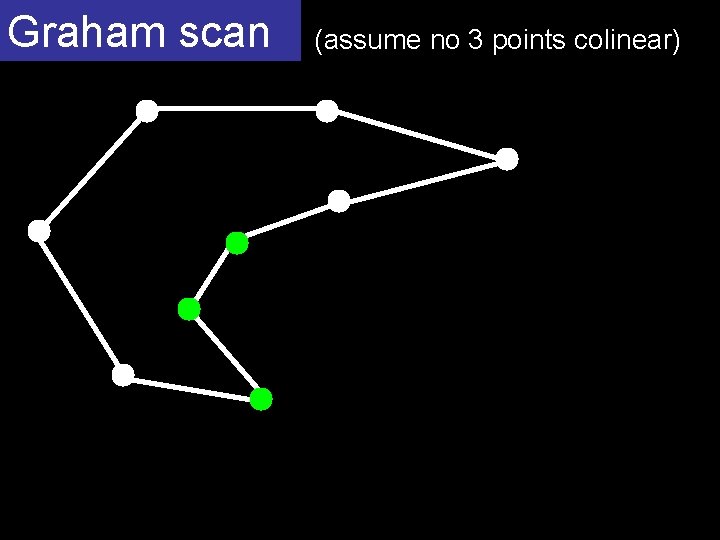
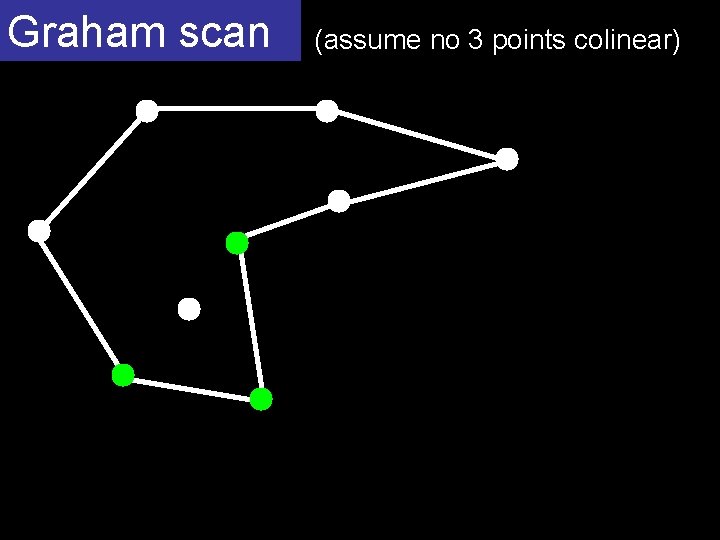
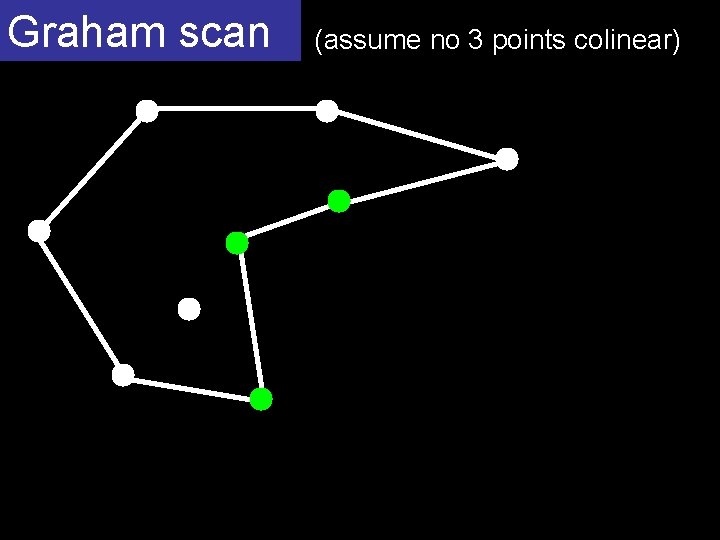
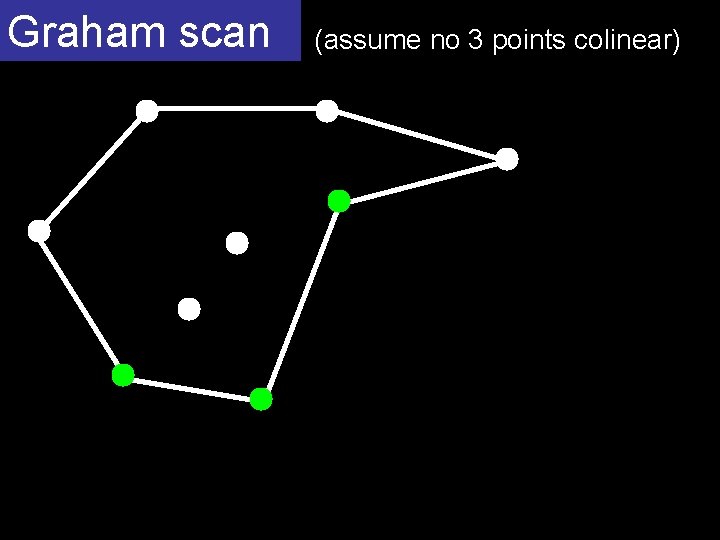
Graham scan (assume no 3 points colinear) O(n log n) homework start with a simple polygon containing all the points fix it in time O(n)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear)

Graham scan (assume no 3 points colinear) A start B next(A) C next(B) repeat 2 n times if C is to the right of AB then A. next C; C. prev A B A A prev(A) else A B B C C next(C)

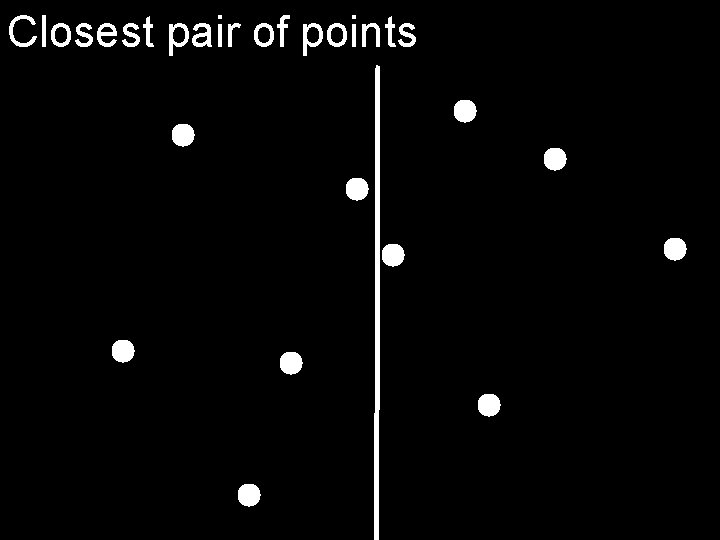
Closest pair of points

Closest pair of points

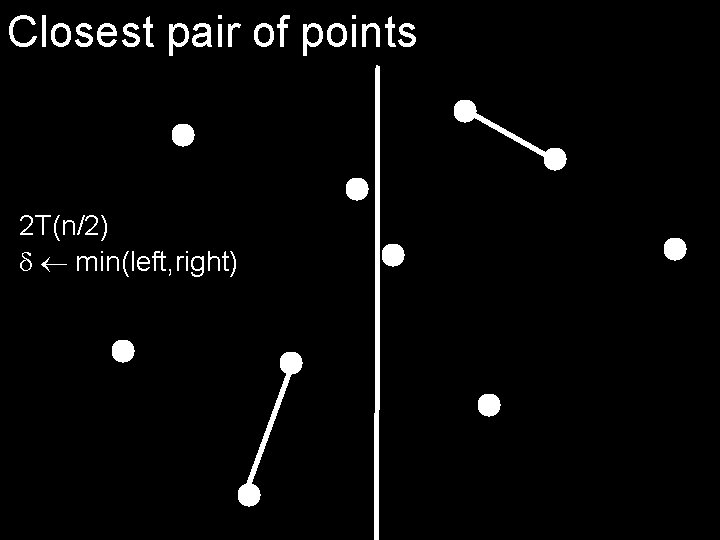
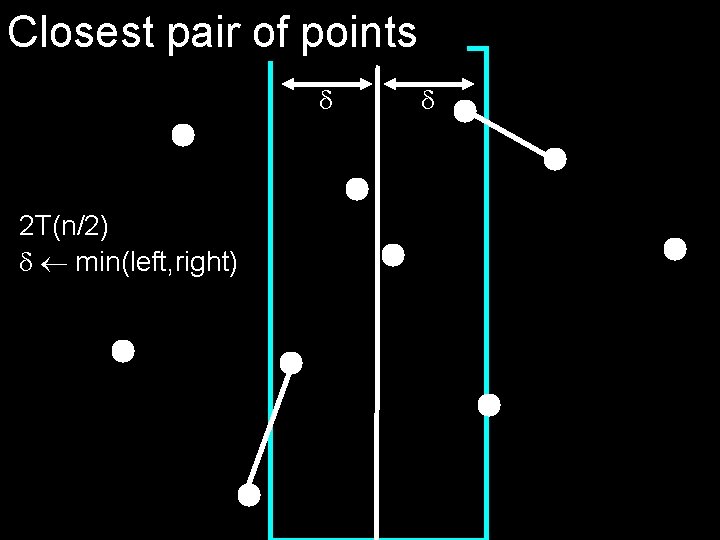
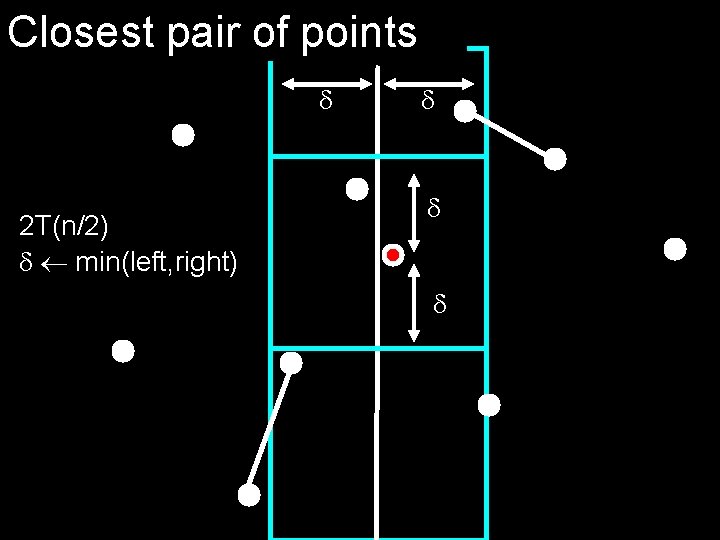
Closest pair of points 2 T(n/2) min(left, right)

Closest pair of points 2 T(n/2) min(left, right)

Closest pair of points 2 T(n/2) min(left, right)

Closest pair of points pre-processing X sort the points by x-coordinate Y sort the points by y-coordinate Closest-pair(S) if |S|=1 then return if |S|=2 then return the distance of the pair split S into S 1 and S 2 by the X-coord 1 Closest-pair(S 1), 2 Closest-pair(S 2) min( 1, 2) for points x in according to Y check 12 points around x, update if a closer pair found

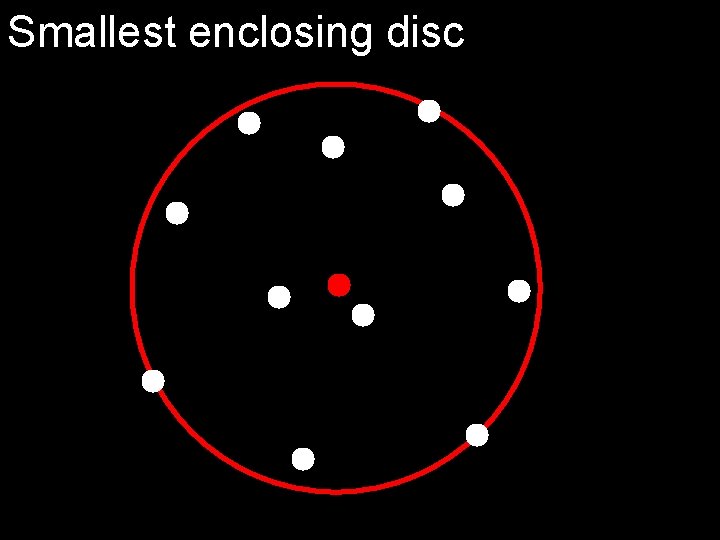
Smallest enclosing disc

Smallest enclosing disc

Smallest enclosing disc Claim #1: The smallest enclosing disc is unique.

Smallest enclosing disc Claim #1: The smallest enclosing disc is unique.

Smallest enclosing disc SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x)

Smallest enclosing disc SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) SED-with-point(S, y) pick a random point x S (c, r) SED-with-point(S-{x}, y) if x Disc(c, r) then return (c, r) else return SED-with-2 -points(S, y, x)

Smallest enclosing disc SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) SED-with-point(S, y) pick a random point x S (c, r) SED-with-point(S-{x}, y) if x Disc(c, r) then return (c, r) else return SED-with-2 -points(S, y, x) SED-with-2 -point(S, y, z) pick a random point x S (c, r) SED-with-2 -points(S-{x}, y, z) if x Disc(c, r) then return (c, r) else return circle given by x, y, z

Running time ? SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) SED-with-point(S, y) pick a random point x S (c, r) SED-with-point(S-{x}, y) if x Disc(c, r) then return (c, r) else return SED-with-2 -points(S, y, x) SED-with-2 -point(S, y, z) pick a random point x S (c, r) SED-with-2 -points(S-{x}, y, z) if x Disc(c, r) then return (c, r) else return circle given by x, y, z

Running time ? SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) SED-with-point(S, y) pick a random point x S (c, r) SED-with-point(S-{x}, y) if x Disc(c, r) then return (c, r) else return SED-with-2 -points(S, y, x) SED-with-2 -point(S, y, z) pick a random point x S (c, r) SED-with-2 -points(S-{x}, y, z) if x Disc(c, r) then return (c, r) else return circle given by x, y, z O(n)

Running time ? SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) SED-with-point(S, y) pick a random point x S (c, r) SED-with-point(S-{x}, y) if x Disc(c, r) then return (c, r) else return SED-with-2 -points(S, y, x) T(n) = T(n-1) + T(n) = O(n) 2 n SED-with-2 -points O(n)

Running time ? SED(S) pick a random point x S (c, r) SED(S-{x}) if x Disc(c, r) then return (c, r) else return SED-with-point(S, x) T(n) = T(n-1) + T(n) = O(n) 2 n SED-with-point O(n)

Smallest enclosing disc md(I, B) = smallest enclosing disc with B on the boundary and I inside Claim #2: if x is inside md(I, B) then md(I {x}, B) = md(I, B)

Smallest enclosing disc md(I, B) = smallest enclosing disc with B on the boundary and I inside Claim #3: if x is outside of md(I, B) then md(I {x}, B) = md(I, B {x})

Smallest enclosing disc md(I, B) = smallest enclosing disc with B on the boundary and I inside Claim #3: if x is outside of md(I, B) then md(I {x}, B) = md(I, B {x}) x md(I, B) md(l {x}, B)

Smallest enclosing disc md(I, B) = smallest enclosing disc with B on the boundary and I inside Claim #3: if x is outside of md(I, B) then md(I {x}, B) = md(I, B {x}) Claim #2: if x is inside md(I, B) then md(I {x}, B) = md(I, B) Claim #1: md(I, B) is unique
 Convex hull is the smallest convex set
Convex hull is the smallest convex set Kanat tangwongsan
Kanat tangwongsan Concave vs convex polygon
Concave vs convex polygon Convex hull collision detection
Convex hull collision detection Incremental convex hull algorithm
Incremental convex hull algorithm Convex hull
Convex hull Concave vs convex shapes
Concave vs convex shapes Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
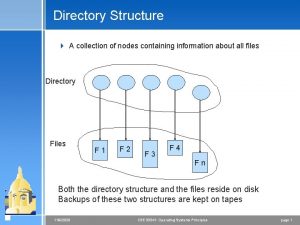
Training set validation set test set Collection of nodes containing information about all files
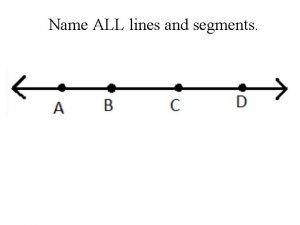
Collection of nodes containing information about all files Name 3 points
Name 3 points What is the smallest living unit in the body
What is the smallest living unit in the body Bounded set vs centered set
Bounded set vs centered set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set What is the overlap of data set 1 and data set 2?
What is the overlap of data set 1 and data set 2? Surjective vs injective
Surjective vs injective Uscg mic codes
Uscg mic codes Jane dee hull elementary
Jane dee hull elementary Andy keels
Andy keels Myepad
Myepad Bet relate thin heifer
Bet relate thin heifer Vehicle hull identification number
Vehicle hull identification number Advantage and disadvantage of transverse framing
Advantage and disadvantage of transverse framing Hull and propeller performance
Hull and propeller performance Hull drive reduction theory
Hull drive reduction theory Apprendimento per associazionismo
Apprendimento per associazionismo Clark l. hull
Clark l. hull Bullet bond
Bullet bond Dorure circuits imprimés
Dorure circuits imprimés Coast guard hull identification number
Coast guard hull identification number For hull, drive reduction is ____.
For hull, drive reduction is ____. Clark leonard hull teoria
Clark leonard hull teoria How pin-up hits depot lease meaning
How pin-up hits depot lease meaning Corn minus the hull and germ.
Corn minus the hull and germ. Difference between o type and m type tubes
Difference between o type and m type tubes Sarkadi édes ősz
Sarkadi édes ősz Wheat germ is the whole grain minus the husk.
Wheat germ is the whole grain minus the husk. Apply for secondary school hull
Apply for secondary school hull