Convex hulls Dynamic hull insertion Hull maintenance during

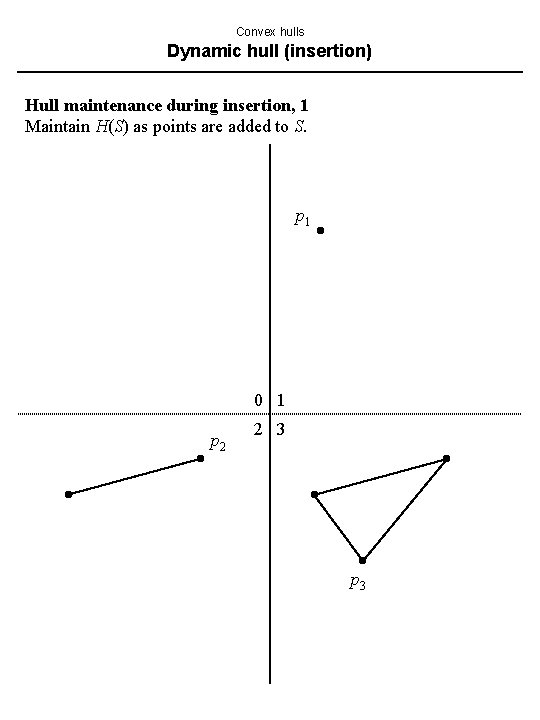
Convex hulls Dynamic hull (insertion) Hull maintenance during insertion, 1 Maintain H(S) as points are added to S. p 1 0 1 p 2 2 3 p 3

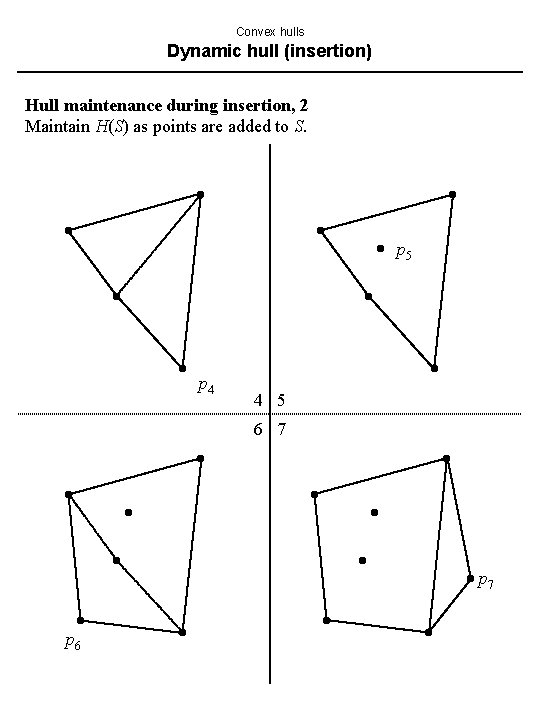
Convex hulls Dynamic hull (insertion) Hull maintenance during insertion, 2 Maintain H(S) as points are added to S. p 5 p 4 4 5 6 7 p 6

Convex hulls Dynamic hull (insertion) Definitions Preparata static Set of object remains fixed between operations (e. g. , between queries in repetitive mode). dynamic Set of objects can change between operations. Insertions and deletions allowed in general, but sometimes constrained. Implies S must be in some updatable data structure. on-line Algorithm cannot look ahead at input. off-line “Algorithm operates on all data collectively. ” Static or batched dynamic. real-time Updates must be completed during fixed interarrival time (often O(log N)). Edelsbrunner static Set of objects remains fixed between operations. dynamic Set of objects can change between operations. on-line Sequence of operations (insertions, deletions, queries) not known in advance, algorithm cannot look ahead. off-line Insertions and deletions contrained to come from a prespecified and usually small set. batched Sequence of operations fully known in advance, algorithm can look ahead. Chiang, Y. -J. and Tomassia, R. (1992). “Dynamic Algorithms in Computational Geometry”, Proceedings of the IEEE, Vol. 80, No. 9, September 1992, pp. 1412 -1434.

Convex hulls Dynamic hull (insertion) Problem definitions ON-LINE CONVEX HULL INSTANCE: Sequence of N points in the plane p 1, p 2, …, p. N. QUESTION: Find their convex hull in such a way that after pi is processed we have H({p 1, p 2, …, pi}). REAL-TIME CONVEX HULL INSTANCE: Sequence of N points in the plane p 1, p 2, …, p. N. QUESTION: Find their convex hull on-line assuming constant interarrival delay. The algorithm must maintain some representation of the hull and update it as points are inserted. Can this be done and still achieve O(N log N) time for the entire sequence? These are dynamic problems, but note that both of these problems are constrained to insertions only. Generalizing, we have: DYNAMIC CONVEX HULL (HULL MAINTENANCE) INSTANCE: An initially empty set S and a sequence of N points in the plane p 1, p 2, …, p. N, each of which corresponds to either an insertion or deletion from S. (Only a previously inserted point can be deleted). QUESTION: Maintain the convex hull H(S). ON-LINE CONVEX HULL and REAL-TIME CONVEX HULL covered today, DYNAMIC CONVEX HULL covered Wednesday.

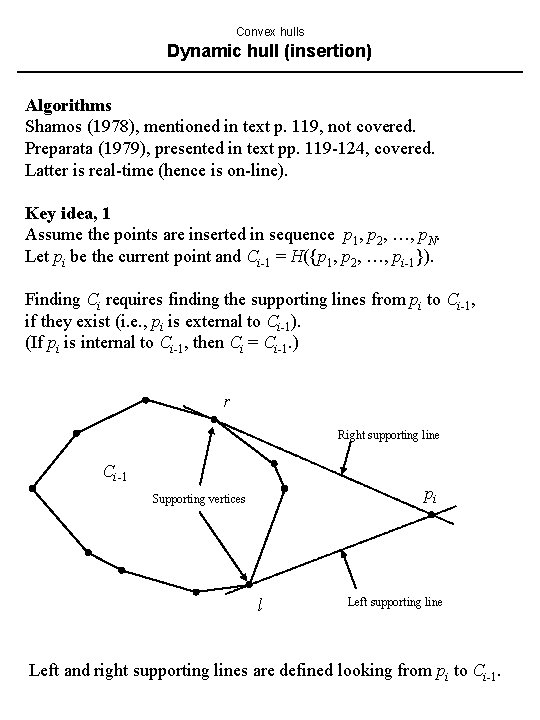
Convex hulls Dynamic hull (insertion) Algorithms Shamos (1978), mentioned in text p. 119, not covered. Preparata (1979), presented in text pp. 119 -124, covered. Latter is real-time (hence is on-line). Key idea, 1 Assume the points are inserted in sequence p 1, p 2, …, p. N. Let pi be the current point and Ci-1 = H({p 1, p 2, …, pi-1}). Finding Ci requires finding the supporting lines from pi to Ci-1, if they exist (i. e. , pi is external to Ci-1). (If pi is internal to Ci-1, then Ci = Ci-1. ) r Right supporting line Ci-1 pi Supporting vertices l Left supporting line Left and right supporting lines are defined looking from pi to Ci-1.

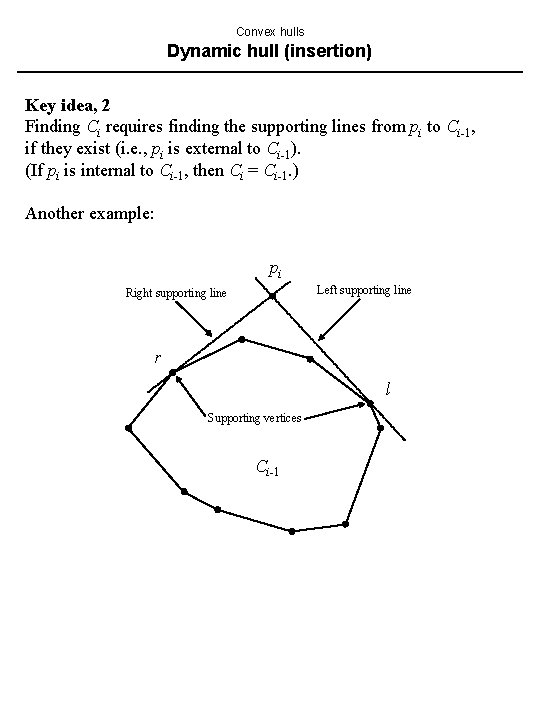
Convex hulls Dynamic hull (insertion) Key idea, 2 Finding Ci requires finding the supporting lines from pi to Ci-1, if they exist (i. e. , pi is external to Ci-1). (If pi is internal to Ci-1, then Ci = Ci-1. ) Another example: pi Left supporting line Right supporting line r l Supporting vertices Ci-1

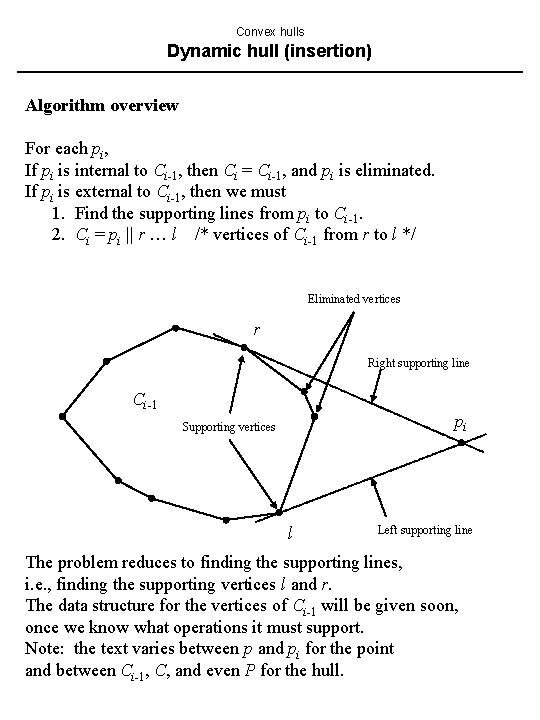
Convex hulls Dynamic hull (insertion) Algorithm overview For each pi, If pi is internal to Ci-1, then Ci = Ci-1, and pi is eliminated. If pi is external to Ci-1, then we must 1. Find the supporting lines from pi to Ci-1. 2. Ci = pi || r … l /* vertices of Ci-1 from r to l */ Eliminated vertices r Right supporting line Ci-1 pi Supporting vertices l Left supporting line The problem reduces to finding the supporting lines, i. e. , finding the supporting vertices l and r. The data structure for the vertices of Ci-1 will be given soon, once we know what operations it must support. Note: the text varies between p and pi for the point and between Ci-1, C, and even P for the hull.

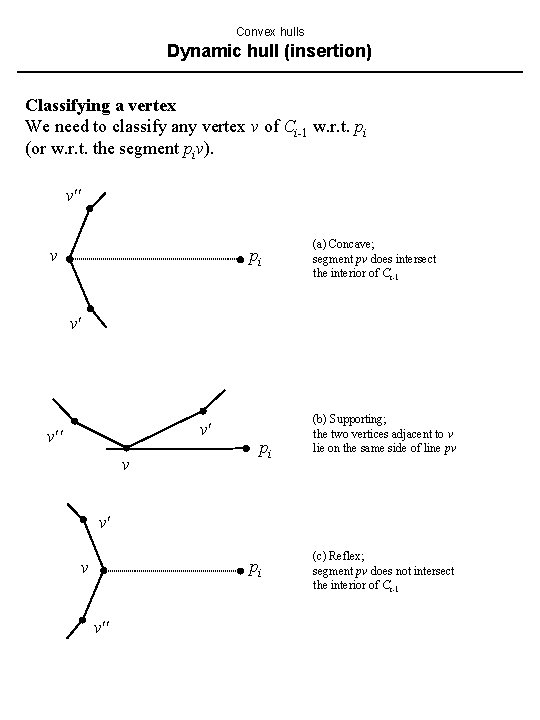
Convex hulls Dynamic hull (insertion) Classifying a vertex We need to classify any vertex v of Ci-1 w. r. t. pi (or w. r. t. the segment piv). v v pi (a) Concave; segment pv does intersect the interior of Ci-1 v v pi (b) Supporting; the two vertices adjacent to v lie on the same side of line pv v pi v v (c) Reflex; segment pv does not intersect the interior of Ci-1

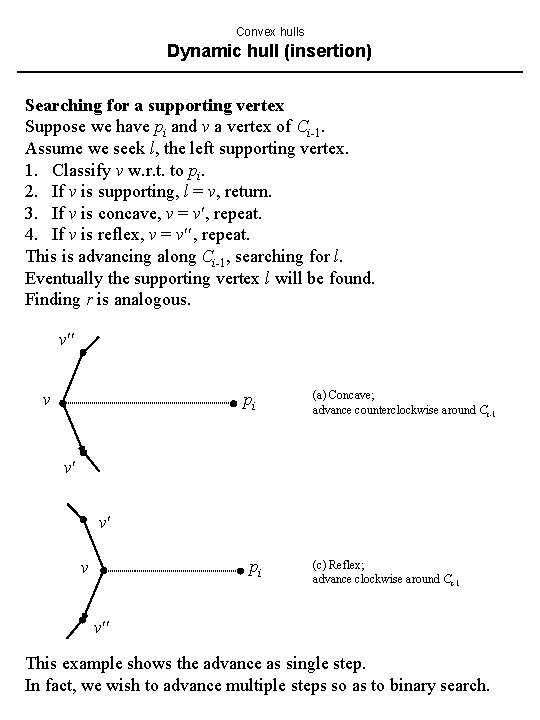
Convex hulls Dynamic hull (insertion) Searching for a supporting vertex Suppose we have pi and v a vertex of Ci-1. Assume we seek l, the left supporting vertex. 1. Classify v w. r. t. to pi. 2. If v is supporting, l = v, return. 3. If v is concave, v = v , repeat. 4. If v is reflex, v = v , repeat. This is advancing along Ci-1, searching for l. Eventually the supporting vertex l will be found. Finding r is analogous. v v pi (a) Concave; advance counterclockwise around Ci-1 v v pi v (c) Reflex; advance clockwise around Ci-1 v This example shows the advance as single step. In fact, we wish to advance multiple steps so as to binary search.

Convex hulls Dynamic hull (insertion) Data structure for Ci-1 The data structure for Ci-1 must support certain operations: 1. SEARCH an ordered string of items (the vertices of the hull) to locate the supporting lines from pi. 2. SPLIT a string of items into two substrings. 3. CONCATENATE (or SPLICE) two strings of items. 4. INSERT one item (e. g. , the current pi) in its ordered location. The concatenable queue data structure supports these operations, all in O(log N) time, where N is the number of items stored. (For more information, see [Aho, 1974] or [Reingold, 1977]. ) We assume the operations are available.

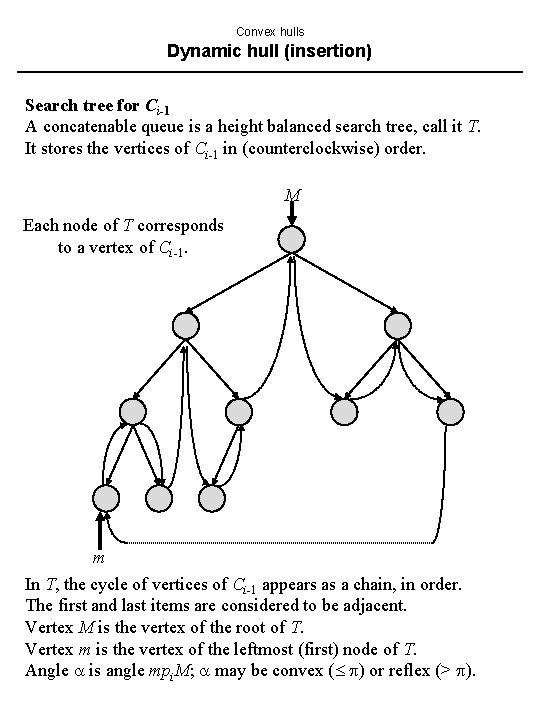
Convex hulls Dynamic hull (insertion) Search tree for Ci-1 A concatenable queue is a height balanced search tree, call it T. It stores the vertices of Ci-1 in (counterclockwise) order. M Each node of T corresponds to a vertex of Ci-1. m In T, the cycle of vertices of Ci-1 appears as a chain, in order. The first and last items are considered to be adjacent. Vertex M is the vertex of the root of T. Vertex m is the vertex of the leftmost (first) node of T. Angle is angle mpi. M; may be convex ( ) or reflex (> ).

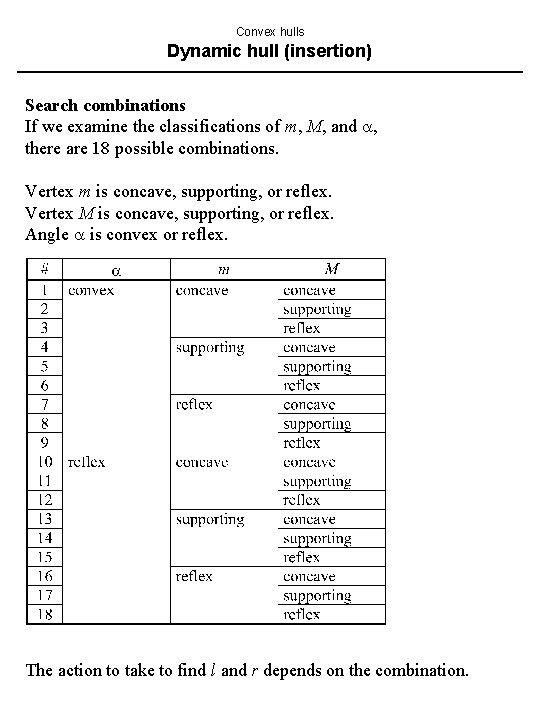
Convex hulls Dynamic hull (insertion) Search combinations If we examine the classifications of m, M, and , there are 18 possible combinations. Vertex m is concave, supporting, or reflex. Vertex M is concave, supporting, or reflex. Angle is convex or reflex. The action to take to find l and r depends on the combination.

Convex hulls Dynamic hull (insertion) Search cases The 18 possible combinations reduce to 8 cases where distinct actions are required. Figure 3. 16, text p. 122, illustrates the cases. In Figure 3. 16: The circle on which vertices m and M lie represents the convex hull Ci-1 (text says “polygon P”, p. 121). The ordered sequence of vertices starts at m and runs counterclockwise on the circle. L(M) and R(M) are the vertex sequences stored in the left and right subtrees of the root of tree T.

Convex hulls Dynamic hull (insertion) Finding l and r, 1 A distinct action is required to locate l and r in each of the 8 cases. Consider cases 2, 4, 6, and 8. Vertices l and r are known to exist, because pi cannot be internal. (Point pi can be internal only if m and M are both concave. ) In these cases, l and r are in separate subtrees of the root of T (one of the subtrees is extended to include the root in each case). Thus l and r can be found be analogous searches of the two subtrees. For example, l is found by the following function: 1 procedure LEFTSEARCH(T) 2 begin 3 c = ROOT(T) /* c is current vertex */ 4 if (line pic is supporting) 5 l=c 6 else 7 if (c is reflex) 8 T = LTREE(c) /* Root of left subtree */ 9 else /* c is concave */ 10 T = RTREE(c) /* Root of right subtree */ 11 endif 12 l = LEFTSEARCH(T) /* Bisecting search on tree */ 13 endif 14 return l 15 end Vertex r is found by an analogous RIGHTSEARCH function.

Convex hulls Dynamic hull (insertion) Finding l and r, 2 A distinct action is required to locate l and r in each of the 8 cases. Consider cases 1, 3, 5, and 7. Vertices l and r may not exist, because pi could be internal in cases 1 and 7. In these cases, if they exist l and r are in the same subtree of the root of T (the circled subtree in Figure 3. 16). Case Subtree (1) R(M) (3) L(M) (5) R(M) (7) L(M) The search calls itself recursively on that subtree until one of cases 2, 4, 6, 8 occurs, i. e. , l and r are in different subtrees of the current vertex. At that point the search proceeds as for those cases, i. e. , two separate searches (LEFTSEARCH and RIGHTSEARCH) are used to find l and r respectively. If a leaf of T is reached with finding any of cases 2, 4, 6, or 8, then pi is internal to Ci-1.

Convex hulls Dynamic hull (insertion) Finding l and r, 3 In general, finding l and r for pi involves tracing a single path in T from the root to the node where l and r must be in separate subtrees, and then following two paths to find l and r from there. T contains O(N) nodes (actually it has < i when pi is added, i N). Since T is balanced and therefore has O(log N) levels, and O(1) time is expended at each node on the two paths, the entire search requires O(log N) time.

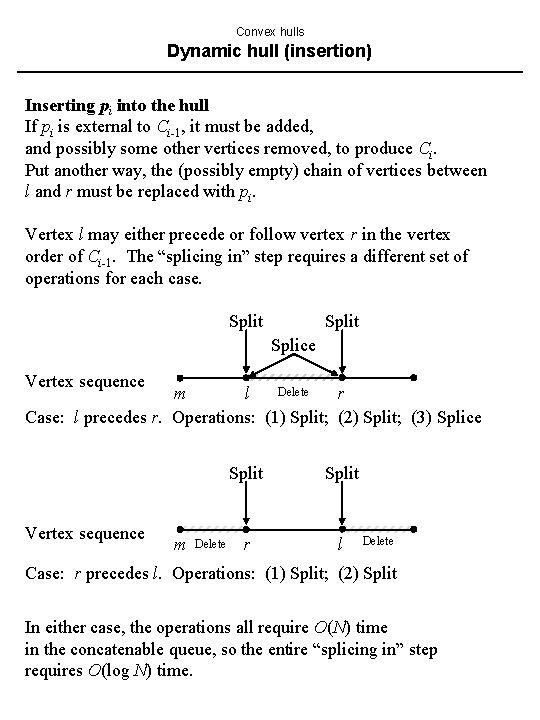
Convex hulls Dynamic hull (insertion) Inserting pi into the hull If pi is external to Ci-1, it must be added, and possibly some other vertices removed, to produce Ci. Put another way, the (possibly empty) chain of vertices between l and r must be replaced with pi. Vertex l may either precede or follow vertex r in the vertex order of Ci-1. The “splicing in” step requires a different set of operations for each case. Split Splice Vertex sequence Delete m l r Case: l precedes r. Operations: (1) Split; (2) Split; (3) Splice Vertex sequence m Delete Split r l Delete Case: r precedes l. Operations: (1) Split; (2) Split In either case, the operations all require O(N) time in the concatenable queue, so the entire “splicing in” step requires O(log N) time.

Convex hulls Dynamic hull (insertion) Analysis Each insertion requires O(log N) time: 1. O(log N) to find l and r 2. O(log N) to splice in pi For N insertions, the overall time is O(N log N). The storage required is O(N) for T.