CHAPTER 3 Transmission Line Line Parameters 1 3







































































- Slides: 85

CHAPTER 3 Transmission Line (Line Parameters) 1

3. 0 Transmission Line Introduction An electrical power transmission line can be modeled as series resistance, series inductance, shunt capacitance, and shunt conductance. A wire or combination of wires that are not insulated from one another is called conductor. Stranded conductor is composed of a group of wires, usually twisted or braided together. An overhead transmission line consists of conductors, insulators, support structures and shield wires. 2

3. 1 Conductors Types of Conductors In early days of the transmission line of electric power conductor were usually copper, but aluminum conductors have completely replaced copper for overhead lines because of its advantages • Reason of Using Aluminum Conductor 1. 2. 3. 3 The relative low cost compare to copper conductor. High strength-to-weight ratio as compared to copper. Aluminum is abundant supply while copper is limited in quantity.

3. 0 Conductor Types of Overhead Conductors Symbols identifying different types of aluminum overhead conductors are as follows: AAC All-aluminum conductors AAAC All-aluminum-alloy conductors ACSR Aluminum conductor, steel-reinforced ACAR Aluminum conductor, alloy-reinforced Expanded ACSR Filler (paper) separating inner steel strand from the outer aluminum strands. Normally used for EHV lines. 4

3. 0 Conductor Types of Overhead Conductors Aluminum-alloy conductors have higher tensile strength than the ordinary electric-conductor grade of aluminum. ACSR (Aluminum conductor, steel-reinforced) consist of a central core of steel strands surrounded by layers of aluminum strands. ACAR (Aluminum conductor, alloy-reinforced) consist of a central core of higher-strength aluminum surrounded by layers of aluminum strands. Cross section of steel-reinforced conductor, 7 steel strands, and aluminum strands or simply 24/7 5

3. 1 Line Resistance DC Resistance The resistance of the conductor is very important in transmission line evaluation and economic studies. The dc resistance of a solid round conductor at specific temperature is given by Where T = conductor resistivity at temperature T l = conductor length A = conductor cross-sectional area 6

3. 1 Line Resistance DC Resistance Conductor resistance depends on the following factors: 1) Spiraling 2) Temperature 3) Frequency (skin effect) 4) Current magnitude 7

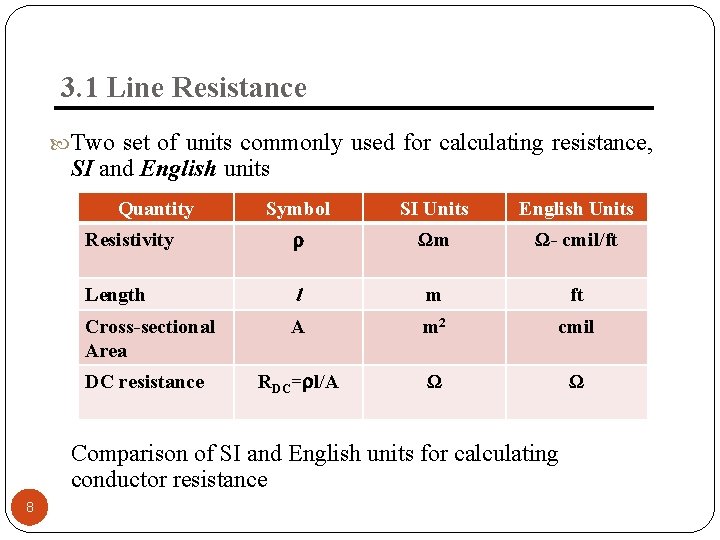
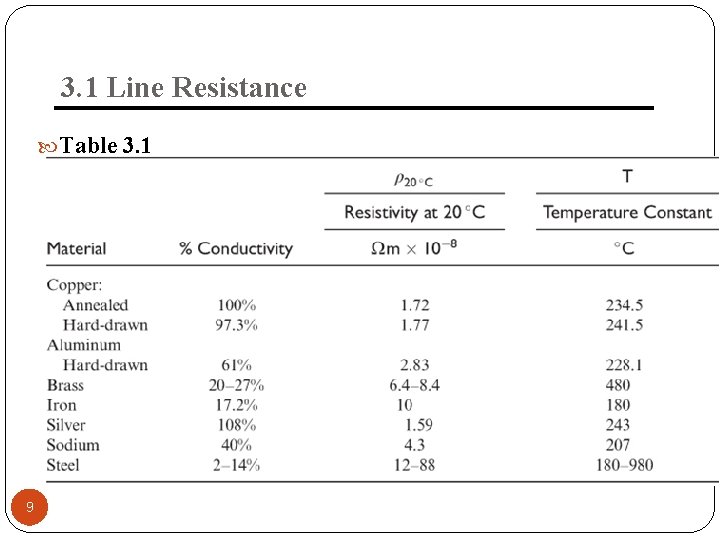
3. 1 Line Resistance Two set of units commonly used for calculating resistance, SI and English units Quantity Symbol SI Units English Units Resistivity Ωm Ω- cmil/ft Length l m ft Cross-sectional Area A m 2 cmil DC resistance RDC= l/A Ω Ω Comparison of SI and English units for calculating conductor resistance 8

3. 1 Line Resistance Table 3. 1 9

3. 1 Line Resistance In English units, conductor cross-sectional area is expressed in circular mils (cmil). A circular mil (cmil) is a unit of area, equal to the area of a circle with a diameter of one mil. The area in circular mils, A, of a circle with a diameter of d mils, is given by: • 1 circular mil (1 cmil) is equal to π/4 square mils, or π/4, 000 square inches • 1 mil = 1 x 10 -3 inch = 2. 54 x 10 -3 cm 10

3. 1 Line Resistance Example: Prove that 1 kcmil = 0. 05067 mm 2 Note: • 1 circular mil (1 cmil) is equal to π/4 square mils, or π/4, 000 square inches • 1 mil = 10 -3 inch = 2. 54 x 10 -3 cm 11

3. 1 Line Resistance Temperature Effects Increased resistance at conductor temperature rises Where: ρT 2 = conductor resistance at T 2 ρT 1 = conductor resistance at T 1, T 2 = temperature in C T = temperature constant = 234. 5 for annealed copper = 241. 0 for hard drawn copper = 28. 0 for hard drawn aluminum 12

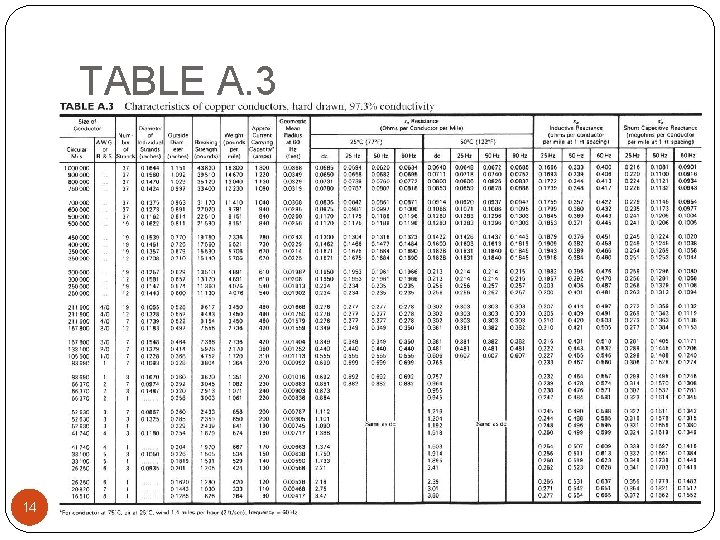
3. 1 Line Resistance Example Table A. 3 lists a 4/0 copper conductor with 12 strands. Strand diameter is 0. 3373 cm. For this conductor: a) Verify the total copper cross sectional area of 107. 2 mm 2 (211, 600 cmil in the table) b) Verify the dc resistance at 50 C of 0. 1876 Ω/km or 0. 302 Ω/mi. Assume a 2% increase in resistance due to spiraling. c) From Table A. 3, determine the percent increase in resistance at 60 Hz versus dc. 13

TABLE A. 3 14

3. 1 Line Resistance Solution a) The strand diameter is d = 0. 3373 cm x 10 mm/cm = 3. 373 mm and the strand area is b) Using hard drawn copper data from Table 3. 1 15

3. 1 Line Resistance The dc resistance at 50 C for a conductor length 1 km is c) 16 From Table A. 3,

3. 1 Line Resistance AC Resistance For dc, the current distribution is uniform throughout the conductor cross section. However, for ac, the current distribution is nonuniform. As frequency increases, the current in a solid cylindrical conductor tends to crowd toward the conductor surface, with smaller current density at the conductor center. This phenomenon is called skin effect. The ac resistance or effective resistance of a conductor is 17

3. 2 Inductance of a Single Conductor Introduction The inductance of a magnetic circuit that has a constant permeability can be obtained by determining the following: Magnetic field intensity H, from Ampere’s Law 2. Magnetic flux density B ( B= H) 3. Flux linkages 4. Inductance from flux linkages per ampere ( L= /I ) 1. (3. 2. 1) 18

3. 2 Inductance of a Single Conductor A current-carrying conductor produces a magnetic field around the conductor. Definition For non-magnetic material, the inductance L is the ratio of its total magnetic flux linkage ( ), to the current (I) Where: l= flux linkages (Wb-turns) I = current (A) (3. 2. 2) 19

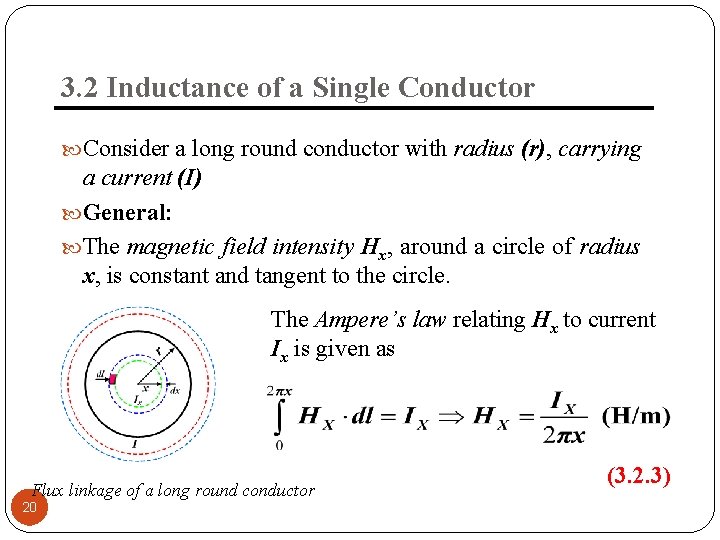
3. 2 Inductance of a Single Conductor Consider a long round conductor with radius (r), carrying a current (I) General: The magnetic field intensity Hx, around a circle of radius x, is constant and tangent to the circle. The Ampere’s law relating Hx to current Ix is given as Flux linkage of a long round conductor 20 (3. 2. 3)

3. 2 Internal Inductance Points inside of the conductor (x < r) Assuming uniform current density conductor cross section throughout the (3. 2. 4) Substituting Ix in (3. 2. 3) (3. 2. 5) For a nonmagnetic conductor with constant permeability μ 0= 4πx 10 -7 H/m, the magnetic flux density is given by Bx=μ 0 Hx, or (3. 2. 6) 21

3. 2 Internal Inductance Points inside of the conductor (x < r) (cont. ) The differential flux d for a small region of thickness dx and one meter length of conductor is (3. 2. 7) The flux dΦ links only the fraction of the conductor from the centre to radius x. The flux linkages dλ per meter of length, (3. 2. 8) 22

3. 2 Internal Inductance Points inside of the conductor (x < r) (cont. ) The total flux linkage is found by integrating d X from 0 to r (3. 2. 9) The inductance due to internal flux linkage (3. 2. 10) 23

3. 3 Inductance Due to External Flux Linkage Points outside of the conductor (x > r) Consider Hx external to the conductor at radius x > r as shown in figure below, since the circle at radius x encloses the entire current, Ix = I and in (3. 2. 3) Ix is replaced by I and the flux density at radius x becomes (3. 2. 11) 24

3. 3 Inductance Due to External Flux Linkage Points outside of the conductor (x > r) (cont. ) Since the entire current I is linked by the flux outside the conductor, the flux linkage dλx is numerically equal to the flux dΦx. The differential flux dΦx for small region of thickness dx and one meter length of the conductor is given by (3. 2. 12) The external flux linkage between two points D 1 and D 2 is found by integrating dλx from D 1 to D 2. (3. 2. 13) 25

3. 3 Inductance Due to External Flux Linkage Points outside of the conductor (x > r) (cont. ) The inductance between two points external to a conductor (3. 2. 14) 26

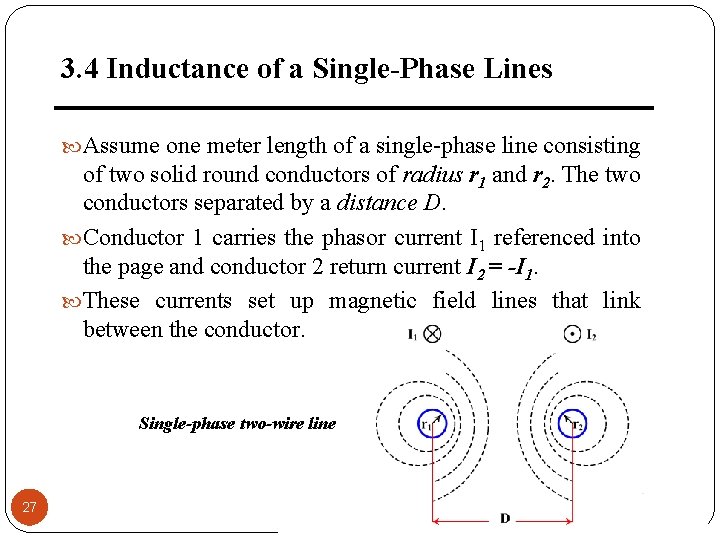
3. 4 Inductance of a Single-Phase Lines Assume one meter length of a single-phase line consisting of two solid round conductors of radius r 1 and r 2. The two conductors separated by a distance D. Conductor 1 carries the phasor current I 1 referenced into the page and conductor 2 return current I 2 = -I 1. These currents set up magnetic field lines that link between the conductor. Single-phase two-wire line 27

3. 4 Inductance of a Single-Phase Lines Total inductance of conductor 1, L 1=L 1(int)+L 1(ext) (3. 4. 1) 28

3. 4 Inductance of a Single-Phase Lines Let The total inductance of conductor 1 becomes (3. 4. 2) Similarly the total inductance of conductor 2 (3. 4. 3) If the two conductor are identical r 1=r 2=r and L 1=L 2=L, the inductance per conductor per meter length (3. 4. 4) 29

3. 4 Inductance of a Single-Phase Lines The term r’ is known mathematically as self-geometric mean distance of a circle with radius r is abbreviated as GMR is commonly referred to as geometric mean radius and designated as Ds (3. 4. 5) The inductance per conductor in milihenries per kilometers becomes (3. 4. 6) 30

3. 5 Inductance of Composite Conductors Single-phase Line With 2 Composite Conductor x and y Single phase line with two composite conductor • Conductor x consist of n identical strand or subconductor, each with radius rx • Conductor y consist of m identical strand or subconductor, each with radius ry Assumed current to be equally divided among the subconductors. The current per strand is I/n in x and I/m in y 31

3. 5 Inductance of Composite Conductors Flux Linkage of Conductor a (3. 5. 1) Inductance of Subconductor a (3. 5. 2) Inductance of Subconductor n (3. 5. 3) 32

3. 5 Inductance of Composite Conductors Average Inductance Of any one Subconductor in Group x Due to all the subconductors of x in parallel, Inductance x Final Lx by substituting La, Lb, Lc , …. , Ln into above equation (3. 5. 4) 33

3. 5 Inductance of Composite Conductors Geometric Mean Distance (GMD) The mnth root of the product of the mnth distances between n strands of conductor x and m strand conductor y. Geometric Mean Radius (GMRx) (3. 5. 5) The n 2 root of the product of the n 2 terms consisting of r’ of every strand times the distance from each strand to all other strands within group x. (3. 5. 6) 34

3. 5 Inductance of Composite Conductors Example 3. 1 (GMR, GMD and inductance: single phase two conductor line) Determine the GMD and GMR for conductor X and Y and evaluate the total inductance for the both conductor line as shown in following figure. 35

3. 5 Inductance of Composite Conductors Solution The GMD between conductor x and conductor y The GMR for conductor x The GMR for conductor 36

3. 5 Inductance of Composite Conductors Evaluating Dxy, Dxx and Dyy 37

3. 5 Inductance of Composite Conductors The indctance of conductor x 38

3. 5 Inductance of Composite Conductors The inductance of conductor y The total inductance of the two conductor line 39

3. 5 Inductance of Composite Conductors Example 3. 2 (Inductance and inductive reactance: single phase line) A single phase line operating at 60 Hz consist of two 4/0 12 -strand copper conductor with 1. 5 m spacing between conductor centers. The line length is 32 km. Determine the total inductance in H and the total inductive reactance in Ω. 40

3. 5 Inductance of Composite Conductors 41

3. 5 Inductance of Composite Conductors Solution: The GMD between conductor centers is Dxy = 1. 5 m. Also, from Table A. 3, the GMR of a 4/0 12 -strand copper conductor is Dxx = Dyy= 0. 0175 ft or 0. 5334 cm. The inductance of conductor x and y are 42

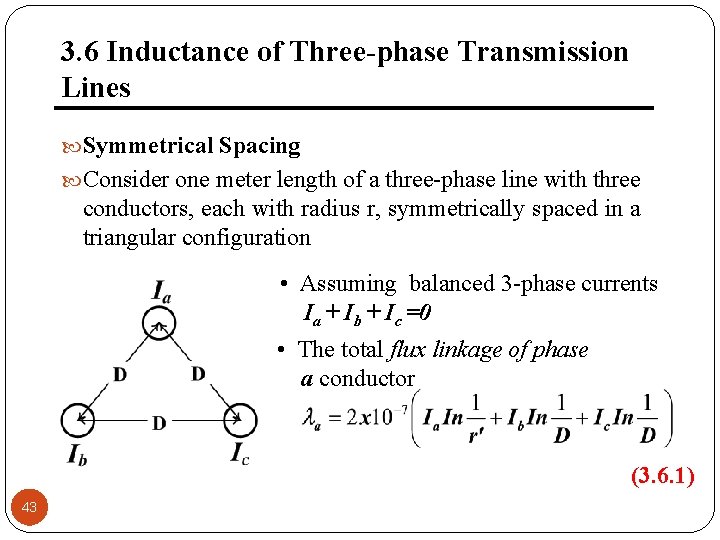
3. 6 Inductance of Three-phase Transmission Lines Symmetrical Spacing Consider one meter length of a three-phase line with three conductors, each with radius r, symmetrically spaced in a triangular configuration • Assuming balanced 3 -phase currents Ia + Ib + Ic =0 • The total flux linkage of phase a conductor (3. 6. 1) 43

3. 6 Inductance of Three-phase Transmission Lines Symmetrical Spacing (cont. ) Substituting for Ib+ Ic = -Ia (3. 6. 2) Due to symmetry, a= b= c , and the three inductances are identical. The inductance per phase per km length 44 (3. 6. 3)

3. 6 Inductance of Three-phase Transmission Lines Asymmetrical Spacing In practical transmission line is asymmetrical spacing of conductor because of construction consideration. In asymmetrical spacing, voltage drop due to line inductance will be unbalanced • In 3 -phase line with asymmetrical spacing, the flux linkages (3. 6. 4) 45

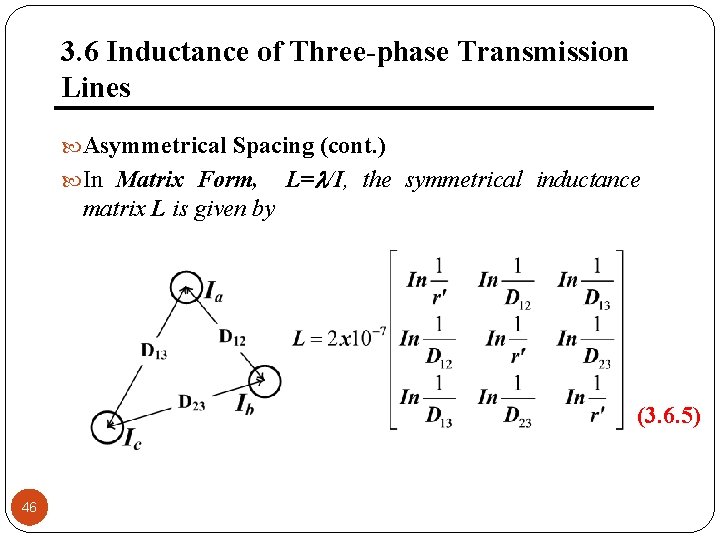
3. 6 Inductance of Three-phase Transmission Lines Asymmetrical Spacing (cont. ) In Matrix Form, L= /I, the symmetrical inductance matrix L is given by (3. 6. 5) 46

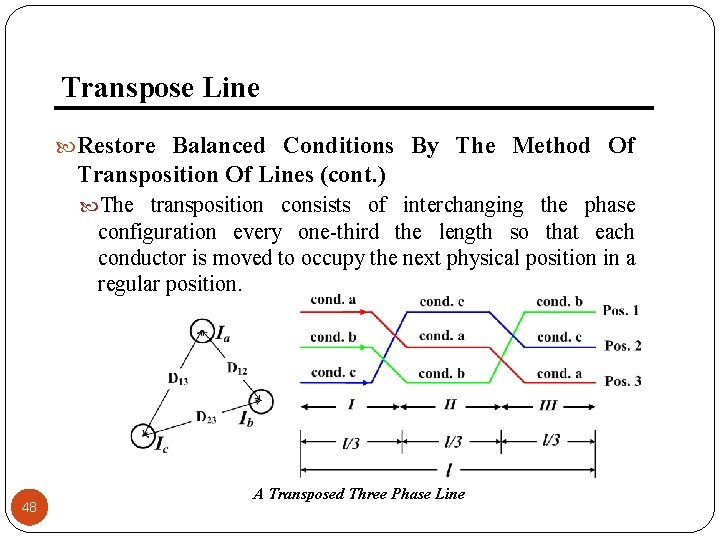
3. 6. 1 Transpose Line Asymmetrical spacing causes the flux linkages and therefore the inductance of each phase to be different resulting in unbalanced receiving-end voltages even when sending-end voltages and line currents are balanced. Also voltages will be induced in adjacent communication lines even when line currents are balanced. Restore Balanced Conditions By The Method Of Transposition Of Lines Average inductance of each phase will be the same Each phase occupies each position for the same fraction of the total length of the line 47

Transpose Line Restore Balanced Conditions By The Method Of Transposition Of Lines (cont. ) The transposition consists of interchanging the phase configuration every one-third the length so that each conductor is moved to occupy the next physical position in a regular position. 48 A Transposed Three Phase Line

Transpose Line Flux linkages of conductor a, when a is in position 1, b in position 2 and c in position 3, the flux linkages for a are (3. 6. 6) when a is in position 2, b in position 3 and c in position 1, the flux linkages for a are (3. 6. 7) when a is in position 3, b in position 1 and c in position 2, the flux linkages for a are 49 (3. 6. 8)

Transpose Line The average value of the flux linkages of a is (3. 6. 9) With the restriction that Ia =-(Ib + Ic) , the average flux linkages of a is (3. 6. 10) 50

Transpose Line OR , The average inductance per phase is (3. 6. 11) (3. 6. 12) Where, Geometric Mean Distance (GMD) Ds Geometric Mean Radius (GMR) 51 (3. 6. 13) (3. 6. 14)

Transpose Line Example 3. 4 (Inductance and inductive reactance: three phase line) 52

53

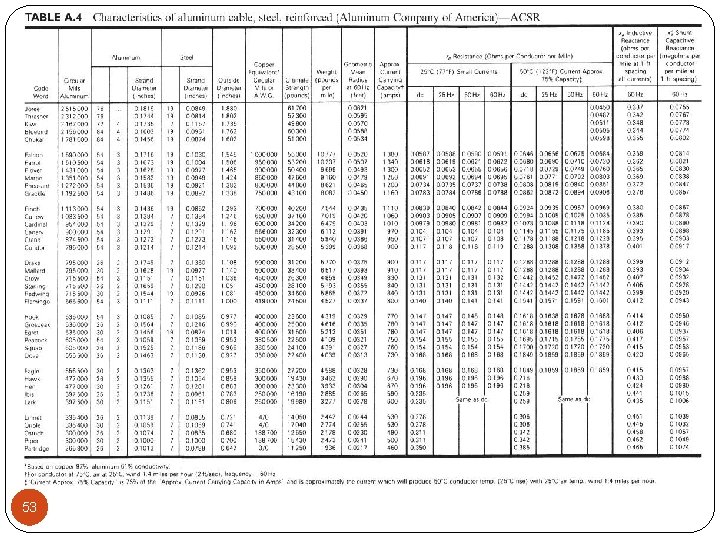
Transpose Line Solution From Table A. 4, the GMR of a 806 mm 2 (1, 590, 00 cmil) 54/3 ACSR conductor is Also, from 3. 6. 7 and 3. 6. 8, The inductive reactance of phase a 54

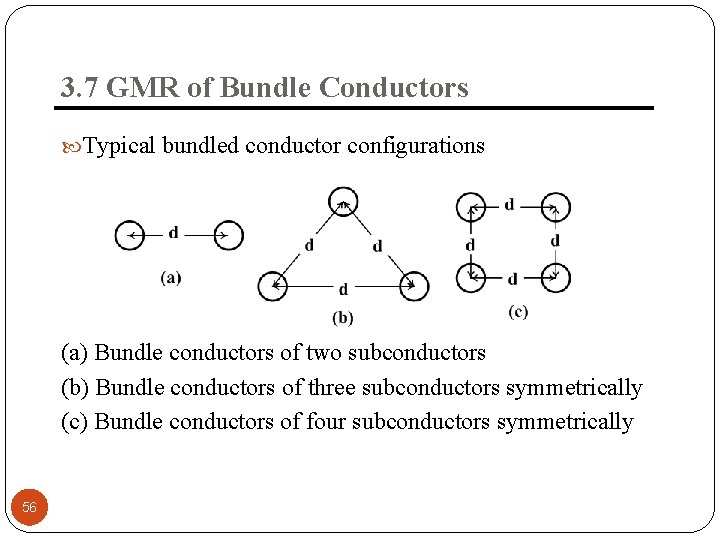
3. 7 GMR of Bundle Conductors Introduction Used on overhead lines above 230 k. V (EHV) Some of the advantages Reduces the line reactance, improves the line performance and increase power capability of the line. Reduces the voltage surface gradient, reduce corona loss, radio interference and surge impedance Typical bundled conductors consists of two, three or four subconductors symmetrically arranged 55

3. 7 GMR of Bundle Conductors Typical bundled conductor configurations (a) Bundle conductors of two subconductors (b) Bundle conductors of three subconductors symmetrically (c) Bundle conductors of four subconductors symmetrically 56

3. 7 GMR of Bundle Conductors The GMR of the equivalent single conductor is obtained by using (3. 5. 6). Each conductor is first replaced by an equivalent solid cylindrical conductor with GMR = DS. Then, the bundle is replaced by one equivalent conductor with GMR = DSL For The Two-subconductor Bundle (3. 7. 1) For The Three-subconductor Bundle 57 (3. 7. 2)

3. 7 GMR of Bundle Conductors For The Four-subconductor Bundle (3. 7. 3) The inductance is then (3. 7. 4) 58

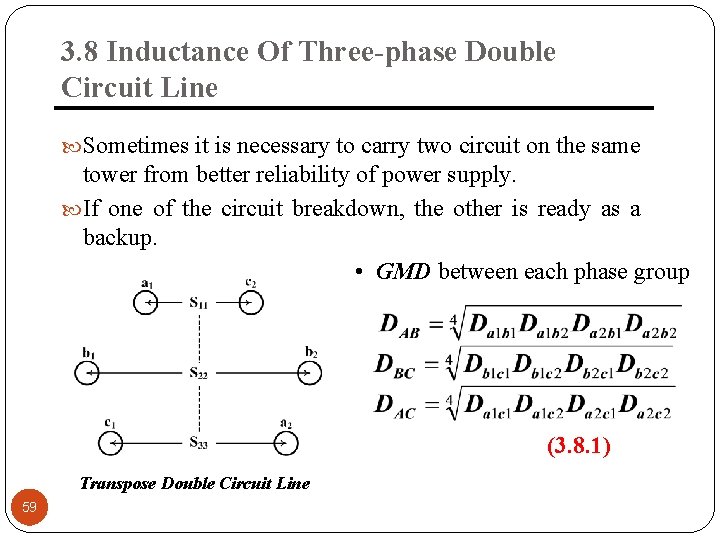
3. 8 Inductance Of Three-phase Double Circuit Line Sometimes it is necessary to carry two circuit on the same tower from better reliability of power supply. If one of the circuit breakdown, the other is ready as a backup. • GMD between each phase group (3. 8. 1) Transpose Double Circuit Line 59

3. 8 Inductance Of Three-phase Double Circuit Line Equivalent GMD per phase (3. 8. 2) GMR of each phase group (3. 8. 3) Equivalent GMR For Per Phase Inductance To Neutral Inductance Per Phase (3. 8. 4) 3. 8. 5) 60

3. 8 Inductance Of Three-phase Double Circuit Line Example 3. 5 Each conductor in example 3. 4 is replaced by two (795 000 cmil) 403 mm 2 ACSR 26/2 conductors, as shown in Figure 3. 5. Bundle spacing is 0. 4 m. Flat horizontal spacing is retained, with 10 m between adjacent bundle centers. Calculate the inductive reactance of the line and compare it with that of Example 3. 4. 61 Figure 3. 5: Three phase bundled conductor line

3. 8 Inductance Of Three-phase Double Circuit Line Solution From Table A. 4, the GMR of a 403 mm 2 (795, 000 cmil) 26/2 ACSR 26/2 conductor (3. 7. 1) 62

3. 8 Inductance Of Three-phase Double Circuit Line Solution The inductive reactance The reactance of the bundled line, 78. 8 Ω, is 22% less than that in Example 3. 4, even though the two conductor bundle has the same amount of conductor material (that is the same cmil per phase). One advantage of reduced series line reactance is smaller line voltage drop. Also, the loadability of medium and long EHV line is increased. 63

3. 9 Line Capacitance Introduction The capacitance between conductors in a medium with constant permittivity can be obtain by determining the following: 64 1. 2. 3. Electric field strength E, From Gauss’s Law Voltage between conductors Capacitance from charge per unit volt (C = q / v) • Gauss’s law states that the total electric flux leaving a closed surfaced equals the total charge within the volume enclosed by the surface.

3. 9 Line Capacitance Definition The capacitance C is the ratio of charge q to the voltage V (3. 9. . 1) where, C= Capacitance Between a Pair of Cond. in Farads q= Charge in Conductor in Coulombs V= Voltage Between Cond. in Volts 65

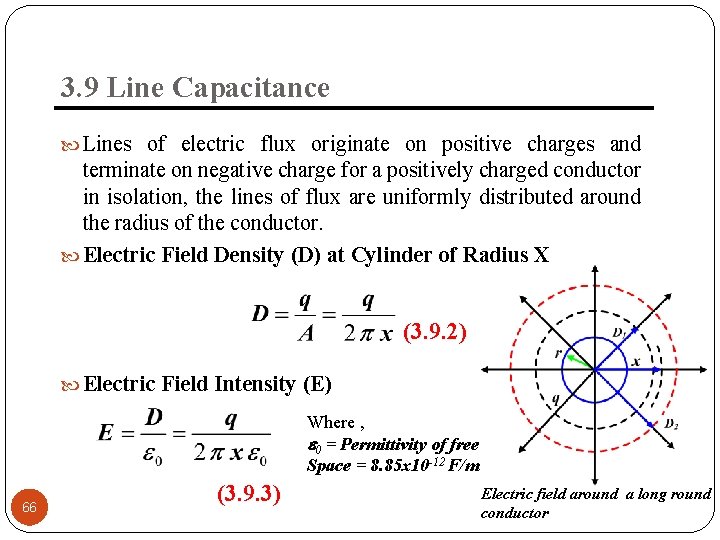
3. 9 Line Capacitance Lines of electric flux originate on positive charges and terminate on negative charge for a positively charged conductor in isolation, the lines of flux are uniformly distributed around the radius of the conductor. Electric Field Density (D) at Cylinder of Radius X (3. 9. 2) Electric Field Intensity (E) Where , 0 = Permittivity of free Space = 8. 85 x 10 -12 F/m 66 (3. 9. 3) Electric field around a long round conductor

3. 9 Line Capacitance Potential difference from position D 1 to D 2 is defined as the work done in moving a unit charge of one coulomb from D 2 to D 1 through the electric field produced by the charge on the conductor. Potential Difference Between Two Points P 1 And P 2 (3. 9. 4) 67

3. 10 Capacitance of Single-phase and Three Phase Line with Equal Phase Spacing Consider the single phase two wire line in Figure 3. 10. Assume conductor x have a charge of q C/m, and conductor y has an equal quantity negative charge –q. then the voltage between conductor (3. 10. 1) 68 Figure 3. 10

3. 10 Capacitance of Single-phase and Three Phase Line with Equal Phase Spacing Using Dxy= Dyx= D, Dxx = rx and Dyy = ry the voltage between conductor (3. 10. 2) Capacitance between Conductor (line to line) If rx = ry = r (3. 10. 3) 69

3. 10 Capacitance of Single-phase and Three Phase Line with Equal Phase Spacing • Line to neutral capacitance (3. 10. 4) Circuit representation of capacitances for a single phase two wire line 70

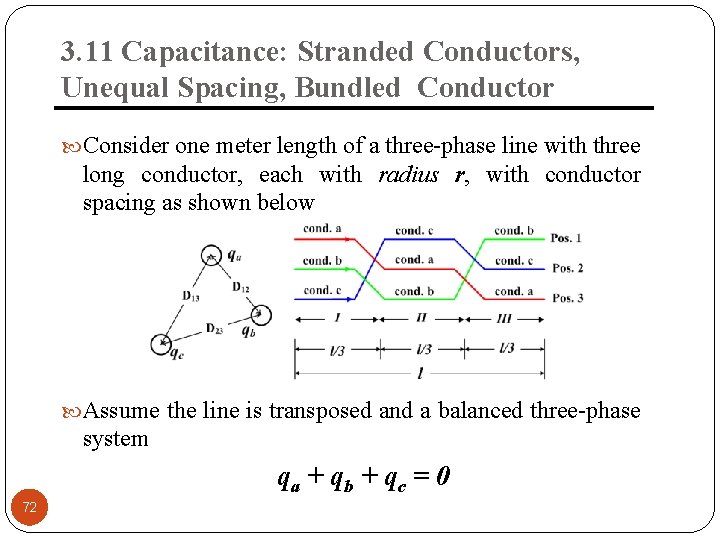
3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Consider n parallel long conductors with charges q 1, q 2, . . qn coulombs/meter. Assume no distortion effect and charge uniformly distributed around the conductor with the following constraint q 1+q 2+……+qn = 0 The potential different between conductor I and j due to presence of all charges is (3. 11. 1) When k = i , Dii is the distance between surface of the conductor and its center, namely its radius r. 71 Multiconductor configuration

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Consider one meter length of a three-phase line with three long conductor, each with radius r, with conductor spacing as shown below Assume the line is transposed and a balanced three-phase system qa + qb + qc = 0 72

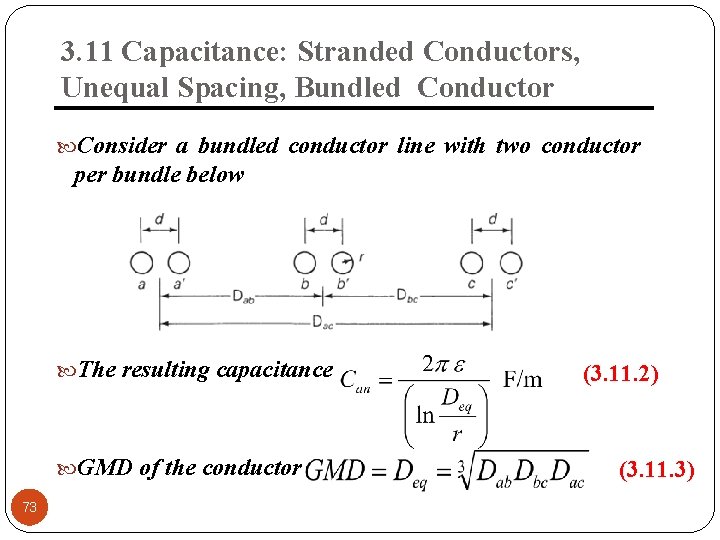
3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Consider a bundled conductor line with two conductor per bundle below The resulting capacitance GMD of the conductor 73 (3. 11. 2) (3. 11. 3)

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor (3. 11. 4) 74

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Capacitance Per Phase In Bundle Conductors (3. 11. 5) Equivalent radius DSC for two-subconductor bundle for three-subconductor bundle (3. 11. 6) (3. 11. 7) for four-subconductor bundle (3. 11. 8) 75

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor The current supplied to the transmission line capacitance is called charging current. For a single phase circuit operating at line to line voltage Vxy = Vxy 0°, the charging current is (3. 11. 9) The reactive power delivered by the line to line capacitance is 76 (3. 11. 10)

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor For a completely transposed three phase line that has balance positive sequence voltages with Van = VLN 0°, the phase a charging current is (3. 11) The active power delivered by phase a is (3. 11. 12) The total reactive power supplied by three phase line (3. 11. 13) 77

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Example 3. 6 Solution From Table A. 3, the outside radius of a 4/0 12 strands copper conductor is 78

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Line to line capacitance (3. 10. 3) Or the reactive power (3. 11. 10) 79

3. 5 Inductance of Composite Conductors Example 3. 2 (Inductance and inductive reactance: single phase line) A single phase line operating at 60 Hz consist of two 4/0 12 -strand copper conductor with 1. 5 m spacing between conductor centers. The line length is 32 km. Determine the total inductance in H and the total inductive reactance in Ω. 80

3. 5 Inductance of Composite Conductors 81

3. 5 Inductance of Composite Conductors Solution: The GMD between conductor centers is Dxy = 1. 5 m. Also, from Table A. 3, the GMR of a 4/0 12 -strand copper conductor is Dxx = Dyy= 0. 0175 ft or 0. 5334 cm. The inductance of conductor x and y are 82

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Example 3. 7 For the three phase line in Example 3. 5, determine the capacitance to neutral in F and the shunt admittance to neutral in S. if the line voltage is 345 k. V, determine the charging current in k. A per phase and the total reactive power in Mvar supplied by line capacitance. Assume balanced positive sequence voltages. 83

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Solution From Table A. 4, the outside radius of a 403 mm 2 26/2 ACSR conductor is (3. 11. 6) 3. 5 84 (3. 11. 5)

3. 11 Capacitance: Stranded Conductors, Unequal Spacing, Bundled Conductor Solution (3. 11) (3. 11. 13) 85
 Z parameters of t network
Z parameters of t network Transmission line example problems
Transmission line example problems Transmission line examples
Transmission line examples Rangkaian ekivalen saluran transmisi
Rangkaian ekivalen saluran transmisi Microstrip transmission line
Microstrip transmission line Microstrip transmission line
Microstrip transmission line Mechanical design of transmission line
Mechanical design of transmission line Two wire transmission line
Two wire transmission line Attenuation constant formula
Attenuation constant formula Metallic transmission lines
Metallic transmission lines Matched line transmission
Matched line transmission L
L Abcd short
Abcd short Lossless transmission line
Lossless transmission line Chapter 19 disease transmission and infection prevention
Chapter 19 disease transmission and infection prevention Chapter 19 disease transmission and infection prevention
Chapter 19 disease transmission and infection prevention Chapter 15:8 using sterile techniques
Chapter 15:8 using sterile techniques Chapter 19 disease transmission and infection prevention
Chapter 19 disease transmission and infection prevention Classification of surveying
Classification of surveying Xcopy parameters
Xcopy parameters Lesson 4: parameters and return make
Lesson 4: parameters and return make Lesson 3: parameters and return practice
Lesson 3: parameters and return practice Lennard-jones parameters table
Lennard-jones parameters table Z parameters of t network
Z parameters of t network 5 parameters in asl
5 parameters in asl Zener diode parameters
Zener diode parameters Lossless network s-parameters
Lossless network s-parameters Scaling factors for device parameters in vlsi
Scaling factors for device parameters in vlsi Uplink design in satellite communication
Uplink design in satellite communication Actual parameters in c
Actual parameters in c Vertial
Vertial Population of interest
Population of interest Gaussian function parameters
Gaussian function parameters Building blocks of thermal system
Building blocks of thermal system Concatenation of macro parameters
Concatenation of macro parameters Ruby keyword arguments
Ruby keyword arguments Mean effective pressure formula
Mean effective pressure formula Robo analyzer
Robo analyzer Arguments vs parameters
Arguments vs parameters Evaluation of semisolid dosage form
Evaluation of semisolid dosage form S-parameters basics
S-parameters basics Variation of parameters
Variation of parameters Variation parameter
Variation parameter Actual parameters in c
Actual parameters in c Pooling stride
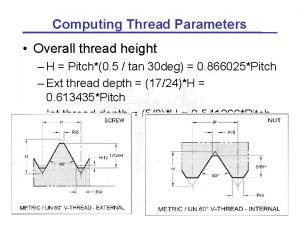
Pooling stride Thread parameters
Thread parameters Common critical values
Common critical values Metabolic acidosis correction formula
Metabolic acidosis correction formula Gaussian function parameters
Gaussian function parameters Abg parameters
Abg parameters Z parameters
Z parameters Normal abg levels
Normal abg levels The variable for fbd control parameters includes:
The variable for fbd control parameters includes: Docker parameters
Docker parameters Lesson 3 parameters and return practice 8
Lesson 3 parameters and return practice 8 Sap crm transaction launcher
Sap crm transaction launcher Technical performance measures
Technical performance measures Cayley klein parameters
Cayley klein parameters For counting the number of positional parameters
For counting the number of positional parameters Multinomial distribution formula
Multinomial distribution formula Mintzbergs 5 ps
Mintzbergs 5 ps Intrinsic parameters of food
Intrinsic parameters of food Esp course design sample
Esp course design sample Verilog nested generate
Verilog nested generate Master planning parameters ax 2012
Master planning parameters ax 2012 Midpoint ellipse drawing algorithm
Midpoint ellipse drawing algorithm Recursive macro expansion
Recursive macro expansion Fundamental parameters of antenna
Fundamental parameters of antenna Basics of instrumentation and control ppt
Basics of instrumentation and control ppt Palm orientation in asl example
Palm orientation in asl example Faktor yang mempengaruhi ukuran lapangan terbang
Faktor yang mempengaruhi ukuran lapangan terbang Dram timing
Dram timing The associative mapping is costlier than direct mapping.
The associative mapping is costlier than direct mapping. Group discussion parameters
Group discussion parameters Cosc parameters
Cosc parameters Cad parameters
Cad parameters C programming return statement
C programming return statement Strain life parameters ansys
Strain life parameters ansys Undetermined coefficients
Undetermined coefficients Poisson random variable pdf
Poisson random variable pdf Parameters of binomial distribution
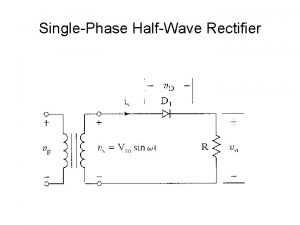
Parameters of binomial distribution Single phase half wave rectifier
Single phase half wave rectifier Python toolbox parameters
Python toolbox parameters What is projection welding
What is projection welding Aacap practice parameters
Aacap practice parameters Semen parameters
Semen parameters