Computer Graphics CC 416 Lecture 05 Midpoint Ellipse

Computer Graphics CC 416 Lecture 05: Mid-point Ellipse algorithm Dr. Manal Helal – Fall 2014

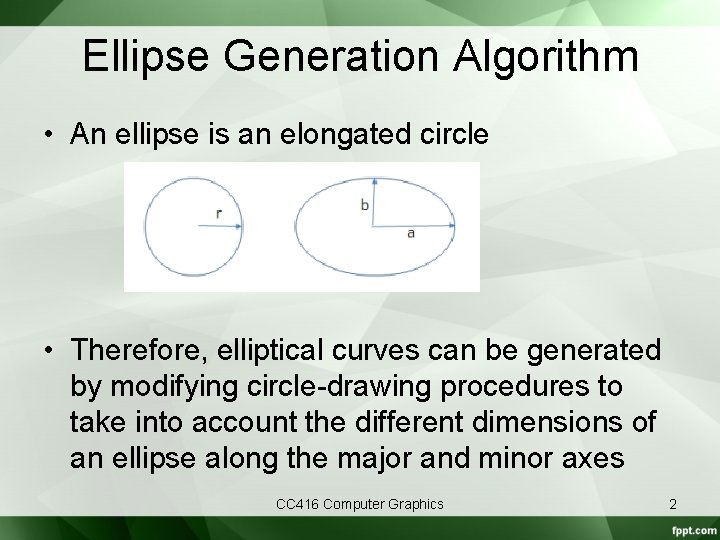
Ellipse Generation Algorithm • An ellipse is an elongated circle • Therefore, elliptical curves can be generated by modifying circle-drawing procedures to take into account the different dimensions of an ellipse along the major and minor axes CC 416 Computer Graphics 2

• Start with the basic equation of a circle • Divide both sides by r 2 yc ry (x, y) rx xc • The general equation of an ellipse can be stated as CC 416 Computer Graphics 3

Properties of Ellipses • An ellipse is defined as the set of points such that the sum of the distances from two fixed positions (foci) is the same for all points d 2 CC 416 Computer Graphics d 1 4

• So d 2 d 1 • Expressing distances d 1, and d 2, in terms of the focal coordinates F 1 = (x 1, y 1) and F 2 = (x 2, y 2), we have CC 416 Computer Graphics 5

• Symmetry considerations can be used to further reduce computations. • An ellipse in standard position is symmetric between quadrants, but unlike a circle, it is not symmetric between the two octants of a quadrant. • Thus, we must calculate pixel positions along the elliptical arc throughout one quadrant, then we obtain positions in the remaining three quadrants by symmetry CC 416 Computer Graphics 6

Mid-Point Ellipse Algorithm • The approach is similar to that used in displaying a circle • Given parameters rx, ry, and (xc, yc), we determine points (x, y) for an ellipse in standard position centered on the origin • Then the points are shifted so the ellipse is centered at (xc, yc) CC 416 Computer Graphics 7

• The mid-point ellipse method is applied throughout the first quadrant in two parts • This is done according to the slope of the tangent – When slope < -1, take unit steps in the x direction – When slope > -1, take unit steps in the y direction CC 416 Computer Graphics 8

• From equation • When (xc, yc) = (0, 0) • the decision parameter will be according to CC 416 Computer Graphics 9

• So, the next pixel along the ellipse path according to the sign of the ellipse function evaluated at the midpoint between the two candidate pixels CC 416 Computer Graphics 10

• Starting at (0, ry) – take unit steps in the x direction until reaching the boundary between region 1 and region 2 – switch to unit steps in the y direction over the remainder of the curve in the first quadrant – At each step, test the value of the slope using CC 416 Computer Graphics 11

• At the boundary between region 1 and region 2, dy/dx = - 1 and • Therefore, we move out of region 1 whenever CC 416 Computer Graphics 12

• Recall • Assuming position (xk, yk) has been selected at the previous step • the next position along the ellipse path is determined by evaluating the decision parameter CC 416 Computer Graphics 13

• If p 1 k < 0, the midpoint is inside the ellipse and the pixel on scan line y, is closer to the ellipse boundary. • Otherwise, the mid position is outside or on the ellipse boundary, and we select the pixel on scan line yk - 1. CC 416 Computer Graphics 14

• At the next sampling position (xk+1+1 = xk + 2), the decision parameter for region 1 is evaluated as [(xk+1) + 1]2 = (xk+1)2 + 2(xk+1) + 1 [(Yk+1 -(1/2))]2 = Yk+12 - Yk+1 + (1/4) P 1 k+1 = ry 2(xk+1)2 + 2 ry 2 (xk+1) + ry 2 +(rx 2 Yk+12 - rx 2 Yk+1 + rx 2 (1/4)) - rx 2 ry 2 P 1 k • where yk+1 is either yk or yk - 1, depending on the sign of p 1 k CC 416 Computer Graphics 15

• So decision parameters are incremented by the following amounts: CC 416 Computer Graphics 16

• In region 1, the initial value of the decision parameter is obtained by evaluating the ellipse function at the start position (x, y) = (0, ry) or CC 416 Computer Graphics 17

• In region 2, we sample at unit steps in the negative y direction • The midpoint is now taken between horizontal pixels at each step • The decision parameter is evaluated as CC 416 Computer Graphics 18

• If p 2 k > 0, the mid-position is outside the ellipse boundary, and we select the pixel at xk • If p 2 k ≤ 0, the midpoint is inside or on the ellipse boundary, and we select pixel position xk+1 CC 416 Computer Graphics 19

When we enter region 2, the initial position (x 0, y 0) is taken as the last position selected in region 1 and the initial decision parameter in region 2 is then CC 416 Computer Graphics 20

• To simplify the calculation of p 20, we could select pixel positions in counterclockwise order starting at (rx, 0). • Unit steps would then be taken in the positive y direction up to the last position selected in region 1 CC 416 Computer Graphics 21

• The midpoint algorithm can be adapted to generate an ellipse in nonstandard position • Where transformation methods can be used to reorient the ellipse Non Standard position CC 416 Computer Graphics 22

• Midpoint Ellipse Algorithm 1. Input rx, ry and ellipse center (xc, yc), and obtain the first point on an ellipse centered on the origin as 2. Calculate the initial value of the decision parameter in region 1 as CC 416 Computer Graphics 23

2. At each x position in region 1, starting at k = 0, perform the following test: If p 1 k < 0, the next point along the ellipse centered on (0, 0) is (xk+1, yk) and Otherwise, the next point along the circle is (xk + 1, yk – 1) CC 416 Computer Graphics 24

With and continue until CC 416 Computer Graphics 25

4. Calculate the initial value of the decision parameter in region 2 using the last point (x 0, y 0) calculated in region 1 as CC 416 Computer Graphics 26

5. At each yk position in region 2, starting at k = 0, perform the following test: If p 2 k> 0, the next point along the ellipse centered on (0, 0) is (xk, yk - 1) and Otherwise, the next point along the circle is (xk + 1, yk - 1) and using the same incremental calculations for x and y as in region 1. CC 416 Computer Graphics 27

6. Determine symmetry points in the other three quadrants. 7. Move each calculated pixel position (x, y) onto the elliptical path centered on (xc, yc) and plot the coordinate values: x = x + xc y = y + yc CC 416 Computer Graphics 28

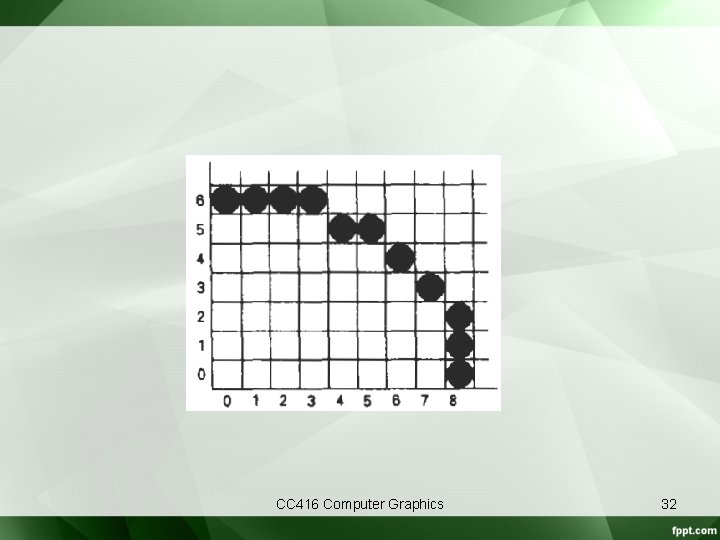
• Example – Given rx = 8 and ry = 6, rx 2 = 64 and ry 2 = 36 – Initial values and increments for the decision parameter calculations are – For region 1: • The initial point for the ellipse centered on the origin is (x 0, y 0) = (0, 6), and the initial decision parameter value is • Applying the following when p 1 k < 0 • Otherwise: • Loop until CC 416 Computer Graphics 29

• Successive decision parameter values and positions along the ellipse path are calculated using the midpoint method as • We now move out of region 1, since CC 416 Computer Graphics 30

– For region 2 rx = 8 and ry = 6, rx 2 = 64 and ry 2 = 36 • the initial point is (x 0, y 0) = (7, 3) and the initial decision parameter is • The remaining positions along the ellipse path in the first quadrant are then calculated as: • If If p 2 k> 0: • Else: k p 2 k Xk+1 Yk+1 2 r 2 y. Xk+1 0 -23 8 2 72*8 = 576 128*2 = 256 1 (-23+256+64)= 297 8 1 576 2 (297+576 -128+64) = 809 CC 416 Computer Graphics 8 0 - 2 r 2 x. Yk+1 128 - 31

CC 416 Computer Graphics 32

More about ellipses • Source: http: //en. wikipedia. org/wiki/Ellipse CC 416 Computer Graphics 33