Algorithmic Game Theory New Market Models and Internet































































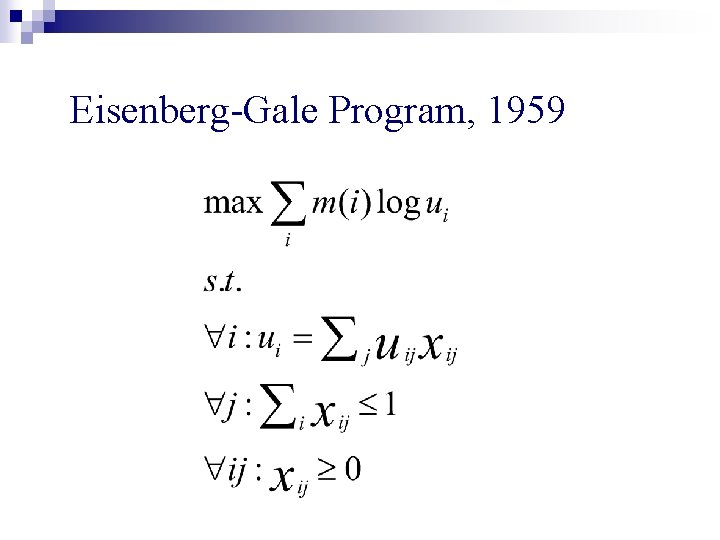















![Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-127.jpg)
![Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-128.jpg)
![3 -source branching Single-source 2 s-s undir SUA Comb EG[2] 2 s-s dir Fisher 3 -source branching Single-source 2 s-s undir SUA Comb EG[2] 2 s-s dir Fisher](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-129.jpg)









- Slides: 138

Algorithmic Game Theory New Market Models and Internet Computing and Algorithms Vijay V. Vazirani

Markets

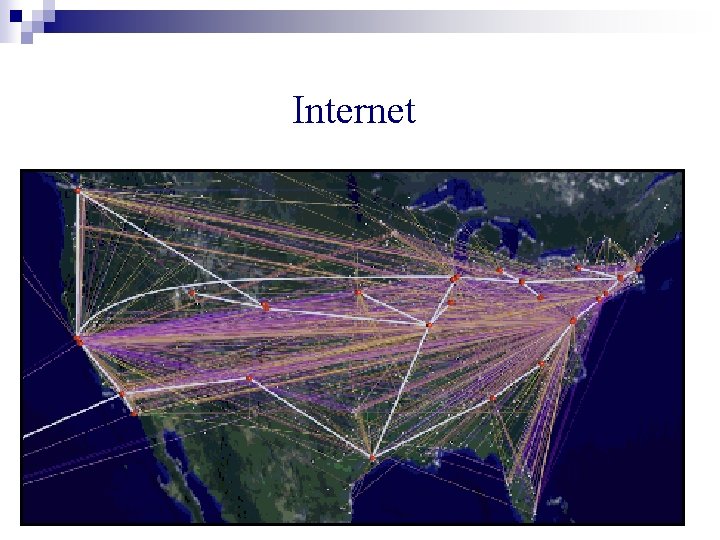
Stock Markets

Internet

n Revolution in definition of markets

n Revolution in definition of markets n New markets defined by ¨ Google ¨ Amazon ¨ Yahoo! ¨ Ebay

n Revolution in definition of markets n Massive computational power available for running these markets in a centralized or distributed manner

n Revolution in definition of markets n Massive computational power available for running these markets in a centralized or distributed manner n Important to find good models and algorithms for these markets

Theory of Algorithms n Powerful tools and techniques developed over last 4 decades.

Theory of Algorithms n Powerful tools and techniques developed over last 4 decades. n Recent study of markets has contributed handsomely to this theory as well!

Adwords Market n Created by search engine companies ¨ Google ¨ Yahoo! ¨ MSN n Multi-billion dollar market n Totally revolutionized advertising, especially by small companies.




New algorithmic and game-theoretic questions n Monika Henzinger, 2004: Find an on-line algorithm that maximizes Google’s revenue.

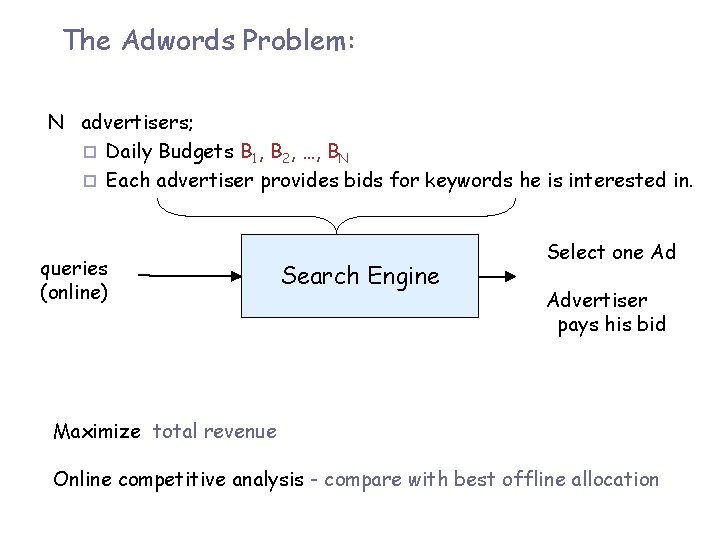
The Adwords Problem: N advertisers; ¨ Daily Budgets B 1, B 2, …, BN ¨ Each advertiser provides bids for keywords he is interested in. Search Engine

The Adwords Problem: N advertisers; ¨ Daily Budgets B 1, B 2, …, BN ¨ Each advertiser provides bids for keywords he is interested in. queries (online) Search Engine

The Adwords Problem: N advertisers; ¨ Daily Budgets B 1, B 2, …, BN ¨ Each advertiser provides bids for keywords he is interested in. queries (online) Search Engine Select one Ad Advertiser pays his bid

The Adwords Problem: N advertisers; ¨ Daily Budgets B 1, B 2, …, BN ¨ Each advertiser provides bids for keywords he is interested in. queries (online) Search Engine Select one Ad Advertiser pays his bid Maximize total revenue Online competitive analysis - compare with best offline allocation

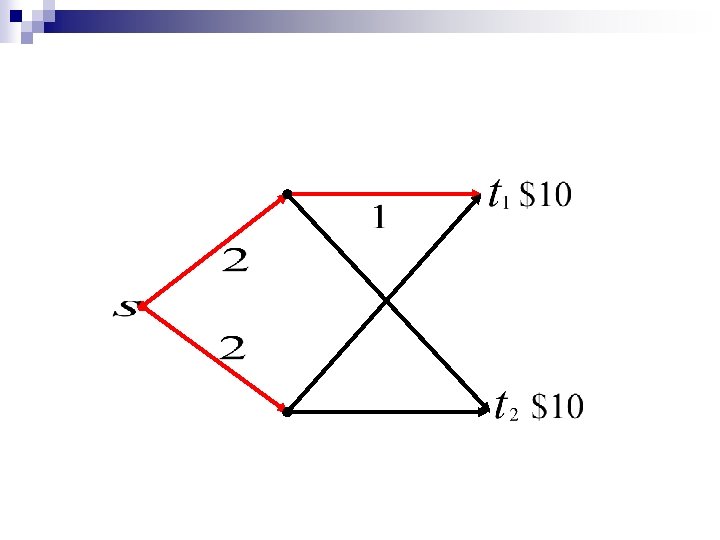
The Adwords Problem: N advertisers; ¨ Daily Budgets B 1, B 2, …, BN ¨ Each advertiser provides bids for keywords he is interested in. queries (online) Search Engine Select one Ad Advertiser pays his bid Maximize total revenue Example – Assign to highest bidder: only ½ the offline revenue

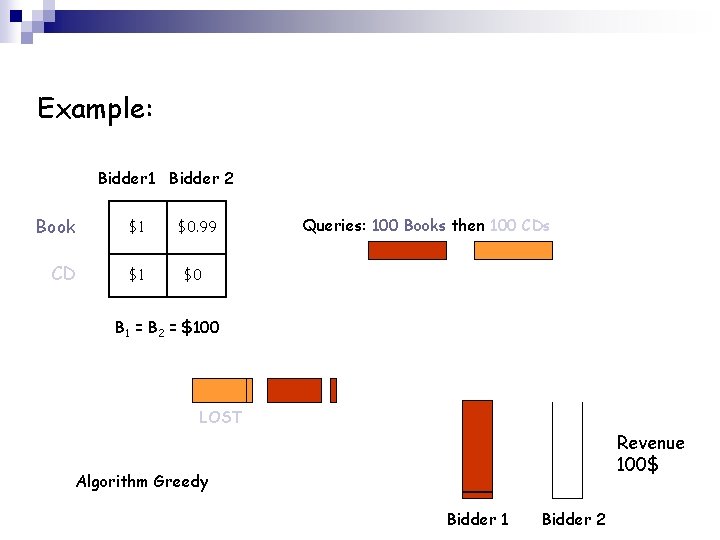
Example: Bidder 1 Bidder 2 Book $1 CD $1 $0. 99 Queries: 100 Books then 100 CDs $0 B 1 = B 2 = $100 LOST Revenue 100$ Algorithm Greedy Bidder 1 Bidder 2

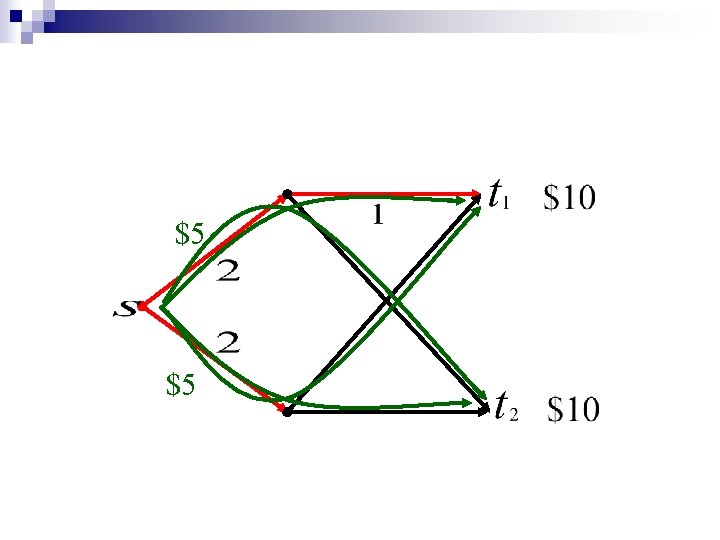
Example: Bidder 1 Bidder 2 Book $1 CD $1 $0. 99 Queries: 100 Books then 100 CDs $0 B 1 = B 2 = $100 Revenue 199$ Optimal Allocation Bidder 1 Bidder 2

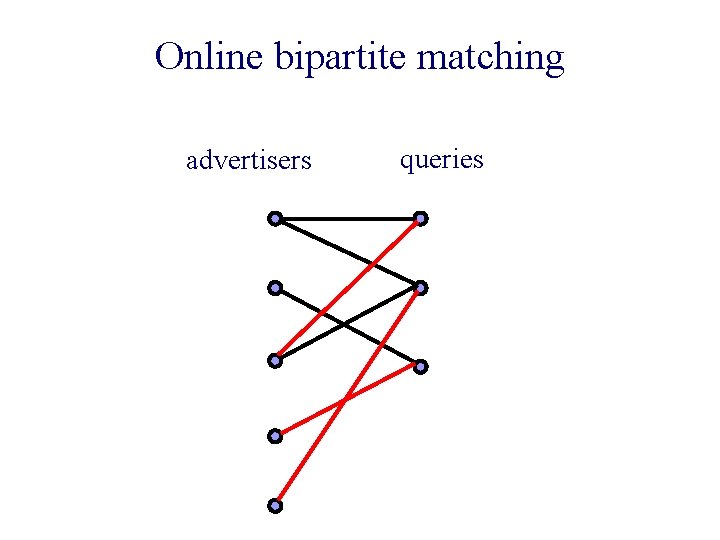
Generalizes online bipartite matching n Each daily budget is $1, and each bid is $0/1.

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching advertisers queries

Online bipartite matching n Karp, Vazirani & Vazirani, 1990: 1 -1/e factor randomized algorithm.

Online bipartite matching n Karp, Vazirani & Vazirani, 1990: 1 -1/e factor randomized algorithm. Optimal!

Online bipartite matching n Karp, Vazirani & Vazirani, 1990: 1 -1/e factor randomized algorithm. Optimal! n Kalyanasundaram & Pruhs, 1996: 1 -1/e factor algorithm for b-matching: Daily budgets $b, bids $0/1, b>>1

Adwords Problem n Mehta, Saberi, Vazirani & Vazirani, 2005: 1 -1/e algorithm, assuming budgets>>bids.

Adwords Problem n Mehta, Saberi, Vazirani & Vazirani, 2005: 1 -1/e algorithm, assuming budgets>>bids. Optimal!

New Algorithmic Technique n Idea: Use both bid and fraction of left-over budget

New Algorithmic Technique n Idea: Use both bid and fraction of left-over budget n Correct tradeoff given by tradeoff-revealing family of LP’s

Historically, the study of markets n has been of central importance, especially in the West

A Capitalistic Economy depends crucially on pricing mechanisms, with very little intervention, to ensure: Stability n Efficiency n Fairness n

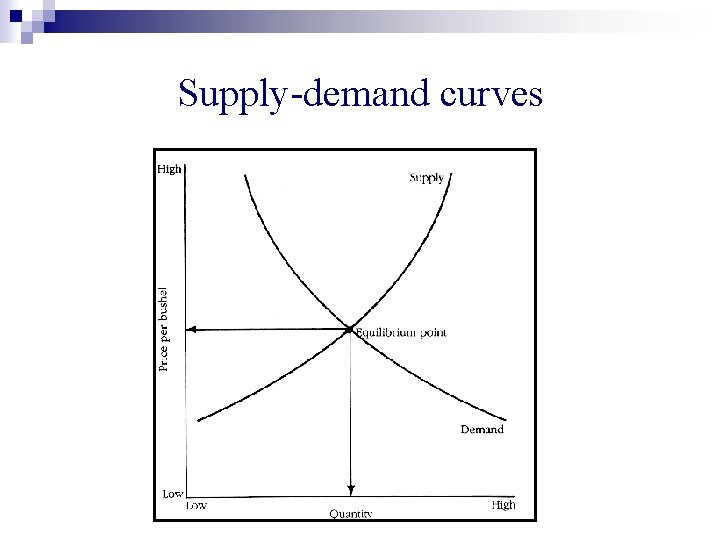
Do markets even have inherently stable operating points?

Do markets even have inherently stable operating points? General Equilibrium Theory Occupied center stage in Mathematical Economics for over a century

Leon Walras, 1874 n Pioneered general equilibrium theory

Supply-demand curves

Irving Fisher, 1891 n Fundamental market model

Fisher’s Model, 1891 $ $$$$$ ¢ wine bread cheese n milk $$$$ People want to maximize happiness – assume Findutilities. prices s. t. market clears linear

Fisher’s Model n n n buyers, with specified money, m(i) for buyer i k goods (unit amount of each good) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i,

Fisher’s Model n n n buyers, with specified money, m(i) k goods (each unit amount, w. l. o. g. ) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i, Find prices s. t. market clears, i. e. , all goods sold, all money spent.


Arrow-Debreu Theorem, 1954 n Celebrated theorem in Mathematical Economics n Established existence of market equilibrium under very general conditions using a deep theorem from topology - Kakutani fixed point theorem.

Kenneth Arrow n Nobel Prize, 1972

Gerard Debreu n Nobel Prize, 1983

Arrow-Debreu Theorem, 1954. n Highly non-constructive

Adam Smith n The Wealth of Nations 2 volumes, 1776. n ‘invisible hand’ of the market

What is needed today? n An inherently algorithmic theory of market equilibrium n New models that capture new markets

n Beginnings of such a theory, within Algorithmic Game Theory n Started with combinatorial algorithms for traditional market models n New market models emerging

Combinatorial Algorithm for Fisher’s Model n Devanur, Papadimitriou, Saberi & V. , 2002 Using primal-dual schema

Primal-Dual Schema n Highly successful algorithm design technique from exact and approximation algorithms

Exact Algorithms for Cornerstone Problems in P: n n n Matching (general graph) Network flow Shortest paths Minimum spanning tree Minimum branching

Approximation Algorithms set cover Steiner tree Steiner network k-MST scheduling. . . facility location k-median multicut feedback vertex set

n No LP’s known for capturing equilibrium allocations for Fisher’s model n Eisenberg-Gale convex program, 1959 n DPSV: Extended primal-dual schema to solving nonlinear convex programs

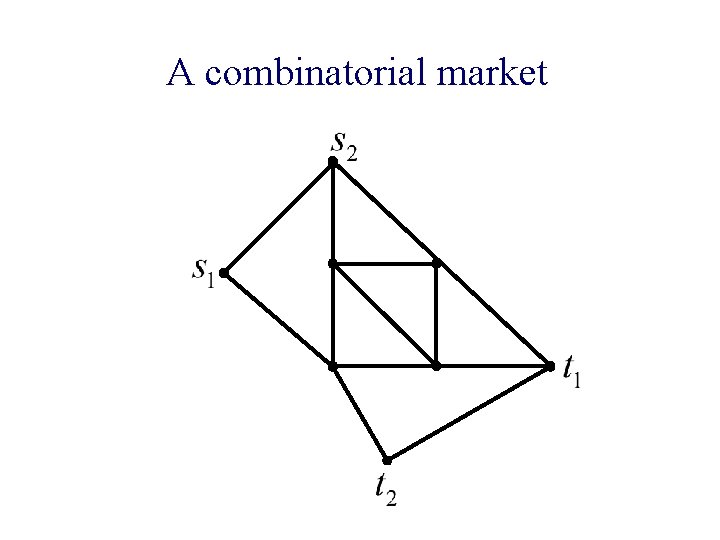
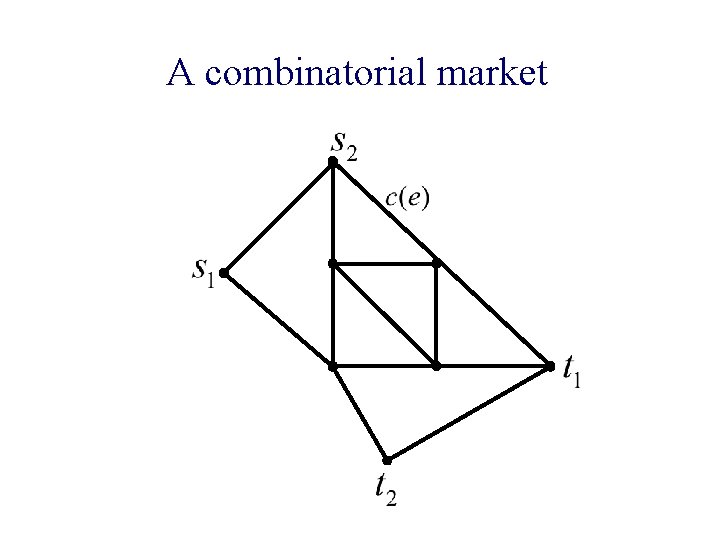
A combinatorial market

A combinatorial market

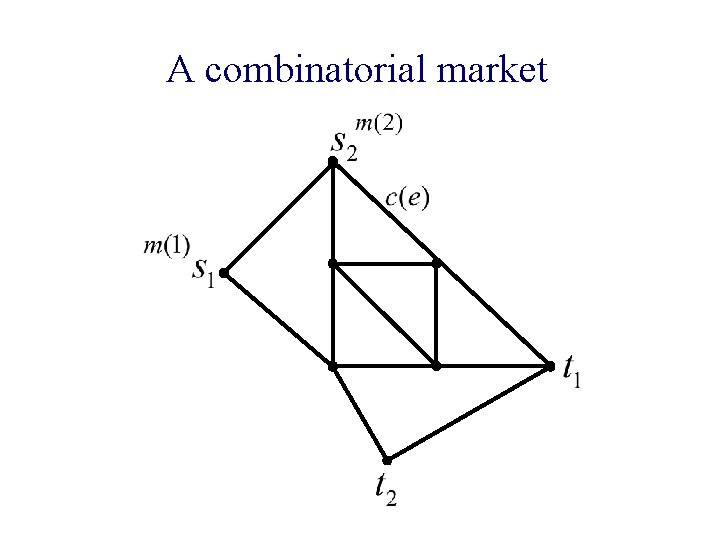
A combinatorial market

A combinatorial market n Given: ¨ Network G = (V, E) (directed or undirected) ¨ Capacities on edges c(e) ¨ Agents: source-sink pairs with money m(1), … m(k) n Find: equilibrium flows and edge prices

Equilibrium n Flows and edge prices f(i): flow of agent i ¨ p(e): price/unit flow of edge e ¨ n Satisfying: p(e)>0 only if e is saturated ¨ flows go on cheapest paths ¨ money of each agent is fully spent ¨

Kelly’s resource allocation model, 1997 Mathematical framework for understanding TCP congestion control Highly successful theory

TCP Congestion Control f(i): source rate n p(e): prob. of packet loss (in TCP Reno) queueing delay (in TCP Vegas) n

TCP Congestion Control n n f(i): source rate p(e): prob. of packet loss (in TCP Reno) queueing delay (in TCP Vegas) Kelly: Equilibrium flows are proportionally fair: only way of adding 5% flow to someone’s dollar is to decrease 5% flow from someone else’s dollar.

TCP Congestion Control primal process: packet rates at sources dual process: packet drop at links AIMD + RED converges to equilibrium in the limit

n Kelly & V. , 2002: Kelly’s model is a generalization of Fisher’s model. n Find combinatorial polynomial time algorithms!

Jain & V. , 2005: n Strongly polynomial combinatorial algorithm for single-source multiple-sink market

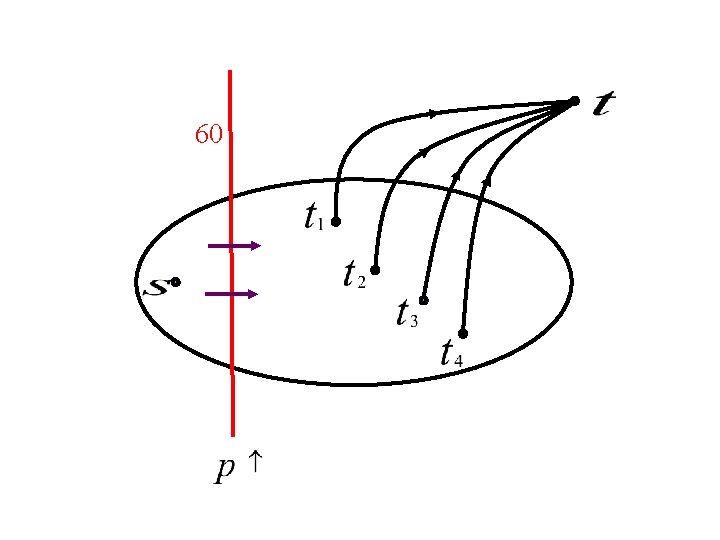
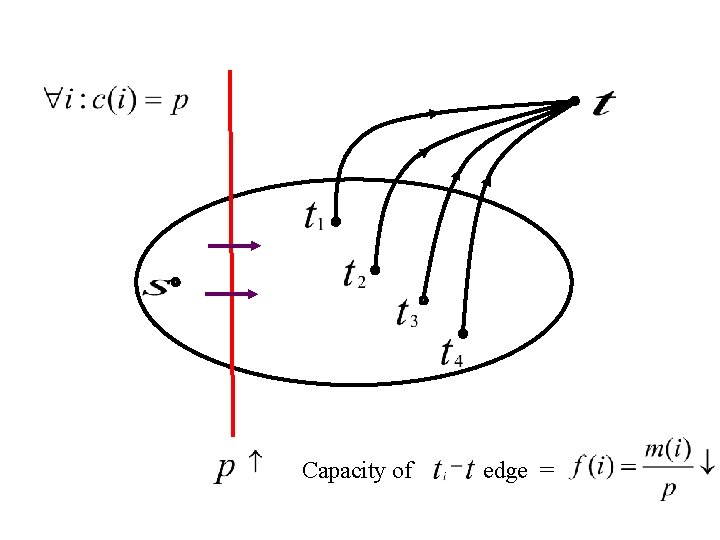
Single-source multiple-sink market n Given: ¨ Network G = (V, E), s: source ¨ Capacities on edges c(e) ¨ Agents: sinks with money m(1), … m(k) n Find: equilibrium flows and edge prices

Equilibrium n Flows and edge prices f(i): flow of agent i ¨ p(e): price/unit flow of edge e ¨ n Satisfying: p(e)>0 only if e is saturated ¨ flows go on cheapest paths ¨ money of each agent is fully spent ¨


$5 $5


$30 $10 $40

Jain & V. , 2005: n Strongly polynomial combinatorial algorithm for single-source multiple-sink market n Ascending price auction ¨ Buyers: sinks (fixed budgets, maximize flow) ¨ Sellers: edges (maximize price)

Auction of k identical goods p = 0; n while there are >k buyers: raise p; n end; n sell to remaining k buyers at price p; n

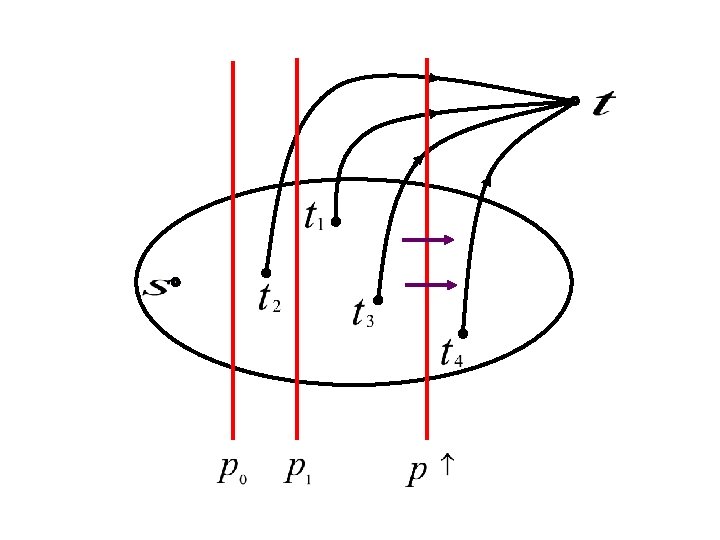
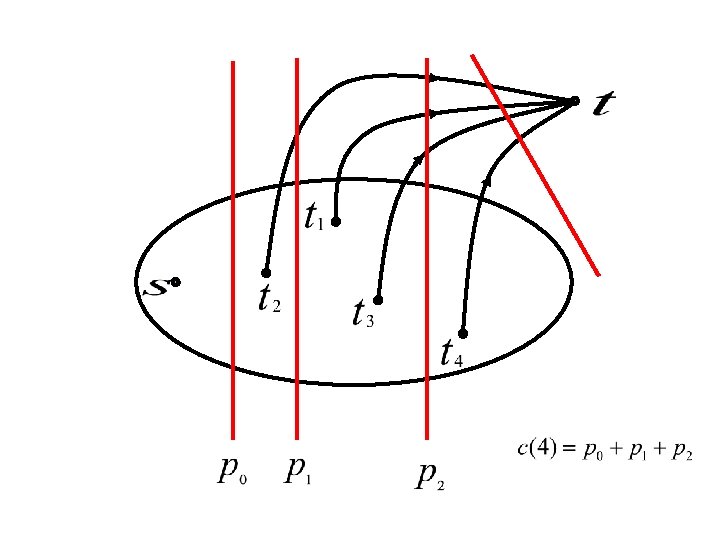
Find equilibrium prices and flows

Find equilibrium prices and flows m(1) cap(e) m(2) m(3) m(4)

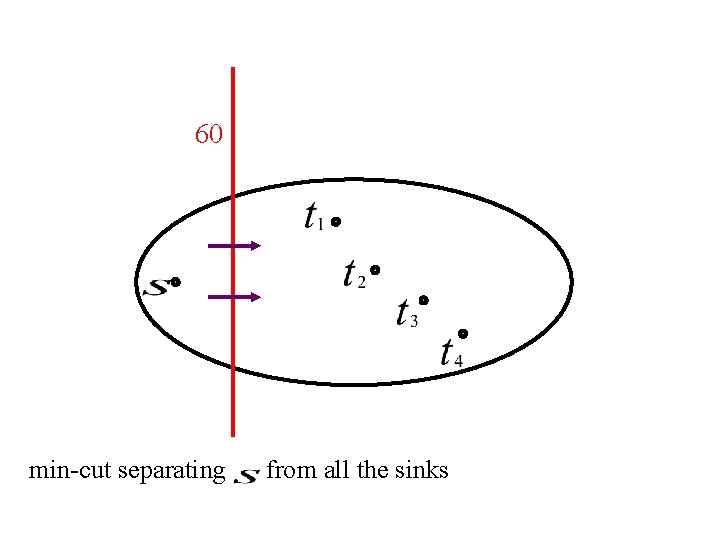
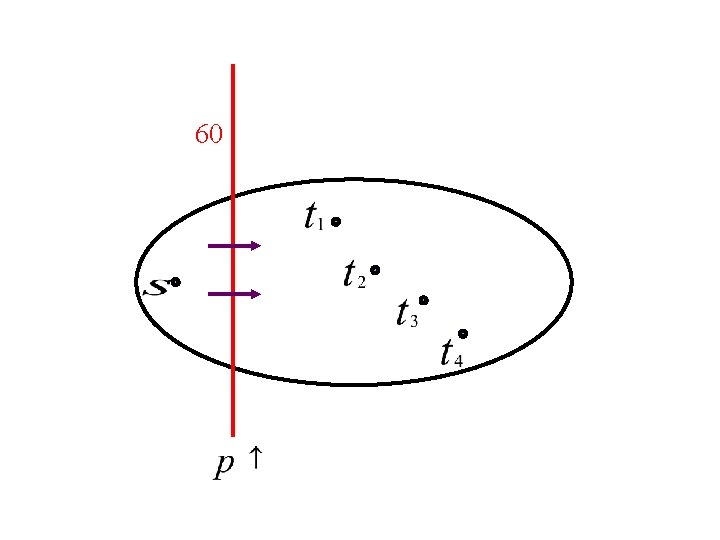
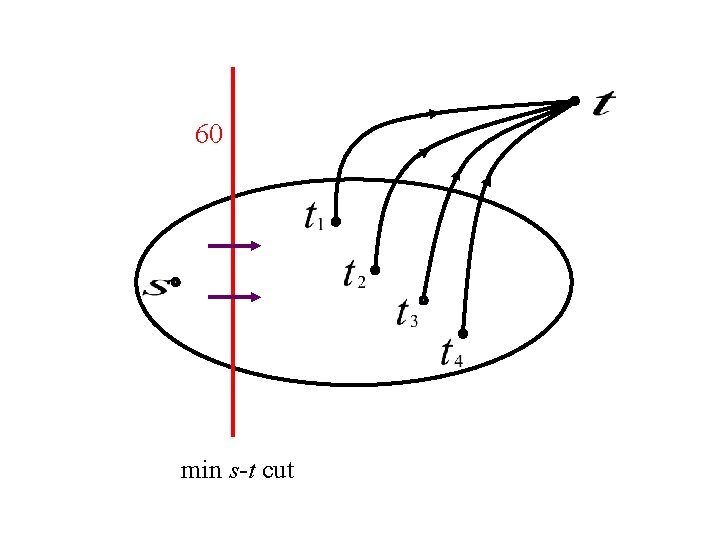
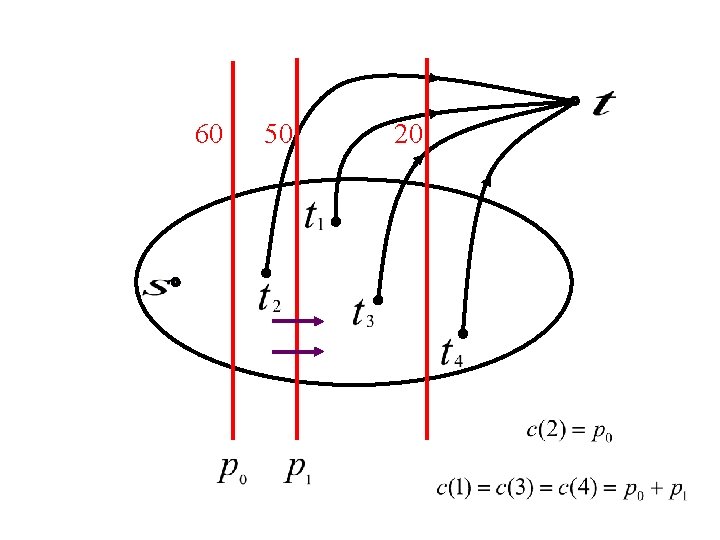
60 min-cut separating from all the sinks

60

60

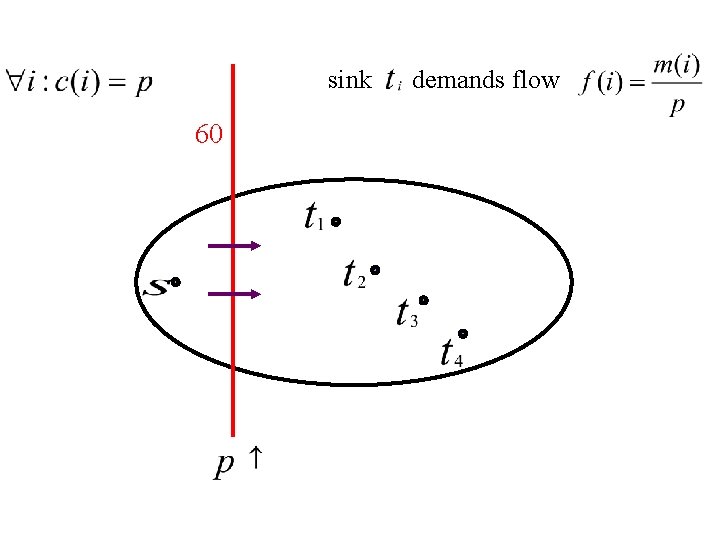
Throughout the algorithm: c(i): cost of cheapest path from sink demands flow to

sink 60 demands flow

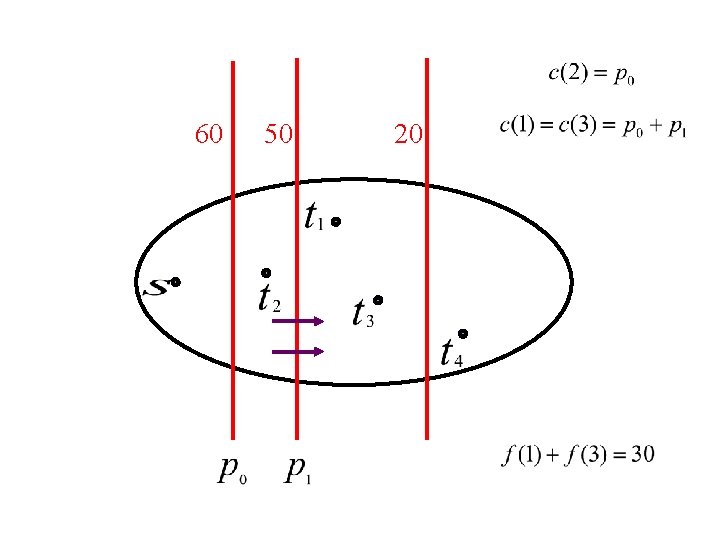
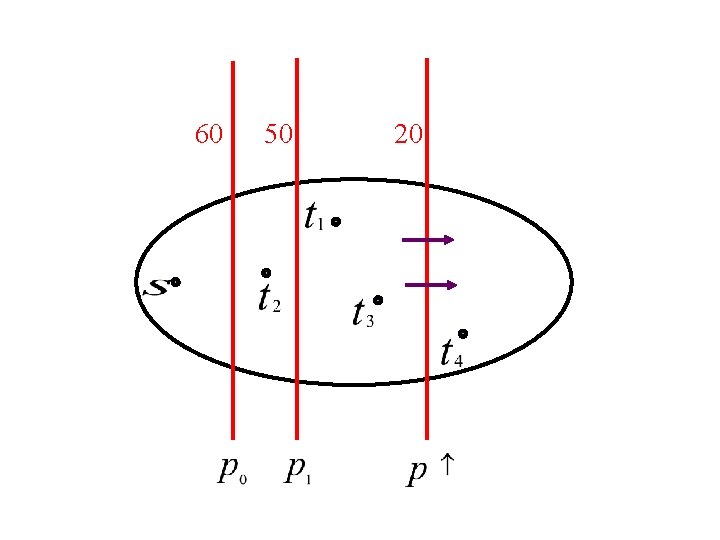
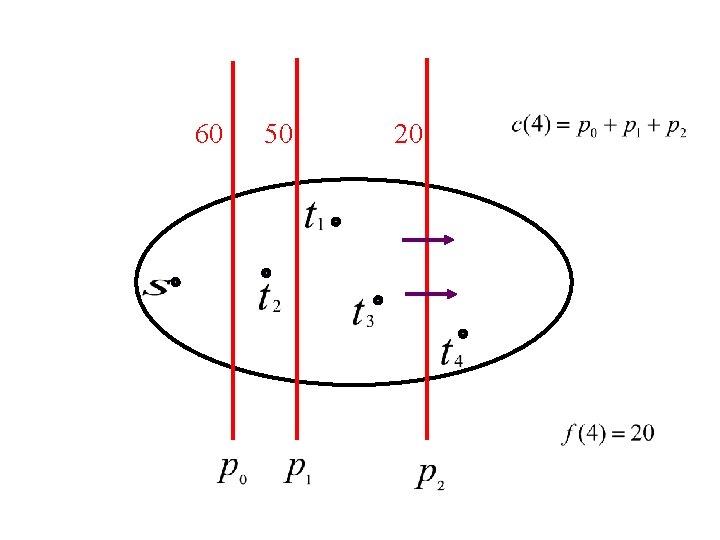
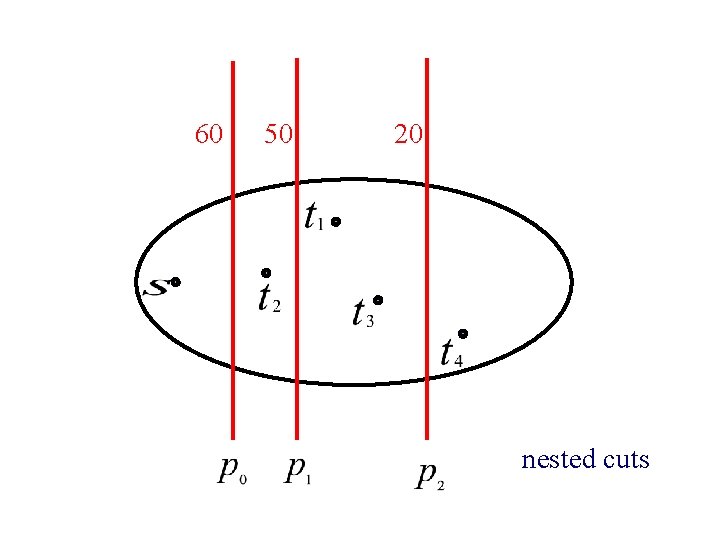
Auction of edges in cut p = 0; n while the cut is over-saturated: raise p; n end; n assign price p to all edges in the cut; n

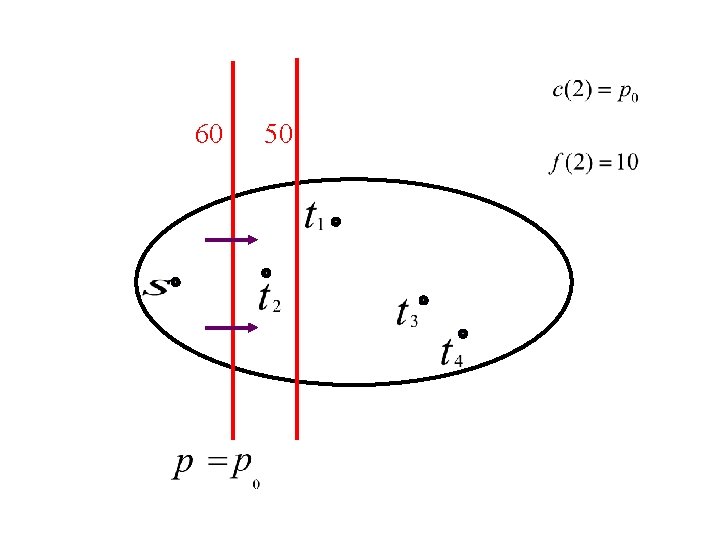
60 50

60 50

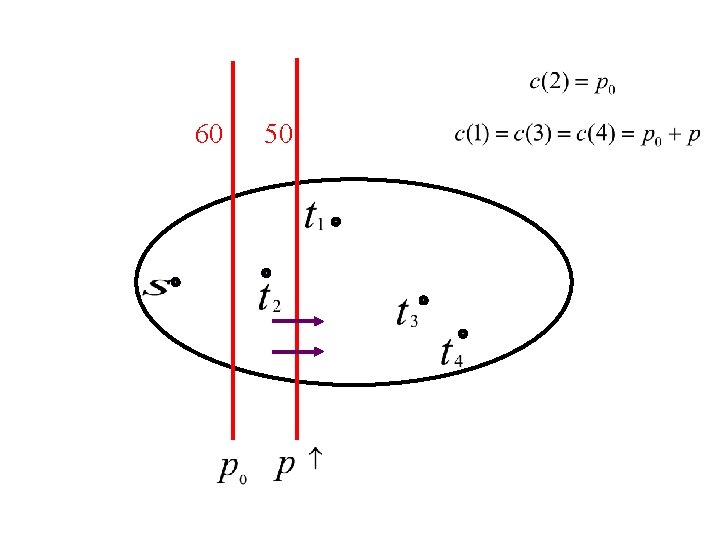
60 50 20

60 50 20

60 50 20

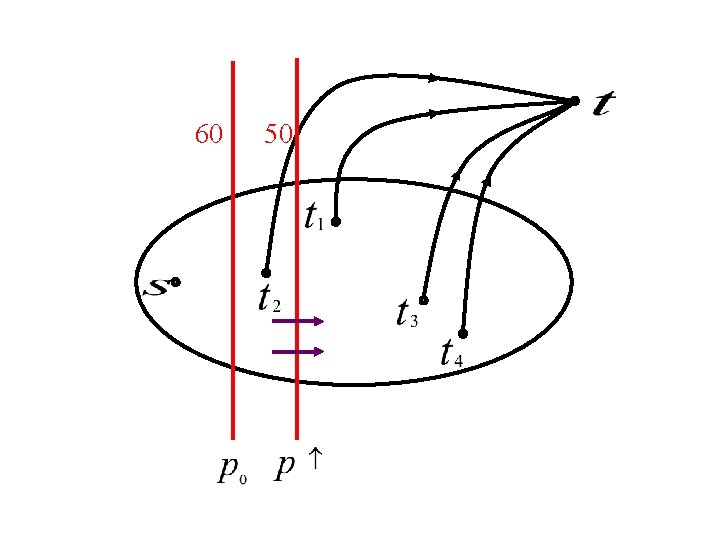
60 50 20 nested cuts

n Flow and prices will: ¨ Saturate all red cuts ¨ Use up sinks’ money ¨ Send flow on cheapest paths

Implementation


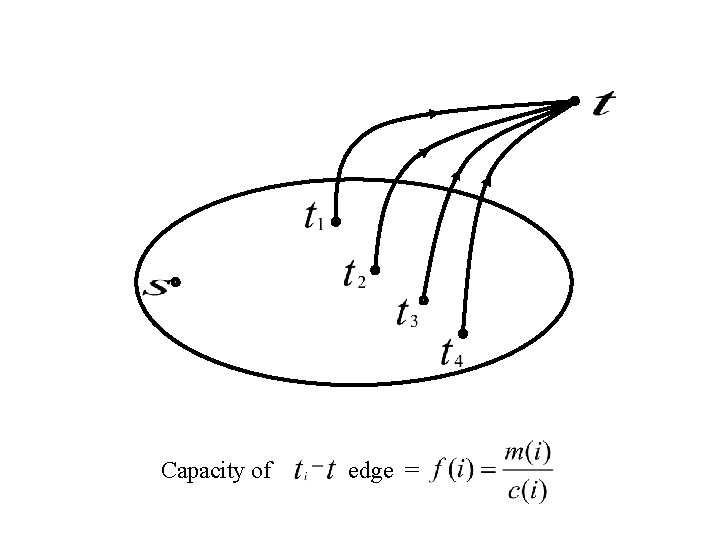
Capacity of edge =

60 min s-t cut

60

60

Capacity of edge =

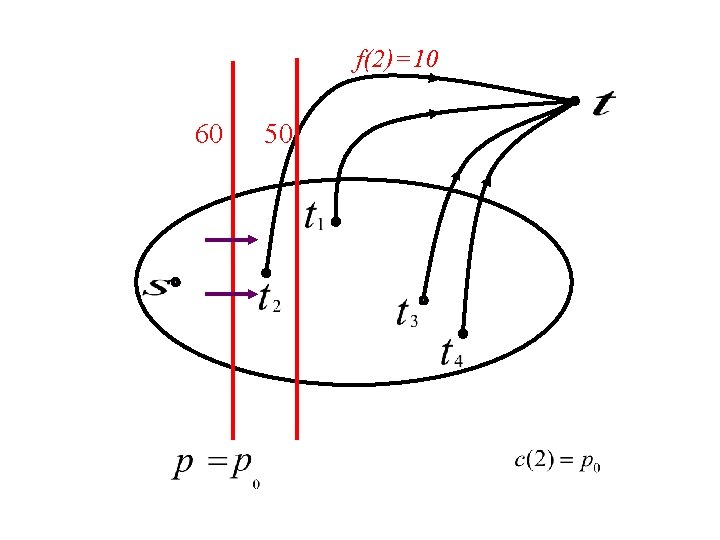
f(2)=10 60 50

60 50

60 50 20


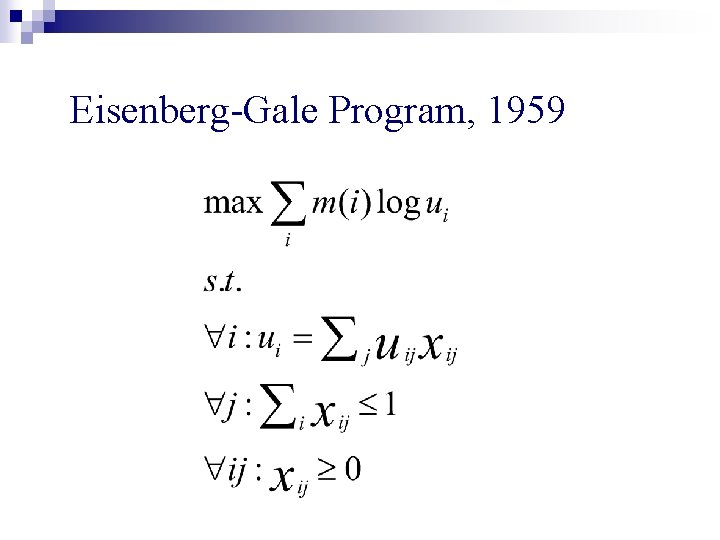
Eisenberg-Gale Program, 1959

n Lagrangian variables: prices of goods n Using KKT conditions: optimal primal and dual solutions are in equilibrium

Convex Program for Kelly’s Model

JV Algorithm n primal-dual alg. for nonlinear convex program n “primal” variables: flows n “dual” variables: prices of edges n algorithm: primal & dual improvements Allocations Prices

Rational!!

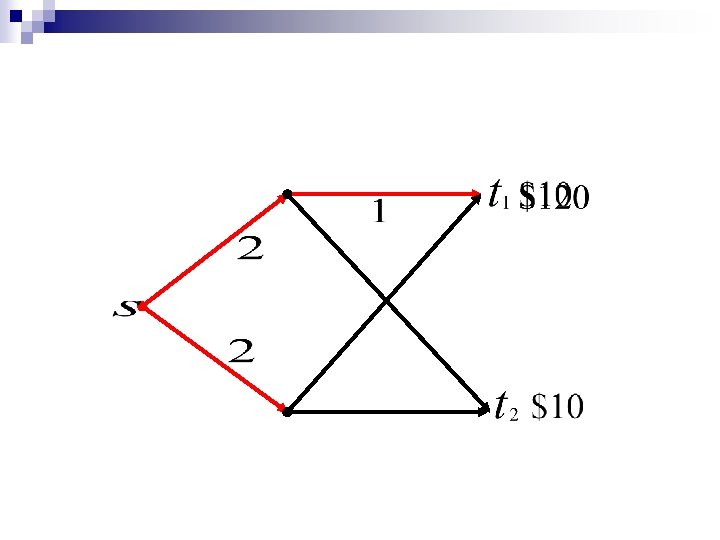
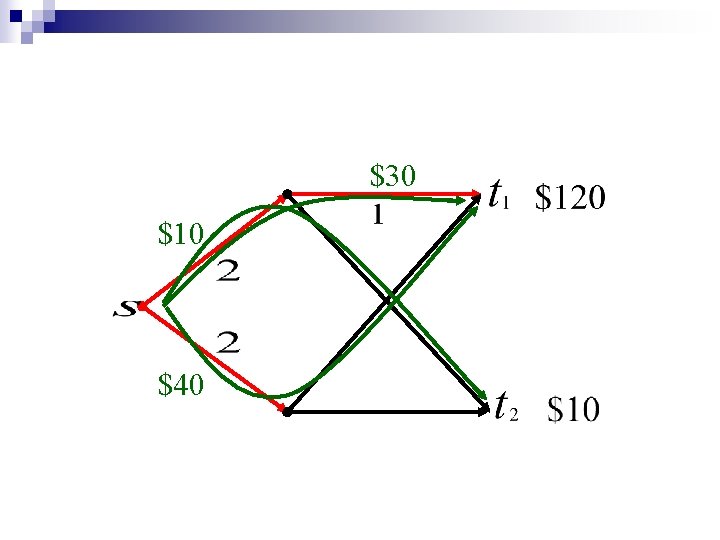
Irrational for 2 sources & 3 sinks $1 $1 $1

Irrational for 2 sources & 3 sinks Equilibrium prices

Max-flow min-cut theorem!

Other resource allocation markets 2 source-sink pairs (directed/undirected) n Branchings rooted at sources (agents) n

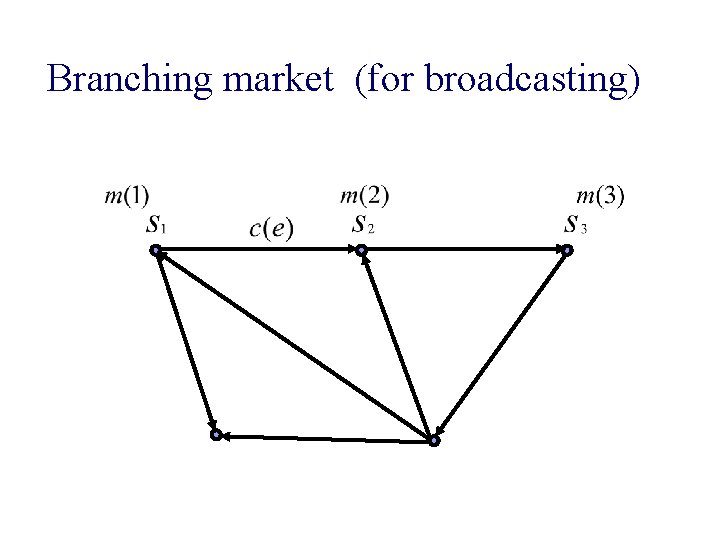
Branching market (for broadcasting)

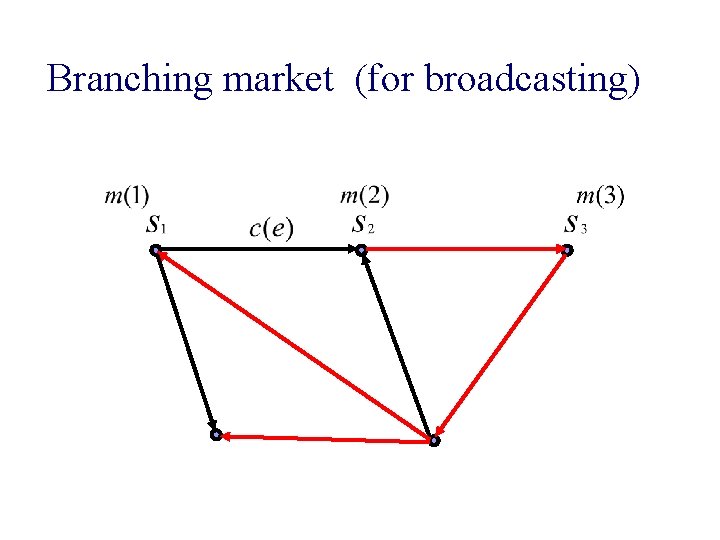
Branching market (for broadcasting)

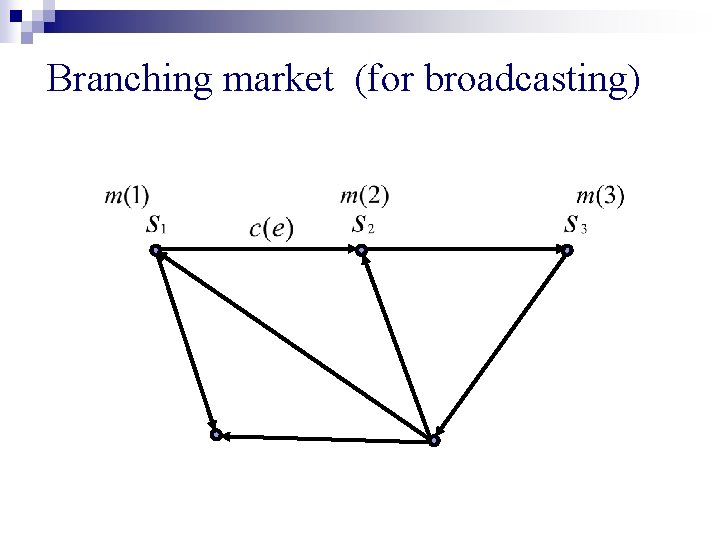
Branching market (for broadcasting)

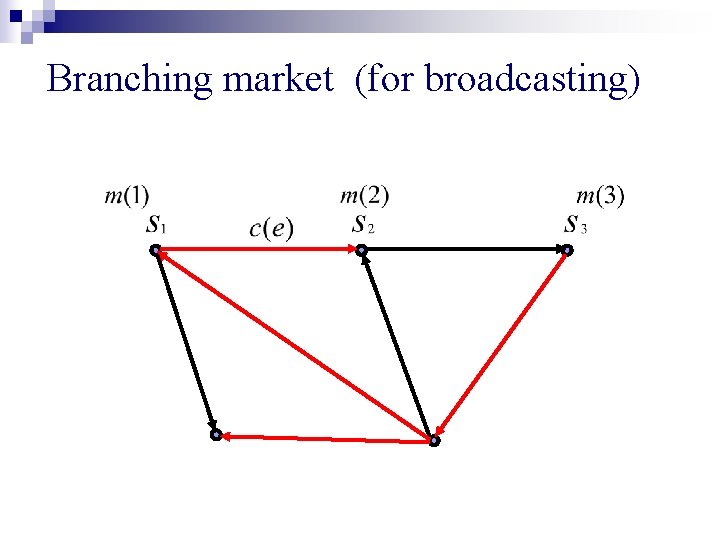
Branching market (for broadcasting)

Branching market (for broadcasting) n Given: Network G = (V, E), directed ¨ edge capacities ¨ sources, ¨ money of each source n Find: edge prices and a packing of branchings rooted at sources s. t. p(e) > 0 => e is saturated ¨ each branching is cheapest possible ¨ money of each source fully used. ¨

Eisenberg-Gale-type program for branching market s. t. packing of branchings

Other resource allocation markets 2 source-sink pairs (directed/undirected) n Branchings rooted at sources (agents) n Spanning trees n Network coding n

Eisenberg-Gale-Type Convex Program s. t. packing constraints

Eisenberg-Gale Market n A market whose equilibrium is captured as an optimal solution to an Eisenberg-Gale-type program

n Theorem: Strongly polynomial algs for following markets : ¨ 2 source-sink pairs, undirected (Hu, 1963) ¨ spanning tree (Nash-William & Tutte, 1961) ¨ 2 sources branching (Edmonds, 1967 + JV, 2005) n 3 sources branching: irrational

n Theorem: Strongly polynomial algs for following markets : ¨ 2 source-sink pairs, undirected (Hu, 1963) ¨ spanning tree (Nash-William & Tutte, 1961) ¨ 2 sources branching (Edmonds, 1967 + JV, 2005) n 3 sources branching: irrational n Open: (no max-min theorems): ¨ 2 source-sink pairs, directed ¨ 2 sources, network coding
![Chakrabarty Devanur V 2006 n EG2 EisenbergGale markets with 2 agents n Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-127.jpg)
Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n Theorem: EG[2] markets are rational.
![Chakrabarty Devanur V 2006 n EG2 EisenbergGale markets with 2 agents n Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-128.jpg)
Chakrabarty, Devanur & V. , 2006: n EG[2]: Eisenberg-Gale markets with 2 agents n Theorem: EG[2] markets are rational. n Combinatorial EG[2] markets: polytope of feasible utilities can be described via combinatorial LP. n Theorem: Strongly poly alg for Comb EG[2].
![3 source branching Singlesource 2 ss undir SUA Comb EG2 2 ss dir Fisher 3 -source branching Single-source 2 s-s undir SUA Comb EG[2] 2 s-s dir Fisher](https://slidetodoc.com/presentation_image_h2/a32aeff75baeb09e8449da0ced3d5eef/image-129.jpg)
3 -source branching Single-source 2 s-s undir SUA Comb EG[2] 2 s-s dir Fisher EG[2] EG Rational

Efficiency of Markets ‘‘price of capitalism’’ n Agents: n ¨ different abilities to control prices ¨ idiosyncratic ways of utilizing resources n Q: Overall output of market when forced to operate at equilibrium?

Efficiency

Efficiency n Rich classification!

Market Efficiency Single-source 1 3 -source branching k source-sink undirected 2 source-sink directed arbitrarily small

Other properties: Fairness (max-min + min-max fair) n Competition monotonicity n

Open issues n Strongly poly algs for approximating ¨ nonlinear convex programs ¨ equilibria n Insights into congestion control protocols?


