Prerequisites Almost essential Game Theory Dynamic REPEATED GAMES

Prerequisites Almost essential Game Theory: Dynamic REPEATED GAMES MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell: Repeated Games 1

Overview Repeated Games Basic structure Embedding the game in context Equilibrium issues Applications April 2018 Frank Cowell: Repeated Games 2

Introduction § Another examination of the role of time § Dynamic analysis can be difficult • more than a few stages • can lead to complicated analysis of equilibrium § We need an alternative approach • one that preserves basic insights of dynamic games • for example, subgame-perfect equilibrium § Build on the idea of dynamic games • introduce a jump • move from the case of comparatively few stages • to the case of arbitrarily many April 2018 Frank Cowell: Repeated Games 3

Repeated games § The alternative approach • take a series of the same game • embed it within a time-line structure § Basic idea is simple • connect multiple instances of an atemporal game • model a repeated encounter between the players in the same situation of economic conflict § Raises important questions • how does this structure differ from an atemporal model? • how does the repetition of a game differ from a single play? • how does it differ from a collection of unrelated games of identical structure with identical players? April 2018 Frank Cowell: Repeated Games 4

History § Why is the time-line different from a collection of unrelated games? § The key is history • consider history at any point on the timeline • contains information about actual play • information accumulated up to that point § History can affect the nature of the game • at any stage all players can know all the accumulated information • strategies can be conditioned on this information § History can play a role in the equilibrium • some interesting outcomes aren’t equilibria in a single encounter • these may be equilibrium outcomes in the repeated game • the game’s history is used to support such outcomes April 2018 Frank Cowell: Repeated Games 5

Repeated games: Structure § The stage game • take an instant in time • specify a simultaneous-move game • payoffs completely specified by actions within the game § Repeat the stage game indefinitely • there’s an instance of the stage game at time 0, 1, 2, …, t, … • the possible payoffs are also repeated for each t • payoffs at t depends on actions in stage game at t § A modified strategic environment • all previous actions assumed as common knowledge • so agents’ strategies can be conditioned on this information § Modifies equilibrium behaviour and outcome? April 2018 Frank Cowell: Repeated Games 6

Equilibrium § Simplified structure has potential advantages • whether significant depends on nature of stage game • concern nature of equilibrium § Possibilities for equilibrium • new strategy combinations supportable as equilibria? • long-term cooperative outcomes • absent from a myopic analysis of a simple game § Refinements of subgame perfection simplify the analysis: • can rule out empty threats • and incredible promises • disregard irrelevant “might-have-beens” April 2018 Frank Cowell: Repeated Games 7

Overview Repeated Games Basic structure Developing the basic concepts Equilibrium issues Applications April 2018 Frank Cowell: Repeated Games 8

Equilibrium: an approach § Focus on key question in repeated games: • how can rational players use the information from history? • need to address this to characterise equilibrium § Illustrate a method in an argument by example • outline for the Prisoner's Dilemma game • same players face same outcomes from their actions that they may choose in periods 1, 2, …, t, … § Prisoner's Dilemma particularly instructive given: • its importance in microeconomics • pessimistic outcome of an isolated round of the game April 2018 Frank Cowell: Repeated Games 9

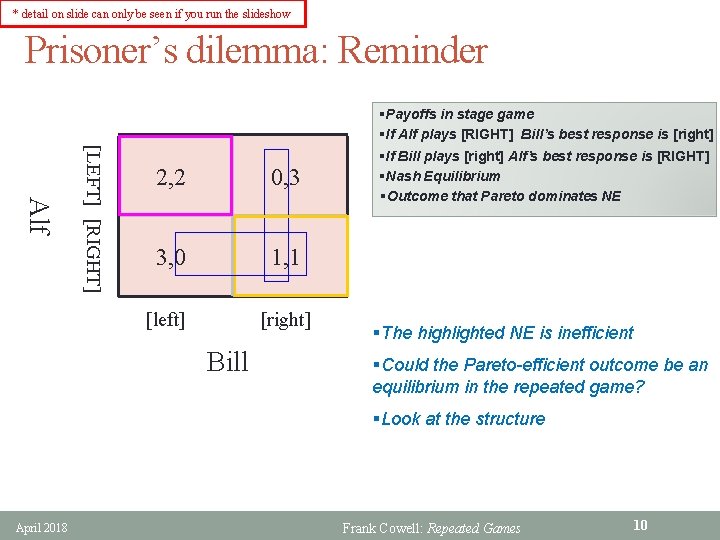
* detail on slide can only be seen if you run the slideshow Prisoner’s dilemma: Reminder §Payoffs in stage game §If Alf plays [RIGHT] Bill’s best response is [right] [LEFT] [RIGHT] Alf 2, 2 0, 3 3, 0 1, 1 [left] [right] Bill §If Bill plays [right] Alf’s best response is [RIGHT] §Nash Equilibrium §Outcome that Pareto dominates NE §The highlighted NE is inefficient §Could the Pareto-efficient outcome be an equilibrium in the repeated game? §Look at the structure April 2018 Frank Cowell: Repeated Games 10

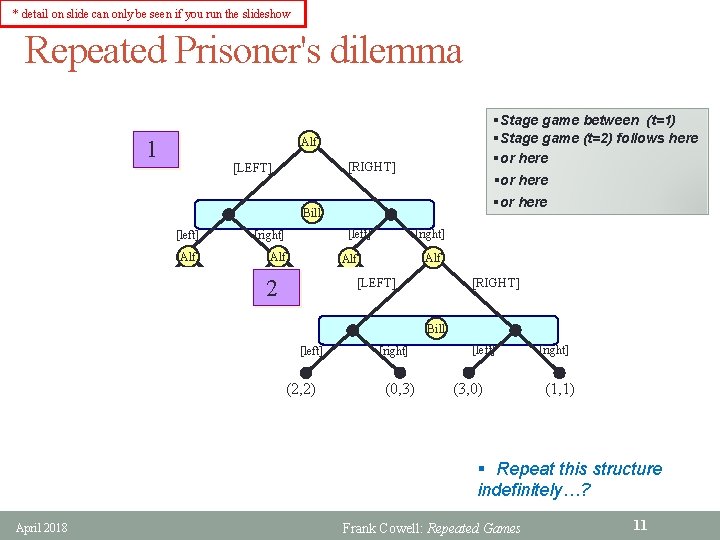
* detail on slide can only be seen if you run the slideshow Repeated Prisoner's dilemma §Stage game between (t=1) §Stage game (t=2) follows here §or here Alf 1 [RIGHT] [LEFT] §or here Bill 2 2 [LEFT] [right] Alf (2, 2) 2 (2, 2) [right] Alf (0, 3) (3, 0) Bill (1, 1) [RIGHT][LEFT] [RIGHT] [LEFT] 2 Bill [left] [right] [left] (0, 3) (2, 2) (3, 0) (0, 3) (2, 2) [right] [left] (1, 1) (3, 0) (2, 2) (0, 3) [RIGHT] Bill [right] [left] [right] (1, 1) (0, 3) (3, 0) (1, 1) (3, 0) [right] (1, 1) § Repeat this structure indefinitely…? April 2018 Frank Cowell: Repeated Games 11

Repeated Prisoner's dilemma §The stage game Alf 1 §repeated though time [RIGHT] [LEFT] Bill [left] (2, 2) [left] [right] … … (0, 3) (3, 0) [right] … (1, 1) Alf t [RIGHT] [LEFT] Bill [left] (2, 2) April 2018 [right] … (0, 3) [left] … (3, 0) [right] Let's look at the detail … (1, 1) Frank Cowell: Repeated Games 12

Repeated PD: payoffs § To represent possibilities in long run: • first consider payoffs available in the stage game • then those available through mixtures § In the one-shot game payoffs simply represented • it was enough to denote them as 0, …, 3 • purely ordinal • arbitrary monotonic changes of the payoffs have no effect § Now we need a generalised notation • cardinal values of utility matter • we need to sum utilities, compare utility differences § Evaluation of a payoff stream: • suppose payoff to agent h in period t is uh(t) • value of (uh(1), uh(2), …, uh(t)…) is given by ∞ [1 d] ∑ dt 1 uh(t) t=1 • April 2018 where d is a discount factor 0 < d < 1 Frank Cowell: Repeated Games 13

PD: stage game § A generalised notation for the stage game • consider actions and payoffs • in each of four fundamental cases § Both socially irresponsible: • they play [RIGHT], [right] • get ( ua, ub) where ua > 0, ub > 0 § Both socially responsible: • they play [LEFT], [left] • get (u*a, u*b) where u*a > ua, u*b > ub § Only Alf socially responsible: • they play [LEFT], [right] • get ( 0, ub) where ub > u*b § Only Bill socially responsible: • they play [RIGHT], [left] • get ( ua, 0) where ua > u*a April 2018 A diagrammatic view Frank Cowell: Repeated Games 14

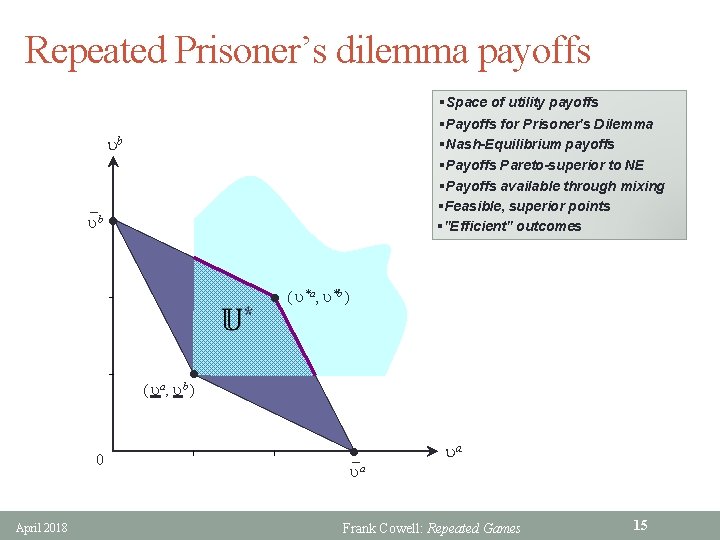
Repeated Prisoner’s dilemma payoffs §Space of utility payoffs §Payoffs for Prisoner's Dilemma §Nash-Equilibrium payoffs §Payoffs Pareto-superior to NE §Payoffs available through mixing §Feasible, superior points §"Efficient" outcomes ub _ ub • • (u *a, u*b ) • ( ua, ub ) 0 April 2018 • u_ ua a Frank Cowell: Repeated Games 15

Choosing a strategy: setting § Long-run advantage in the Pareto-efficient outcome • payoffs (u*a, u*b) in each period • clearly better than ( ua, ub) in each period § Suppose the agents recognise the advantage • what actions would guarantee them this? • clearly they need to play [LEFT], [left] every period § The problem is lack of trust: • they cannot trust each other • nor indeed themselves: • Alf tempted to be antisocial and get payoff ua by playing [RIGHT] • Bill has a similar temptation April 2018 Frank Cowell: Repeated Games 16

Choosing a strategy: formulation § Will a dominated outcome still be inevitable? § Suppose each player adopts a strategy that 1. rewards the other party's responsible behaviour by responding with the action [left] 2. punishes antisocial behaviour with the action [right], thus generating the minimax payoffs (ua, ub) § Known as a trigger strategy § Why the strategy is powerful • punishment applies to every period after the one where the antisocial action occurred • if punishment invoked offender is “minimaxed for ever” § Look at it in detail April 2018 Frank Cowell: Repeated Games 17

Repeated PD: trigger strategies Bill’s action in 0, …, t s. T a Alf’s action at t+1 [LEFT] [left], …, [left] [RIGHT] Anything else §Take situation at t §First type of history §Response of other player to continue this history §Second type of history §Punishment response §Trigger strategies [s. Ta, s. Tb] Alf’s action in 0, …, t s. T b [LEFT], …, [LEFT] Anything else April 2018 Bill’s action at t+1 [left] Will it work? [right] Frank Cowell: Repeated Games 18

Will the trigger strategy “work”? § Utility gain from “misbehaving” at t: ua − u*a § What is value at t of punishment from t + 1 onwards? • Difference in utility period: u*a − ua • Discounted value of this in period t + 1: V : = [u*a − ua]/[1 −d ] • Value of this in period t: d. V = d[u*a − ua]/[1 −d ] § So agent chooses not to misbehave if • ua − u*a ≤ d[u*a − ua ]/[1 −d ] § But this is only going to work for specific parameters • value of d • relative to ua, ua and u*a § What values of discount factor will allow an equilibrium? April 2018 Frank Cowell: Repeated Games 19

Discounting and equilibrium § For an equilibrium condition must be satisfied for both a and b § Consider the situation of a § Rearranging the condition from the previous slide: • d[u*a − ua ] ≥ [1 −d] [ ua − u*a ] • d[ ua − ua ] ≥ [ ua − u*a ] § Simplifying this the condition must be • d ≥ da • where da : = [ ua − u*a ] / [ ua − ua ] § A similar result must also apply to agent b § Therefore we must have the condition: • d≥d • where d : = max {da , db} April 2018 Frank Cowell: Repeated Games 20

Repeated PD: SPNE § Assuming d ≥ d, take the strategies [s. Ta, s. Tb] prescribed by the Table § If there were antisocial behaviour at t consider subgame that would start at t + 1 • Alf could not increase his payoff by switching from [RIGHT] to [LEFT], given that Bill is playing [left] • • a similar remark applies to Bill • likewise for any subgame starting after t + 1 so strategies imply a NE for this subgame § But if [LEFT], [left] has been played in every period up till t: • • • Alf would not wish to switch to [RIGHT] a similar remark applies to Bill again we have a NE § So, if d is large enough, [s. Ta, s. Tb] is a Subgame-Perfect Equilibrium • April 2018 yields the payoffs (u*a, u*b) in every period Frank Cowell: Repeated Games 21

Folk Theorem § The outcome of the repeated PD is instructive • illustrates an important result • the Folk Theorem § Strictly speaking a class of results • finite/infinite games • different types of equilibrium concepts § A standard version of the Theorem: • for a two-person infinitely repeated game: • suppose discount factor is sufficiently close to 1 • any combination of actions observed in any finite number of stages • this is the outcome of a subgame-perfect equilibrium April 2018 Frank Cowell: Repeated Games 22

Assessment § The Folk Theorem central to repeated games • perhaps better described as Folk Theorems • a class of results § Clearly has considerable attraction § Put its significance in context • makes relatively modest claims • gives a possibility result § Only seen one example of the Folk Theorem • let’s apply it • to well known oligopoly examples April 2018 Frank Cowell: Repeated Games 23

Overview Repeated Games Basic structure Some well-known examples Equilibrium issues Applications April 2018 Frank Cowell: Repeated Games 24

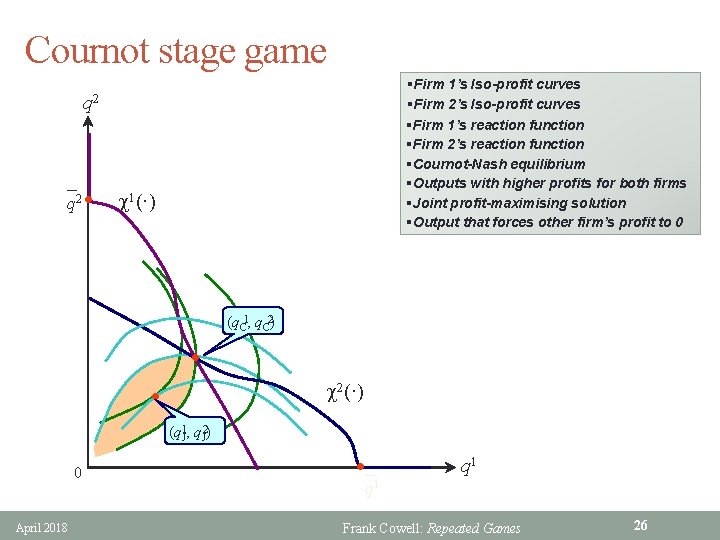
Cournot competition: repeated § Start by reinterpreting PD as Cournot duopoly • two identical firms • firms can each choose one of two levels of output – [high] or [low] • can firms sustain a low-output (i. e. high-profit) equilibrium? § Possible actions and outcomes in the stage game: • [HIGH], [high]: both firms get Cournot-Nash payoff PC > 0 • [LOW], [low]: both firms get joint-profit maximising payoff PJ > PC • [HIGH], [low]: payoffs are ( P, 0) where P > PJ § Folk theorem: get SPNE with payoffs (PJ, PJ) if d is large enough • Critical value for the discount factor d is P − PJ d = ────── P − PC § But we should say more • April 2018 Let’s review the standard Cournot diagram Frank Cowell: Repeated Games 25

Cournot stage game §Firm 1’s Iso-profit curves §Firm 2’s Iso-profit curves §Firm 1’s reaction function §Firm 2’s reaction function §Cournot-Nash equilibrium §Outputs with higher profits for both firms §Joint profit-maximising solution §Output that forces other firm’s profit to 0 q 2 l c 1(·) (q. C 1, q. C 2) l c 2(·) l (q 1 J, q. J 2) 0 April 2018 l q 1 Frank Cowell: Repeated Games 26

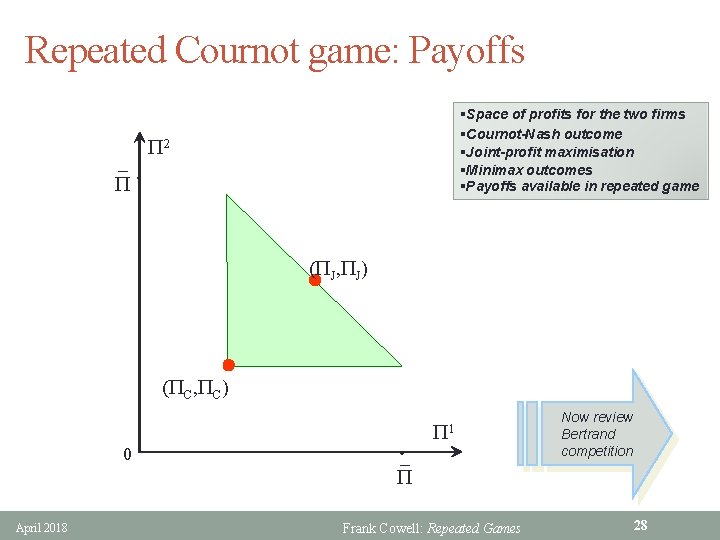
Repeated Cournot game: Punishment § Standard Cournot model is richer than simple PD: • action space for PD stage game just has the two output levels • continuum of output levels introduces further possibilities § Minimax profit level for firm 1 in a Cournot duopoly • is zero, not the NE outcome PC • arises where firm 2 sets output to q 2 such that 1 makes no profit § Imagine a deviation by firm 1 at time t • raises q 1 above joint profit-max level § Would minimax be used as punishment from t + 1 to ∞? • clearly (0, q 2) is not on firm 2's reaction function • so cannot be best response by firm 2 to an action by firm 1 • so it cannot belong to the NE of the subgame • everlasting minimax punishment is not credible in this case April 2018 Frank Cowell: Repeated Games 27

Repeated Cournot game: Payoffs §Space of profits for the two firms §Cournot-Nash outcome §Joint-profit maximisation §Minimax outcomes §Payoffs available in repeated game P 2 P • (PJ, PJ) (PC, PC) 0 April 2018 • P 1 Now review Bertrand competition P Frank Cowell: Repeated Games 28

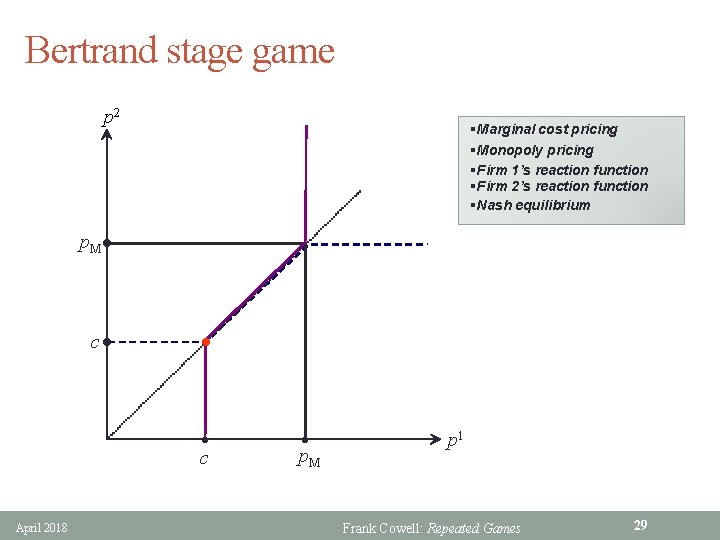
Bertrand stage game p 2 §Marginal cost pricing §Monopoly pricing §Firm 1’s reaction function §Firm 2’s reaction function §Nash equilibrium p. Ml cl l l c April 2018 l p. M p 1 Frank Cowell: Repeated Games 29

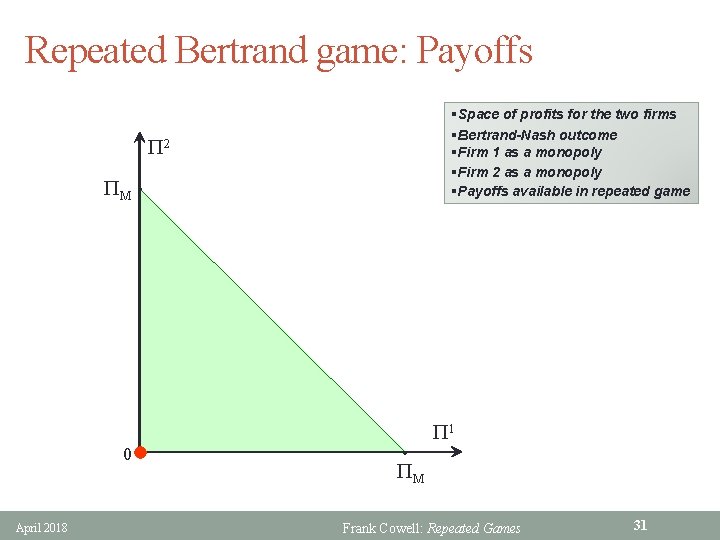
Bertrand competition: repeated § NE of the stage game: • set price equal to marginal cost c • results in zero profits § NE outcome is the minimax outcome • minimax outcome is implementable as a Nash equilibrium • in all the subgames following a defection from cooperation § In repeated Bertrand competition • firms set p. M if acting “cooperatively” • split profits between them • if one firm deviates from this • others then set price to c § Repeated Bertrand: result • can enforce joint profit maximisation through trigger strategy • provided discount factor is large enough April 2018 Frank Cowell: Repeated Games 30

Repeated Bertrand game: Payoffs §Space of profits for the two firms §Bertrand-Nash outcome §Firm 1 as a monopoly §Firm 2 as a monopoly §Payoffs available in repeated game P 2 PM • 0 April 2018 • P 1 PM Frank Cowell: Repeated Games 31

Repeated games: summary § New concepts: • Stage game • History • The Folk Theorem • Trigger strategy § What next? • Games under uncertainty April 2018 Frank Cowell: Repeated Games 32