Game Theory Developed to explain the optimal strategy

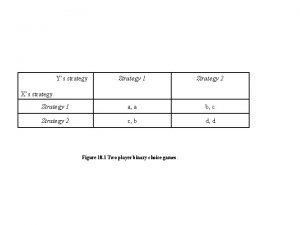
Game Theory • Developed to explain the optimal strategy in two-person interactions. • Initially, von Neumann and Morganstern – Zero-sum games • John Nash – Nonzero-sum games • Harsanyi, Selten – Incomplete information

An example: Big Monkey and Little Monkey Little monkey c w Big monkey w c 0, 0 9, 1 4, 4 5, 3 What should Big Monkey do? • If BM waits, LM will climb – BM gets 9 • If BM climbs, LM will wait – BM gets 4 • BM should wait. • What about LM? • Opposite of BM (even though we’ll never get to the right side of the tree)

An example: Big Monkey and Little Monkey • These strategies (w and cw) are called best responses. – Given what the other guy is doing, this is the best thing to do. • A solution where everyone is playing a best response is called a Nash equilibrium. – No one can unilaterally change and improve things. • This representation of a game is called extensive form.

An example: Big Monkey and Little Monkey • What if the monkeys have to decide simultaneously? Little monkey c w Big monkey w 0, 0 c w c 9, 1 6 -2, 4 7 -2, 3 Now Little Monkey has to choose before he sees Big Monkey move Two Nash equilibria (c, w), (w, c) Also a third Nash equilibrium: Big Monkey chooses between c & w with probability 0. 5 (mixed strategy)

An example: Big Monkey and Little Monkey • It can often be easier to analyze a game through a different representation, called normal form Little Monkey Big Monkey c v c 5, 3 4, 4 v 9, 1 0, 0

Choosing Strategies • In the simultaneous game, it’s harder to see what each monkey should do – Mixed strategy is optimal. • Trick: How can a monkey maximize its payoff, given that it knows the other monkeys will play a Nash strategy? • Oftentimes, other techniques can be used to prune the number of possible actions.

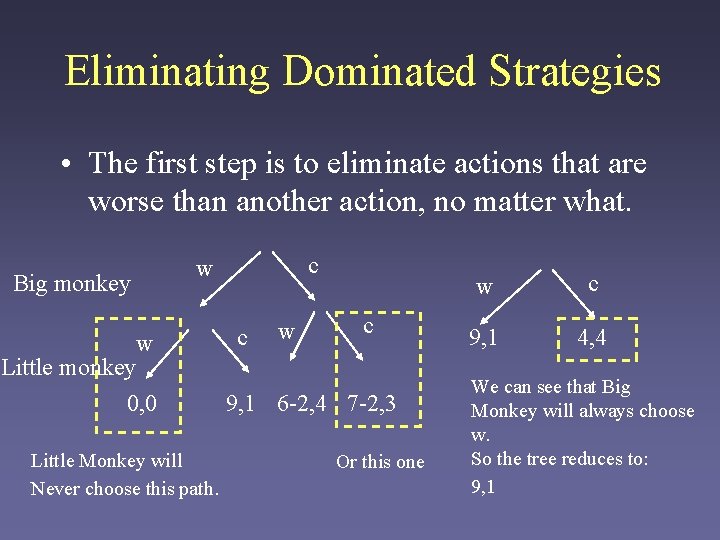
Eliminating Dominated Strategies • The first step is to eliminate actions that are worse than another action, no matter what. Big monkey c w w Little monkey 0, 0 Little Monkey will Never choose this path. c w c 9, 1 6 -2, 4 7 -2, 3 Or this one w c 9, 1 4, 4 We can see that Big Monkey will always choose w. So the tree reduces to: 9, 1

Eliminating Dominated Strategies • We can also use this technique in normalform games: Column a b a 9, 1 4, 4 b 5, 3 0, 0 Row

Eliminating Dominated Strategies • We can also use this technique in normalform games: a b a 9, 1 4, 4 b 5, 3 0, 0 For any column action, row will prefer a.

Eliminating Dominated Strategies • We can also use this technique in normalform games: a b a 9, 1 4, 4 b 5, 3 0, 0 Given that row will pick a, column will pick b. (a, b) is the unique Nash equilibrium.

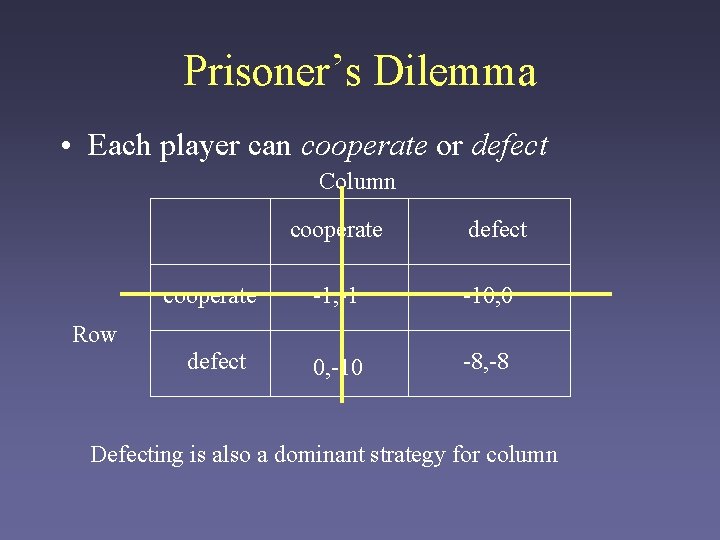
Prisoner’s Dilemma • Each player can cooperate or defect Column cooperate defect cooperate -1, -1 -10, 0 defect 0, -10 -8, -8 Row

Prisoner’s Dilemma • Each player can cooperate or defect Column cooperate defect cooperate -1, -1 -10, 0 defect 0, -10 -8, -8 Row Defecting is a dominant strategy for row

Prisoner’s Dilemma • Each player can cooperate or defect Column cooperate defect cooperate -1, -1 -10, 0 defect 0, -10 -8, -8 Row Defecting is also a dominant strategy for column

Prisoner’s Dilemma • Even though both players would be better off cooperating, mutual defection is the dominant strategy. • What drives this? – One-shot game – Inability to trust your opponent – Perfect rationality

Prisoner’s Dilemma • Relevant to: – – Arms negotiations Online Payment Product descriptions Workplace relations • How do players escape this dilemma? – Play repeatedly – Find a way to ‘guarantee’ cooperation – Change payment structure

Definition of Nash Equilibrium • A game has n players. • Each player i has a strategy set Si – This is his possible actions • Each player has a payoff function – p. I: S R • A strategy ti in Si is a best response if there is no other strategy in Si that produces a higher payoff, given the opponent’s strategies.

Definition of Nash Equilibrium • A strategy profile is a list (s 1, s 2, …, sn) of the strategies each player is using. • If each strategy is a best response given the other strategies in the profile, the profile is a Nash equilibrium. • Why is this important? – If we assume players are rational, they will play Nash strategies. – Even less-than-rational play will often converge to Nash in repeated settings.

An Example of a Nash Equilibrium Column a b a 1, 2 0, 1 b 2, 1 1, 0 Row (b, a) is a Nash equilibrium. To prove this: Given that column is playing a, row’s best response is b. Given that row is playing b, column’s best response is a.

Finding Nash Equilibria – Dominated Strategies • What to do when it’s not obvious what the equilibrium is? • In some cases, we can eliminate dominated strategies. – These are strategies that are inferior for every opponent action. • In the previous example, row = a is dominated.

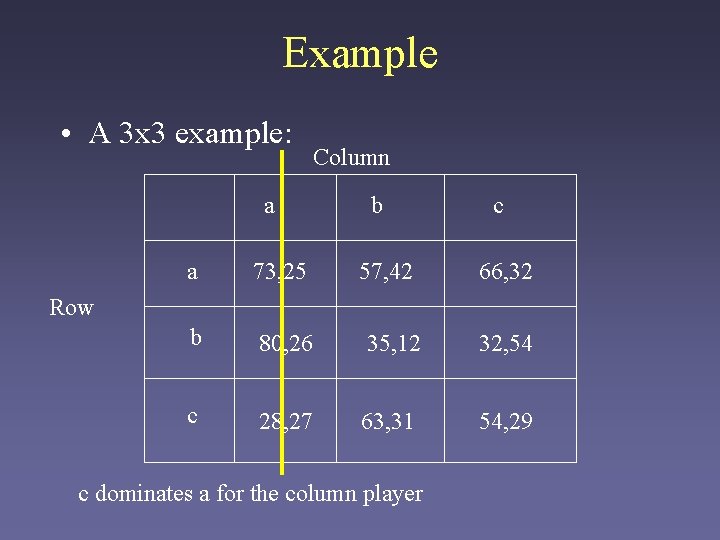
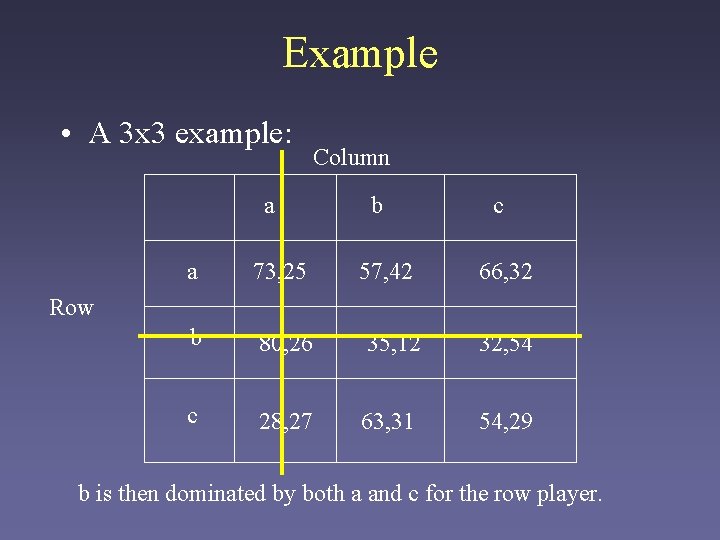
Example • A 3 x 3 example: Column a b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row

Example • A 3 x 3 example: a Column b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row c dominates a for the column player

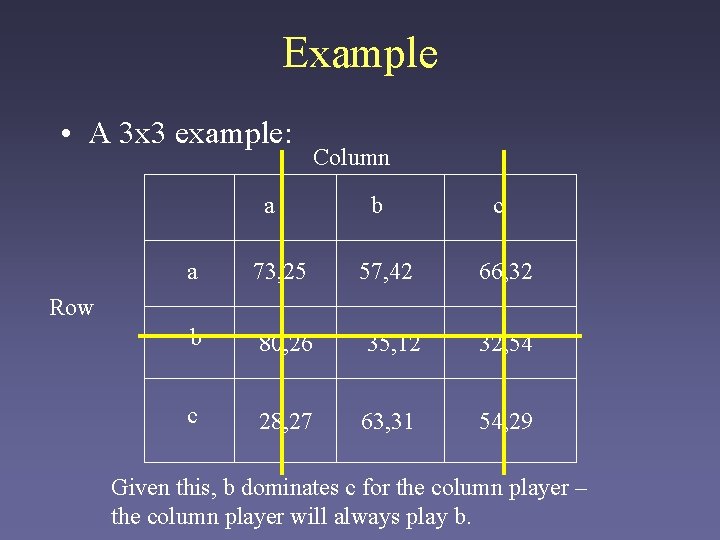
Example • A 3 x 3 example: a Column b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row b is then dominated by both a and c for the row player.

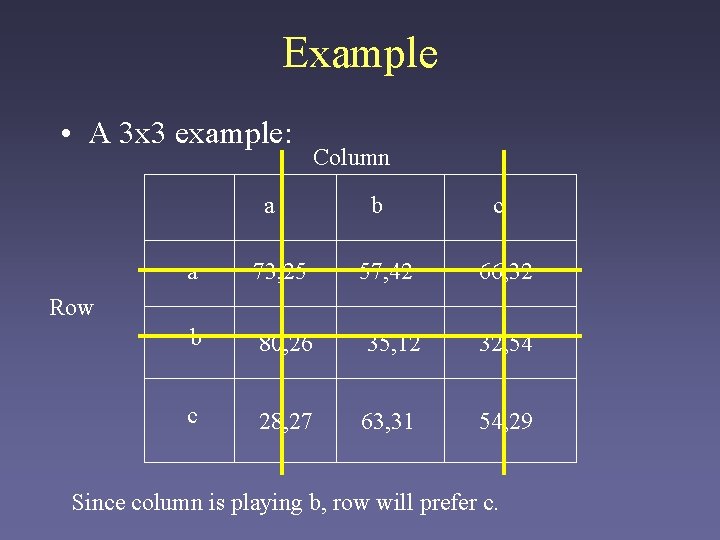
Example • A 3 x 3 example: a Column b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row Given this, b dominates c for the column player – the column player will always play b.

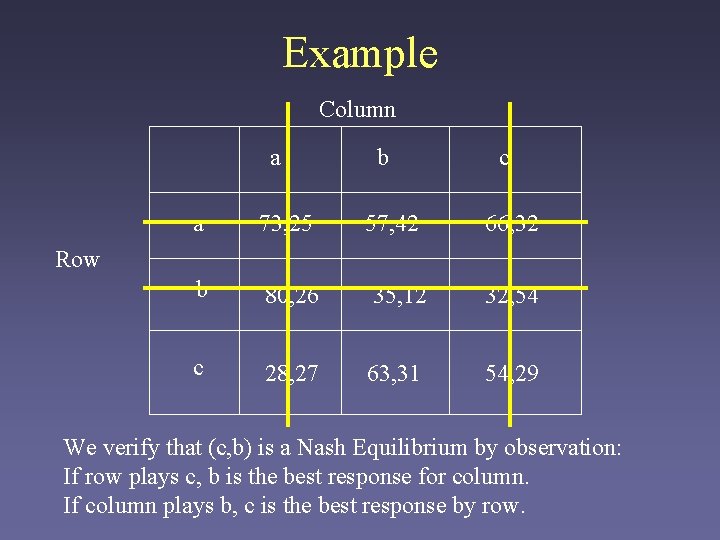
Example • A 3 x 3 example: a Column b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row Since column is playing b, row will prefer c.

Example Column a b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Row We verify that (c, b) is a Nash Equilibrium by observation: If row plays c, b is the best response for column. If column plays b, c is the best response by row.

Example #2 • You try this one: Column a b c a 2, 2 1, 1 4, 0 b 1, 2 4, 1 3, 5 Row

Coordination Games • Consider the following problem: – A supplier and a buyer need to decide whether to adopt a new purchasing system. Buyer new old new 20, 20 0, 0 old 0, 0 5, 5 Supplier No dominated strategies!

Coordination Games Supplier Buyer new old new 20, 20 0, 0 old 0, 0 5, 5 • This game has two Nash equilibria (new, new) and (old, old) • Real-life examples: Beta vs VHS, Mac vs Windows vs Linux, others? • Each player wants to do what the other does • which may be different than what they say they’ll do • How to choose a strategy? Nothing is dominated.

Solving Coordination Games • Coordination games turn out to be an important real-life problem – Technology/policy/strategy adoption, delegation of authority, synchronization • Human agents tend to use “focal points” – Solutions that seem to make “natural sense” • e. g. pick a number between 1 and 10 • Social norms/rules are also used – Driving on the right/left side of the road • These strategies change the structure of the game

Price-matching Example • Two sellers are offering the same book for sale. • This book costs each seller $25. • The lowest price gets all the customers; if they match, profits are split. • What is the Nash Equilibrium strategy?

Mixed strategies • Unfortunately, not every game has a pure strategy equilibrium. – Rock-paper-scissors • However, every game has a mixed strategy Nash equilibrium. • Each action is assigned a probability of play. • Player is indifferent between actions, given these probabilities.

Mixed Strategies • In many games (such as coordination games) a player might not have a pure strategy. • Instead, optimizing payoff might require a randomized strategy (also called a mixed strategy) Wife football shopping football 2, 1 0, 0 shopping 0, 0 1, 2 Husband

Strategy Selection Wife football Husband shopping football 2, 1 0, 0 shopping 0, 0 1, 2 If we limit to pure strategies: Husband: U(football) = 0. 5 * 2 + 0. 5 * 0 = 1 U(shopping) = 0. 5 * 0 + 0. 5 * 1 = ½ Wife: U(shopping) = 1, U(football) = ½ Problem: this won’t lead to coordination!

Mixed strategy • Instead, each player selects a probability associated with each action – Goal: utility of each action is equal – Players are indifferent to choices at this probability • a=probability husband chooses football • b=probability wife chooses shopping • Since payoffs must be equal, for husband: – b*1=(1 -b)*2 b=2/3 • For wife: – a*1=(1 -a)*2 = 2/3 • In each case, expected payoff is 2/3 – 2/9 of time go to football, 2/9 shopping, 5/9 miscoordinate • If they could synchronize ahead of time they could do better.

Example: Rock paper scissors Column rock paper scissors rock 0, 0 -1, 1 1, -1 paper 1, -1 0, 0 -1, 1 scissors -1, 1 1, -1 0, 0 Row

Setup • Player 1 plays rock with probability pr, scissors with probability ps, paper with probability 1 -pr –ps • P 2: Utility(rock) = 0*pr + 1*ps – 1(1 -pr –ps) = 2 ps + pr -1 • P 2: Utility(scissors) = 0*ps + 1*(1 – pr – ps) – 1 pr = 1 – 2 pr –ps • P 2: Utility(paper) = 0*(1 -pr –ps)+ 1*pr – 1 ps = pr –ps Player 2 wants to choose a probability for each strategy so that the expected payoff for each strategy is the same.

Repeated games • Many games get played repeatedly • A common strategy for the husband-wife problem is to alternate – This leads to a payoff of 1, 2, … – 1. 5 per week. • Requires initial synchronization, plus trust that partner will go along. • Difference in formulation: we are now thinking of the game as a repeated set of interactions, rather than as a one-shot exchange.

Repeated vs Stage Games • There are two types of multiple-action games: – Stage games: players take a number of actions and then receive a payoff. • Checkers, chess, bidding in an ascending auction – Repeated games: Players repeatedly play a shorter game, receiving payoffs along the way. • Poker, blackjack, rock-paper-scissors, etc

Analyzing Stage Games • Analyzing stage games requires backward induction • We start at the last action, determine what should happen there, and work backwards. – Just like a game tree with extensive form. • Strange things can happen here: – Centipede game • Players alternate – can either cooperate and get $1 from nature or defect and steal $2 from your opponent • Game ends when one player has $100 or one player defects.

Analyzing Repeated Games • Analyzing repeated games requires us to examine the expected utility of different actions. • Assumption: game is played “infinitely often” – Weird endgame effects go away. • Prisoner’s Dilemma again: – In this case, tit-for-tat outperforms defection. • Collusion can also be explained this way. – Short-term cost of undercutting is less than long-run gains from avoiding competition.