Chapter 12 Game Theory Introduction Game theory provides

Chapter 12 Game Theory

Introduction § Game theory provides tools to model strategic interaction among economic agents. § Strategic interaction refers to situations where outcomes depend on the choices of all agents. § Game theory was pioneered by John von Neumann and Oskar Morgenstern in their 1944 book, Theory of Games and Economic Behavior § John Nash developed the fundamental notion of equilibrium in simultaneous-move games, the Nash equilibrium, in the early 1950 s 2

Introduction § In the 1960 s, John Harsanyi extended game theory to include uncertainty, developing the idea of a Bayesian Nash equilibrium § Reinhardt Selten expanded the range of game theory by considering sequential games with its corresponding notion of subgame perfect Nash equilibrium. § All three were awarded the 1994 Nobel Prize in Economics. 3

12. 1 Static Games A game consists of three basic elements: § the players, § their strategies, and § the payoffs § In a static game, all players decide on their stategies simultaniously without being able to see what others are doing. 4

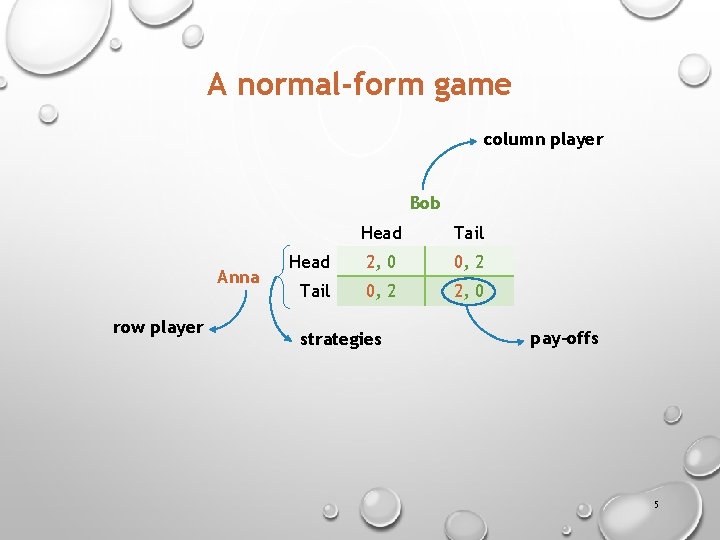
A normal-form game column player Bob Anna row player Head Tail Head 2, 0 0, 2 Tail 0, 2 2, 0 strategies pay-offs 5

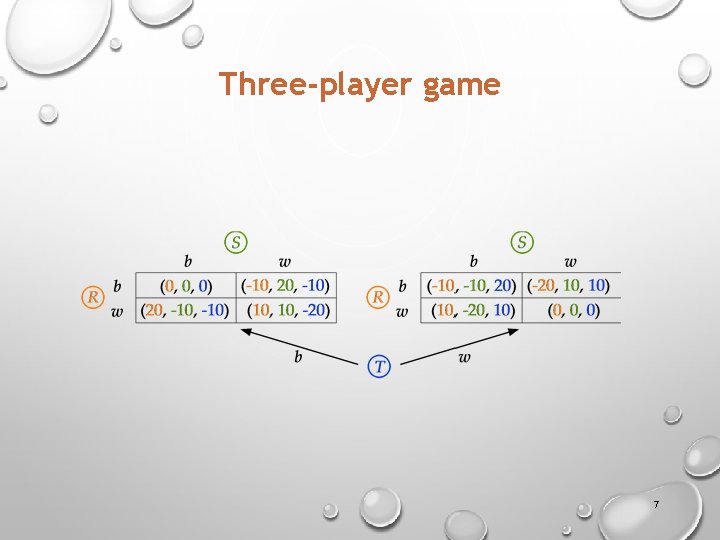
Three-player game Three players: neighboring hotels on an interstate highway: § Relax Inn (R), § Sleep Motel (S), and § Take-Five Lodge (T). Strategies: § Offer basic broadband internet access (b), or § high-speed Wi-Fi internet access (w) 6

Three-player game 7

12. 2 Solving Static Games We introduce two basic solution concepts for solving games: § dominant strategy equilibrium § Nash equilibrium 8

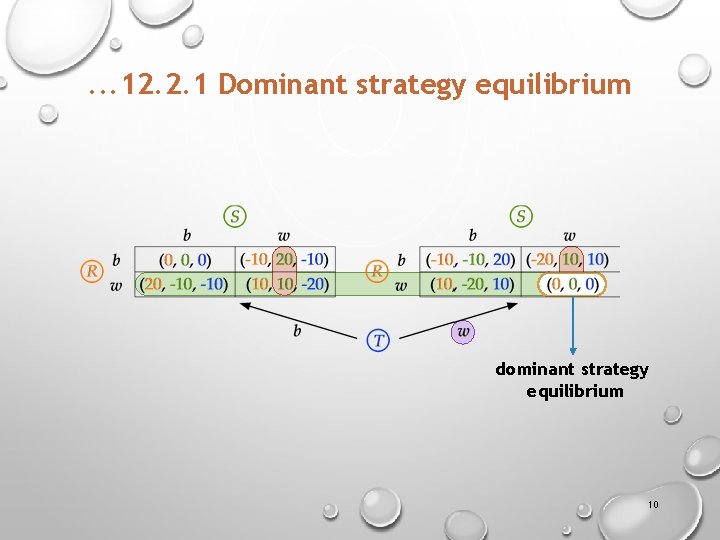
12. 2. 1 Dominant strategy equilibrium A player has a dominant strategy if there is one strategy that is the best in terms of this player’s payoffs, regardless of what others are doing. dominant strategy for Mahala Aruna Mahala $10 $15 $10 50, 50 80, 30 $15 30, 80 45, 45 dominant strategy for Aruna 9

. . . 12. 2. 1 Dominant strategy equilibrium dominant strategy equilibrium 10

Prisoners’ Dilemma Prisoner 2 Talk Prisoner 1 Talk -10, -10 Be silent -20, 0 Be silent 0, -20 -1, -1 dominant strategy equilibrium § The Prisoners’ Dilemma is a dilemma because when the prisoners follow their own self-interest and play their dominant strategies, they end up in prison for 10 years each at the DSE, when instead they both would have been better off being in prison for one year if the two could find a way to remain silent. 11

12. 2. 2 Nash equilibrium § At Nash Equilibrium, unilateral deviation does not pay, i. e. no player gains by changing her stategy on her own. § There are two ways to find a NE Ø method of unilateral deviation Ø method of mutual best-response 12

Method of unilateral deviation Babur Akbar Call Wait Call 0, 0 1, 2 Wait 2, 1 0, 0 § To use the method of unilateral deviation, list all the possible candidates for a NE: § (i) (Call, Call); § (ii) (Call, Wait); § (iii) (Wait, Call); and, § (iv) (Wait, Wait). 13

. . . Method of unilateral deviation § At (i), Akbar receives a utility of zero. If he deviates to wait while Babur is calling, then his utility jumps to 2, so a unilateral deviation by Akbar pays off. Ergo this cannot be a NE. § At (ii) if Akbar deviates while Babur is waiting, his utility decreases to zero, so unilateral deviation does not pay for Akbar. § For this to be a NE, Babur must also not want to deviate unilaterally. At (ii), Babur, while waiting, receives a utility of 2, so if he deviates to calling when Akbar is calling, his utility drops to zero. Thus neither player gains from deviation and so this is a NE. 14

. . . Method of unilateral deviation § In a similar manner, it can be checked that (Wait, Call) is also a NE, 4 while (Wait, Wait) is not. § Hence, there are two Nash equilibria in this game. § The solution is not exactly predictive § In the real world, there may be some social norms or customs that determine which of the two NE will actually come about 15

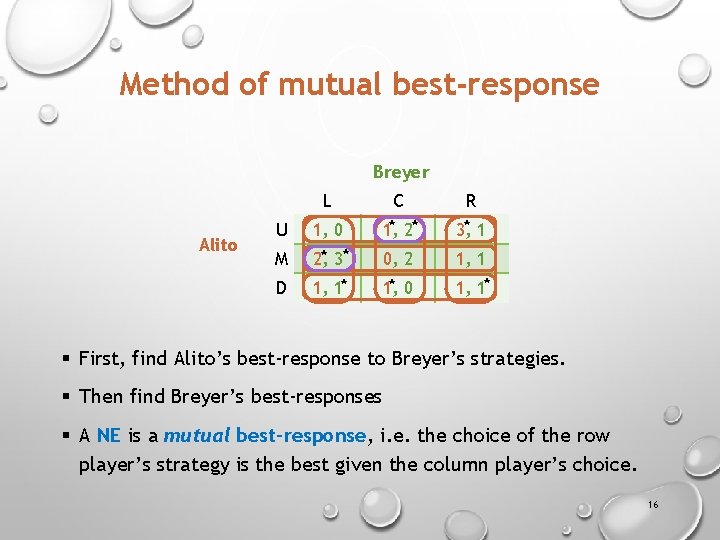
Method of mutual best-response Breyer L Alito U M D 1, 0 2, * 3* 1, 1* C * 2* 1, R 3, * 1 0, 2 * 0 1, 1* § First, find Alito’s best-response to Breyer’s strategies. § Then find Breyer’s best-responses § A NE is a mutual best-response, i. e. the choice of the row player’s strategy is the best given the column player’s choice. 16

Relationship between a NE and a DSE § A NE is a configuration of strategies where no single player wants to change their strategy given what the other players are doing. § At a DSE, no player wants to deviate regardless of what the others are doing. § Every DSE must be a NE. 17

12. 2. 3 Mixed strategies § pure strategies: each player chooses a strategy for sure, either H or T, with probability 1 § mixed strategies § Nash’s brilliant discovery was that all games (with finitely many players who have finitely many strategies) always have at least one NE when you allow for mixed strategies. 18

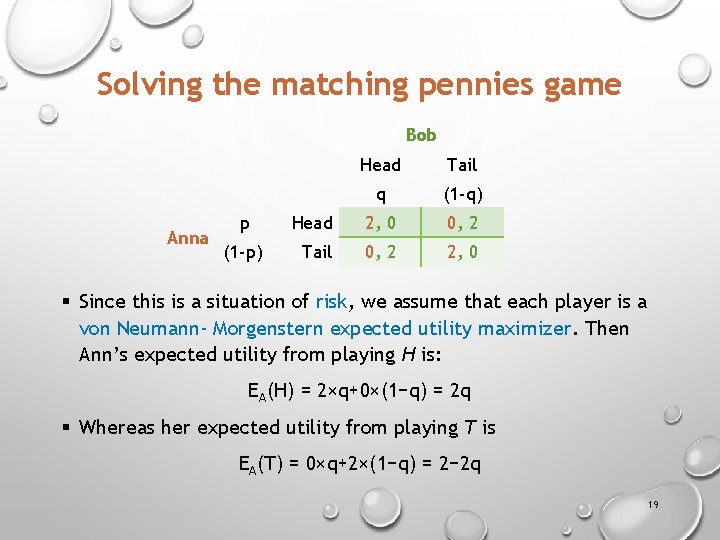
Solving the matching pennies game Bob Anna Head Tail q (1 -q) p Head 2, 0 0, 2 (1 -p) Tail 0, 2 2, 0 § Since this is a situation of risk, we assume that each player is a von Neumann- Morgenstern expected utility maximizer. Then Ann’s expected utility from playing H is: EA(H) = 2×q+0×(1−q) = 2 q § Whereas her expected utility from playing T is EA(T) = 0×q+2×(1−q) = 2− 2 q 19

. . . Solving the matching pennies game § Similarly, Bob’s expected utility from playing H is EB(H) = 0 × p + 2 × (1 − p) = 2 − 2 p, § While his expected utility from playing T is EB(T) = 2 × p + 0 × (1 − p) = 2 p. § A Nash Equilibrium in mixed stategies is one where no one wants to change their own mixed stategy, given the mixed stategy of the other players. § In this instance, it means that Ann’s choice of p has to be a best -response to Bob’s choice of q, and vice versa. 20

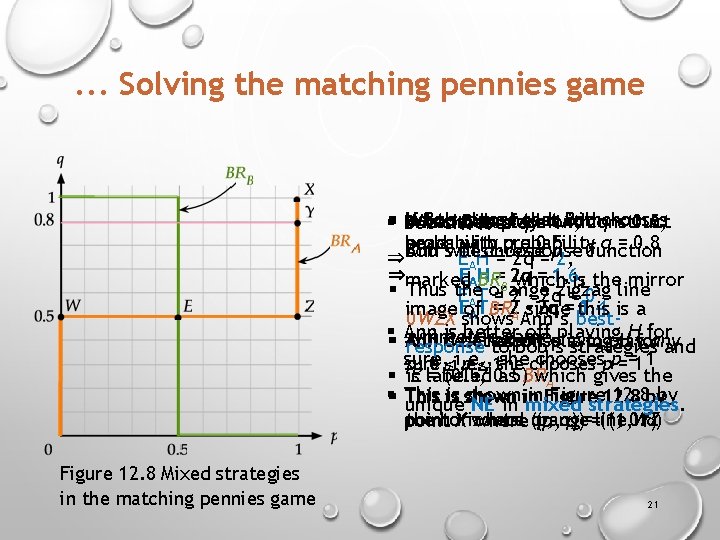
. . . Solving the matching pennies game § Bob Next suppose Bob If Bob plays heads with When Bob plays with qchooses < 0. 5, In a chooses similar fashion, construct qthat =1 heads with probability q = 0. 8 probability q = 0. 5 Ann will choose p = 0 Bob’s best-response function ⇒ EAH = 2 q = 2, ⇒marked EAH =B 2 q = 1. 6, 1, is the mirror BR which § Thus the orange EAT = 2 - 2 qzigzag = 0 line Eof = 2 A -since 2 q = this 0. 4 1 is a image AT BR 0 WZX shows Ann’s best§§ Ann is better offplaying Hfor symmetric game. Ann is better off H best-response is to play response to Bob’s strategiesany and sure, i. e. , she chooses p = 1 sure, p, 0 ≤i. e. , p ≤ 1 she chooses p = 1 as BR § is. E labeled = (0. 5, 0. 5) which gives the A § This shown in. Figure 12. 8 byby 12. 8 This is shown unique NE in in mixed strategies. YX where (1, the horizontal orange WZ point where (p, q) q)==line (1, 0. 8) 1) Figure 12. 8 Mixed strategies in the matching pennies game 21

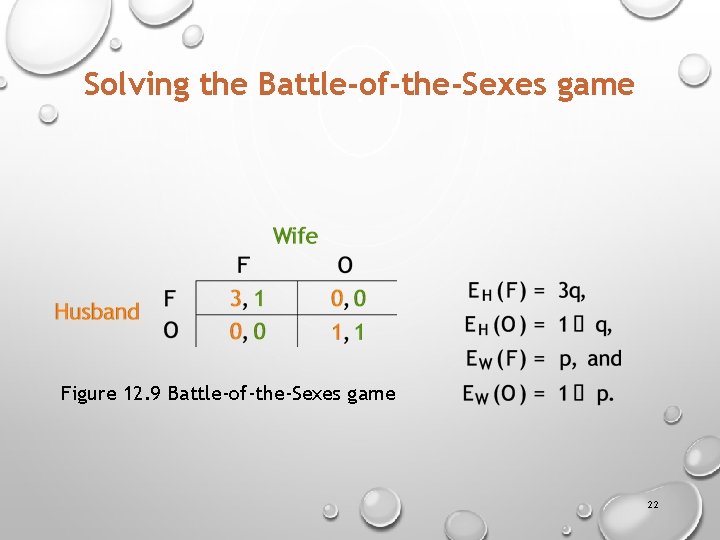
Solving the Battle-of-the-Sexes game Figure 12. 9 Battle-of-the-Sexes game 22

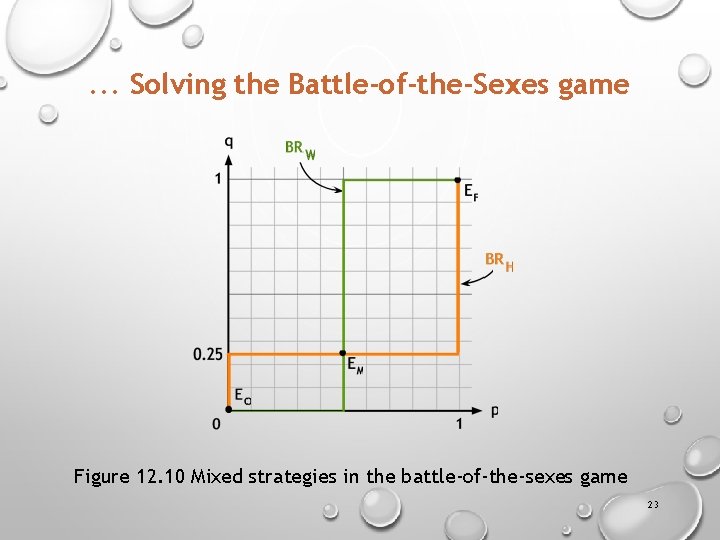
. . . Solving the Battle-of-the-Sexes game Figure 12. 10 Mixed strategies in the battle-of-the-sexes game 23

12. 3 Dynamic Games § Dynamic games en- large the scope of game theory by allowing players to move sequentially § Two features of Dynamic games: Ø the timing of the play (who moves at what point) Ø what information the players have 24

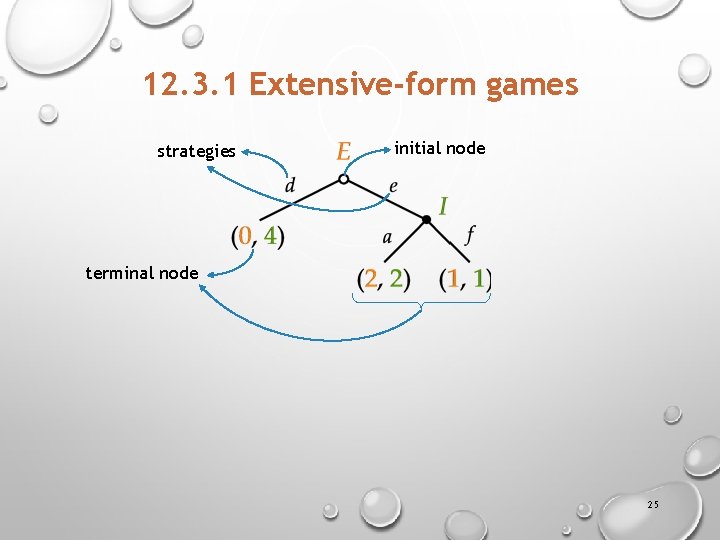
12. 3. 1 Extensive-form games strategies initial node terminal node 25

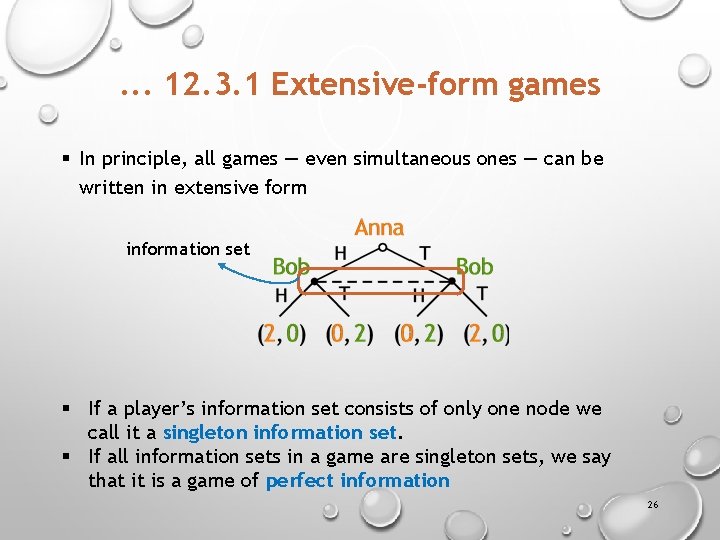
. . . 12. 3. 1 Extensive-form games § In principle, all games — even simultaneous ones — can be written in extensive form information set § If a player’s information set consists of only one node we call it a singleton information set. § If all information sets in a game are singleton sets, we say that it is a game of perfect information 26

12. 3. 2 Subgame perfect Nash equilibrium § In this chapter, we will restrict attention to games of perfect information all of which can be solved by backward induction. § We assume the common knowledge of rationality on the part of all players § All players know that at any decision node, if the player at that node has a choice that leads to a strictly higher pay-off compared to any other strategy, then she will choose the former. § A subgame is a subset of the extensive-form game that contains a singleton initial node and all the nodes below that can be reached from it. 27

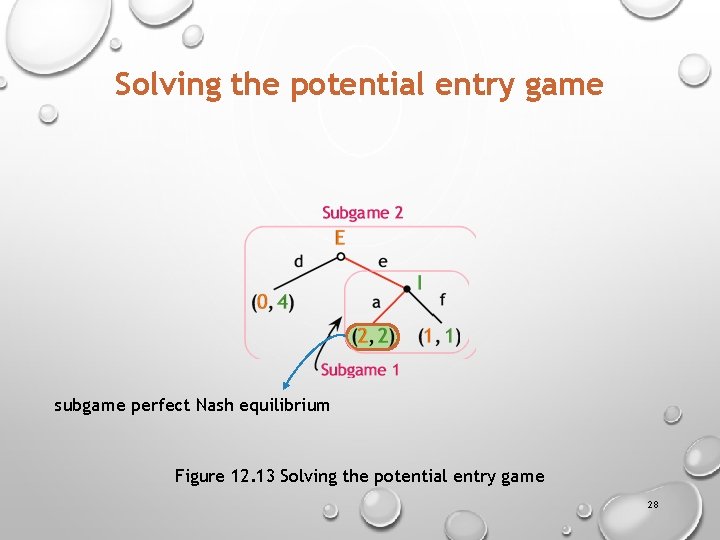
Solving the potential entry game subgame perfect Nash equilibrium Figure 12. 13 Solving the potential entry game 28

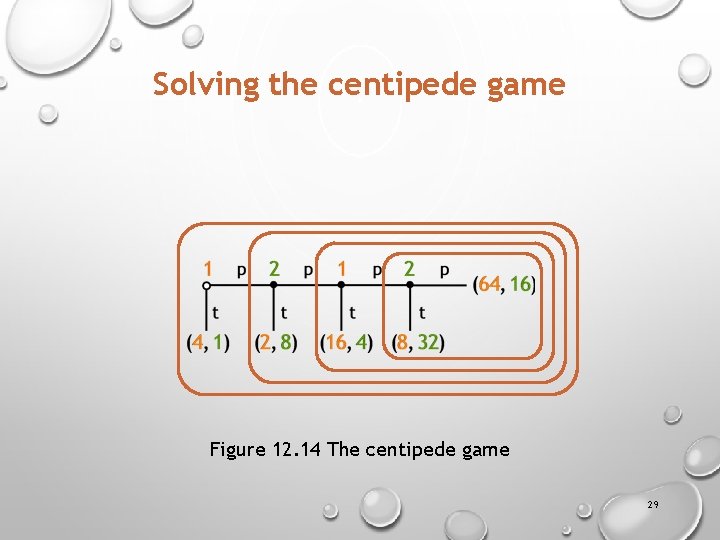
Solving the centipede game Figure 12. 14 The centipede game 29