Game Theory Teori Permainan Game Theory Pendekatan matematis

Game Theory ( Teori Permainan )

Game Theory Pendekatan matematis yang digunakan untuk merumuskan situasi pertentangan (konflik) antar berbagai kepentingan dipelopori : John Vonn Neumann (ahli Matematika) dan Oskar Morgestern (ahli ekonomi) pada tahun 1944

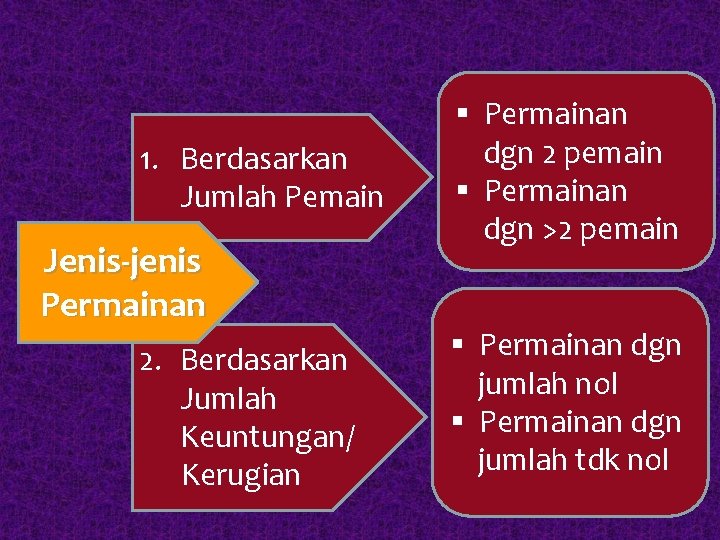
1. Berdasarkan Jumlah Pemain Jenis-jenis Permainan 2. Berdasarkan Jumlah Keuntungan/ Kerugian § Permainan dgn 2 pemain § Permainan dgn >2 pemain § Permainan dgn jumlah nol § Permainan dgn jumlah tdk nol

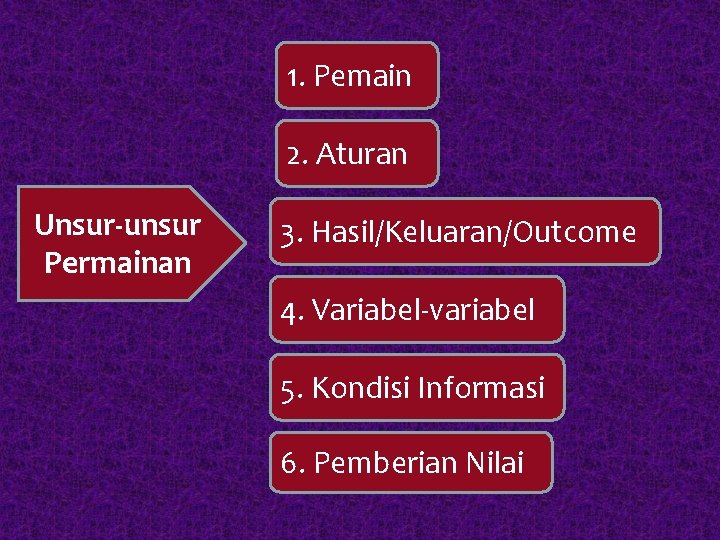
1. Pemain 2. Aturan Unsur-unsur Permainan 3. Hasil/Keluaran/Outcome 4. Variabel-variabel 5. Kondisi Informasi 6. Pemberian Nilai

Permainan Dua Pemain dengan jumlah nol (Zero Sum Game) model pertentangan yang paling umum dalam dunia bisnis dimainkan oleh dua orang pemain atau dua organisasi yang secara langsung mempunyai kepentingan yang berhadapan.

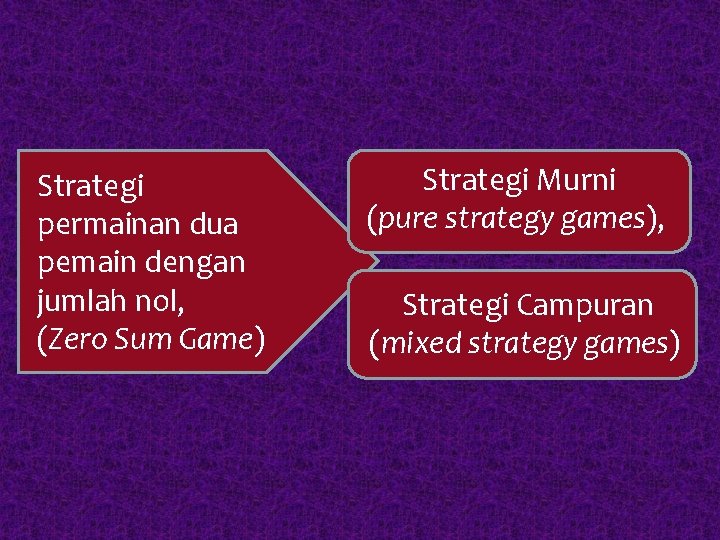
Strategi permainan dua pemain dengan jumlah nol, (Zero Sum Game) Strategi Murni (pure strategy games), Strategi Campuran (mixed strategy games)

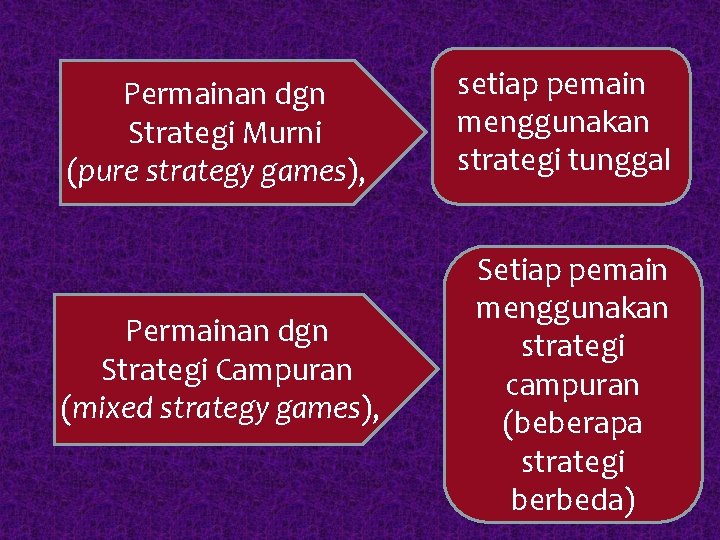
Permainan dgn Strategi Murni (pure strategy games), setiap pemain menggunakan strategi tunggal Permainan dgn Strategi Campuran (mixed strategy games), Setiap pemain menggunakan strategi campuran (beberapa strategi berbeda)

Permainan dengan Strategi Murni (pure strategy games) § Permainan digambarkan dalam sebuah tabel (matriks pay off). § Pemain pertama menempati baris dan pemain kedua menempati kolom atau sebaliknya. § Penyelesaian dilakukan dengan menggunakan konsep maksimin untuk pemain baris dan minimaks untuk pemain kolom. § Pemain akan menggunakan strategi tunggal utk mendapat hasil optimal. saddle point yang sama

Dalam permainan strategi murni : § strategi optimal pemain baris menggunakan kriteria maksimin (maksimal diantara yg minimal) § strategi optimal pemain kolom menggunakan kriteria minimaks (minimal diantara yg maksimal) Nilai yang dicapai harus merupakan : § maksimum dari minimaks baris, dan § minimum dari maksimin kolom.

Jika nilai maksimin = nilai minimaks telah tercapai titik keseimbangan (equilibrium/titik pelana/saddle point).

Jika nilai maksimin nilai minimaks Tidak tercapai titik keseimbangan permainan tidak dapat diselesaikan dengan strategi murni,

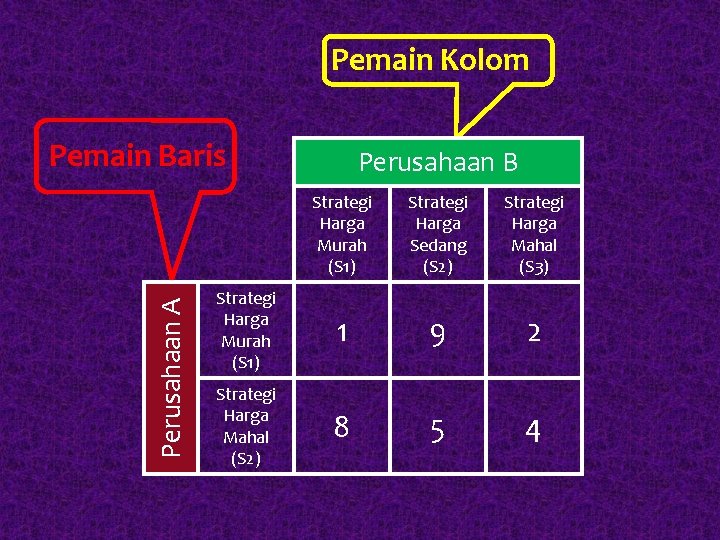
Contoh 1 : Dua perusahaan A dan B bersaing untuk mendapatkan keuntungan dari pangsa pasar yang ada dengan mengandalkan strategi masing-masing. Perusahaan A mengandalkan 2 (dua) strategi dan perusahaan B memiliki 3 (tiga) strategi. Nilai capaian keuntungan dari strategi masing perusahan digambarkan dalam tabel berikut :

Pemain Kolom Perusahaan A Pemain Baris Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 1 9 2 Strategi Harga Mahal (S 2) 8 5 4

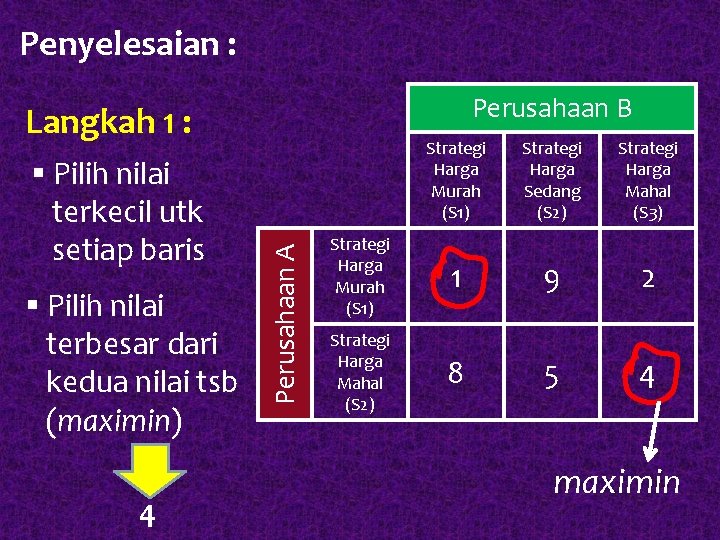
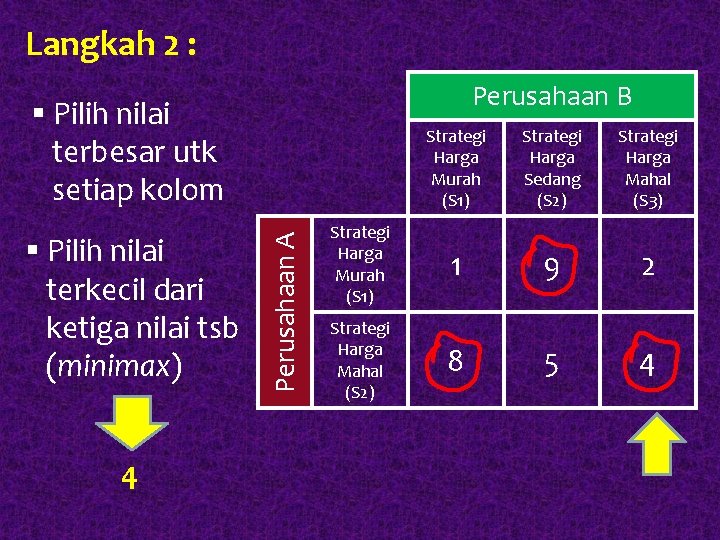
Penyelesaian : Perusahaan B § Pilih nilai terkecil utk setiap baris § Pilih nilai terbesar dari kedua nilai tsb (maximin) 4 Perusahaan A Langkah 1 : Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 1 9 2 Strategi Harga Mahal (S 2) 8 5 4 maximin

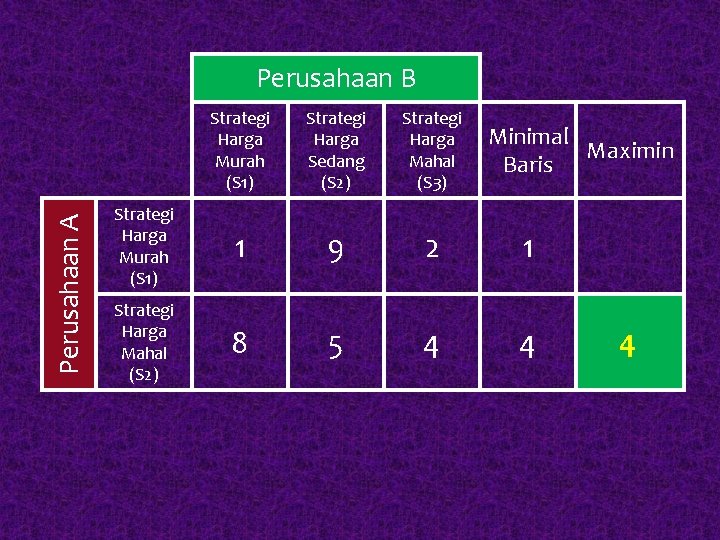
Perusahaan A Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 1 9 2 1 Strategi Harga Mahal (S 2) 8 5 4 4 Minimal Maximin Baris 4

Langkah 2 : Perusahaan B § Pilih nilai terkecil dari ketiga nilai tsb (minimax) 4 Perusahaan A § Pilih nilai terbesar utk setiap kolom Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 1 9 2 Strategi Harga Mahal (S 2) 8 5 4

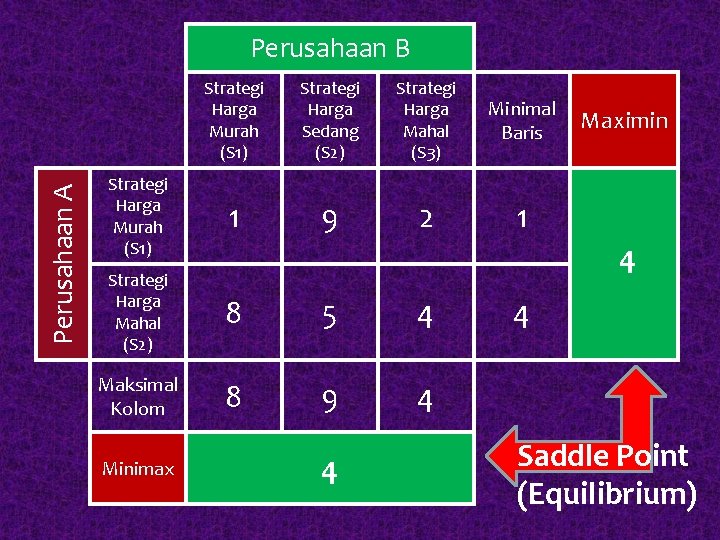
Perusahaan A Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Minimal Baris Strategi Harga Murah (S 1) 1 9 2 1 Strategi Harga Mahal (S 2) 8 5 4 Maksimal Kolom 8 9 4 Minimax Maximin 4 4 4 Saddle Point (Equilibrium)

Langkah 3 : Kesimpulan : Apa kira-kira makna dari hasil yang diperoleh ? “Dengan strategi murni terjadi equilibrium dengan nilai 4 “

Langkah 3 : Kesimpulan : § Pemain baris dan pemain kolom memiliki pilihan strategi optimal dengan nilai sama = 4 § Hal ini menunjukkan bahwa : • perusahaan A dengan strategi harga mahal (S 3) akan memperoleh keuntungan aksimal 4. • perusahaan B yg merespon perusahaan A dgn strategi harga mahal (S 3) akan mengalami kerugian minimal 4.

Permainan dengan Strategi Campuran (mixed strategy games)

Permainan dengan Strategi Campuran (mixed strategy games) Strategi ini dilakukan bila strategi murni belum memberi penyelesaian optimal. Sehingga perlu dilakukan tindak lanjut untuk mendapatkan titik optimal saddle point yang sama (equilibrium)

Contoh 2: Dari kasus pada contoh 1, karena terjadi perkembangan di pasar, perusahaan A mengeluarkan strategi baru dengan mengeluarkan juga produk berharga sedang. Nilai capaian keuntungan dari strategi masing perusahan digambarkan dalam tabel berikut :

Perusahaan A Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) 2 5 7 Strategi Harga Sedang (S 2) 1 2 4 Strategi Harga Mahal (S 3) 6 1 9 Strategi Baru

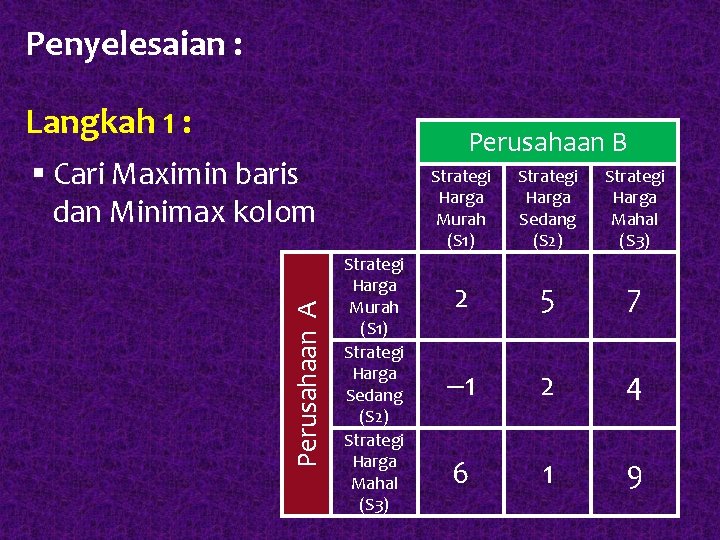
Penyelesaian : Langkah 1 : Perusahaan B Perusahaan A § Cari Maximin baris dan Minimax kolom Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) 2 5 7 1 2 4 6 1 9

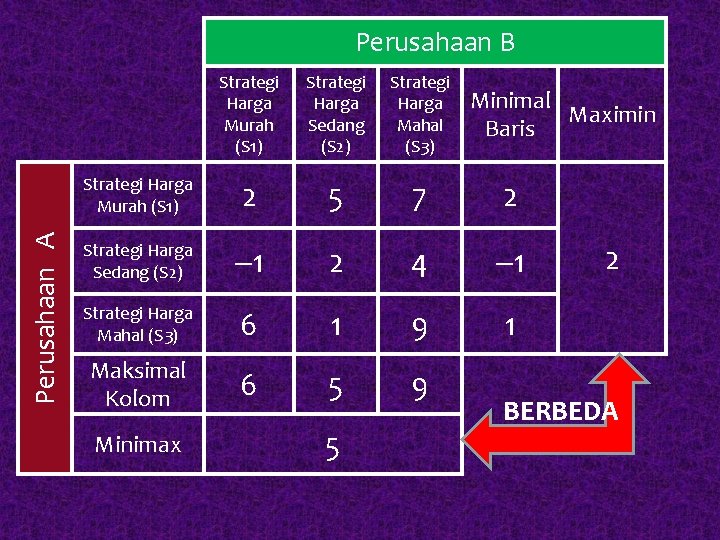
Perusahaan A Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 2 5 7 2 Strategi Harga Sedang (S 2) 1 2 4 1 Strategi Harga Mahal (S 3) 6 1 9 1 Maksimal Kolom 6 5 9 Minimax 5 Minimal Maximin Baris 2 BERBEDA

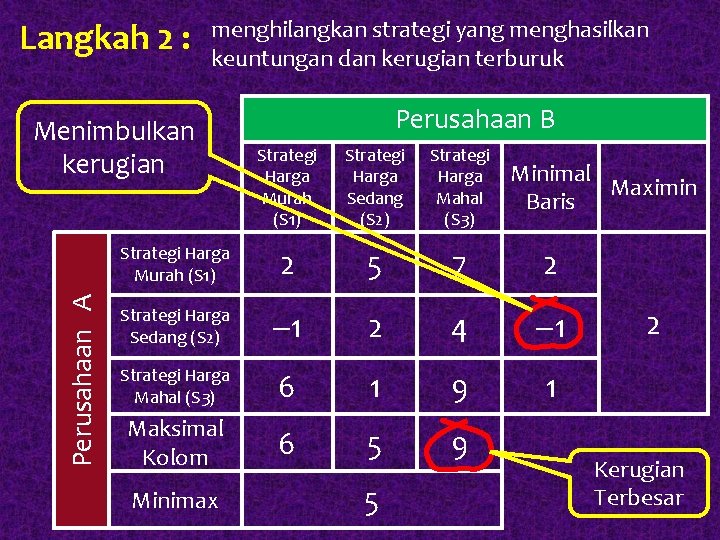
Langkah 2 : menghilangkan strategi yang menghasilkan keuntungan dan kerugian terburuk Perusahaan A Menimbulkan kerugian Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Mahal (S 3) Strategi Harga Murah (S 1) 2 5 7 2 Strategi Harga Sedang (S 2) 1 2 4 1 Strategi Harga Mahal (S 3) 6 1 9 1 Maksimal Kolom 6 5 9 Minimax 5 Minimal Maximin Baris 2 Kerugian Terbesar

§ Bagi perusahaan A : strategi S 2 adalah strategi terburuk, karena dapat menimbulkan kerugian (ada nilai minus) strategi S 2 perusahaan A dihilangkan § Bagi perusahaan B : Strategi S 3 adalah paling buruk karena bisa menimbulkan kerugian terbesar strategi S 3 perusahaan B dihilangkan

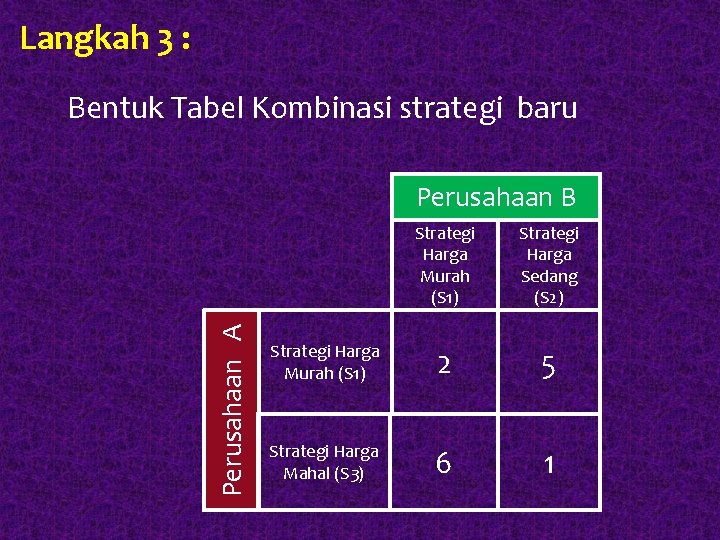
Langkah 3 : Bentuk Tabel Kombinasi strategi baru Perusahaan A Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) Strategi Harga Murah (S 1) 2 5 Strategi Harga Mahal (S 3) 6 1

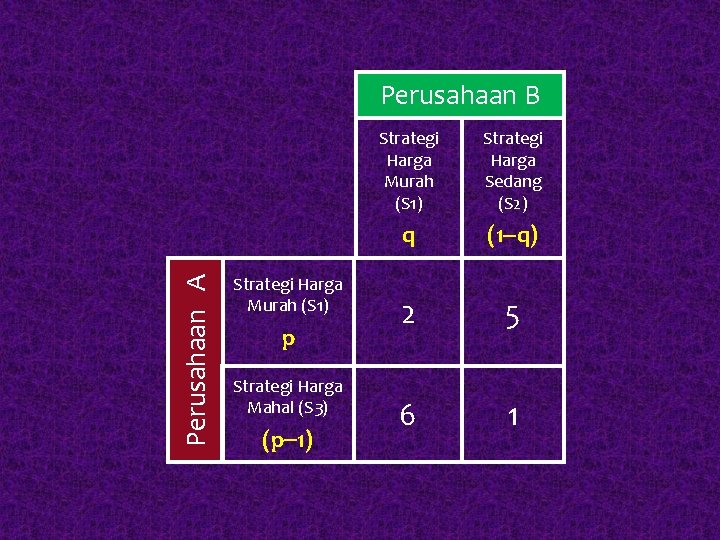
Langkah 4 : Memberikan nilai probabilitas terhadap kemungkinan digunakannya kedua strategi oleh masing-masing perusahaan. § Untuk Perusahaan A : Misal probabilitas keberhasilan penggunaan strategi S 1 = p, maka probabilitas keberhasilan penggunaan strategi S 3 = 1 p § Untuk Perusahaan B : Misal probabilitas keberhasilan penggunaan strategi S 1 = q, maka probabilitas keberhasilan penggunaan strategi S 3 = 1 q

Perusahaan A Perusahaan B Strategi Harga Murah (S 1) p Strategi Harga Mahal (S 3) (p 1) Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) q (1 q) 2 5 6 1

Langkah 5 : Mencari besaran probabilitas setiap strategi untuk menghitung saddle point yg optimal

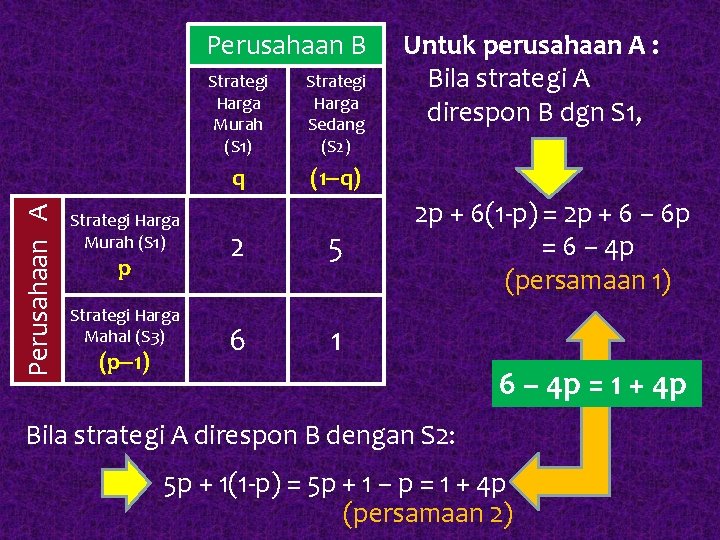
Perusahaan A Perusahaan B Strategi Harga Murah (S 1) p Strategi Harga Mahal (S 3) (p 1) Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) q (1 q) 2 5 6 1 Untuk perusahaan A : Bila strategi A direspon B dgn S 1, 2 p + 6(1 -p) = 2 p + 6 – 6 p = 6 – 4 p (persamaan 1) 6 – 4 p = 1 + 4 p Bila strategi A direspon B dengan S 2: 5 p + 1(1 -p) = 5 p + 1 – p = 1 + 4 p (persamaan 2)

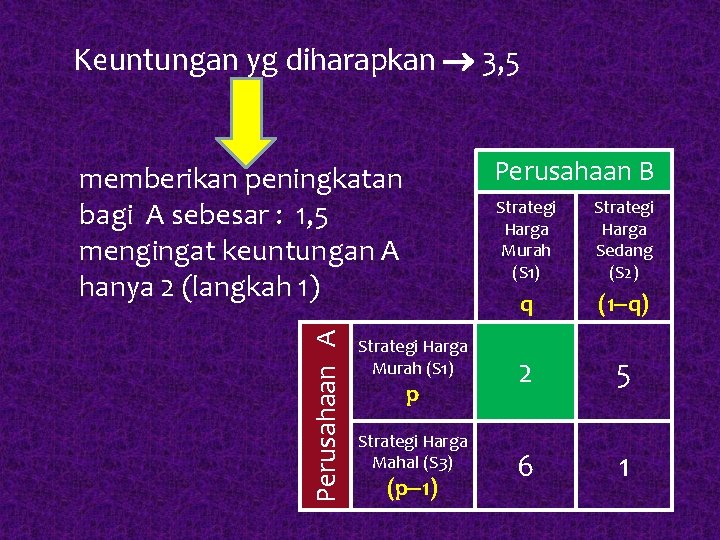
6 – 4 p = 1 + 4 p 8 p = 5 P = 5/8 = 0, 625 Jika p = 0, 625 1 – p = 0, 375 Masukkan nilai p dan (1 -p) pada pers. 1 & 2 (1) : 2 p + 6(1 -p) = 2(0, 625) + 6(0, 375) = 3, 5 (2) : 5 p + 1(1 -p) = 5(0, 625) + 1(0, 375) = 3, 5

Keuntungan yg diharapkan 3, 5 Perusahaan B Perusahaan A memberikan peningkatan bagi A sebesar : 1, 5 mengingat keuntungan A hanya 2 (langkah 1) Strategi Harga Murah (S 1) p Strategi Harga Mahal (S 3) (p 1) Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) q (1 q) 2 5 6 1

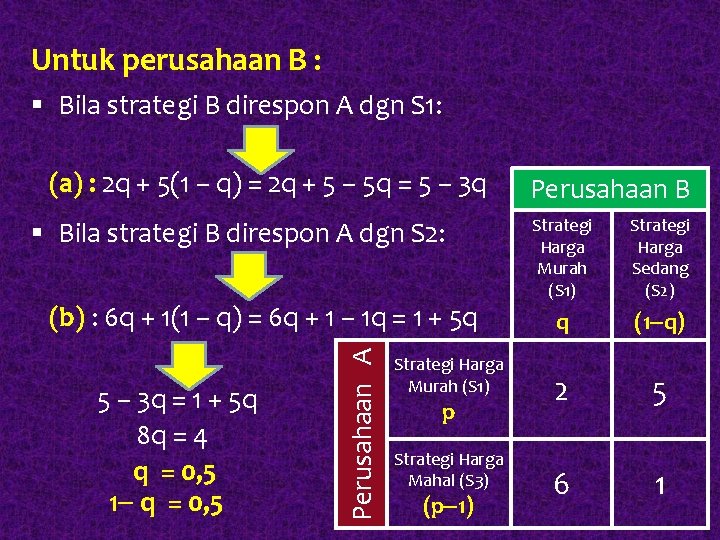
Untuk perusahaan B : § Bila strategi B direspon A dgn S 1: (a) : 2 q + 5(1 – q) = 2 q + 5 – 5 q = 5 – 3 q § Bila strategi B direspon A dgn S 2: 5 – 3 q = 1 + 5 q 8 q = 4 q = 0, 5 1 q = 0, 5 Perusahaan A (b) : 6 q + 1(1 – q) = 6 q + 1 – 1 q = 1 + 5 q Strategi Harga Murah (S 1) p Strategi Harga Mahal (S 3) (p 1) Perusahaan B Strategi Harga Murah (S 1) Strategi Harga Sedang (S 2) q (1 q) 2 5 6 1

Masukkan nilai q dan (1 -q) pada persamaan (a) & (b) (a) : 2 q + 5(1 – q) = 2 q + 5 – 5 q = 5 – 3(0, 5) = 3, 5 (b) : 6 q + 1(1 – q) = 6 q + 1 – 1 q = 1 + 5(0, 5) = 3, 5 Kerugian minimal yg diharapkan sama, yaitu 3, 5 Pada langkah pertama kerugian minimal = 5 Dengan strategi ini B bisa menurunkan kerugian sebesar 1, 5.

Kesimpulan : § Strategi campuran memberikan saddle point = 3, 5. § Nilai ini memberikan peningkatan keuntungan A sebesar 3, 5 § dan mengakibatkan penurunan kerugian B sebesar 1, 5.

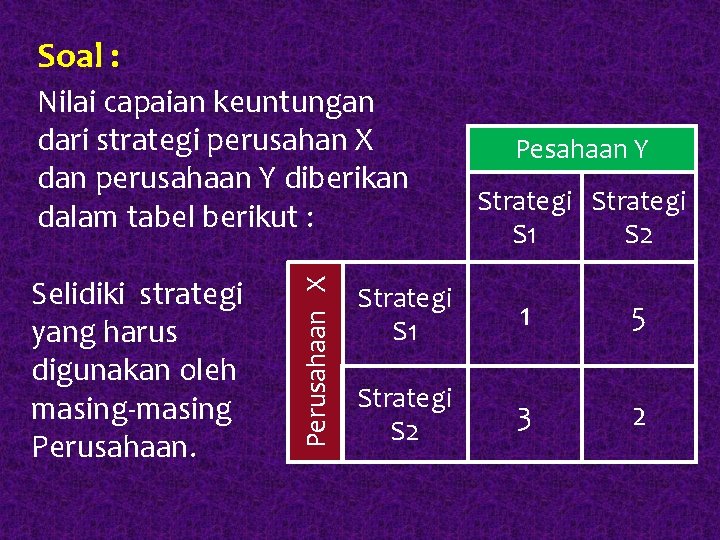
Soal : Selidiki strategi yang harus digunakan oleh masing-masing Perusahaan X Nilai capaian keuntungan dari strategi perusahan X dan perusahaan Y diberikan dalam tabel berikut : Pesahaan Y Strategi S 1 S 2 Strategi S 1 1 5 Strategi S 2 3 2

Terimakasih