ZEROSUM TOTAL CONFLICT GAMES Topic 5 The Payoff

ZERO-SUM (TOTAL CONFLICT) GAMES Topic #5

The Payoff Matrix for Zero-Sum Games • The payoff matrix for a Game Against Nature has only one number in each cell, – because Nature gets no payoffs. • The payoff matrix for a zero-conflict game (like Matching Pennies: Coordination Version) can also have only one number in each cell, – because each player gets the same payoff. – However, despite the redundancy, I put both payoffs in each cell in the zero-conflict matrices in Topic #4. • A payoff matrix for a zero-sum (or total conflict) game can also have only one number in each cell, – because one player’s payoff may be written as simply the negative of the other player’s payoff (the two payoffs therefore summing to zero). • By convention, the payoff the Row Player is put in the matrix, so – the objective of the Row Player is to maximize these payoffs, while – the objective of the Column Player is to minimize these payoffs.

Zero-Sum Games • You might at first think that, – because the anarchic international system is a mean and nasty place, – IR applications of Game Theory would pertain mostly to theory of zero-sum games. • But even nations that are bitter enemies have common interests, especially in a world with: – weapons of mass destruction (especially nuclear weapons) and – enduring conflicts (like the Cold War). • Variable-sum games (especially PD and Chicken) are generally much more relevant to IR than zero-sum games. • However, zero-sum games may be appropriate for analyzing specific conflict situations, such as particular battles in WWII. – We’ll focus on one such an example.

The Battle of the Bismarck Sea (March 1943) • The Japanese want to reinforce their army in New Guinea (to the west). • They must decide whether to send their troop and escort ships around the North or South coasts of New Britain Island. • US has aircraft west of the Island must to decide where to concentrate their reconnaissance flights, i. e. , mostly on the North or South side of the island. • The North side of the island is under quite heavy cloud cover, while the sky on the South side is mostly clear. • Once the US locates the Japanese ships, they will be attacked by US bombers. • Obviously, the US wants to maximize, and the Japanese want to minimize, the amount of time that the Japanese ships are exposed to attack.

The Battle of the Bismarck Sea (cont. ) • This situation somewhat resembles the D-Day Landings Game, with these differences: – here the US wants to “match, ” while the Japanese want to “mix”; and – the cloud cover on the North side of the island introduces an asymmetry that did not exist in the (very much simplified) D-Day Landings Game. • Choosing the cloud-covered Northern route is obviously appealing to the Japanese, – but its appeal to the Japanese is also evident to the US, so – maybe the Japanese should resist the appeal. • The nature of the game depends on the thickness of the cloud cover, which is reflected in the payoff matrix. – The following matrix reflects heavy cloud cover.

The Battle of the Bismarck Sea (cont. ) • The payoffs in the matrix indicate the number of days of US bombing of Japanese ships, – which are common knowledge to both players (at least to reasonable approximation), and which • the US wants to maximize, and • Japan wants to minimize. • What should each side choose to do? • This game can be almost, but not quite, “solved” on the basis of the Dominance Principle.

The Battle of the Bismarck Sea (cont. ) • Given these payoffs, the Japanese have a dominant strategy (sail North), – which they will presumably chose, based on the Corollary to the Dominance Principle: If you have a dominant strategy, use it. • This suggests another plausible corollary, which the US can use: – If the other player has a dominant strategy, use your best reply to that strategy. • Thus the US and Japan both choose north and the outcome is 2 days of US bombing, – which is (necessarily) a Nash equilibrium.

The Maximin (and Minimax) Principle • In either a Game Against Nature and a nonzero-sum game, the Maximin Principle may be overly cautious. – That is, a player who acts on the Maximin Principle may forfeit large payoffs that he could win by choosing a more aggressive strategy. • In a Game Against Nature, sticking to the Maximin Principle in effect assumes that Nature is always “out to get you. ” – While this sometimes feels like the case, nature is in fact indifferent to your fate. • In a nonzero-sum game, sticking to the Maximin Principle in effect assumes that the other player is always “out to get you. ” – But the other player has some interests in common with you, so in fact he is not always “out to get you. ”

Maximin and Minimax (cont. ) • But in a zero-sum game, the other player in effect is “out to get you. ” – More precisely, the other player is out to maximize his own payoff, • but (in a total-conflict situation) that is equivalent to being “out to get you, ” i. e. , trying to minimize your payoff. • So probably zero-sum games should be played – on the basis of the Maximin Principle by the Row Player, • whose goal is to maximize payoffs, and – on the basis of the (“mirror image”) Minimax Principle by the Column Player, • whose goal is to minimize payoffs.

The Maximin Payoff • The Row player (who wants to maximize) – looks at the worst thing that can happen (the minimum payoff or security level) when he plays each of his strategies and – chooses the strategy that gives the maximum of these minimum payoffs (the highest security level. • This is called the maximin payoff [with respect to “pure strategies” --- we will address this qualification later]. • In this way, the Row player wins at least his maximin payoff, regardless of what the Column player does.

The Minimax Payoff • Meanwhile the Column player (who wants to minimize) likewise – looks at the worst thing that can happen (the maximum payoff) when he plays each of his strategies and – chooses the strategy that gives the minimum of these maximum payoffs. • This is called the minimax payoff (with respect to “pure strategies”). • In this way, the Column player holds down Row’s payoff down to no more than this minimax payoff, regardless of what the Row player does.

Maximin and Minimax (cont. ) • Clearly it must always be true in zero-sum games that maximin payoff (for R) ≤ minimax payoff (for C). • That is, the payoff that Column can hold Row down to (regardless of what Row does) cannot (by definition) ever be less than the payoff Row can guarantee himself (regardless of what Column does). • Now suppose we have the limiting case, where maximin payoff (for R) = minimax payoff (for C) • In this event, the zero-sum game said to strictly determined. – The two players identify their maximin/minimax strategies and play them. – Neither player has any “wriggle-room” to try to outfox the other by trying “find out” his opponent’s strategy or deceive him about his own. – Moreover, neither player will ever regret his strategic choice, because the resulting outcome is always a (“pure-strategy”) Nash equilibrium.

Battle of the Bismarck Sea • The US thinks: “What is the greatest number of bombing days that we can guarantee ourselves, regardless of what the Japanese do? ” – That is, “what is the maximum of the minimum payoffs? ” – The answer is “ 2 days of bombing, ” guaranteed by choosing North. • The Japanese think: “What is the lowest number of days of bombing that we can hold the US down to, regardless of what they do? – That is, “what is the minimum of the maximum payoffs (to the US)? ” – The answer is “ 2 days of bombing, ” guaranteed by sailing North.

Strictly Determined Zero-Sum Games • So in this case: Maximin Payoff (for US) = Minimax Payoff (for JP) = 2 days of bombing – That is, what the US can guarantee itself is exactly equal to what the Japanese can hold the US down to. • So the Battle of the Bismarck Sea is a strictly determined zero -sum game.

The Battle of the Bismarck Sea (cont. ) • Strict determination means that the Japanese will sail North even though they must expect the US to concentrate its reconnaissance effort in the North. – The Japanese cannot gain by “fooling” the US by going South because, with no cloud cover, even a small US reconnaissance effort will find them more quickly than if they sail North • Note that if the US somehow had to direct its reconnaissance effort entirely to the North or South, the game would be quite different, – because then the Japanese would get through unscathed if the US failed to “match. ”

Strictly Determined Zero-Sum Games (cont. ) • A zero-sum game may be strictly determined even if neither player has a dominant strategy, – as is illustrated by the payoff matrix above. • The minimax/maximin payoff always a Nash equilibium. – In the special context of zero-sum games, this payoff is sometimes called a saddle point. – Examination of the maximin row and minimax column indicates that rationale for this name.

Strictly Determined Zero-Sum Games (cont. ) • A player may have more than one maximin (or minimax) strategy. – Therefore, a zero-sum game may have multiple equilibrium payoffs (saddlepoints). • Does this present a problem for strategy selection, – as it does in pure Coordination Games and the Battle of the Sexes? • No: suppose that s 1 and s 3 are both maximin strategies for Row, and c 1 and c 4 are both minimax strategies for Column. Since s 1 is maximin, p 11 ≥ p 31. But since s 3 is also maximim, p 31 ≥ p 11. • So p 11 = p 31. – Generalizing the argument: p 11 = p 31 = p 14 = p 34, – – • So Maxmin/minmax strategies are interchangeable and equivalent.

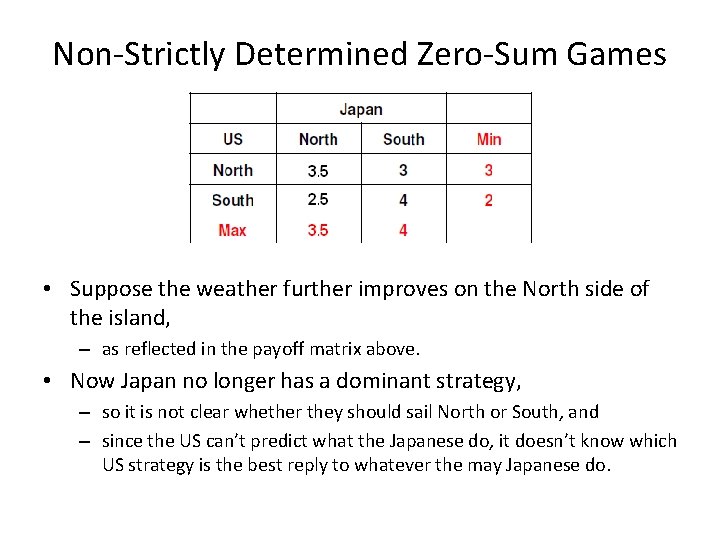
Strictly Determined Zero-Sum Games (cont. ) • Are all zero sum games strictly determined? • No. Consider what happens when the cloud cover on the north side of the island become less dense. – The effect is to expose the Japanese to more days of US bombing in the event they sail North. • In the matrix above, – “sail North” remains just barely a (weakly) dominant for the Japanese, and – the game remains just barely strictly determined.

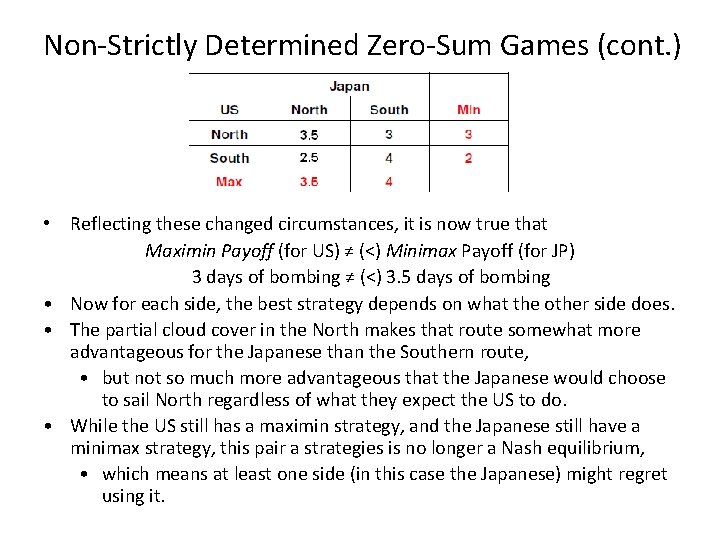
Non-Strictly Determined Zero-Sum Games • Suppose the weather further improves on the North side of the island, – as reflected in the payoff matrix above. • Now Japan no longer has a dominant strategy, – so it is not clear whether they should sail North or South, and – since the US can’t predict what the Japanese do, it doesn’t know which US strategy is the best reply to whatever the may Japanese do.

Non-Strictly Determined Zero-Sum Games (cont. ) • Reflecting these changed circumstances, it is now true that Maximin Payoff (for US) ≠ (<) Minimax Payoff (for JP) 3 days of bombing ≠ (<) 3. 5 days of bombing • Now for each side, the best strategy depends on what the other side does. • The partial cloud cover in the North makes that route somewhat more advantageous for the Japanese than the Southern route, • but not so much more advantageous that the Japanese would choose to sail North regardless of what they expect the US to do. • While the US still has a maximin strategy, and the Japanese still have a minimax strategy, this pair a strategies is no longer a Nash equilibrium, • which means at least one side (in this case the Japanese) might regret using it.

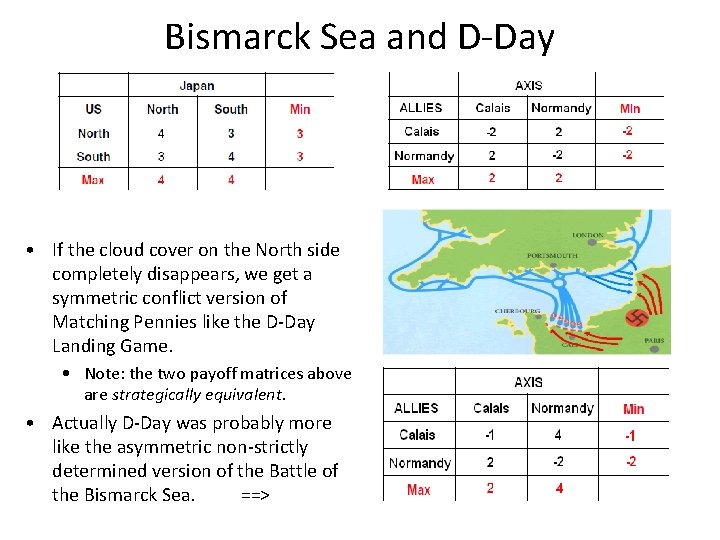
Bismarck Sea and D-Day • If the cloud cover on the North side completely disappears, we get a symmetric conflict version of Matching Pennies like the D-Day Landing Game. • Note: the two payoff matrices above are strategically equivalent. • Actually D-Day was probably more like the asymmetric non-strictly determined version of the Battle of the Bismarck Sea. ==>

Pure vs. Mixed Strategies • In the asymmetric but non-strictly determined version of both the Battle of the Bismarck Sea and D-Day Landings, we have: Maximin Payoff (for Row) < Minimax Payoff (for Column) • Is there any way that the Row (or Column) player can increase his maximin (or minimax) payoffs, so that the “gap” between the two payoffs can reduced or closed entirely? • Yes, they can do this by employing “mixed strategies. ” • A pure strategy is a complete plan of action for playing a game. • In the very simple payoff matrix games we have examined thus far, • a (pure) strategy for the row player is simply a row in the matrix, and • a (pure) strategy for the column player is simply a column in the matrix. • A mixed strategy is a probability distribution (or lottery) over pure strategies. • For example, if a player has two pure strategies s 1 and s 2, a mixed strategy would be: • {play s 1 with a probability of. 75 and play s 2 with a probability of. 25}.

Pure vs. Mixed Strategies (cont. ) • In analyzing mixed strategies, we must assume that the payoffs represent cardinal utility, – for example, that a player is indifferent between • a payoff of +1 for sure, and • a lottery ticket giving – a. 5 chance of a payoff of +2 and – a. 5 chance of a payoff of 0. • Thus, if payoffs in the Battle of the Bismarck Sea correspond to days of bombing (though they need not) and if we calculate payoffs from mixed strategies, – we are assuming that both the US and Japan are indifferent between • one day of bombing, and • a lottery ticket giving – a. 5 chance of a payoff of two days of bombing and – a. 5 chance of no bombing.

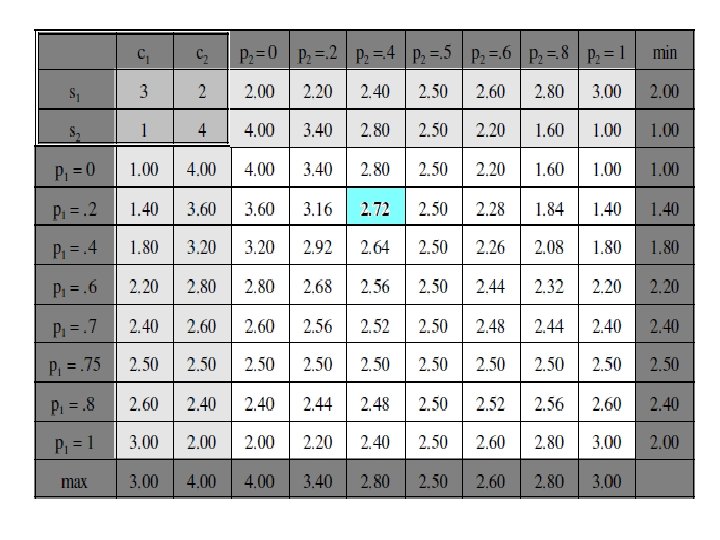
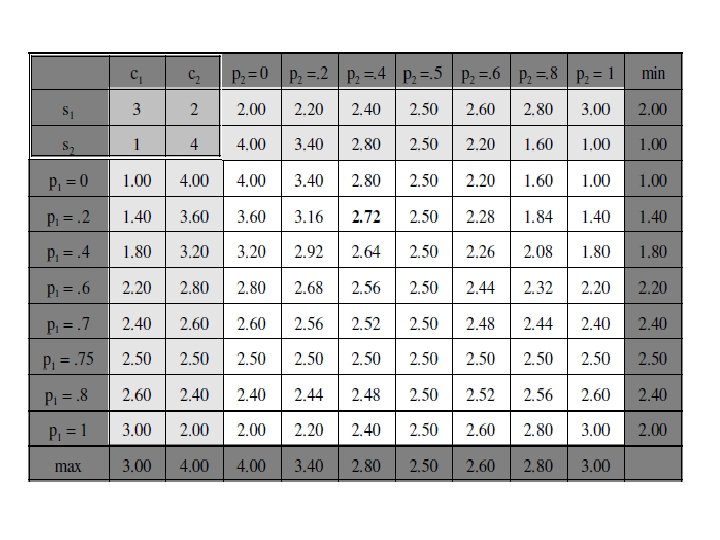
Pure vs. Mixed Strategies (cont. ) • The following slide shows a payoff matrix for a 2 x 2 (with respect to pure strategies) non-strictly determined zero sum game, – which has been expanded to include a sample of mixed strategies for each player as well. • Darkest shading: Labels for rows and columns • Medium shading: Basic 2 × 2 payoff matrix (for pure strategies) • Lightest shading: Expected payoffs for pure strategies vs. mixed strategies • No shading: Expected payoffs for mixed strategies vs. mixed strategies

Pure vs. Mixed Strategies (cont. ) • Consider the payoff matrix on the following slide. – Each player has two pure strategies: • s 1 and s 2 for the Row player, and • s 1 and c 2 for the column player. – The 2 x 2 pure strategy game is shown in the upper-left corner. – The game is not strictly determined, since (with respect to pure strategies: Maximin Payoff (for Row) < Minimax Payoff (for Column) 2<3 • The remainder of the matrix show payoffs for various combinations of mixed strategies, where • p 1 is the probability that Row chooses s 1 and [and (1 -p 1) is the probability Row chooses s 2] and • p 2 is the probability that Column chooses c 1 and [and (1 -p 2) is the probability Row chooses c 2]. • “Degenerate” mixed strategies (where p = 0 or p =1) are equivalent to pure strategies.

Mixed Strategy Payoffs. • The expected payoffs from each pair of mixed strategies can be calculated straightforwardly, – for example, for the mixed strategy pair (p 1 =. 2, p 2 =. 4):

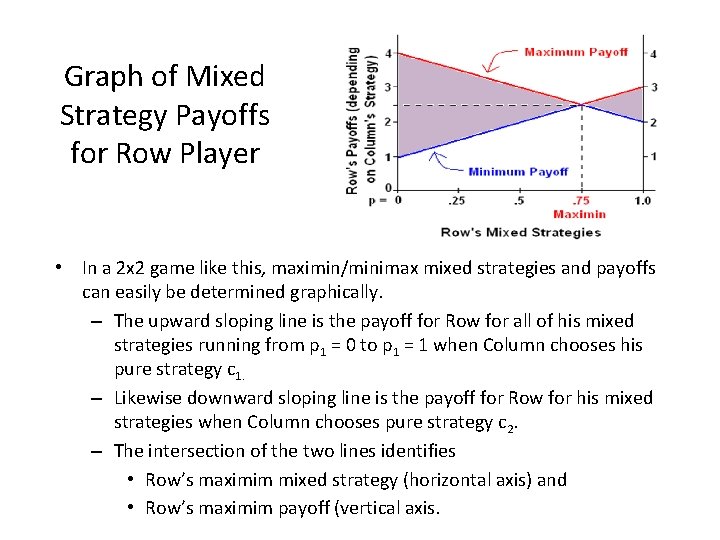
Graph of Mixed Strategy Payoffs for Row Player • In a 2 x 2 game like this, maximin/minimax mixed strategies and payoffs can easily be determined graphically. – The upward sloping line is the payoff for Row for all of his mixed strategies running from p 1 = 0 to p 1 = 1 when Column chooses his pure strategy c 1. – Likewise downward sloping line is the payoff for Row for his mixed strategies when Column chooses pure strategy c 2. – The intersection of the two lines identifies • Row’s maximim mixed strategy (horizontal axis) and • Row’s maximim payoff (vertical axis.

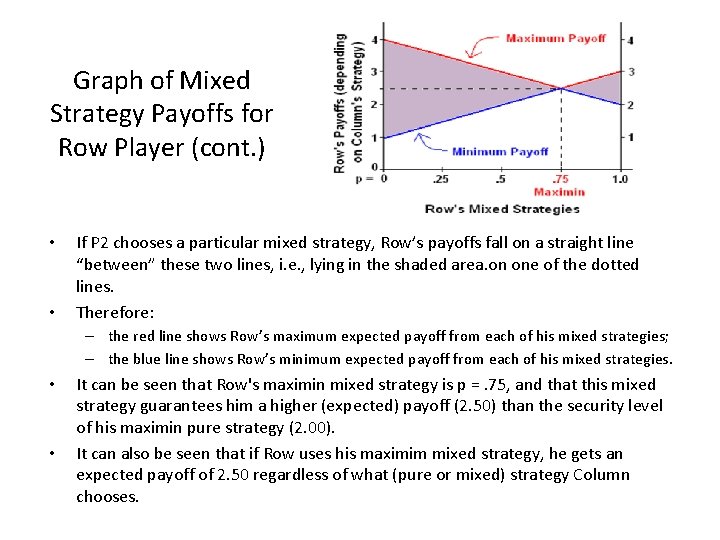
Graph of Mixed Strategy Payoffs for Row Player (cont. ) • • If P 2 chooses a particular mixed strategy, Row’s payoffs fall on a straight line “between” these two lines, i. e. , lying in the shaded area. on one of the dotted lines. Therefore: – the red line shows Row’s maximum expected payoff from each of his mixed strategies; – the blue line shows Row’s minimum expected payoff from each of his mixed strategies. • • It can be seen that Row's maximin mixed strategy is p =. 75, and that this mixed strategy guarantees him a higher (expected) payoff (2. 50) than the security level of his maximin pure strategy (2. 00). It can also be seen that if Row uses his maximim mixed strategy, he gets an expected payoff of 2. 50 regardless of what (pure or mixed) strategy Column chooses.

Mixed Strategy Payoffs • Notice that Row can increase his security level of expected payoffs above his pure-strategy maximin of 2. 00 by using mixed strategies. – For example, Row’s mixed strategy p 1 =. 6 has a security level of 2. 20. * – The mixed strategy p 1 =. 75 gives Row his highest security level, i. e. , the maximum of his minimum payoffs, of 2. 50. – The mixed strategy p 1 =. 75 also gives Row the minimum of his maximum payoffs, i. e. , also 2. 50. • Put otherwise, if Row uses his maximim mixed strategy p 1 =. 75, Row’s payoff is the same (i. e. , 2. 50) regardless of what (pure or mixed) strategy Column uses. ~~~~~~~~~~~~~~~~~~ * Note that the security level of a mixed strategy is the minimum expected payoff – with respect to all (pure or mixed) strategies that the other player chooses, – not with respect to all of the outcome of the lottery of payoffs that any mixed strategy entails. • In any particular play of the game, Row’s actual payoff is either 1, or 2, or 3, or 4.

Mixed Strategy Payoffs • Likewise, the Column player can hold Row’s level of expected payoff below this pure-strategy minimax of 3. 00 by using mixed strategies. – The mixed strategy p 2 =. 50 gives Row the minimum of maximum payoffs, i. e. , 2. 50. • Moreover, if Row uses this minimax mixed strategy p 1 =. 50, Row’s payoff is the same regardless of what (pure or mixed) strategy Row uses. • If a player has three (or more) pure strategies, his maximin (or minimax) mixed strategy – may place zero probability on one (or more) of his pure strategies, and – in particular, his maximim (or minimax) mixed strategy always puts zero probability on any (“sequentially”) dominated pure strategy.

The Minimax Theorem • It turns out that, in every two player zero-sum game, – when the strategy sets of both players are expanded to include all possible mixtures of their pure strategies, we return to the equality maximin payoff (for Row) = minimax payoff (for Column) that is true of strictly determined games with respect to pure strategies only. • Moreover, when the players use their maximin and minimax (respectively) mixed strategies, the result is a Nash equilibrium, i. e. , – given the strategy choice of the other player, neither player can do better by changing to any other pure or mixed strategy. • The proof of these claims is called the Minimax Theorem, – which is regarded as the fundamental theorem of game theory. • In this sense, all two-player zero-sum games are “non-strictly determined. ”

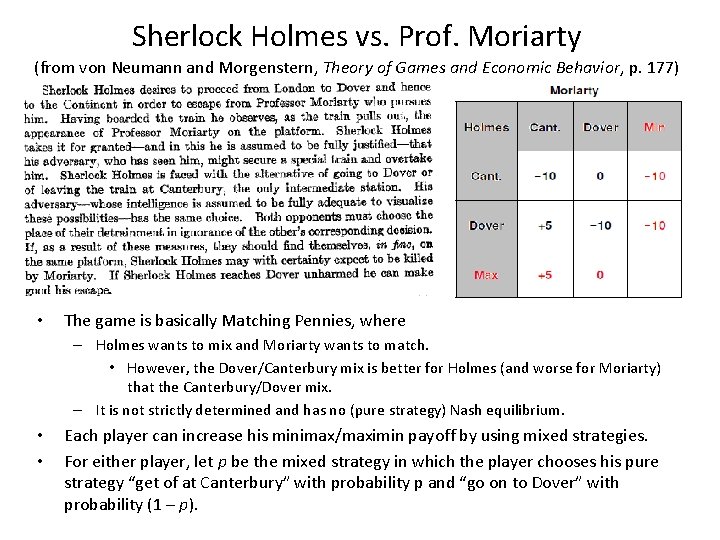
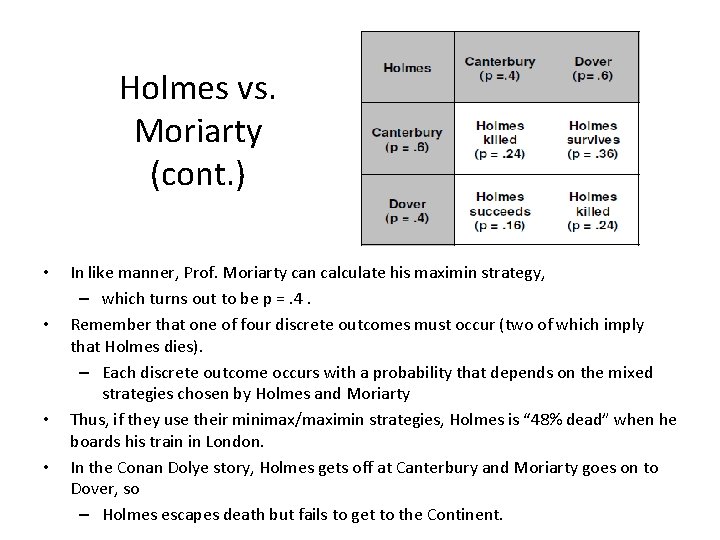
Sherlock Holmes vs. Prof. Moriarty (from von Neumann and Morgenstern, Theory of Games and Economic Behavior, p. 177) • The game is basically Matching Pennies, where – Holmes wants to mix and Moriarty wants to match. • However, the Dover/Canterbury mix is better for Holmes (and worse for Moriarty) that the Canterbury/Dover mix. – It is not strictly determined and has no (pure strategy) Nash equilibrium. • • Each player can increase his minimax/maximin payoff by using mixed strategies. For either player, let p be the mixed strategy in which the player chooses his pure strategy “get of at Canterbury” with probability p and “go on to Dover” with probability (1 – p).

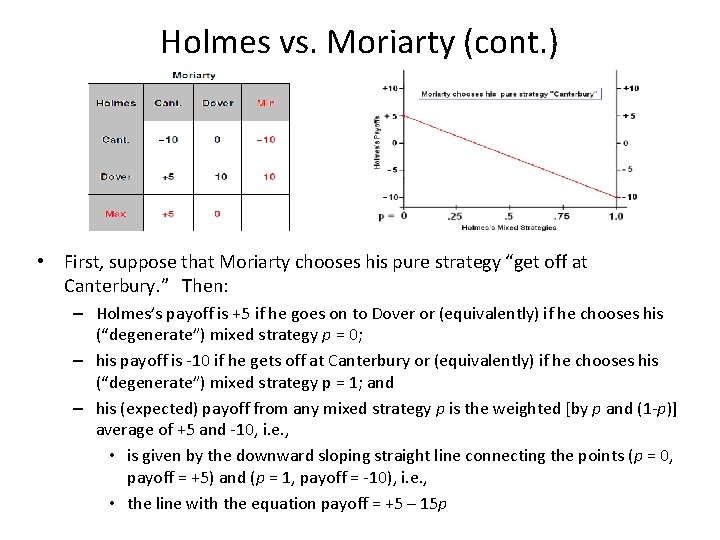
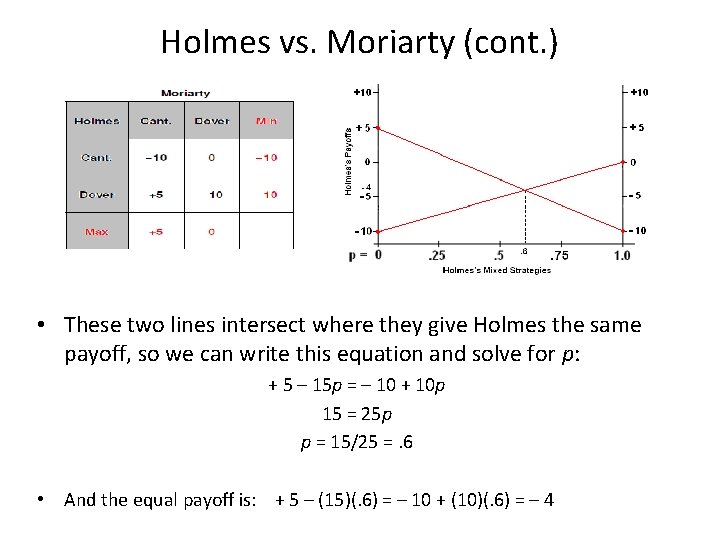
Holmes vs. Moriarty (cont. ) • First, suppose that Moriarty chooses his pure strategy “get off at Canterbury. ” Then: – Holmes’s payoff is +5 if he goes on to Dover or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 0; – his payoff is -10 if he gets off at Canterbury or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 1; and – his (expected) payoff from any mixed strategy p is the weighted [by p and (1 -p)] average of +5 and -10, i. e. , • is given by the downward sloping straight line connecting the points (p = 0, payoff = +5) and (p = 1, payoff = -10), i. e. , • the line with the equation payoff = +5 – 15 p

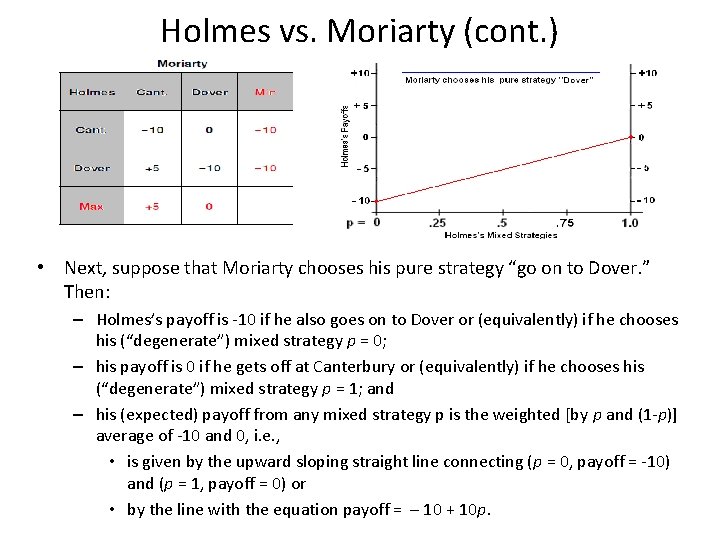
Holmes vs. Moriarty (cont. ) • Next, suppose that Moriarty chooses his pure strategy “go on to Dover. ” Then: – Holmes’s payoff is -10 if he also goes on to Dover or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 0; – his payoff is 0 if he gets off at Canterbury or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 1; and – his (expected) payoff from any mixed strategy p is the weighted [by p and (1 -p)] average of -10 and 0, i. e. , • is given by the upward sloping straight line connecting (p = 0, payoff = -10) and (p = 1, payoff = 0) or • by the line with the equation payoff = – 10 + 10 p.

Holmes vs. Moriarty (cont. ) • These two lines intersect where they give Holmes the same payoff, so we can write this equation and solve for p: + 5 – 15 p = – 10 + 10 p 15 = 25 p p = 15/25 =. 6 • And the equal payoff is: + 5 – (15)(. 6) = – 10 + (10)(. 6) = – 4

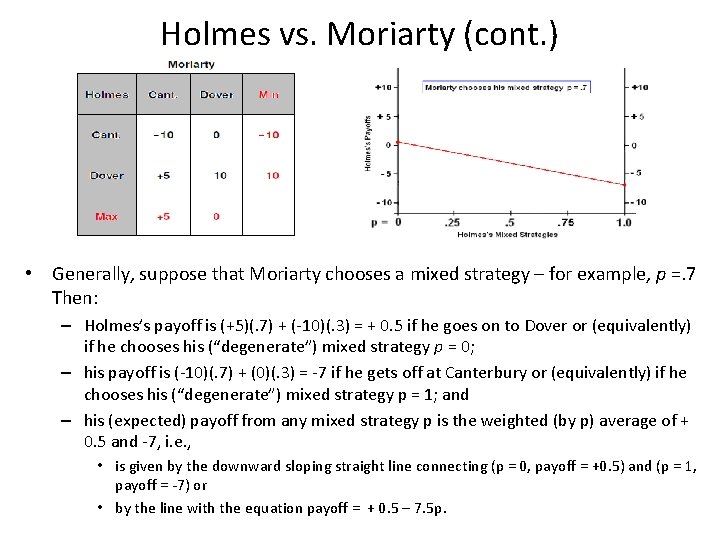
Holmes vs. Moriarty (cont. ) • Generally, suppose that Moriarty chooses a mixed strategy – for example, p =. 7 Then: – Holmes’s payoff is (+5)(. 7) + (-10)(. 3) = + 0. 5 if he goes on to Dover or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 0; – his payoff is (-10)(. 7) + (0)(. 3) = -7 if he gets off at Canterbury or (equivalently) if he chooses his (“degenerate”) mixed strategy p = 1; and – his (expected) payoff from any mixed strategy p is the weighted (by p) average of + 0. 5 and -7, i. e. , • is given by the downward sloping straight line connecting (p = 0, payoff = +0. 5) and (p = 1, payoff = -7) or • by the line with the equation payoff = + 0. 5 – 7. 5 p.

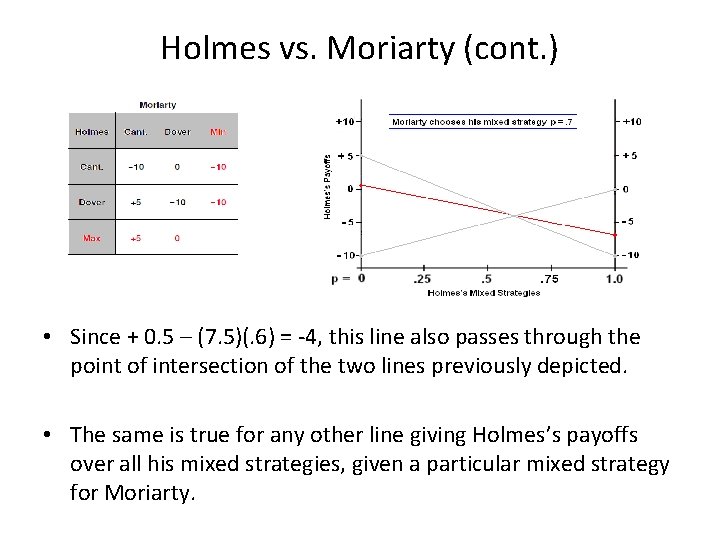
Holmes vs. Moriarty (cont. ) • Since + 0. 5 – (7. 5)(. 6) = -4, this line also passes through the point of intersection of the two lines previously depicted. • The same is true for any other line giving Holmes’s payoffs over all his mixed strategies, given a particular mixed strategy for Moriarty.

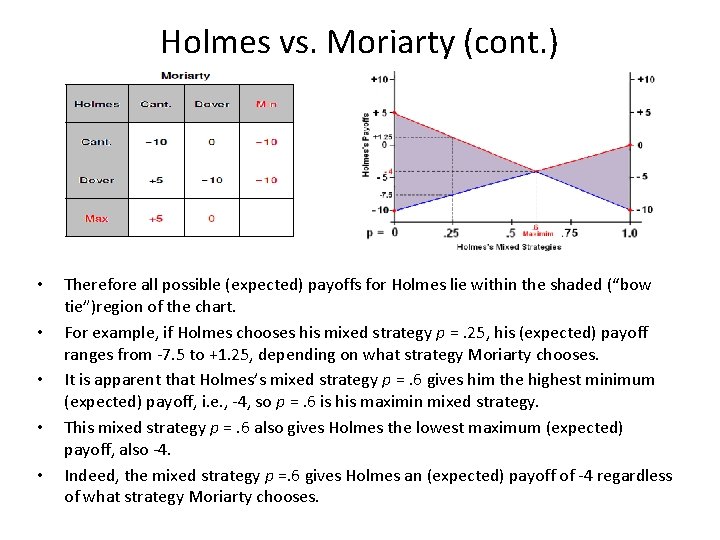
Holmes vs. Moriarty (cont. ) • • • Therefore all possible (expected) payoffs for Holmes lie within the shaded (“bow tie”)region of the chart. For example, if Holmes chooses his mixed strategy p =. 25, his (expected) payoff ranges from -7. 5 to +1. 25, depending on what strategy Moriarty chooses. It is apparent that Holmes’s mixed strategy p =. 6 gives him the highest minimum (expected) payoff, i. e. , -4, so p =. 6 is his maximin mixed strategy. This mixed strategy p =. 6 also gives Holmes the lowest maximum (expected) payoff, also -4. Indeed, the mixed strategy p =. 6 gives Holmes an (expected) payoff of -4 regardless of what strategy Moriarty chooses.

Holmes vs. Moriarty (cont. ) • • In like manner, Prof. Moriarty can calculate his maximin strategy, – which turns out to be p =. 4. Remember that one of four discrete outcomes must occur (two of which imply that Holmes dies). – Each discrete outcome occurs with a probability that depends on the mixed strategies chosen by Holmes and Moriarty Thus, if they use their minimax/maximin strategies, Holmes is “ 48% dead” when he boards his train in London. In the Conan Dolye story, Holmes gets off at Canterbury and Moriarty goes on to Dover, so – Holmes escapes death but fails to get to the Continent.

Minimax Mixed Strategies • If a player has three (or more) pure strategies, calculating maximin (or minimax) mixed strategies becomes much more complicated. • A maximin (or minimax) mixed strategy – may place zero probability on one (or more) of his pure strategies, and – in particular, • his maximim (or minimax) mixed strategy always puts zero probability on any [“sequentially”] dominated pure strategy, and • all the probability on a dominant strategy.

The Minimax Theorem • It turns out that, in every two player zero-sum game, – when the strategy sets of both players are expanded to include all possible mixtures of their pure strategies, we return to the equality maximin payoff (for Row) = minimax payoff (for Column) that is true of strictly determined games with respect to pure strategies only. • Moreover, when the players use their maximin and minimax (respectively) mixed strategies, the result is a Nash equilibrium, i. e. , – given the strategy choice of the other player, neither player can do better by changing to any other pure or mixed strategy. • The proof of these claims is called the Minimax Theorem, – which is regarded as the fundamental theorem of game theory. • In this sense, all two-player zero-sum games are “non-strictly determined. ”

John Nash (“A Beautiful Mind”) • Nash Theorem: Every game (two players or many players, zero-sum or non-zero sum) has at least one mixed strategy Nash equilibrium. – In a two-player zero-sum games, all such equilibria give the same payoff. – But in the general case • different equilibria may give different payoffs, – e. g. , Battle of Sexes, Chicken, • Indeed, there may be a huge number of equilibria.

Interpretation of Mixed Strategies • In a “single-shot” game, it is impossible to tell whether a player is using a mixed strategy. • For example, on each pitch a baseball pitcher has (at least) two pure strategies: – s 1 (throw a fast ball) and – s 2 (throw curve ball). • Suppose that on a particular pitch, the pitcher actually throws a curve ball • Neither an observer nor the batter can tell whether the pitcher chose – the pure strategy s 2 or – some mixed strategy (that put a non-zero probability on s 2). • But if the “game” (a single pitch) is repeated many times using the same mixed strategy, – a mixed strategy such as {play s 1 with a probability of. 75 and play s 2 with a probability of. 25} – reveals itself as {P 1 plays s 1 75% of the time and plays s 2 25% of the time} (but in no predictable sequence). • Reread Dixit and Nalebuff, Chapter 7 on zero-sum duels between baseball pitchers and batters or between tennis players with this discussion in mind.

Applications of Mixed Strategies • One of the most common actual uses of mixed strategies is in (repeated) Inspector vs. Evader games, – which are non-strictly determined zero-sum games in which • the Inspector wants to match, and • the Evader wants to mix. • The most familiar example may be the timing of police patrols, – in which it clear that police should not patrol at regular (predictable) intervals but should “mix it up. ” • Other examples: – unannounced quizzes; – proctoring exams; – weapons inspections to enforce arms control agreements (or sanctions); – WWII contests between German U-boats and Allied anti-submarine patrols. • “Operations researchers” actually calculated optimal mixed strategies.