Zerosum Games The Essentials of a Game Extensive

Zero-sum Games • • The Essentials of a Game Extensive Game Matrix Game Dominant Strategies Prudent Strategies Solving the Zero-sum Game The Minimax Theorem

The Essentials of a Game 1. Players: We require at least 2 players (Players choose actions and receive payoffs. ) 2. Actions: Player chooses i from finite a set actions, of=S {s 1, s 2, …. . , sn}. Player j chooses from a finite set of actions T = {t 1, t 2, ……, tm}. 3. Payoffs: Wedefine. Pi(s, t)asthepayofftoplayeri, if. Playeri chooses s and player j chooses t. We require that ZERO-SUM Pi(s, t) + Pj(s, t) = 0 for all combinations of s and t. What 4. choosing actions.

The Essentials of a Game 4. Information: What players know (believe) when choosing actions. Perfect Information: Players know • their own payoffs Common Knowledge • other player(s) payoffs • the history of the game, including other(s) current action* *Actions are sequential (e. g. , chess, tic-tac-toe).

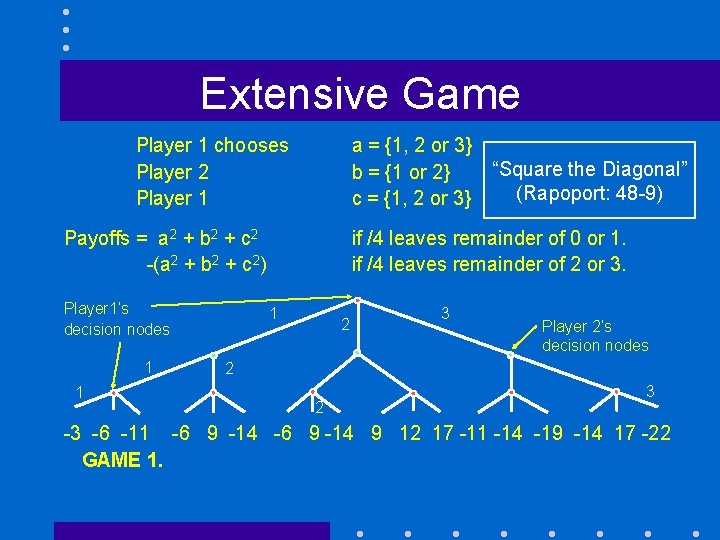
Extensive Game Player 1 chooses Player 2 Player 1 a = {1, 2 or 3} “Square the Diagonal” b = {1 or 2} (Rapoport: 48 -9) c = {1, 2 or 3} Payoffs = a 2 + b 2 + c 2 -(a 2 + b 2 + c 2) Player 1’s decision nodes 1 1 if /4 leaves remainder of 0 or 1. if /4 leaves remainder of 2 or 3. 1 2 3 Player 2’s decision nodes 2 2 3 -3 -6 -11 -6 9 -14 9 12 17 -11 -14 -19 -14 17 -22 GAME 1.

Extensive Game How should the game be played? Solution: a set of “advisable” strategies, one for each player. Start at the final decision nodes (in red) 1 1 1 2 3 Backwards-induction 2 2 3

Extensive Game How should the game be played? Solution: a set of “advisable” strategies, one for each player. Player 1’s advisable strategy in red 1 1 1 2 3 Player 2’s advisable strategy in green 2 2 3

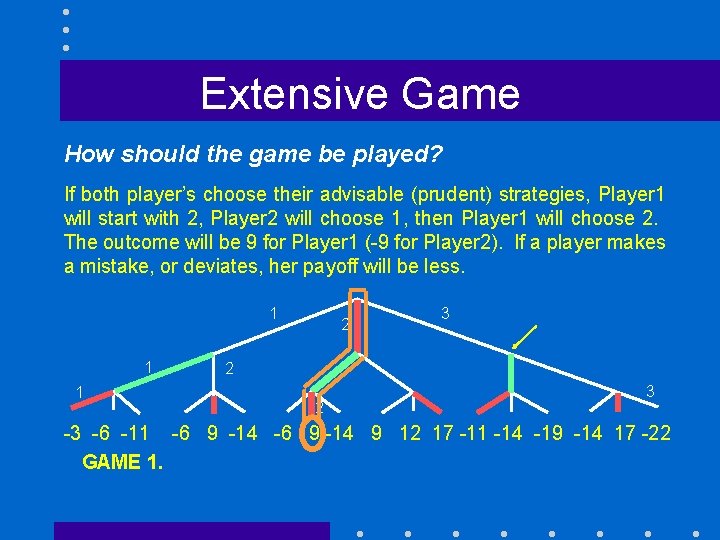
Extensive Game How should the game be played? If both player’s choose their advisable (prudent) strategies, Player 1 will start with 2, Player 2 will choose 1, then Player 1 will choose 2. The outcome will be 9 for Player 1 (-9 for Player 2). If a player makes a mistake, or deviates, her payoff will be less. 1 1 1 2 3 2 2 3 -3 -6 -11 -6 9 -14 9 12 17 -11 -14 -19 -14 17 -22 GAME 1.

Extensive Game A Clarification: Rapoport (pp. 49 -53) claims Player 1 has 27 strategies. However, if we consider inconsistent strategies, the actual number of strategies available to Player 1 is 37 = 2187. An inconsistent strategy includes actions at decision nodes that would not be reached by correct implementation at earlier nodes, i. e. , could only be reached by mistake. Since we can think of a strategy as a set of instructions (or program) given to an agent or referee (or machine) to implement, a complete strategy must include instructions for what to do after a mistake is made. This greatly expands the number of strategies available, though the essence of Rapoport’s analysis is correct.

Extensive Game Complete Information: Players know their own payoffs; other player(s) payoffs; history of the game excluding other(s) current action* *Actions are simultaneous 1 1 1 2 3 Information Sets 2 2 3 -3 -6 -11 -6 9 -14 9 12 17 -11 -14 -19 -14 17 -22 GAME 1.

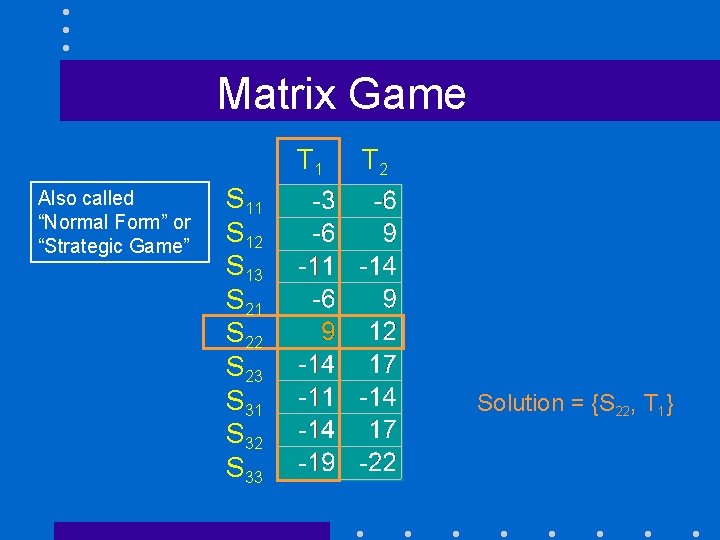
Matrix Game T 1 Also called “Normal Form” or “Strategic Game” S 11 S 12 S 13 S 21 S 22 S 23 S 31 S 32 S 33 T 2 Solution = {S 22, T 1}

Dominant Strategies Definition Dominant Strategy: a strategy that is best no matter what the opponent(s) choose(s). T 1 T 2 T 3 S 1 -3 0 1 S 1 -3 0 -10 S 2 -1 5 2 S 3 -2 2 0 S 3 -2 -4 0

Dominant Strategies Definition Dominant Strategy: a strategy that is best no matter what the opponent(s) choose(s). T 1 T 2 T 3 S 1 -3 0 1 S 1 -3 0 -10 S 2 -1 5 2 S 3 -2 2 0 S 3 -2 -4 0 Sure Thing Principle: If you have a dominant strategy, use it!

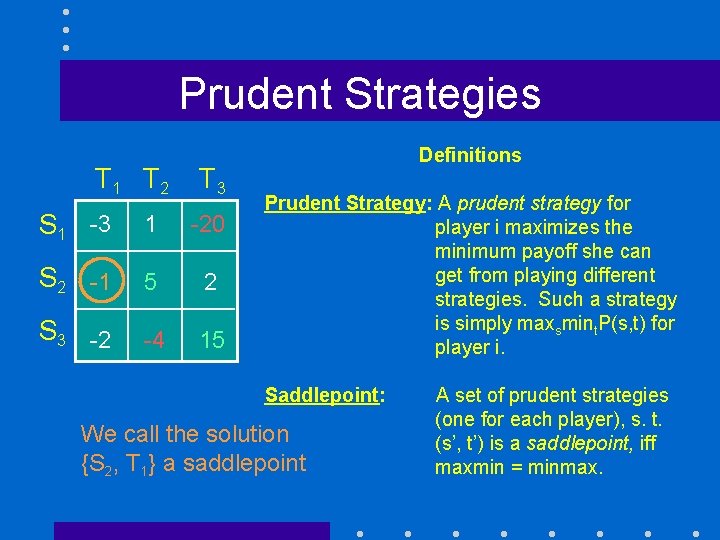
Prudent Strategies T 1 T 2 T 3 S 1 -3 1 -20 S 2 -1 5 2 S 3 -2 -4 15 Definitions Prudent Strategy: A prudent strategy for player i maximizes the minimum payoff she can get from playing different strategies. Such a strategy is simply maxsmint. P(s, t) for player i. Player 1’s worst payoffs for each strategy are in red.

Prudent Strategies T 1 T 2 T 3 S 1 -3 1 -20 S 2 -1 5 2 S 3 -2 -4 15 Definitions Prudent Strategy: A prudent strategy for player i maximizes the minimum payoff she can get from playing different strategies. Such a strategy is simply maxsmint. P(s, t) for player i. Player 2’s worst payoffs for each strategy are in green.

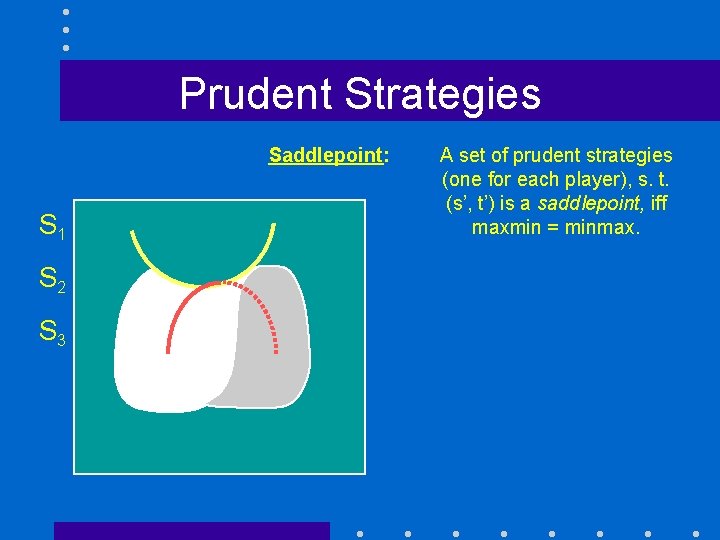
Prudent Strategies T 1 T 2 T 3 S 1 -3 1 -20 S 2 -1 5 2 S 3 -2 -4 15 Definitions Prudent Strategy: A prudent strategy for player i maximizes the minimum payoff she can get from playing different strategies. Such a strategy is simply maxsmint. P(s, t) for player i. Saddlepoint: We call the solution {S 2, T 1} a saddlepoint A set of prudent strategies (one for each player), s. t. (s’, t’) is a saddlepoint, iff maxmin = minmax.

Prudent Strategies Saddlepoint: S 1 -3 1 -20 S 2 -1 5 2 S 3 -2 -4 15 A set of prudent strategies (one for each player), s. t. (s’, t’) is a saddlepoint, iff maxmin = minmax.

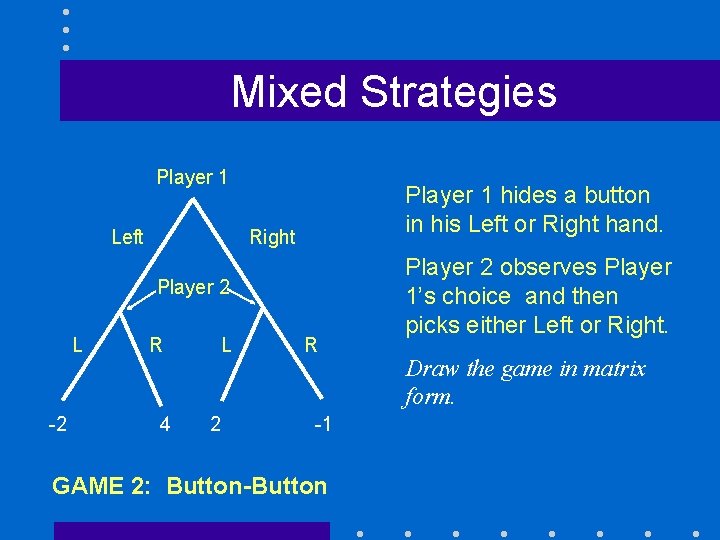
Mixed Strategies Player 1 Left Player 1 hides a button in his Left or Right hand. Right Player 2 L -2 R 4 L 2 R -1 GAME 2: Button-Button Player 2 observes Player 1’s choice and then picks either Left or Right. Draw the game in matrix form.

Mixed Strategies Player 1 Left Player 1 has 2 strategies; Player 2 has 4 strategies: Right Player 2 L -2 R 4 L 2 R -1 GAME 2: Button-Button L LL RL -2 RR LR 4 -2 4 R 2 -1 -1 2

Mixed Strategies Player 1 Left The game can be solve by backwards-induction. Player 2 will … Right Player 2 L -2 R 4 L 2 R -1 GAME 2: Button-Button L LL RL -2 RR LR 4 -2 4 R 2 -1 -1 2

Mixed Strategies Player 1 Left The game can be solve by backwards-induction. … therefore, Player 1 will: Right Player 2 L -2 R 4 L 2 R -1 GAME 2: Button-Button L LL RL -2 RR LR 4 -2 4 R 2 -1 -1 2

Mixed Strategies Player 1 Left Right L L R -2 4 2 -1 Player 2 L -2 R 4 L 2 R -1 GAME 2: Button-Button R What would happen if Player 2 cannot observe Player 1’s choice?

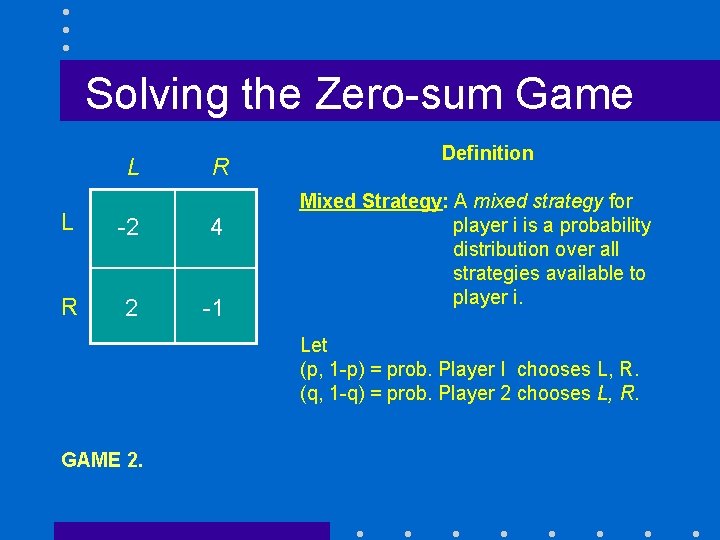
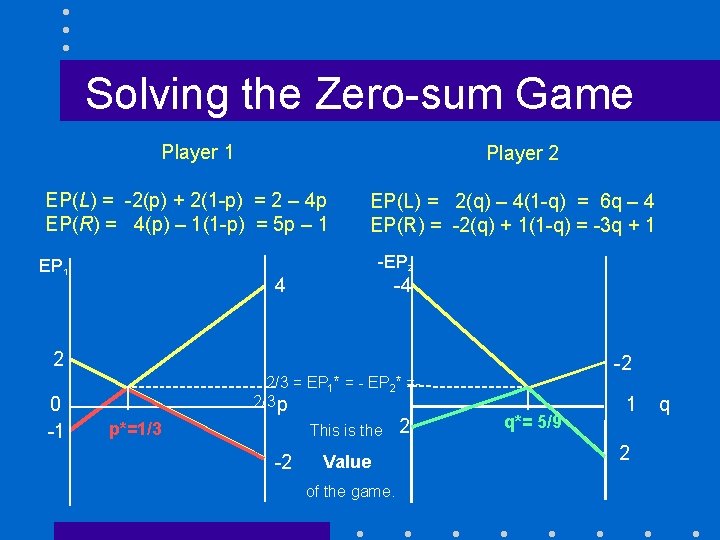
Solving the Zero-sum Game L R L -2 4 R 2 -1 Definition Mixed Strategy: A mixed strategy for player i is a probability distribution over all strategies available to player i. Let (p, 1 -p) = prob. Player I chooses L, R. (q, 1 -q) = prob. Player 2 chooses L, R. GAME 2.

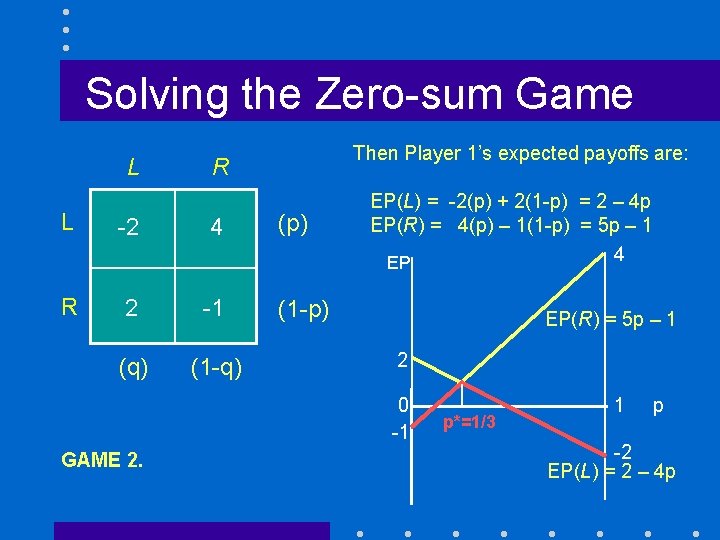
Solving the Zero-sum Game L Then Player 1’s expected payoffs are: R L -2 4 (p) R 2 -1 (1 -p) (q) (1 -q) EP(L) = -2(p) + 2(1 -p) = 2 – 4 p EP(R) = 4(p) – 1(1 -p) = 5 p – 1 4 EP EP(R) = 5 p – 1 2 0 -1 GAME 2. p*=1/3 1 p -2 EP(L) = 2 – 4 p

Solving the Zero-sum Game L L -2 Player 2’s expected payoffs are: R 4 (p) EP(L) = 2(q) – 4(1 -q) = 6 q – 4 EP(R) = -2(q) + 1(1 -q) = -3 q + 1 EP(L) = EP(R) R 2 -1 (q) (1 -q) GAME 2. (1 -p) => q* = 5/9

Solving the Zero-sum Game Player 1 Player 2 EP(L) = -2(p) + 2(1 -p) = 2 – 4 p EP(R) = 4(p) – 1(1 -p) = 5 p – 1 EP(L) = 2(q) – 4(1 -q) = 6 q – 4 EP(R) = -2(q) + 1(1 -q) = -3 q + 1 -EP 2 EP 1 4 -4 2 0 -1 2/3 = EP 1* = - EP 2* =2/3 p p*=1/3 This is the -2 Value of the game. 2 -2 q*= 5/9 1 2 q

Solving the Zero-sum Game Then Player 1’s expected payoffs are: L R L -2 4 (p) R 2 -1 (1 -p) (q) (1 -q) GAME 3. (Security) Value: the expected EP(T 1) = -2(p) + 2(1 -p) payoff when both (all) players play EP(T ) = 4(p) – 1(1 -p) prudent strategies. 2 EP(T 1) = EP(T 2) => p* = 1/3 Any deviation by an opponent leads to an. Player equal 2’s or greater payoff. And expected payoffs are: (V)alue = 2/3

The Minimax Theorem Von Neumann (1928) Every zero sum game has a saddlepoint (in pure or mixed strategies), s. t. , there exists a unique value, i. e. , an outcome of the game where maxmin = minmax.