Topos Theory for Musical Networks Guerino Mazzola U

Topos Theory for Musical Networks Guerino Mazzola U & ETH Zürich guerino@mazzola. ch www. encyclospace. org

Birkhäuser 2002 1365 pages, hardcover incl. CD-ROM US English ISBN 3 -7643 -5731 -2 Networks etc. —> PNM paper Mazzola + Andreatta

Wolfgang Graeser 1906 -1928 Bach‘s „Art of Fugue“ (1924) Eine kontrapunktische Form ist eine Menge von Mengen (von Tönen). A contrapuntal form is a set of sets (of tones).

Structures T N E M ! E E L R P A Processes M I W T F O S ON Gestures

Need recursive (possibly circular) combination of constructions such as „sequences of sets of curves of sets of chords“ etc. This leads to theory of denotators: —> concept architecture —> uses mathematical topos theory —> generalizes XML —> have implementation in Java

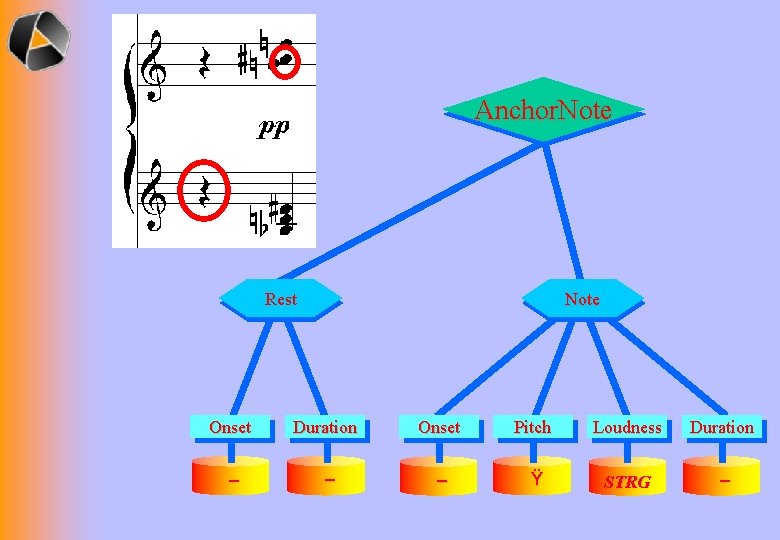
Anchor. Note Rest Note Onset Duration Onset Pitch Loudness Duration – – – Ÿ STRG –

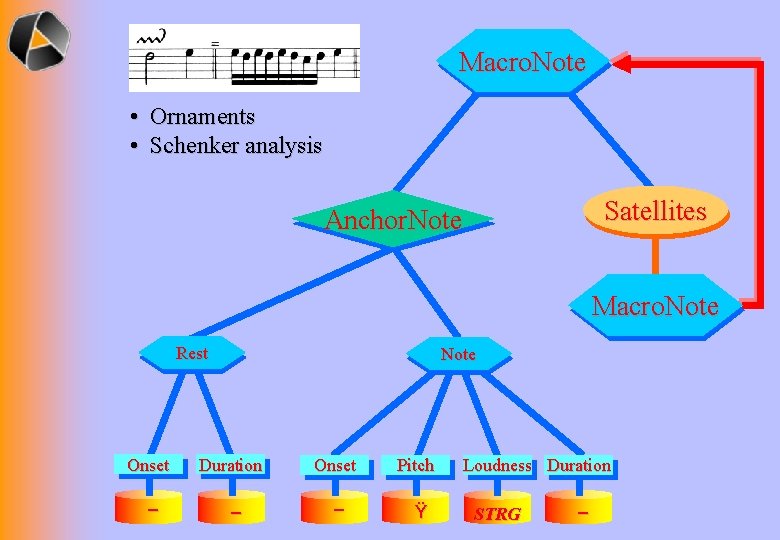
Macro. Note • Ornaments • Schenker analysis Satellites Anchor. Note Macro. Note Rest Onset – Note Duration – Onset Pitch – Ÿ Loudness Duration STRG –

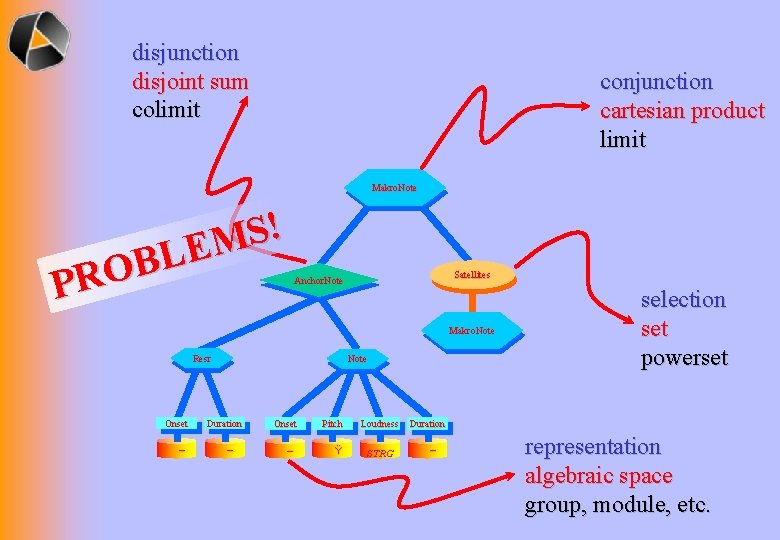
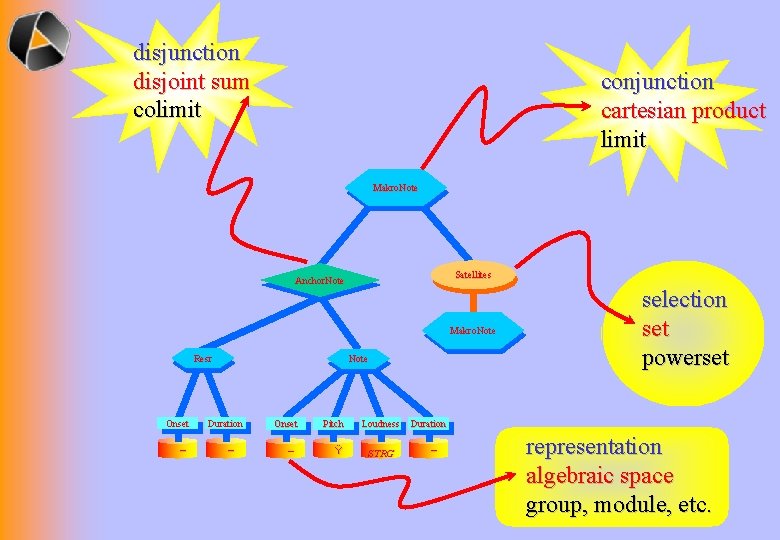
disjunction disjoint sum colimit conjunction cartesian product limit Makro. Note ! S M E L B O PR Satellites Anchor. Note Makro. Note Resr Onset – Note Duration – Onset – Pitch Ÿ Loudness STRG selection set powerset Duration – representation algebraic space group, module, etc.

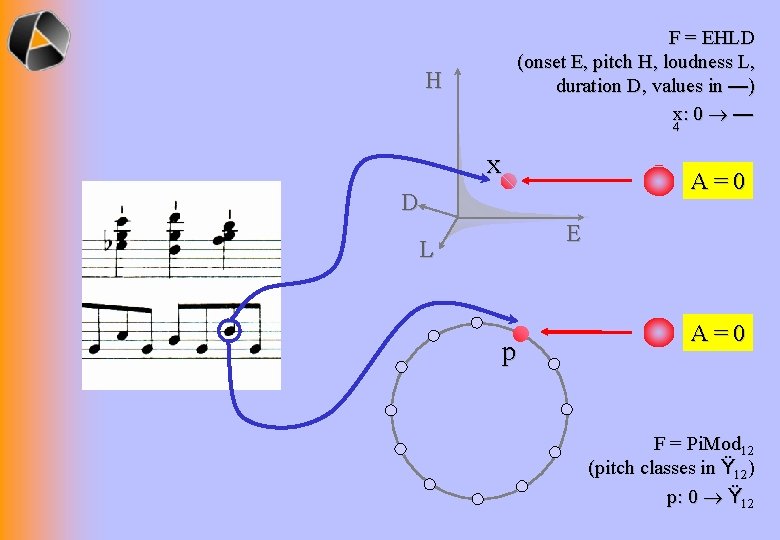
F = EHLD (onset E, pitch H, loudness L, duration D, values in —) x: 0 — H 4 x A=0 D E L p A=0 F = Pi. Mod 12 (pitch classes in Ÿ 12) p: 0 Ÿ 12

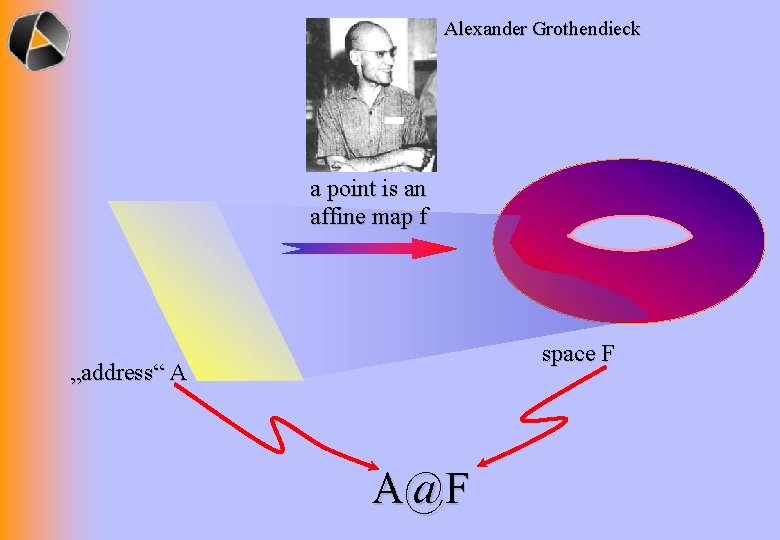
Alexander Grothendieck a point is an affine map f space F „address“ A A@F

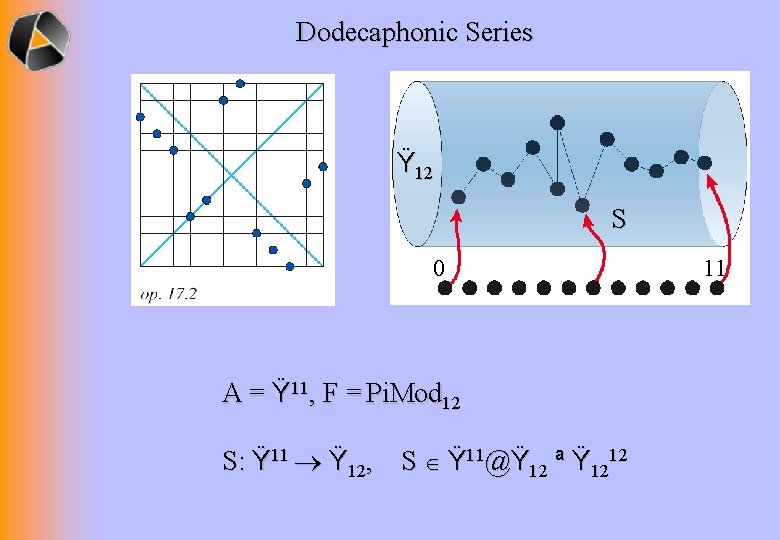
Dodecaphonic Series Ÿ 12 S 0 A = Ÿ 11, F = Pi. Mod 12 S: Ÿ 11 Ÿ 12, S Ÿ 11@Ÿ 12 ª Ÿ 1212 11

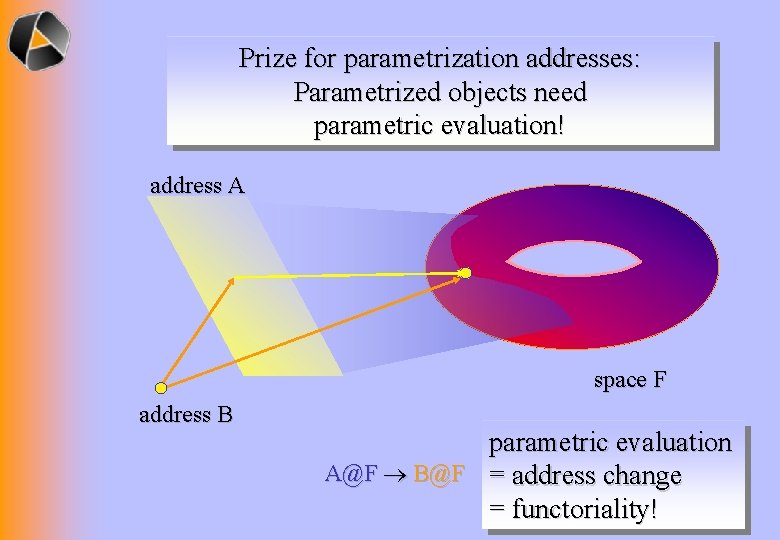
Prize for parametrization addresses: Parametrized objects need parametric evaluation! address A space F address B parametric evaluation A@F B@F = address change = functoriality!

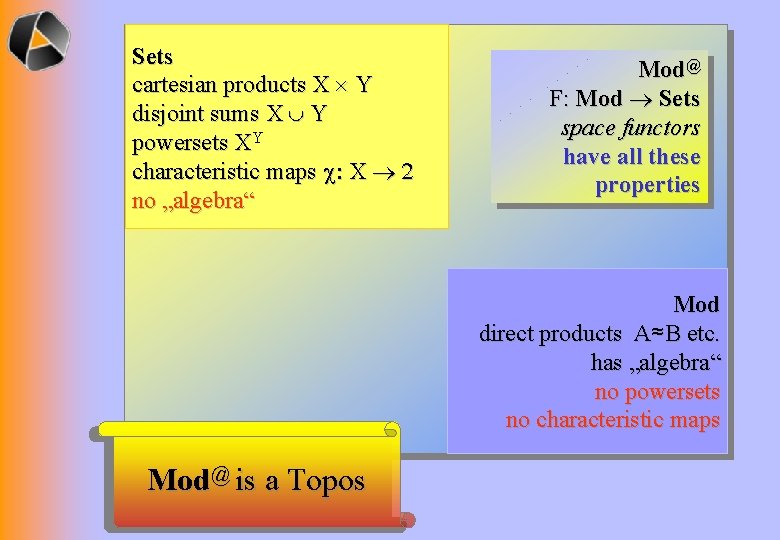
Sets cartesian products X Y disjoint sums X È Y powersets XY characteristic maps c: X 2 no „algebra“ Mod@ F: Mod Sets space functors have all these properties Mod direct products A≈B etc. has „algebra“ no powersets no characteristic maps Mod@ is a Topos

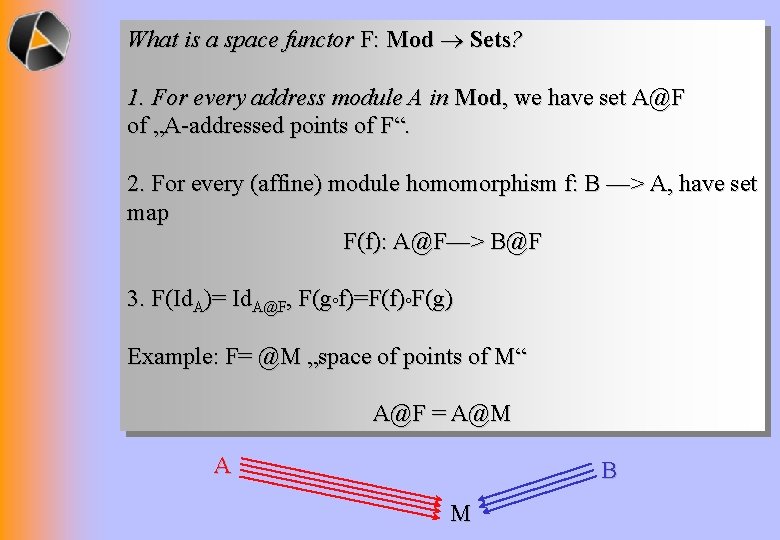
What is a space functor F: Mod Sets? 1. For every address module A in Mod, we have set A@F of „A-addressed points of F“. 2. For every (affine) module homomorphism f: B —> A, have set map F(f): A@F—> B@F 3. F(Id. A)= Id. A@F, F(g f)=F(f) F(g) Example: F= @M „space of points of M“ A@F = A@M A B M

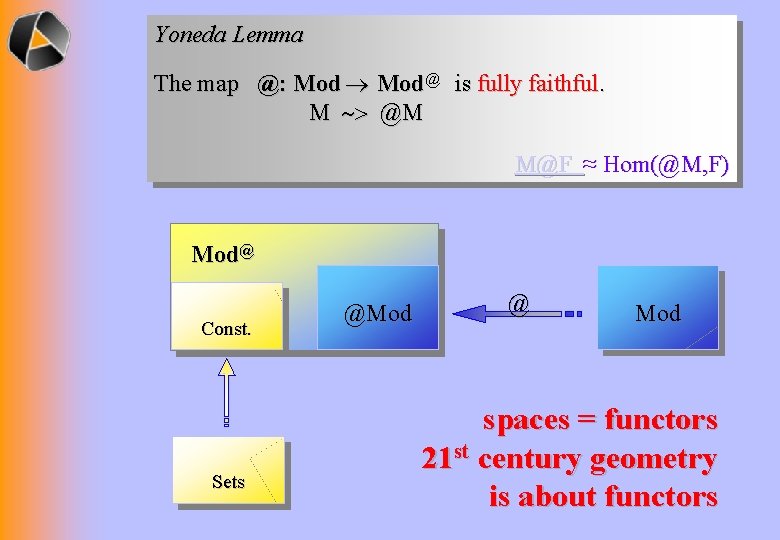
Yoneda Lemma The map @: Mod@ is fully faithful. M ~> @M M@F ≈ Hom(@M, F) Mod@ Const. Sets @Mod @ Mod spaces = functors 21 st century geometry is about functors

The Topos of Music is mainly concerned with powerset type categories and their classification: „Local and global compositions“

disjunction disjoint sum colimit conjunction cartesian product limit Makro. Note Satellites Anchor. Note Makro. Note Resr Onset – Note Duration – Onset – Pitch Ÿ Loudness STRG selection set powerset Duration – representation algebraic space group, module, etc.

Henry Klumpenhouwer: Deep Structure in K-net Analysis with Special Reference to Webern‘s Opus 16, 4 Atlas for global composition made of 8 local compositions I 1 , I 2 , I 3 , I 4 , I 5 , I 6 , I 7 , I 8 I 1 I 2 I 3 I 4 I 5 I 6 I 7 1 -dimensional nerve of global composition J 1 , J 2 , J 3 , J 4 , J 5 , J 6 , J 7 , J 8 Jk 0@Pi. Mod 12 J 1 J 2 J 3 J 8 J 4 J 7 J 5 J 6 class 19 class 22 class 28 class 31 I 8

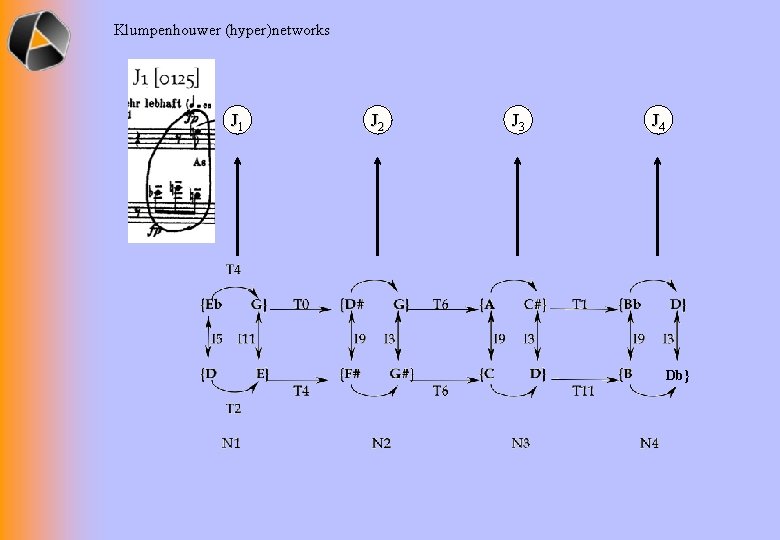
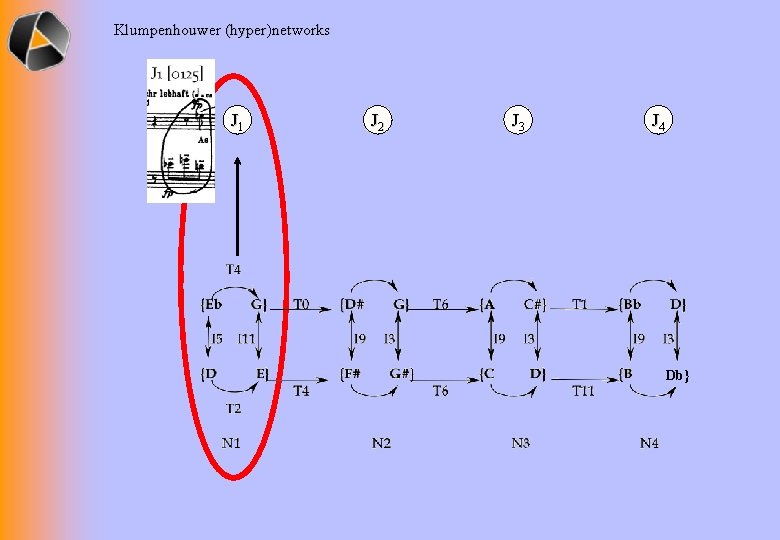
Klumpenhouwer (hyper)networks J 1 J 2 J 3 J 4 Db}

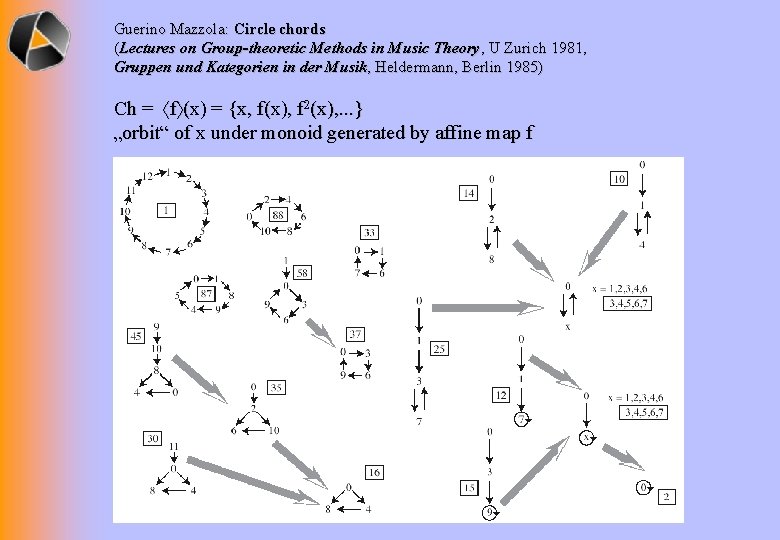
Guerino Mazzola: Circle chords (Lectures on Group-theoretic Methods in Music Theory, U Zurich 1981, Gruppen und Kategorien in der Musik, Heldermann, Berlin 1985) Ch = f (x) = {x, f(x), f 2(x), . . . } „orbit“ of x under monoid generated by affine map f

Klumpenhouwer (hyper)networks J 1 J 2 J 3 J 4 Db}

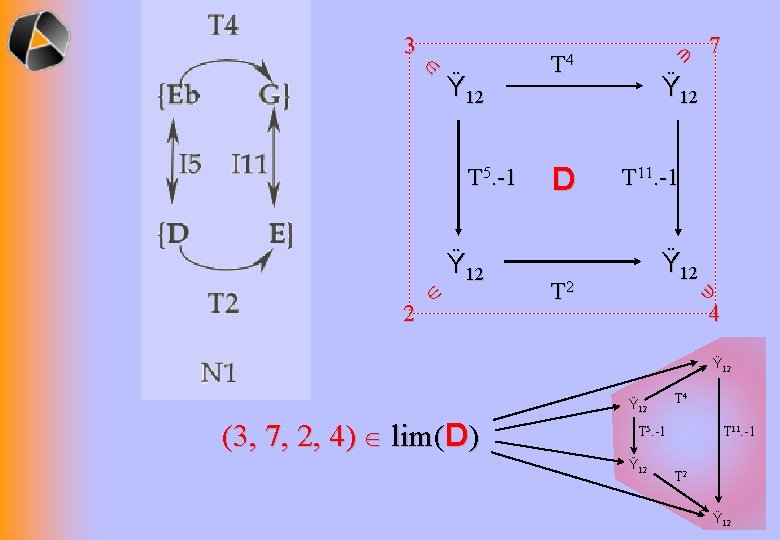
T 5. -1 2 Ÿ 12 T 4 D 7 Ÿ 12 T 11. -1 Ÿ 12 T 2 Ÿ 12 3 4 Ÿ 12 (3, 7, 2, 4) lim(D) T 4 T 5. -1 Ÿ 12 T 11. -1 T 2 Ÿ 12

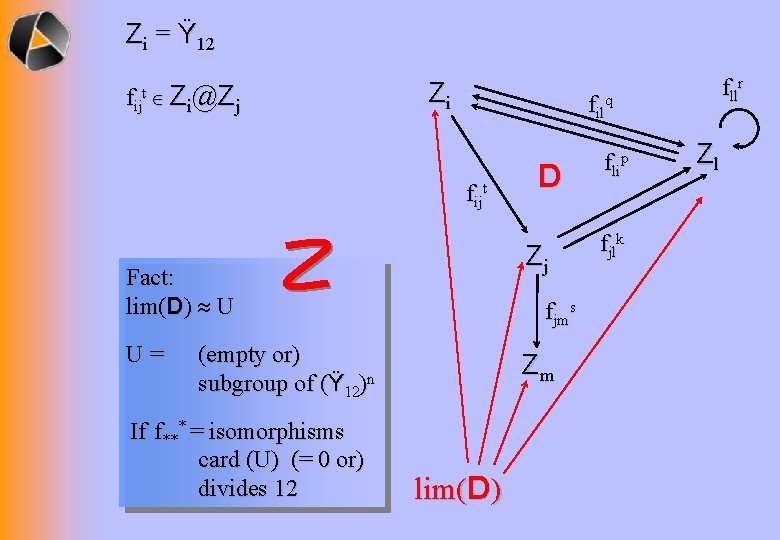
Zi = Ÿ 12 fijt Z i@ Z j Zi filq fijt fjms (empty or) subgroup of (Ÿ 12)n If f*** = isomorphisms card (U) (= 0 or) divides 12 D Zj Fact: lim(D) U U= fllr Zm lim(D) flip fjlk Zl

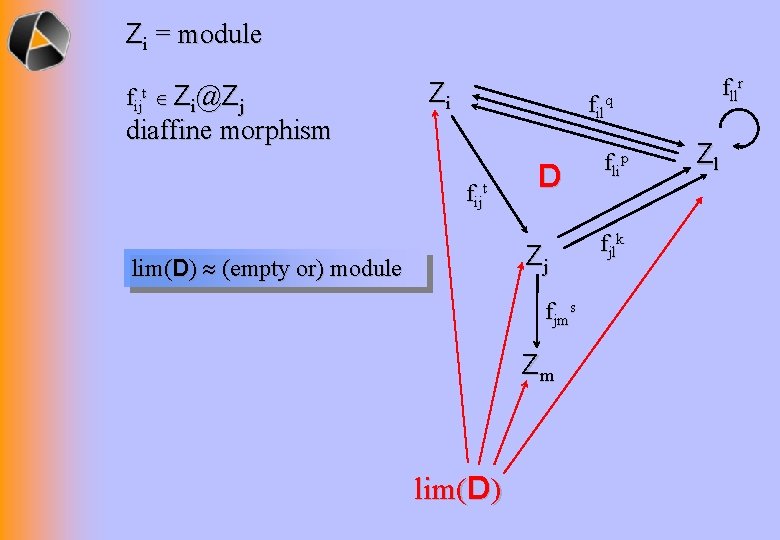
Zi = module fijt Z i@ Z j Zi fllr filq diaffine morphism fijt D Zj lim(D) (empty or) module fjms Zm lim(D) flip fjlk Zl

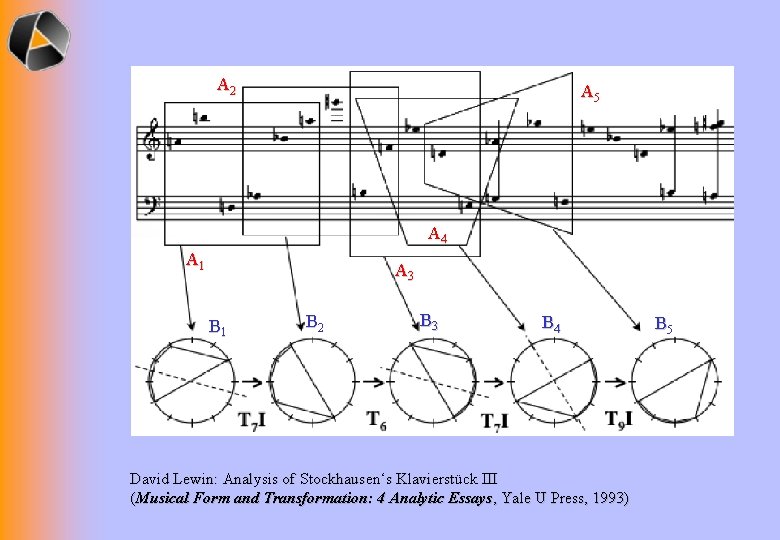
A 2 A 5 A 4 A 1 A 3 B 1 B 2 B 3 B 4 David Lewin: Analysis of Stockhausen‘s Klavierstück III (Musical Form and Transformation: 4 Analytic Essays, Yale U Press, 1993) B 5

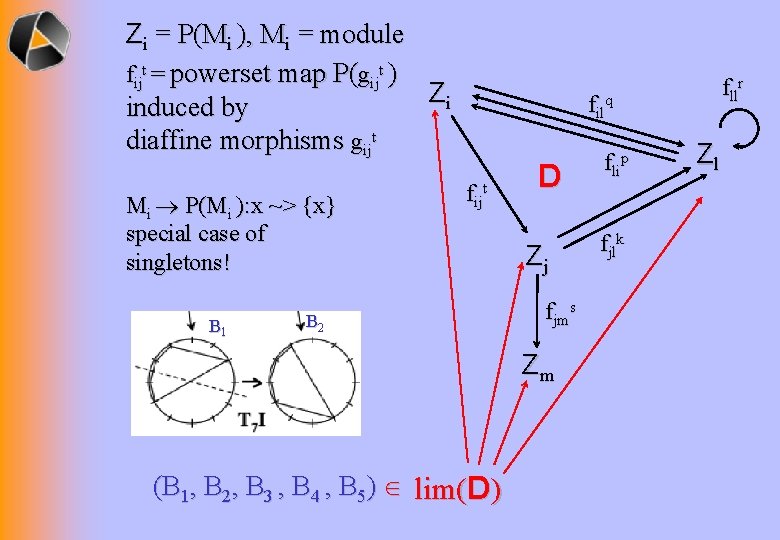
Zi = P(Mi ), Mi = module fijt = powerset map P(gijt ) Zi induced by diaffine morphisms gijt Mi P(Mi ): x ~> {x} special case of singletons! B 1 fllr filq fijt B 2 D Zj fjms Zm (B 1, B 2, B 3 , B 4 , B 5) lim(D) flip fjlk Zl

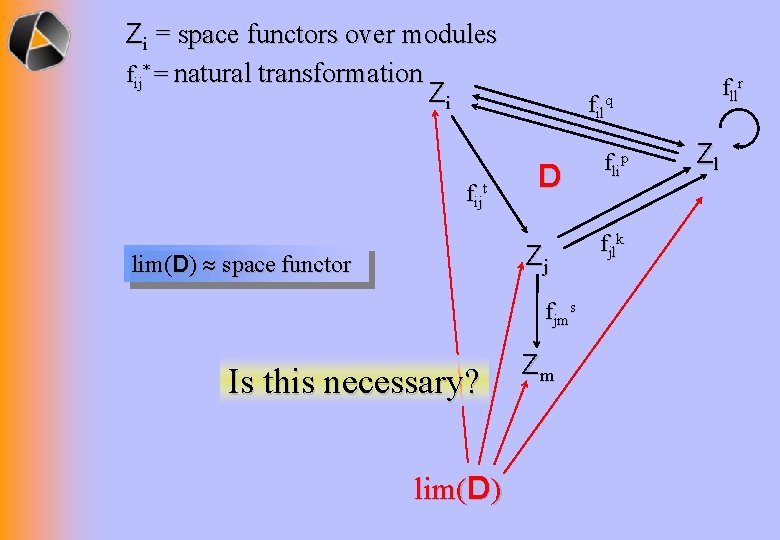
Zi = space functors over modules fij* = natural transformation Zi fijt filq D Zj lim(D) space functor fjms Is this necessary? lim(D) fllr Zm flip fjlk Zl

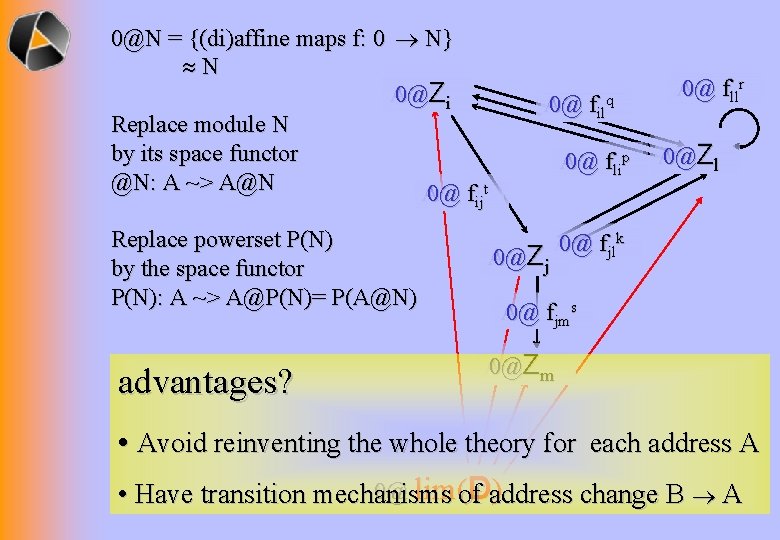
0@N = {(di)affine maps f: 0 N} N 0@Zi A@ Replace module N by its space functor @N: A ~> A@N 0@ f tt A@ 0@ fililqq A@ 0@ fflilipp A@ 0@ fllr A@ 0@Zl A@ ijij Replace powerset P(N) by the space functor P(N): A ~> A@P(N)= P(A@N) advantages? 0@Zjj A@ 0@ fjlk A@ ss 0@ fjm A@ jm 0@Zm A@ • Avoid reinventing the whole theory for each address A 0@ lim(of Daddress ) A@ • Have transition mechanisms change B A

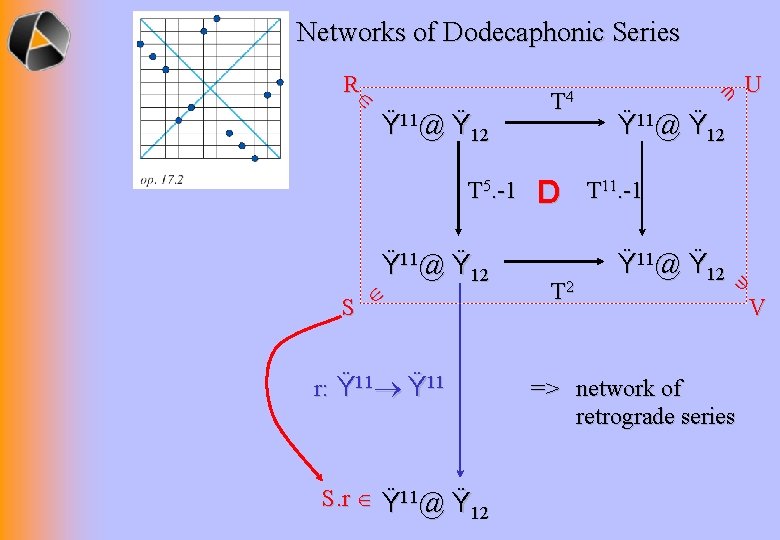
Networks of Dodecaphonic Series T 5. -1 Ÿ 11@ Ÿ 12 S r: Ÿ 11 S. r Ÿ 11@ Ÿ 12 D T 2 U Ÿ 11@ Ÿ 12 T 11. -1 Ÿ 11@ Ÿ 12 => network of retrograde series Ÿ 11@ Ÿ 12 T 4 R V

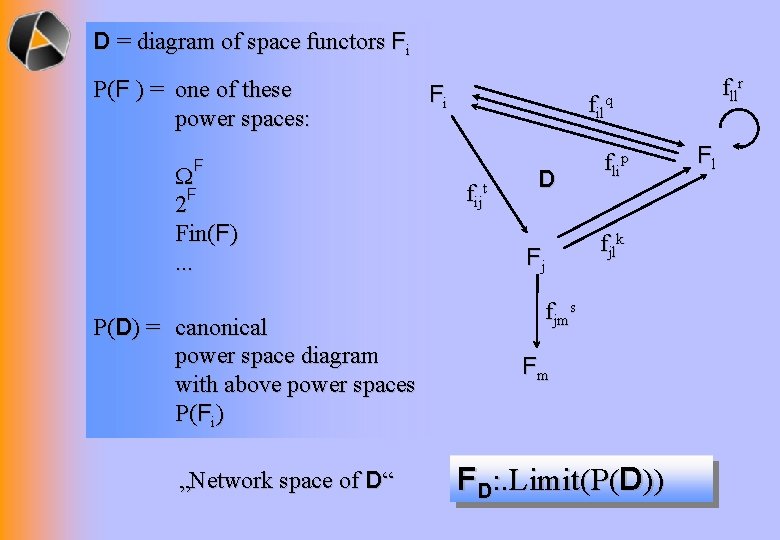
D = diagram of space functors Fi P(F ) = one of these power spaces: Fi filq F F 2 Fin(F). . . P(D) = canonical power space diagram with above power spaces P(Fi) „Network space of D“ fllr fijt D Fj flip fjlk fjms Fm FD: . Limit(P(D)) Fl

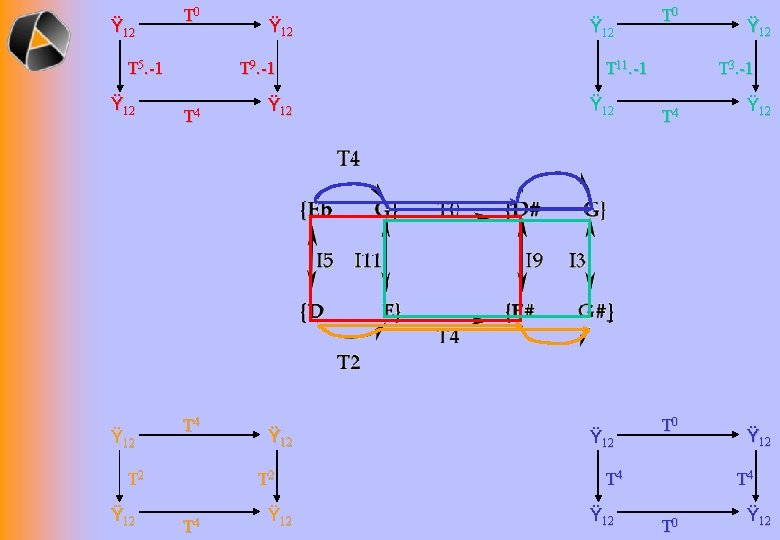
Ÿ 12 T 0 T 5. -1 Ÿ 12 T 9. -1 T 4 T 2 Ÿ 12 T 4 Ÿ 12 T 0 T 11. -1 Ÿ 12 T 3. -1 T 4 T 0 T 4 Ÿ 12 T 4 T 0 Ÿ 12

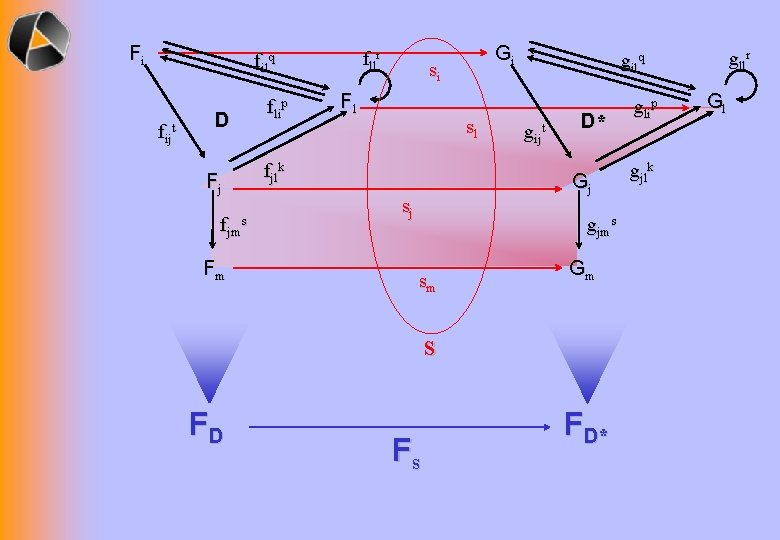
Fi fllr filq fijt D Fj fjms Fm flip Gi si Fl sl fjlk gijt D* Gj sj gjms sm Gm s FD Fs gllr gilq F D* glip gjlk Gl

Summarizing recursive procedure: 1. Given are -> Category C of spaces -> Diagram scheme D. 2. Consider category Dia(D, C ) of diagrams D over D with values in C, plus natural transformations S: D D*. 3. Define category C (1) =D PC of limits FD of power diagrams P(D) of one of the power types P = D, 2 D, Fin(D), . . . , together with morphisms FS : FD FD*. 4. Restart the procedure from 1. with the new category C (1) and a new diagram scheme D(1), defining the category C (2) =D(1) P (1) C (1), and so on. . . Problem: ¿Is there an operation P on diagram schemes with (D(1) PD) PC =D(1) P(D PC )

global compositions charts atlases

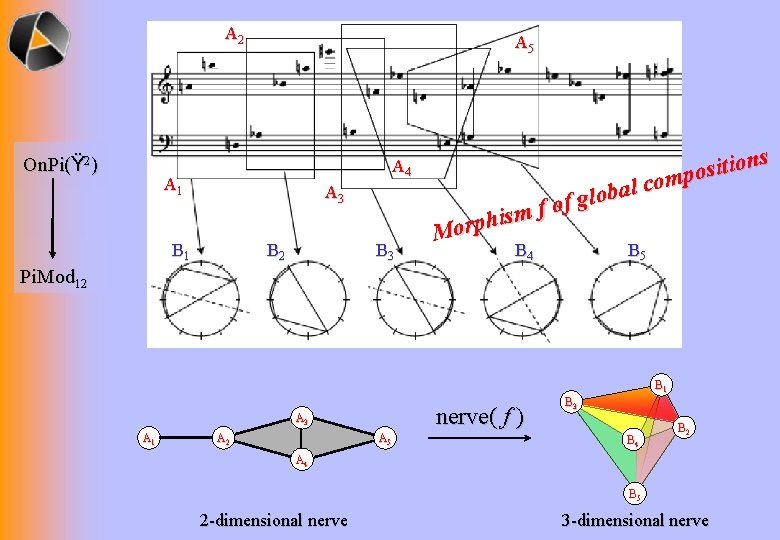
A 2 On. Pi(Ÿ 2) A 5 A 4 A 1 A 3 B 1 B 2 B 3 hism p r o M al b o l g f of B 4 s n o i t i s compo B 5 Pi. Mod 12 B 1 nerve( f ) A 3 A 1 A 2 A 5 B 3 B 4 B 2 A 4 B 5 2 -dimensional nerve 3 -dimensional nerve

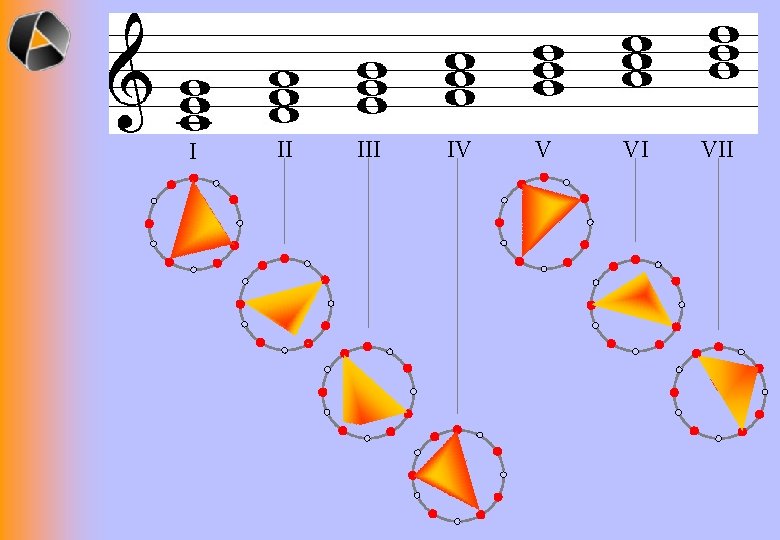
I II IV V VI VII

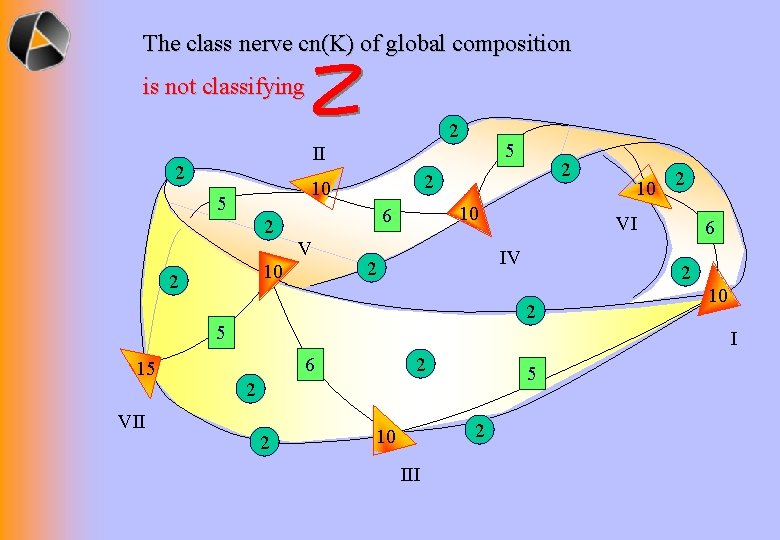
The class nerve cn(K) of global composition is not classifying 2 5 II 2 10 5 10 2 10 6 2 V VII 10 2 VI IV 2 6 2 2 5 15 2 2 10 I 2 6 5 2 2 2 10 III

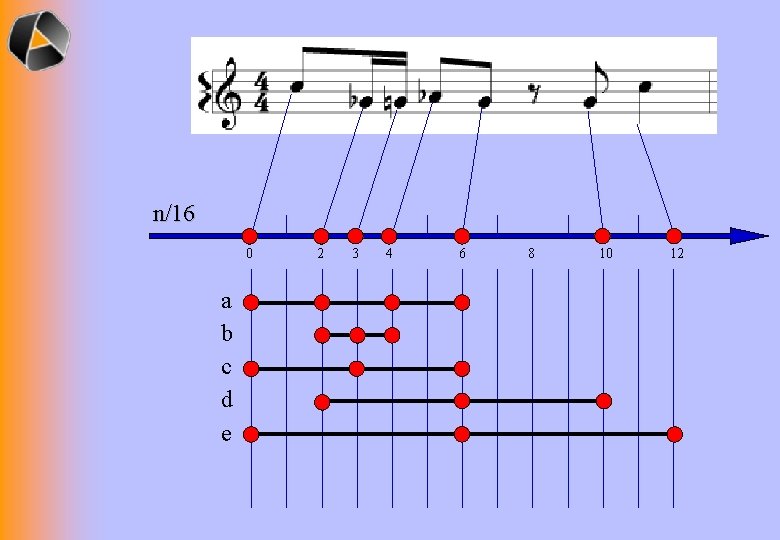
n/16 0 a b c d e 2 3 4 6 8 10 12

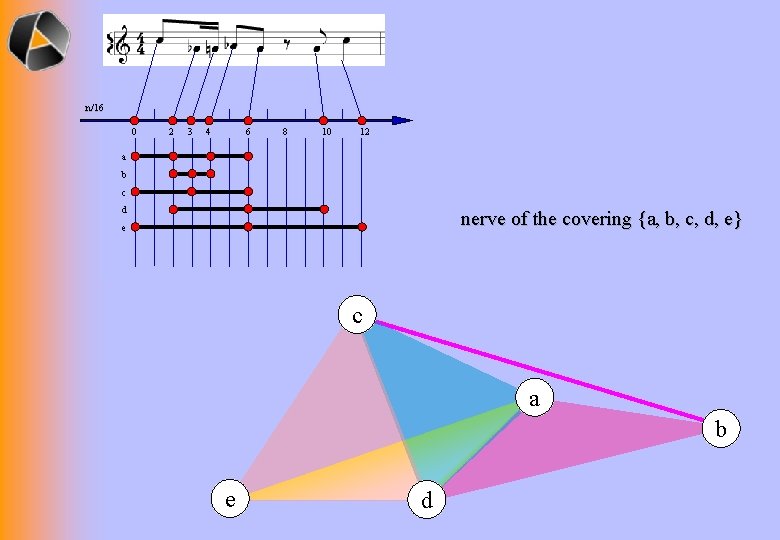
n/16 0 2 3 4 6 8 10 12 a b c d nerve of the covering {a, b, c, d, e} e c a b e d

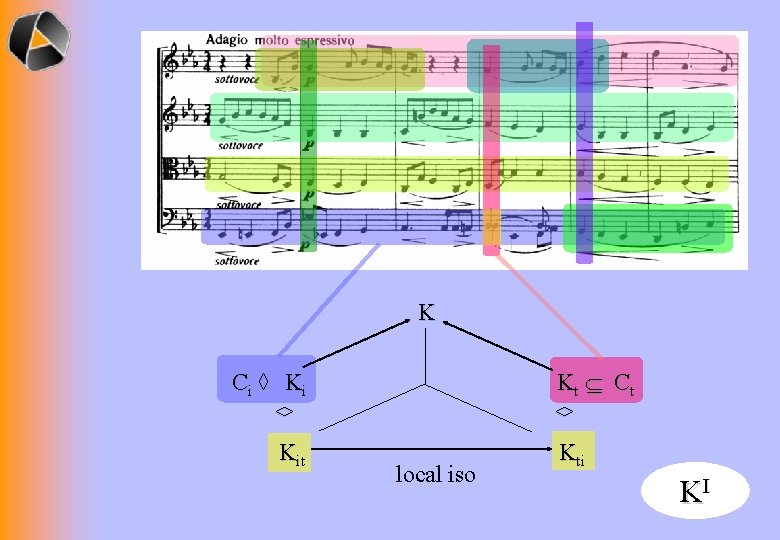
K Kt Í C t C i ◊ Ki ◊ ◊ Kit local iso Kti KI

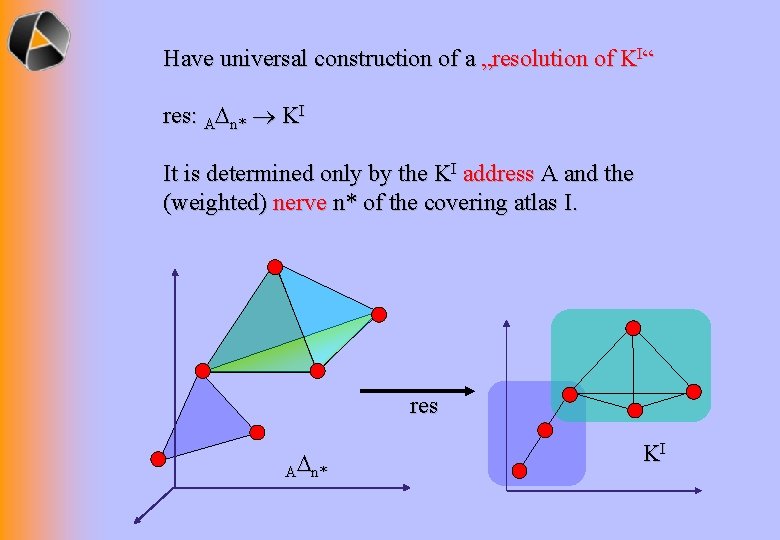
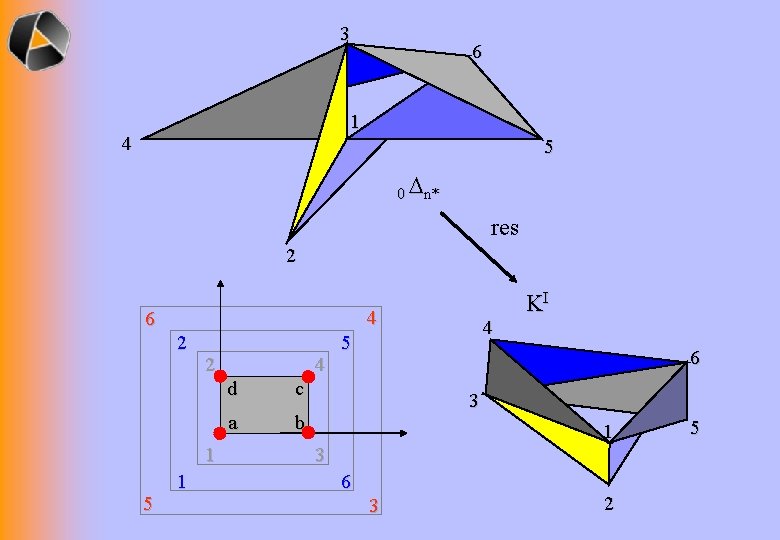
Have universal construction of a „resolution of KI“ res: A n* KI It is determined only by the KI address A and the (weighted) nerve n* of the covering atlas I. res A n* KI

3 6 1 4 5 0 n* res 2 4 6 2 2 1 5 1 4 d c a b 4 5 KI 6 3 1 3 6 3 2 5

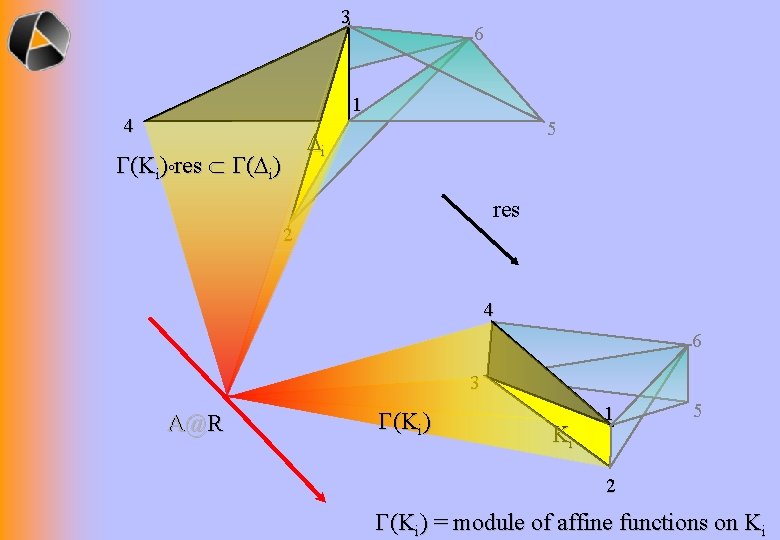
3 6 1 4 5 i (Ki) res ( i) res 2 4 6 3 A@R (K i ) Ki 1 5 2 (Ki) = module of affine functions on Ki

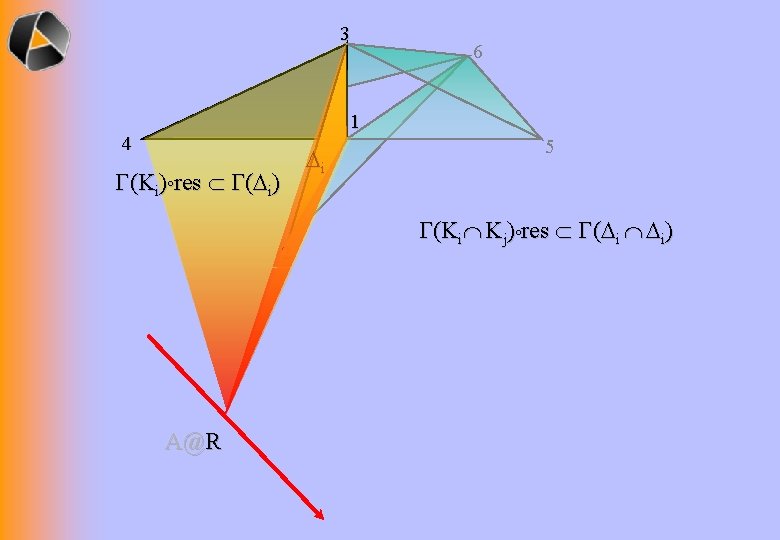
3 6 1 4 (Ki) res ( i) 2 A@R i 5 (Ki Kj) res ( i i)

n* ≈ n*(KI) = nerve of KI , n* A n*( ) —» A n*( ) homomorphism of R-modules KI( ) res » A n*( ) » KI( ) res*n (KI) n (A n*)

D(n*) = diagram of function spaces F F f ( / ) P(F ) = Sub. Mod(F ) P(D (n*)) = canonical power space diagram with the above power spaces P(F ) D(n*) f ( / ) F „Network space of D(n*) “ FD (n*) : . Limit(P(D(n*) )) KI-Functions: A@FD (n*) (res*n (KI)) F

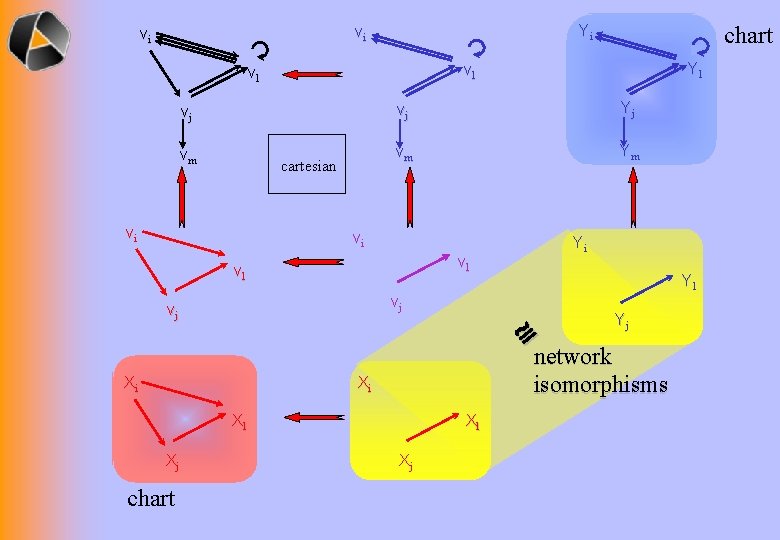
Yi vi vi Yl vl vl vj vj Yj vm vm Ym cartesian vi vi vj vj Xi Yl Yj network isomorphisms Xi Xl chart Yi vl vl Xj chart Xl Xj

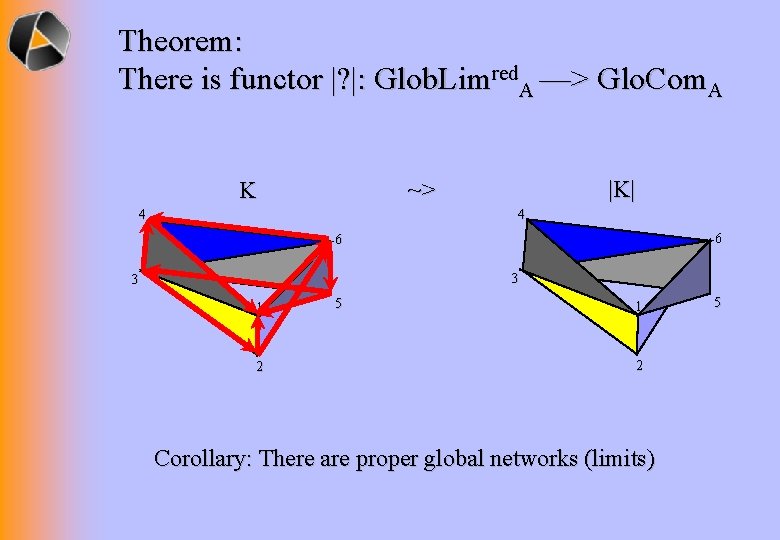
Theorem: There is functor |? |: Glob. Limred. A —> Glo. Com. A ~> K |K| 4 4 6 6 3 3 1 2 5 1 2 Corollary: There are proper global networks (limits) 5

Structures Processes ! ? ? Gestures

Remark on automorphism groups on Ÿ 12 Aut(Ÿ 12) = TŸ 12 | Ÿ 12* T/I group = subgroup of Aut(Ÿ 12) T/I group = TŸ 12 | (± 1) Ÿ 12 | Ÿ 2 Int: Aut(Ÿ 12) Aut(T/I group) Ÿ 12 | Ÿ 12* Ker(Int) = <T 6 > Ÿ 2 <j, n>(Tu) = Tnu, n Ÿ 12* ={1, 5, 7, 11} <j, n>(-1) = Tj(-1) Int(Ts(n)) = <2 s, n> Im(Int) 2Ÿ 12 | Ÿ 12*

Remark on isographies on Ÿ 12 An isography between two diagrams D, D* : D T/I-group over the same diagram scheme D with values in category T/I-group with • the single object Ÿ 12 • morphisms = T/I-group isomorphisms is a group automorphism f (= a functorial automorphism) f: T/I-group D D* T/I-group f ~ such that D* = f D D T/I-group

Unfortunately, an isography f between two diagrams D, D* : D T/I-group does not tell anything about the underlying limits! Example: D Ÿ 12 lim(D) = Ø T 2 q+1(-1) x = 2 q+1 -x <2 q+1, 1> D* lim(D *) Ø Ÿ 12 T 2(2 q+1)(-1) x = 2(2 q+1) -x However, an isography with <2 s, n>, stemming from conjugation, preserves limits, i. e. , it is a natural transformation!