Just and Welltempered Modulation Theory Guerino Mazzola U

Just and Well-tempered Modulation Theory Guerino Mazzola U & ETH Zürich Internet Institute for Music Science guerino@mazzola. ch www. encyclospace. org

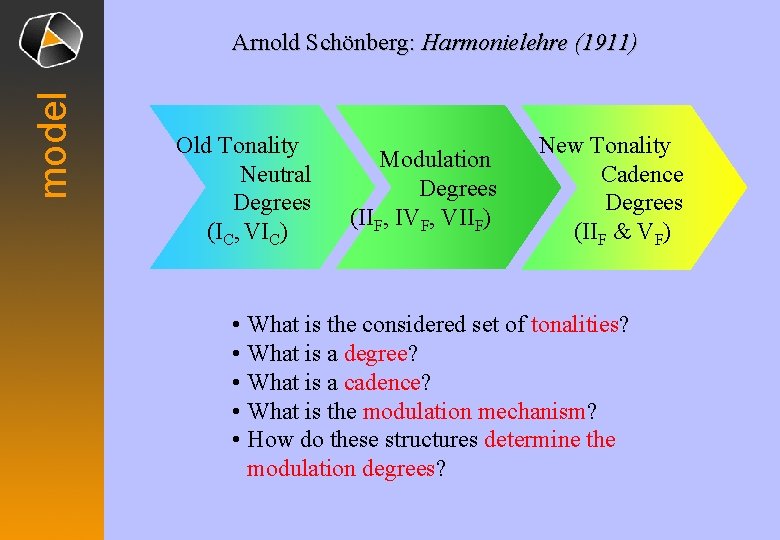
model Arnold Schönberg: Harmonielehre (1911) Old Tonality Neutral Degrees (IC, VIC) Modulation Degrees (IIF, IVF, VIIF) New Tonality Cadence Degrees (IIF & VF) • What is the considered set of tonalities? • What is a degree? • What is a cadence? • What is the modulation mechanism? • How do these structures determine the modulation degrees?

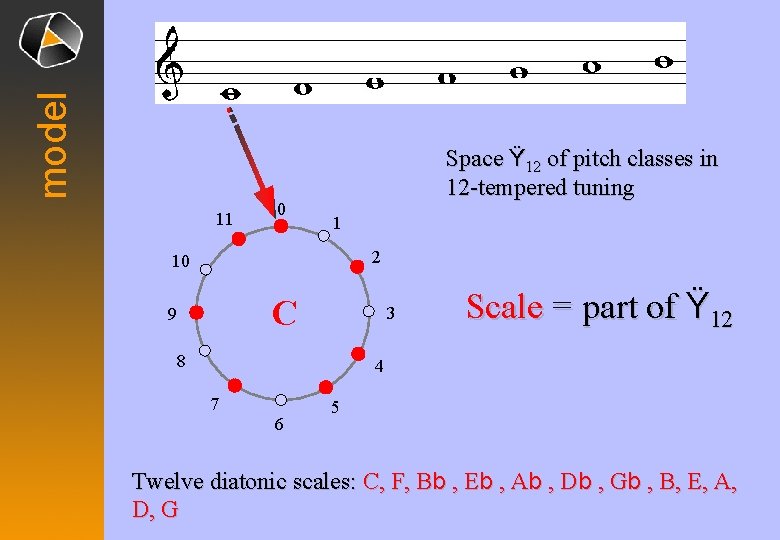
model 11 0 Space Ÿ 12 of pitch classes in 12 -tempered tuning 1 2 10 C 9 3 8 Scale = part of Ÿ 12 4 7 6 5 Twelve diatonic scales: C, F, Bb , Eb , Ab , Db , Gb , B, E, A, D, G

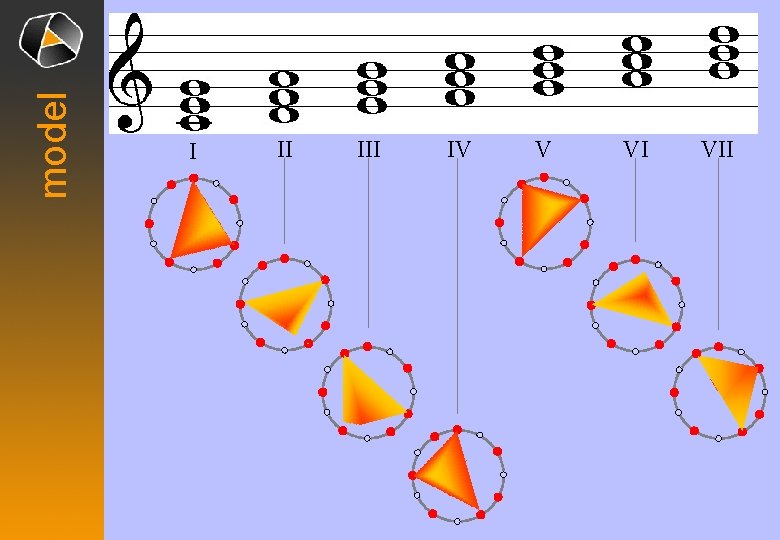
model I II IV V VI VII

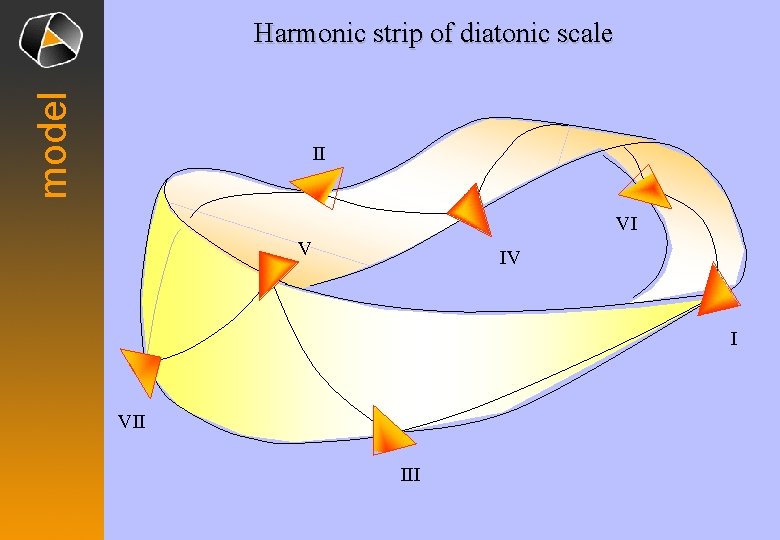
model Harmonic strip of diatonic scale II VI V IV I VII III

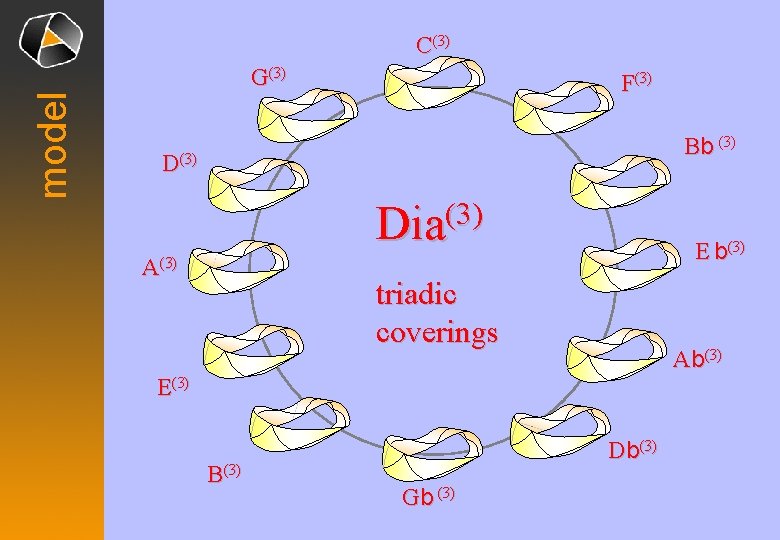
model C(3) G(3) F(3) Bb (3) Dia(3) A(3) E b(3) triadic coverings Ab(3) E(3) B(3) Db(3) Gb (3)

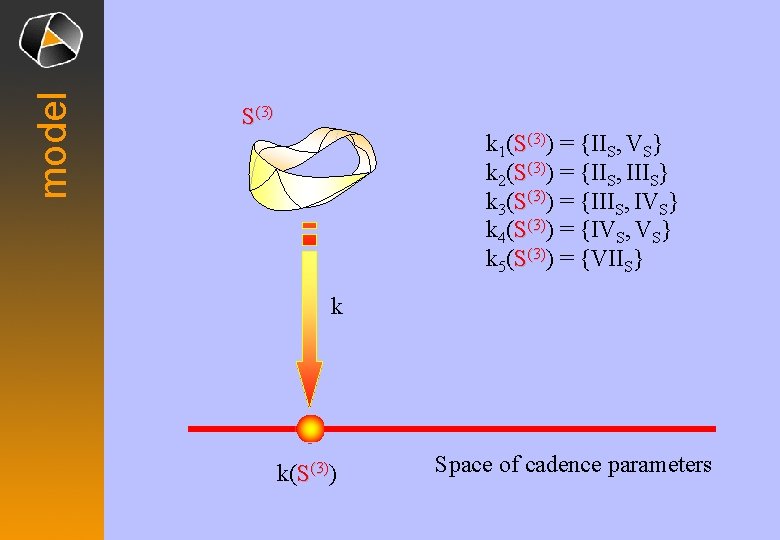
model S(3) k 1(S(3)) = {IIS, VS} k 2(S(3)) = {IIS, IIIS} k 3(S(3)) = {IIIS, IVS} k 4(S(3)) = {IVS, VS} k 5(S(3)) = {VIIS} k k(S(3)) Space of cadence parameters

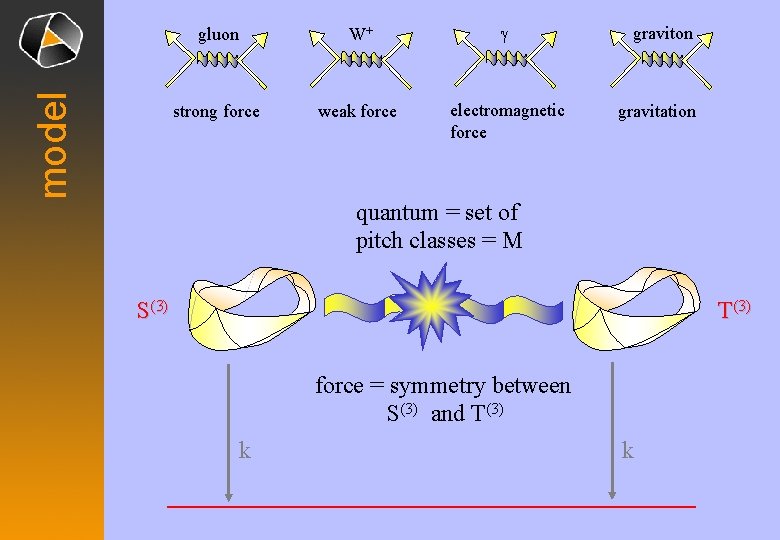
model gluon W+ g strong force weak force electromagnetic force graviton gravitation quantum = set of pitch classes = M S(3) T(3) force = symmetry between S(3) and T(3) k k

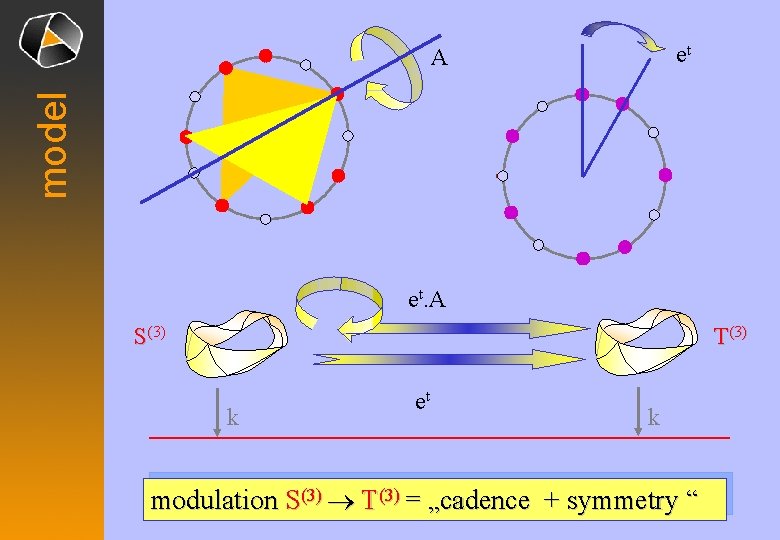
et model A et. A S(3) T(3) k et k modulation S(3) ® T(3) = „cadence + symmetry “

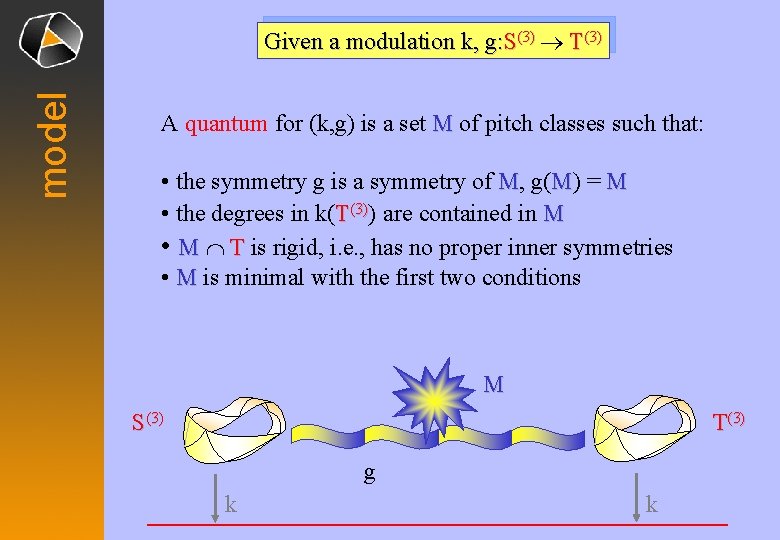
model Given a modulation k, g: S(3) ® T(3) A quantum for (k, g) is a set M of pitch classes such that: • the symmetry g is a symmetry of M, g(M) = M • the degrees in k(T(3)) are contained in M • M Ç T is rigid, i. e. , has no proper inner symmetries • M is minimal with the first two conditions M S(3) T(3) g k k

model Modulation Theorem for 12 -tempered Case For any two (different) tonalities S(3), T(3) there is • a modulation (k, g) and • a quantum M for (k, g) Further: • M is the union of the degrees in S(3), T(3) contained in M, and thereby defines the triadic covering M(3) of M • the common degrees of T(3) and M(3) are called the modulation degrees of (k, g) • the modulation (k, g) is uniquely determined by the modulation degrees.

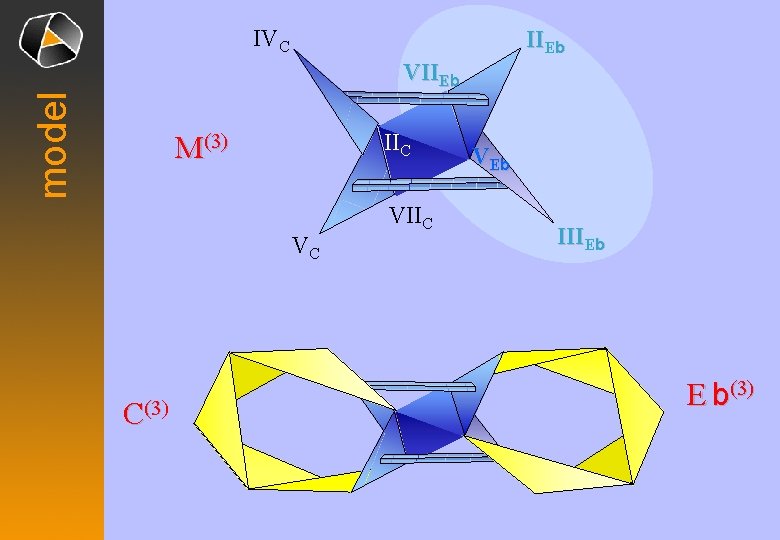
IVC IIEb model VIIEb IIC M(3) VC C(3) VIIC VE b IIIEb E b(3)

Ludwig van Beethoven: op. 130/Cavatina/# 41 experiments Inversion e b : E b(3) ® B(3) 4: 00 mi-b->si

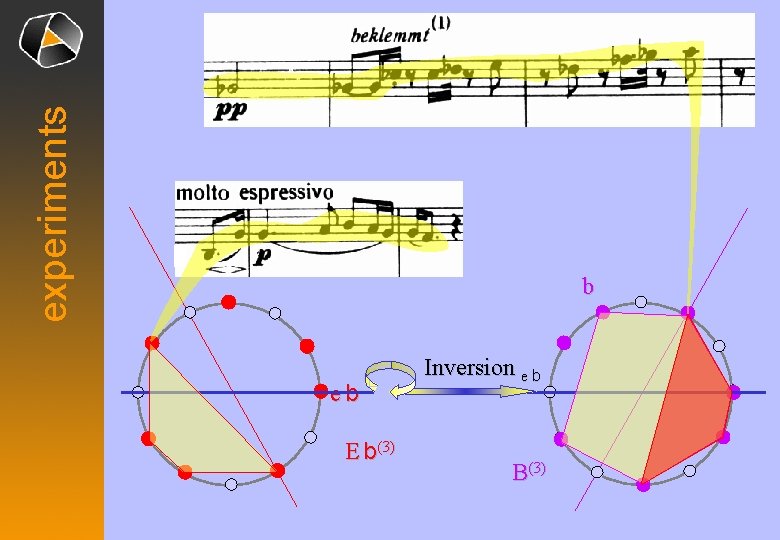
experiments b eb E b(3) Inversion e b B(3)

Ludwig van Beethoven: op. 106/Allegro/#124 -127 experiments Inversiondb : G(3) ® E b(3) 4: 50 sol->mi b #124 - 125 #126 - 127 g db g

Ludwig van Beethoven: op. 106/Allegro/#188 -197 experiments Catastrophe : E b(3) ® D(3)~ b(3) 6: 00 mi b->re= Si min.

experiments Theses of Erwin Ratz (1973) and Jürgen Uhde (1974) Ratz: The „sphere“ of tonalities of op. 106 is polarized into a „world“ centered around B-flat major, the principal tonality of this sonata, and a „antiworld“ around B minor. Uhde: When we change Ratz‘ „worlds“, an event happening twice in the Allegro movement, the modulation processes become dramatic. They are completely different from the other modulations, Uhde calls them „catastrophes“. B-flat major B minor

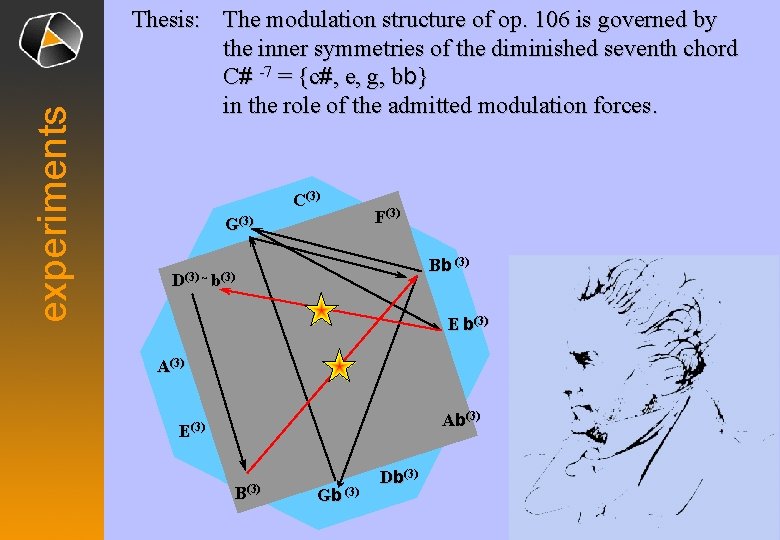
experiments Thesis: The modulation structure of op. 106 is governed by the inner symmetries of the diminished seventh chord C# -7 = {c#, e, g, bb} in the role of the admitted modulation forces. C(3) G(3) F(3) Bb (3) D(3) ~ b(3) E b(3) Ab(3) E(3) B(3) Gb (3) Db(3)

generalization Modulation Theorem for 12 -tempered 7 -tone Scales S and triadic coverings S(3) (Muzzulini) q-modulation = quantized modulation (1) S(3) is rigid. • For every such scale, there is at least one q-modulation. • The maximum of 226 q-modulations is achieved by the harmonic scale #54. 1, the minimum of 53 q-modulations occurs for scale #41. 1. (2) S(3) is not rigid. • For scale #52 and #55, there are q-modulations except for t = 1, 11; for #38 and #62, there are q-modulations except for t = 5, 7. All 6 other types have at least one quantized modulation. • The maximum of 114 q-modulations occurs for the melodic minor scale #47. 1. Among the scales with q-modulations for all t, the diatonic major scale #38. 1 has a minimum of 26.

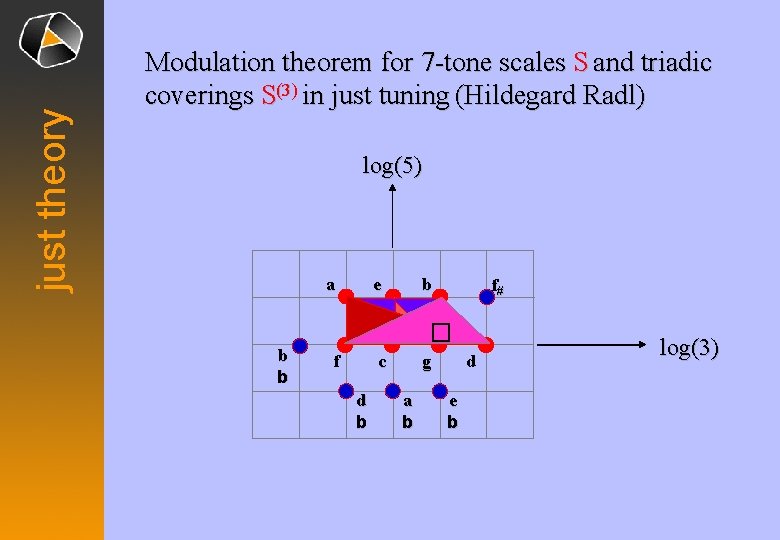
just theory Modulation theorem for 7 -tone scales S and triadic coverings S(3) in just tuning (Hildegard Radl) log(5) a e b f# � b b f c d b d g a b e b log(3)

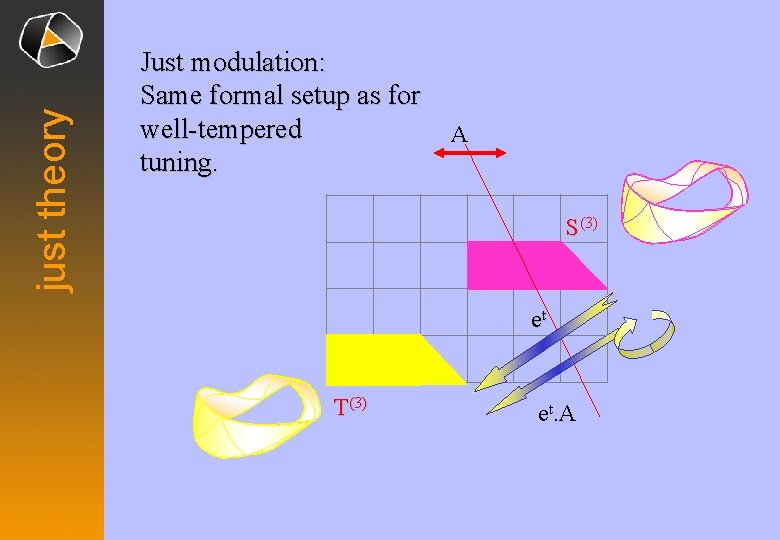
just theory Just modulation: Same formal setup as for well-tempered tuning. A S(3) et T(3) et. A

just theory Lemma: If the seven-element scale S is generating, a non-trivial automorphism A of S(3) is of order 2. Proof: The nerve automorphism Nerve(A) on Nerve(S(3)) preserves the boundary circle of the Möbius strip and hence is in the dihedral group of the 7 -angle. By Minkowsky‘s theorem, the composed group homomorphism <A> ® GL 2(Ÿ) ® GL 2(Ÿ 3) is injective. Since #GL 2(Ÿ 3) = 48, the order is 2. Lemma: Let M = et. A: S(3) ® T(3) be a modulator, with A = ea. R. For any x Î Ÿ 2, the <M>-orbit is <M>(x) = e Ÿ(1+R)t. x È e Ÿ(1+R)t. M(x)

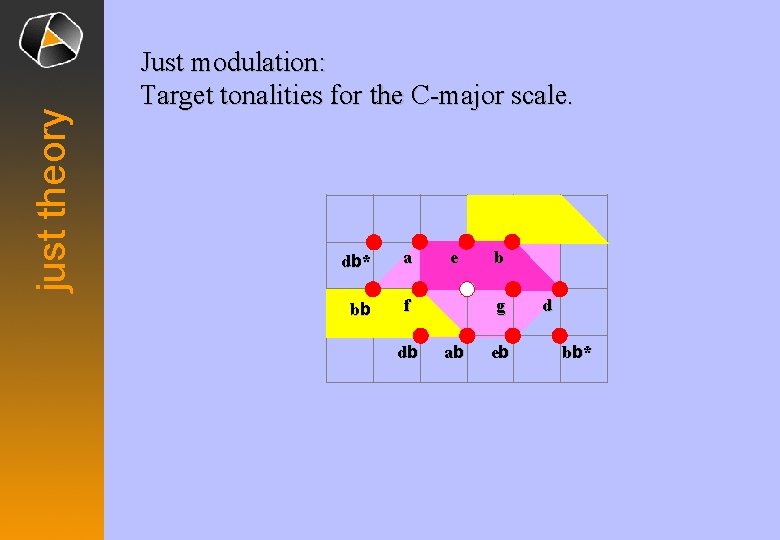
just theory Just modulation: Target tonalities for the C-major scale. db * a bb f db e b g ab eb d bb *

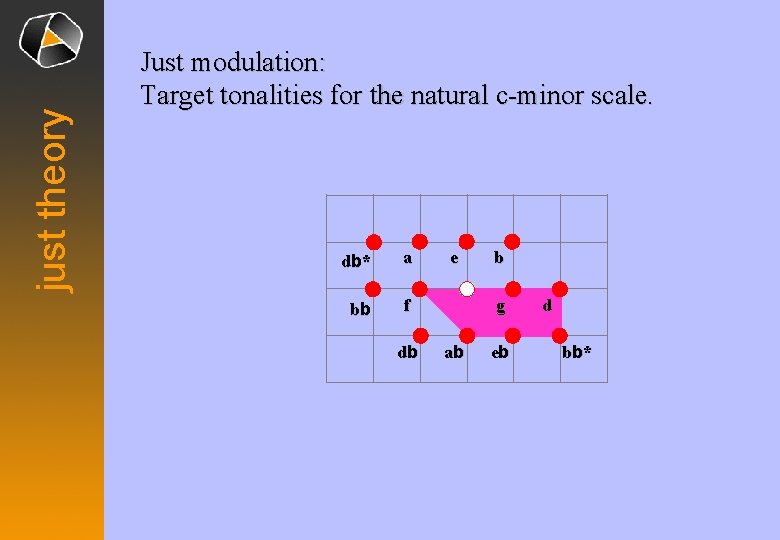
just theory Just modulation: Target tonalities for the natural c-minor scale. db * a bb f db e b g ab eb d bb *

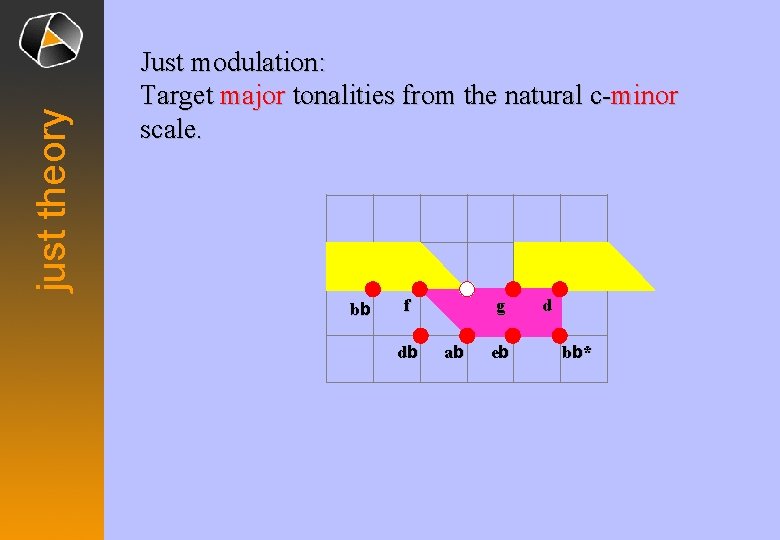
just theory Just modulation: Target major tonalities from the natural c-minor scale. bb f db g ab eb d bb *

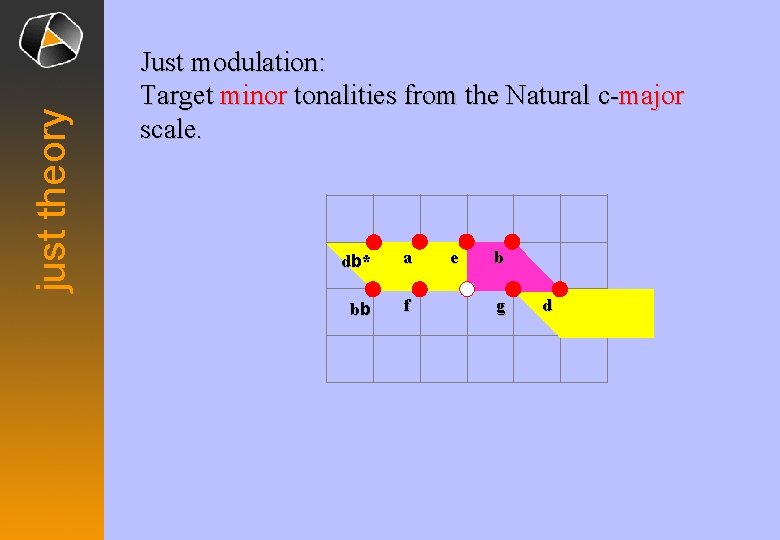
just theory Just modulation: Target minor tonalities from the Natural c-major scale. db * a bb f e b g d

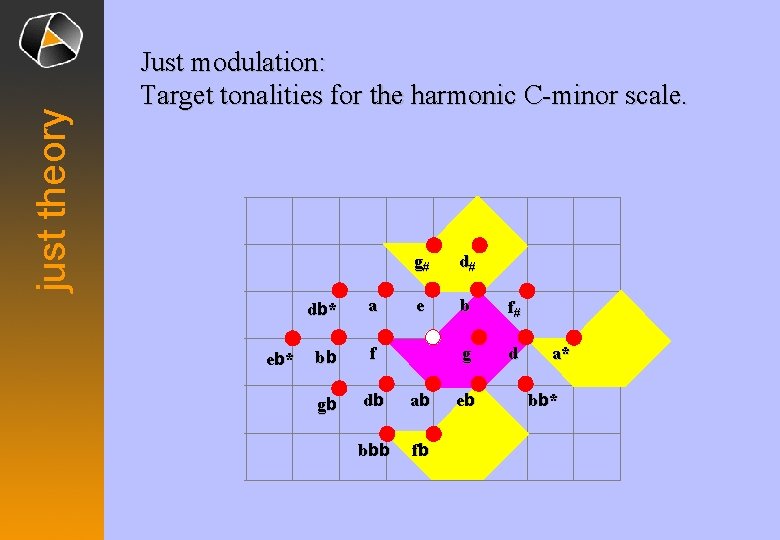
just theory Just modulation: Target tonalities for the harmonic C-minor scale. eb* g# d# e b f# g d db * a bb f gb db ab bbb fb eb a* bb *

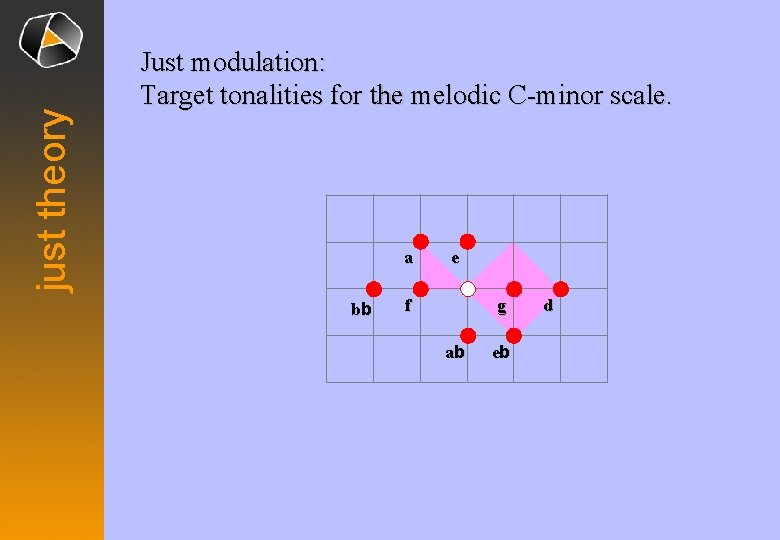
just theory Just modulation: Target tonalities for the melodic C-minor scale. a bb e f g ab eb d

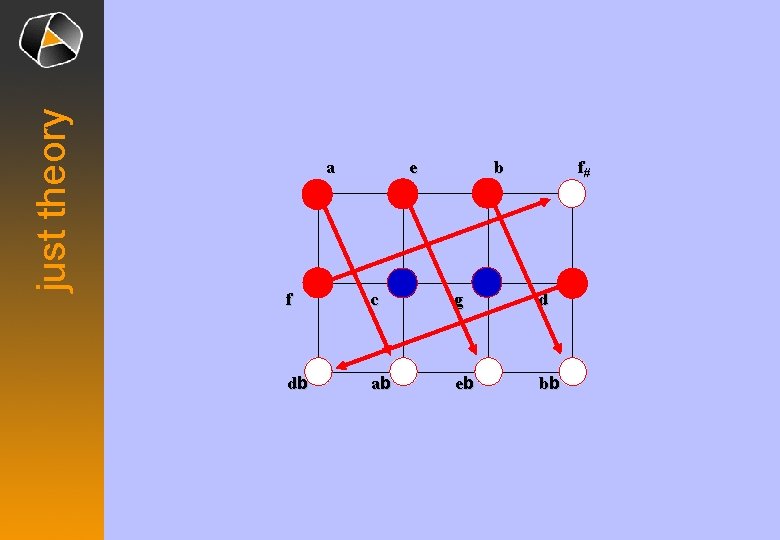
just theory a e f# b f c g d db ab eb bb

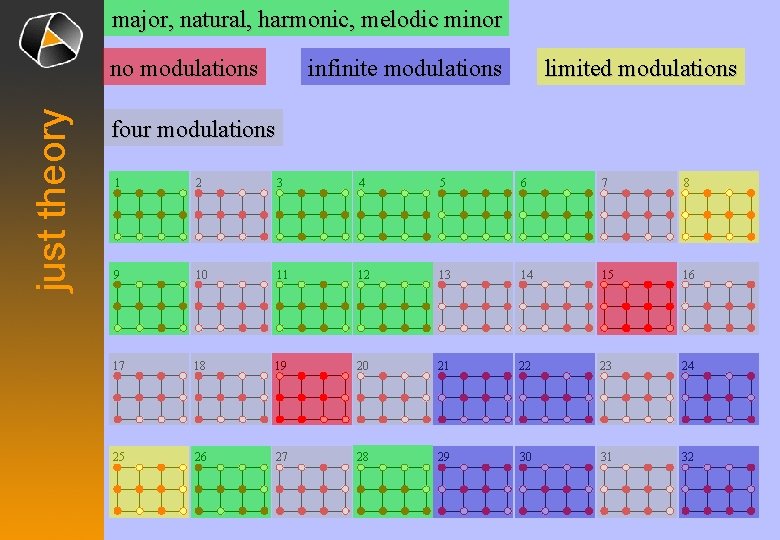
major, natural, harmonic, melodic minor just theory no modulations infinite modulations limited modulations four modulations 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

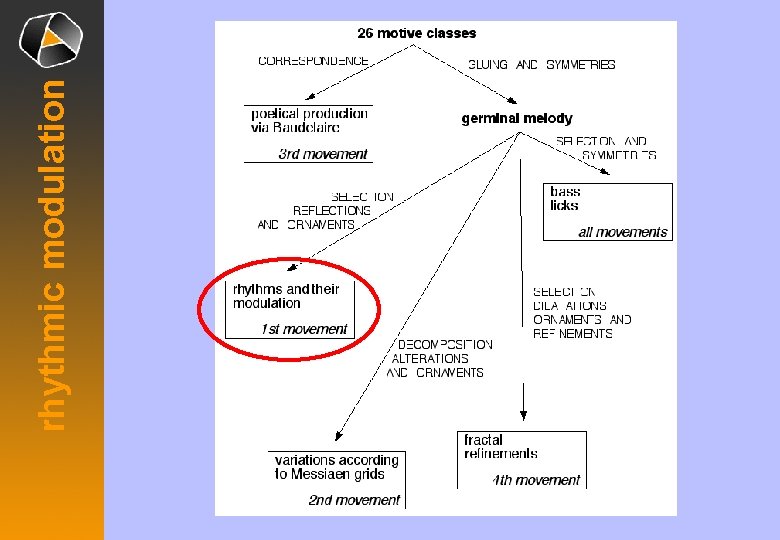
rhythmic modulation

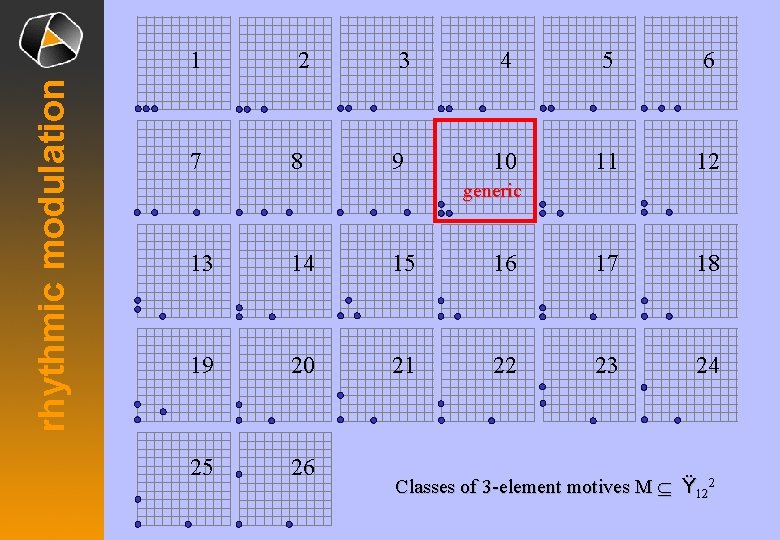
rhythmic modulation 1 2 3 4 5 6 7 8 9 10 11 12 generic 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Classes of 3 -element motives M Í Ÿ 122

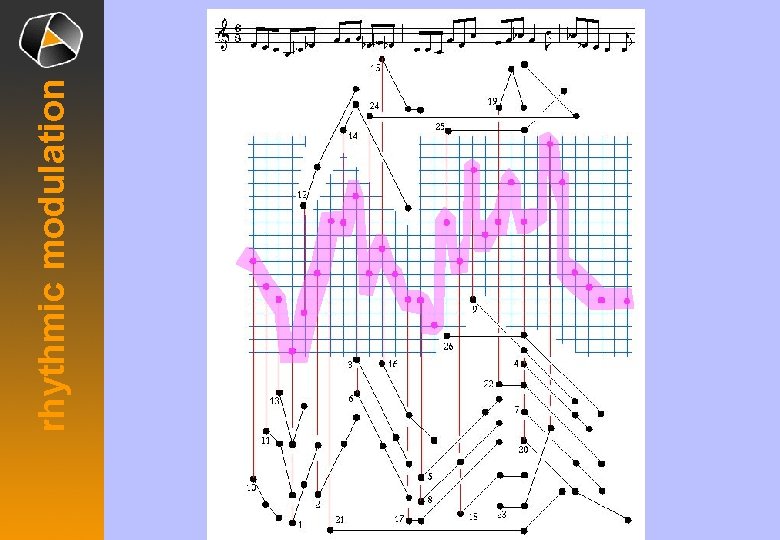
rhythmic modulation

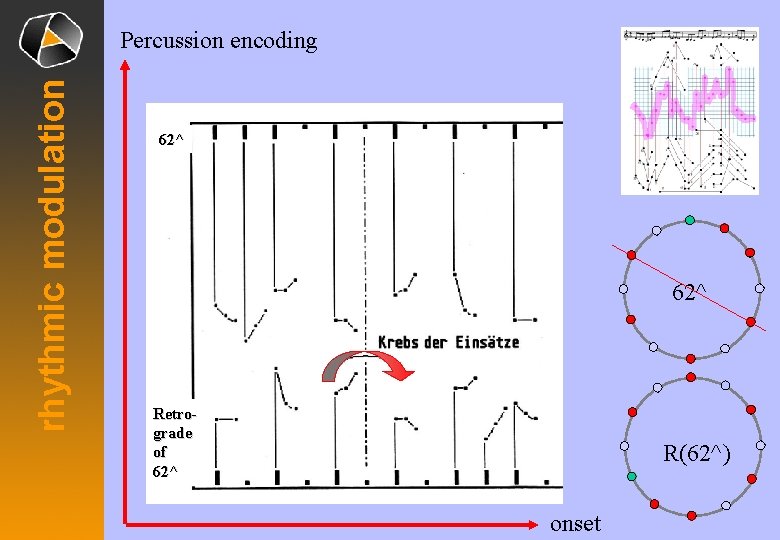
rhythmic modulation Percussion encoding 62^ Retrograde of 62^ R(62^) onset

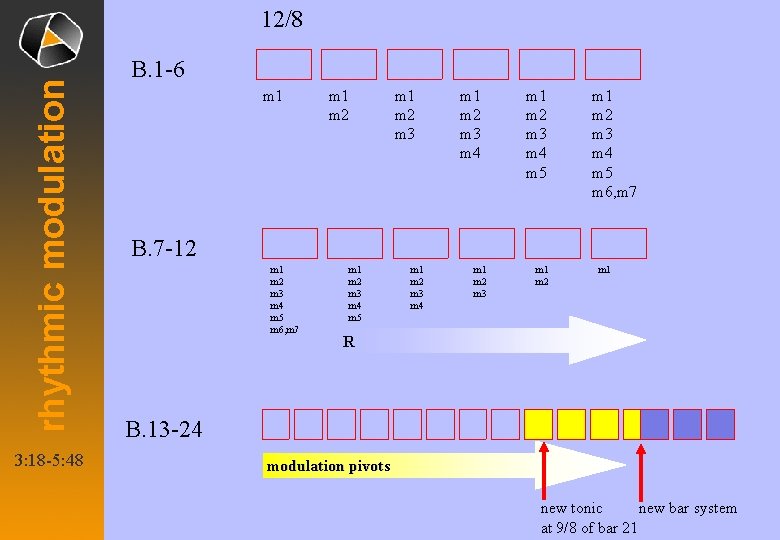
rhythmic modulation 12/8 3: 18 -5: 48 B. 1 -6 m 1 m 2 m 3 m 4 m 1 m 2 m 3 m 4 m 5 m 6, m 7 B. 7 -12 m 1 m 2 m 3 m 4 m 5 m 6, m 7 m 1 m 2 m 3 m 4 m 5 m 1 m 2 m 3 m 4 m 1 m 2 m 3 m 1 m 2 m 1 R B. 13 -24 modulation pivots new bar system new tonic at 9/8 of bar 21