Mathematical Music Theory Status Quo 2000 Guerino Mazzola

Mathematical Music Theory — Status Quo 2000 Guerino Mazzola U & ETH Zürich Internet Institute for Music Science guerino@mazzola. ch www. encyclospace. org

Contents • Time Table • The Concept Framework • Global Classification • Models and Methods • Towards Grand Unification

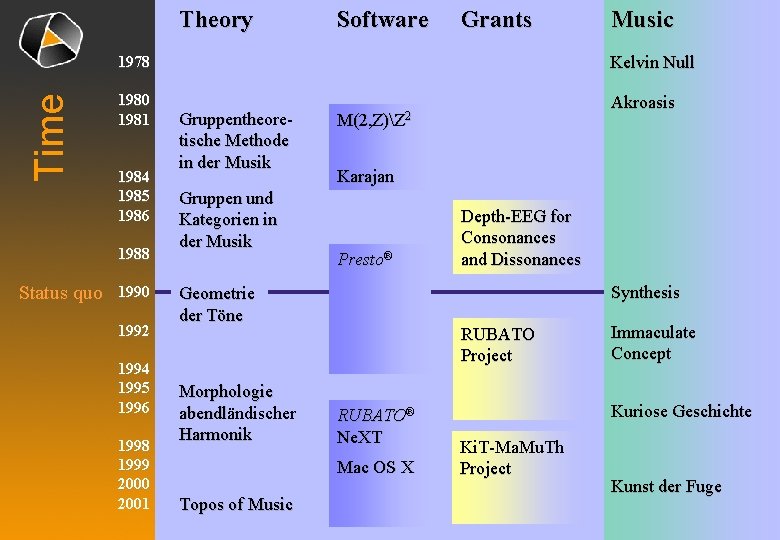
Theory Software Grants Kelvin Null Time 1978 1980 1981 1984 1985 1986 1988 Status quo 1990 1992 1994 1995 1996 1998 1999 2000 2001 Music Gruppentheoretische Methode in der Musik Gruppen und Kategorien in der Musik Karajan Presto® RUBATO Project RUBATO® Ne. XT Mac OS X Topos of Music Depth-EEG for Consonances and Dissonances Synthesis Geometrie der Töne Morphologie abendländischer Harmonik Akroasis M(2, Z)Z 2 Immaculate Concept Kuriose Geschichte Ki. T-Ma. Mu. Th Project Kunst der Fuge

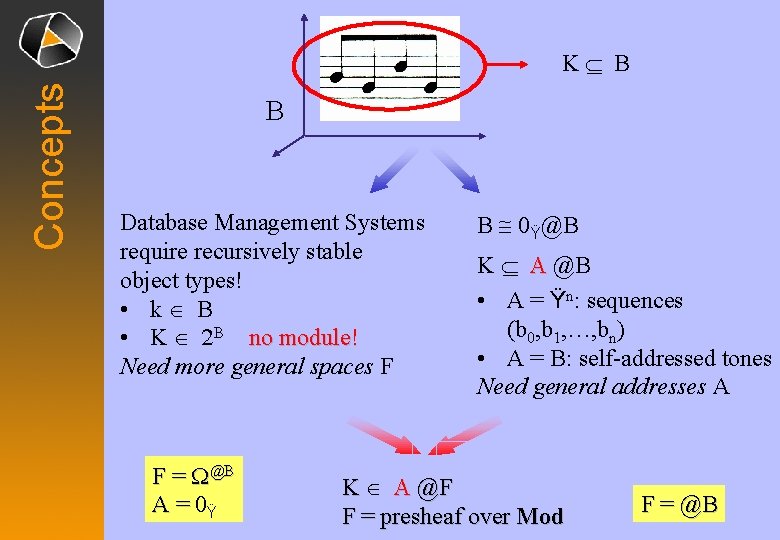
Concepts Mod = category of modules + diaffine morphisms: morphisms • A = R-module, B = S-module • Dilin(A, B) = (l, f) f: A ® B additive, l: R ® S ring homomorphism f(r. a) = l(r). f(a) • eb(x) = b+x; translation on B • A@B = e. B. Dilin(A, B) eb. f: A ® B dilinear translation

Concepts Topos of presheaves over Mod@ = {F: Mod ® Sets, contravariant} Example: representable presheaf @B: @B(A) = A@B F(A) =: A@F A = address Yoneda Lemma The functor @: Mod ® Mod@ is fully faithfull. B ~> @B

Concepts KÍ B B Database Management Systems require recursively stable object types! • kÎ B • K Î 2 B no module! Need more general spaces F F = W@B A = 0Ÿ B @ 0Ÿ@B KÍ A 0Ÿ@B • A = Ÿn: sequences (b 0, b 1, …, bn) • A = B: self-addressed tones Need general addresses A K Î A @F F = presheaf over Mod F = @B

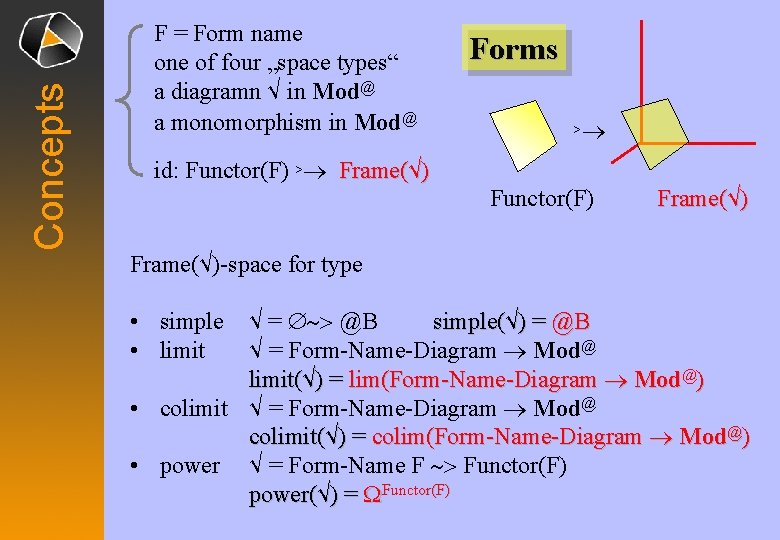
Concepts F = Form name one of four „space types“ a diagramn √ in Mod@ a monomorphism in Mod@ Forms ® > id: Functor(F) >® Frame(√) Functor(F) Frame(√)-space for type √ = Æ~> @B simple(√) = @B √ = Form-Name-Diagram ® Mod@ limit(√) = lim(Form-Name-Diagram ® Mod@) • colimit √ = Form-Name-Diagram ® Mod@ colimit(√) = colim(Form-Name-Diagram ® Mod@) • power √ = Form-Name F ~> Functor(F) power(√) = WFunctor(F) • simple • limit

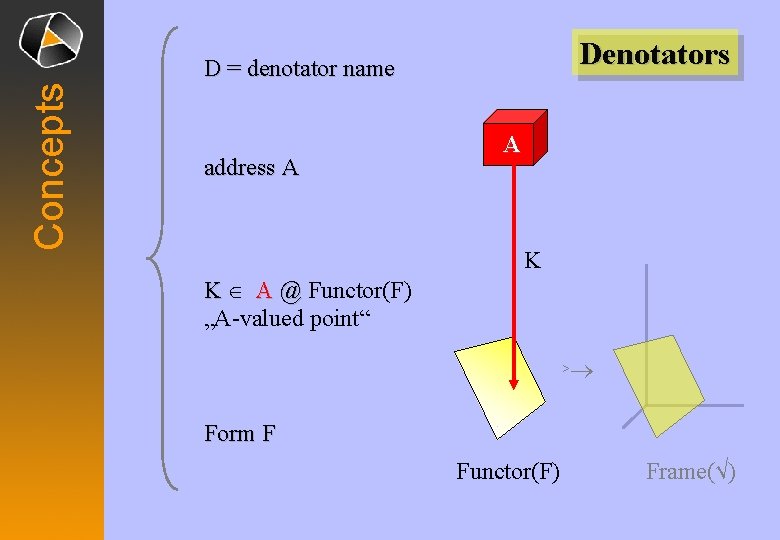
Denotators Concepts D = denotator name address A A K K Î A @ Functor(F) „A-valued point“ ® > Form F Functor(F) Frame(√)

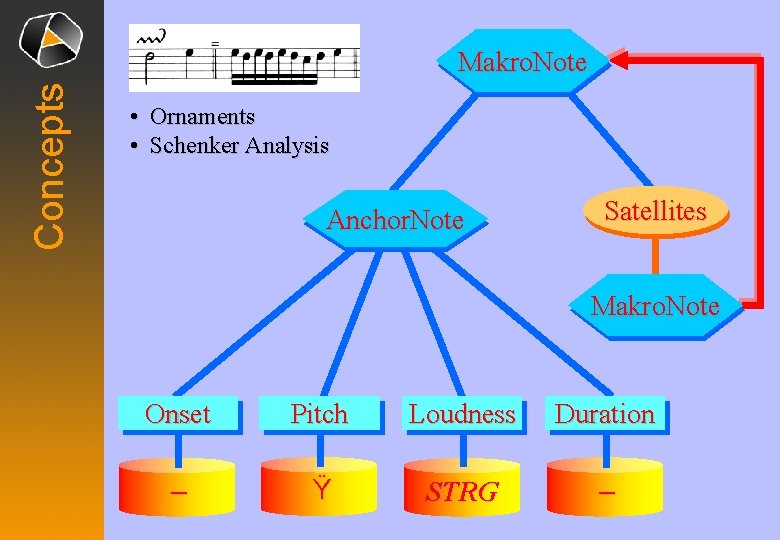
Concepts Makro. Note • Ornaments • Schenker Analysis Anchor. Note Satellites Makro. Note Onset Pitch Loudness Duration – Ÿ STRG –

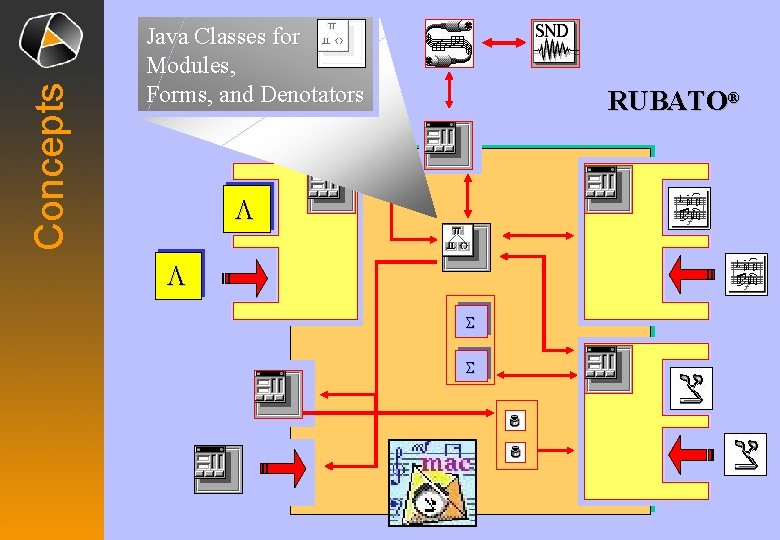
Concepts Java Classes for Modules, Forms, and Denotators RUBATO® L L S S

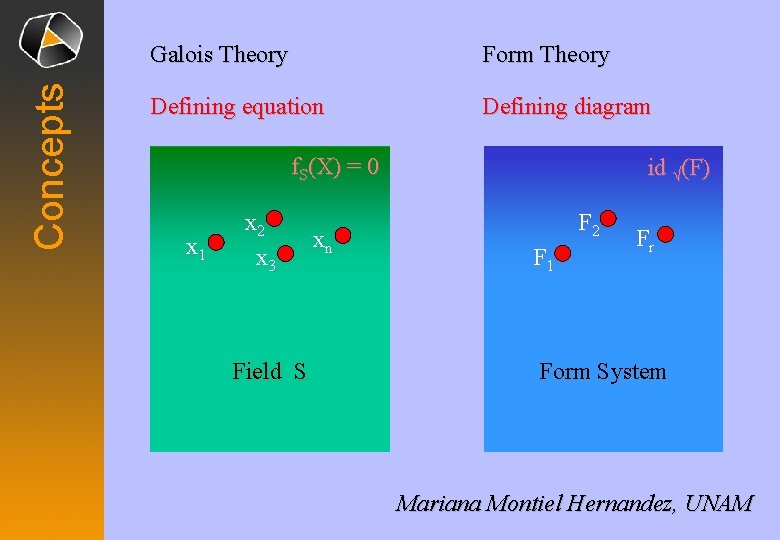
Concepts Galois Theory Form Theory Defining equation Defining diagram f. S(X) = 0 x 1 x 2 x 3 Field S xn id √(F) F 2 F 1 Fr Form System Mariana Montiel Hernandez, UNAM

Classification Category Loc of local compositions Type = Power F ~> Functor(F) = G local composition K Î A@WG objects K Í @A ´�G generalizes K Í A@G „objective“ objective local compositions K Í @A ´�G morphisms f/a @a ´�h L Í @B ´�H a = affine morphism f, h = natural transformations specify „address change“ a

Classification Ob. Loc Embedding functor Trace functor Ob. Loc. A Theorem • Loc is finitely complete (while Ob. Loc is not!) • On Ob. Loc. A and Loc. A Embedding and Trace are an adjoint pair: Ob. Loc. A(Embedding(K), L) @ Loc. A(K, Trace(L))

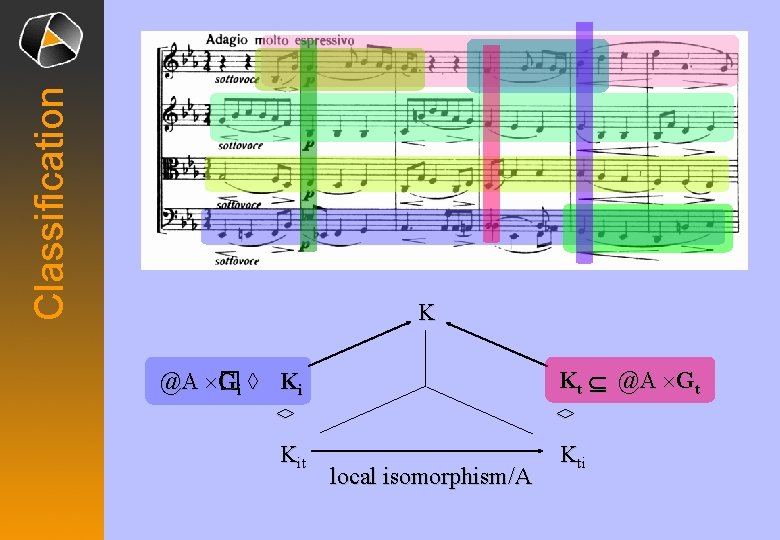
Classification K K Ktt Í Í@ A@ AG ´G t t Gii ◊◊ K Kii @A @ ´G � ◊ ◊ Kit local isomorphism/A Kti

Classification Category Gl of global compositions Objects: KI = functor K which is covered by a finite atlas I = (Ki) of local compositions in Loc. A at address A Morphisms: KI at address A LJ at address B f/a: KI ® LJ f = natural transformation, a: A ® B = address change f induces local morphisms fij/a on the charts

Classification Have Grothendieck topology Cov(Gl) on Gl Covering families (fi/ai: KIi ® LJ)i are finite, generating families. Theorem • Cov(Gl) is subcanonical • The presheaf GF: KI ~> GF(KI) of global affine functions is a sheaf.

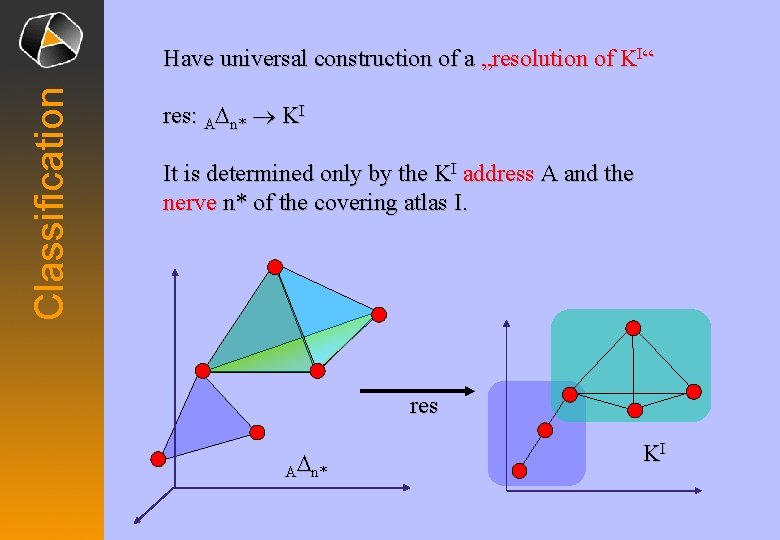
Classification Have universal construction of a „resolution of KI“ res: ADn* ® KI It is determined only by the KI address A and the nerve n* of the covering atlas I. res ADn* KI

Classification Theorem (global addressed geometric classification) Let A = locally free of finie rank over commutative ring R Consider the objective global compositions KI at A with (*): • locally free chart modules R. Ki • the function modules GF(Ki) are projective (i) Then KI can be reconstructed from the coefficient system of retracted functions res*F(KI) Í F(ADn*) (ii) There is a subscheme Jn* of a projective R-scheme of finite type whose points w: Spec(S) ® Jn* parametrize the isomorphism classes of objective global compositions at address SƒRA with (*).

Classification Applications of classification: • String Quartet Theory: Why four strings? • Composition: Generic compositional material • Performance Theory: Why deformation?

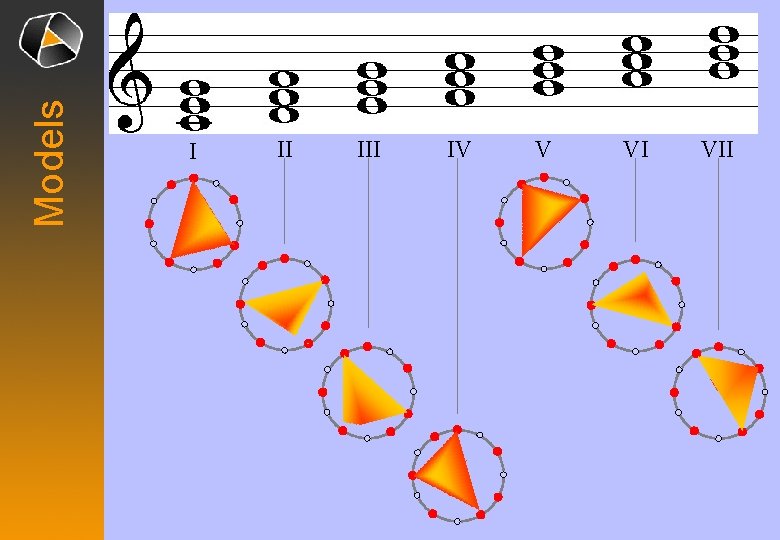
Models There are models for these musicological topics Mazzola • Tonal modulation in well-tempered and just intonation and general scales Mazzola/Noll • Classical Fuxian counterpoint rules • Harmonic function theory Noll • String quartet theory • Performance theory Ferretti • Melody and motive theory Nestke • Metrical and rhythmical structures • Canons • Large forms (e. g. sonata scheme) Noll • Enharmonic identification

Models What is a mathematical model of a musical phenomenon? Music Mathematics Field of Concepts Precise Concept Framework Material Selection Instance specification Process Type Formal process restatement Grown rules for process • construction and • analysis Proof of structure theorems Why this material, these rules, relations? Deduction of rules from structure theorems Generalization! Anthropomorphic Principle!

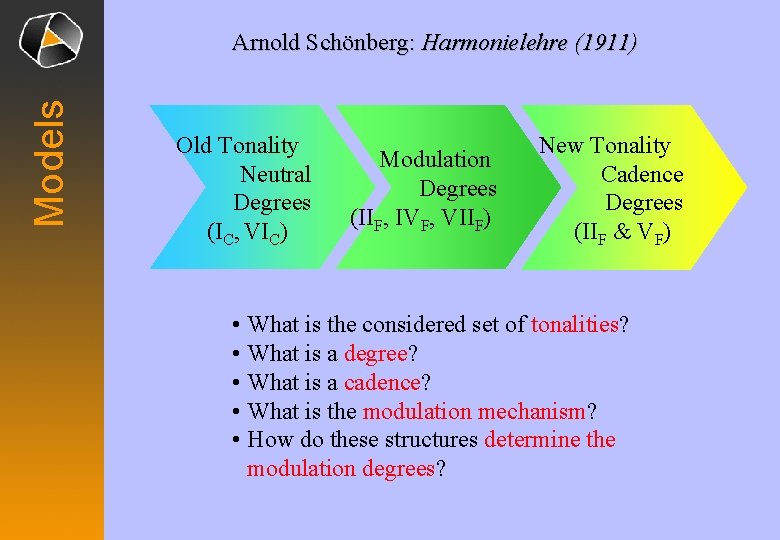
Models Arnold Schönberg: Harmonielehre (1911) Old Tonality Neutral Degrees (IC, VIC) Modulation Degrees (IIF, IVF, VIIF) New Tonality Cadence Degrees (IIF & VF) • What is the considered set of tonalities? • What is a degree? • What is a cadence? • What is the modulation mechanism? • How do these structures determine the modulation degrees?

Models I II IV V VI VII

Models gluon W+ g strong force weak force electromagnetic force graviton gravitation quantum = set of pitch classes = M S(3) T(3) force = symmetry between S(3) and T(3) k k

IVC IIEb Models VIIEb IIC M(3) VC C(3) VIIC VE b IIIEb E b(3)

Unification Ÿ 12 @ Ÿ 3 x Ÿ 4 ƒ 1 Ÿ 12[e] K = Ÿ 12 +e. {0, 3, 4, 7, 8, 9} = consonances e e. 2. 5 D = Ÿ 12 +e. {1, 2, 5, 6, 10, 11} = dissonances

Unification Rules of Counterpoint Following J. J. Fux C/D Symmetry in Human Depth-EEG Extension to Exotic Interval Dichotomies

D = C-dominant triad T = C-tonic triad K ƒ 1 Z 12[e] Trans(D, T) = Trans(K, K)|ƒe Z 12 @ Z 12 ƒe Z 12 [e] @ Z 12 [e]

The Topos of Music Geometric Logic of Concepts, Theory, and Performance in collaboration with Moreno Andreatta, Jan Beran, Chantal Buteau, Karlheinz Essl, Roberto Ferretti, Anja Fleischer, Harald Fripertinger, Jörg Garbers, Stefan Göller, Werner Hemmert, Mariana Montiel, Andreas Nestke, Thomas Noll, Joachim Stange-Elbe, Oliver Zahorka www. encylospace. org