The Other Polyhedra Steven Janke Colorado College Five

The Other Polyhedra Steven Janke Colorado College

Five Regular Polyhedra Dodecahedron Tetrahedron Icosahedron Octahedron Cube

Prehistoric Scotland Carved stones from about 2000 B. C. E.

Roman Dice ivory stone

Roman Polyhedra Bronze, unknown function

Radiolaria drawn by Ernst Haeckel (1904)

Theorem: Let P be a convex polyhedron whose faces are congruent regular polygons. Then the following are equivalent: 1. 2. 3. 4. 5. The vertices of P all lie on a sphere. All the dihedral angles of P are equal. All the vertex figures are regular polygons. All the solid angles are congruent. All the vertices are surrounded by the same number of faces.

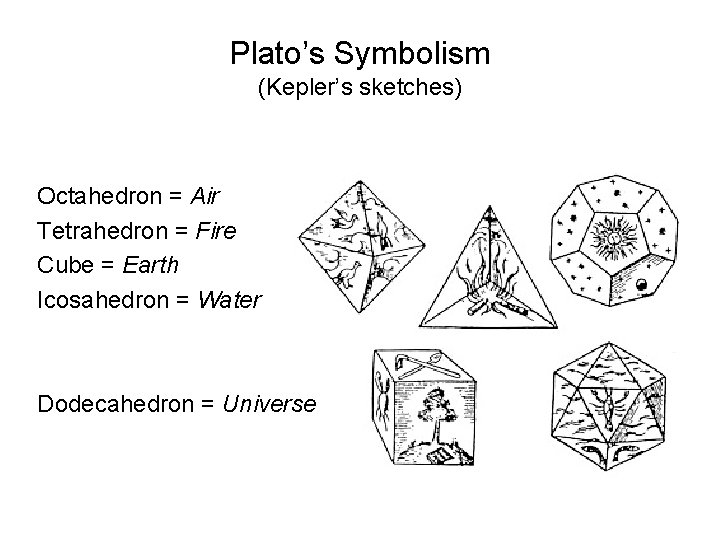
Plato’s Symbolism (Kepler’s sketches) Octahedron = Air Tetrahedron = Fire Cube = Earth Icosahedron = Water Dodecahedron = Universe

Theorem: There are only five convex regular polyhedra. (Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron) Proof: In a regular polygon of p sides, the angles are (1 -2/p)π. With q faces at each vertex, the total of these angles must Be less than 2π: q(1 -2/p)π < 2π 1/p + 1/q > 1/2 Only solutions are: (3, 3) (3, 4) (4, 3) (3, 5) (5, 3)

Johannes Kepler (1571 -1630) (detail of inner planets)

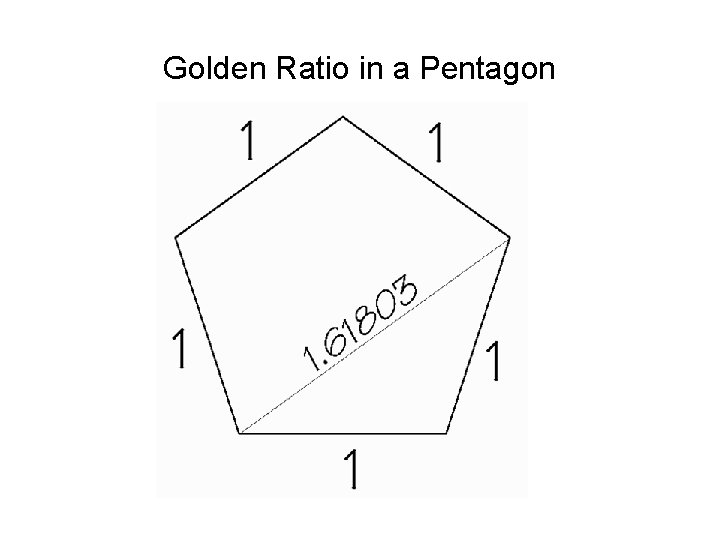
Golden Ratio in a Pentagon

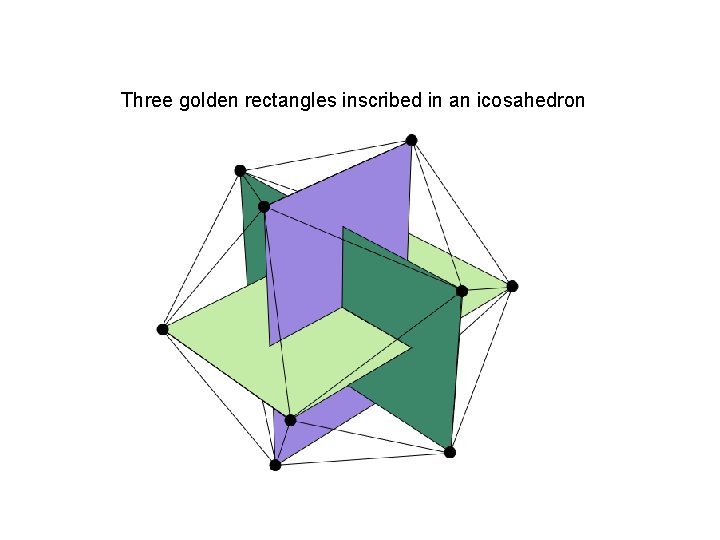
Three golden rectangles inscribed in an icosahedron

Euler’s Formula: V + F = E + 2 Vertices Faces Edges Tetrahedron 4 4 6 Cube 8 6 12 Octahedron 6 8 12 Dodecahedron 20 12 30 Icosahedron 12 20 30 Duality: Vertices Faces

Regular Polyhedra Coordinates: Cube: (± 1, ± 1) Tetrahedron: (1, 1, 1) (1, -1) (-1, 1) Octahedron: (± 1, 0, 0) (0, ± 1, 0) (0, 0, ± 1) Iscosahedron: (0, ±φ, ± 1) (± 1, 0, ±φ) (±φ, ± 1, 0) Dodecahedron: (0, ±φ-1, ±φ) (±φ, 0, ±φ-1) (±φ-1, ±φ, 0) (± 1, ± 1) Where φ2 - φ - 1 = 0 giving φ = 1. 618 … (Golden Ratio)

Portrait of Luca Pacioli (1445 -1514) (by Jacopo de Barbari (? ) 1495)

Basilica of San Marco (Venice) (Floor Pattern in Marble) Possibly designed by Paolo Uccello in 1430

Albrecht Durer (1471 -1528) Melancholia I, 1514

Church of Santa Maria in Organo, Verona (Fra Giovanni da Verona 1520’s)

Leonardo da Vinci (1452 -1519) Illustrations for Luca Pacioli's 1509 book The Divine Proportion

Leonardo da Vinci “Elevated” Forms

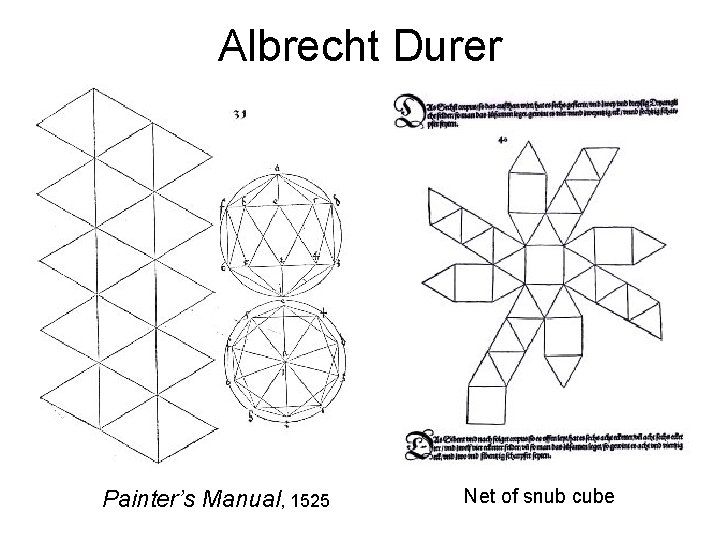
Albrecht Durer Painter’s Manual, 1525 Net of snub cube

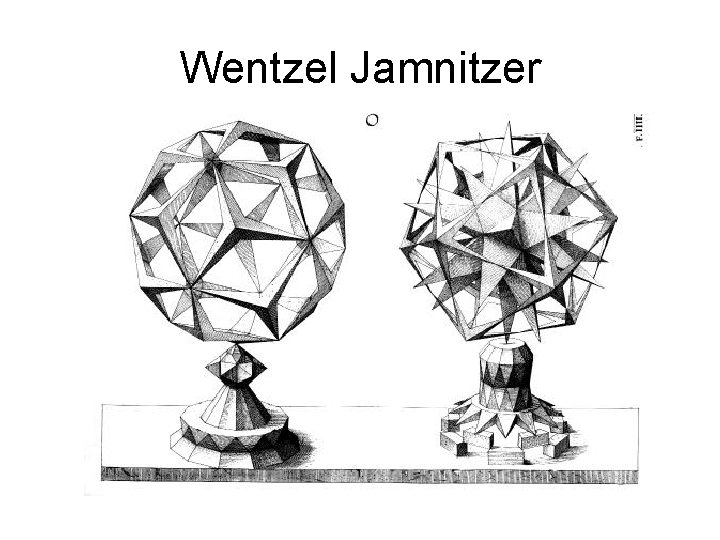
Wentzel Jamnitzer (1508 -1585) Perspectiva Corporum Regularium, 1568

Wentzel Jamnitzer

Theorem: The only finite rotation groups are: Cyclic Dihedral Tetrahedral (alternating group of degree 4) Octahedral Icosahedral (alternating group of degree 5)

Lorenz Stoer Geometria et Perspectiva, 1567

Lorenz Stoer Geometria et Perspectiva, 1567

Jean Cousin Livre de Perspective, 1560

Jean-Francois Niceron Thaumaturgus Opticus, 1638

Tomb of Sir Thomas Gorges Salisbury Cathedral, 1635

M. C. Escher (1898 -1972) Stars, 1948

M. C. Escher Waterfall, 1961

M. C. Escher Reptiles, 1943

Order and Chaos M. C. Escher

Regular Polygon with 5 sides

Johannes Kepler Harmonice Mundi, 1619

Theorem: There are only four regular star polyhedra. Small Stellated Dodecahedron (5/2, 5) Great Dodecahedron (5, 5/2) Great Stellated Dodecahedron (5/2, 3) Great Icosahedron (3, 5/2)

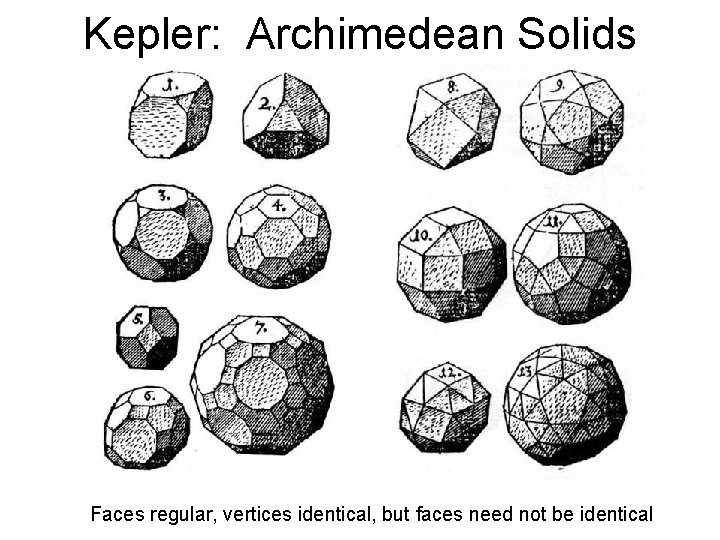
Kepler: Archimedean Solids Faces regular, vertices identical, but faces need not be identical

Lemma: Only three different kinds of faces can occur at each vertex of a convex polyhedra with regular faces. Theorem: The set of convex polyhedra with regular faces and congruent vertices contains only the 13 Archimedean polyhedra plus two infinite families: the prisms and antiprisms.

Max Brückner Vielecke und Vielflache, 1900

Historical Milestones 1. Theatetus (415 – 369 B. C. ): Octahedron and Icosahedron. 2. Plato (427 – 347 B. C. ): Timaeus dialog (five regular polyhedra). 3. Euclid (323 -285 B. C. ): Constructs five regular polyhedra in Book XIII. 4. Archimedes (287 -212 B. C. ): Lost treatise on 13 semi-regular solids. 5. Kepler (1571 - 1630): Proves only 13 Archimedean solids. 6. Euler (1707 -1783): V+F=E+2 7. Poinsot (1777 -1859): Four regular star polyhedra. Cauchy proved. 8. Coxeter (1907 – 2003): Regular Polytopes. 9. Johnson, Grunbaum, Zalgaller (1969): Prove 92 polyhedra with regular faces. 10. Skilling (1975): Proves there are 75 uniform polyhedra.

Retrosnub Ditrigonal Icosidodecahedron (a. k. a. Yog Sothoth) (Vertices: 60; Edges: 180; Faces: 100 triangles + 12 pentagrams

References: Coxeter, H. S. M. – Regular Polytopes 1963 Cromwell, Peter – Polyhedra 1997 Senechal, Marjorie, et. al. – Shaping Space 1988 Wenninger, Magnus – Polyhedron Models 1971 Cundy, H. and Rollett, A. – Mathematical Models 1961

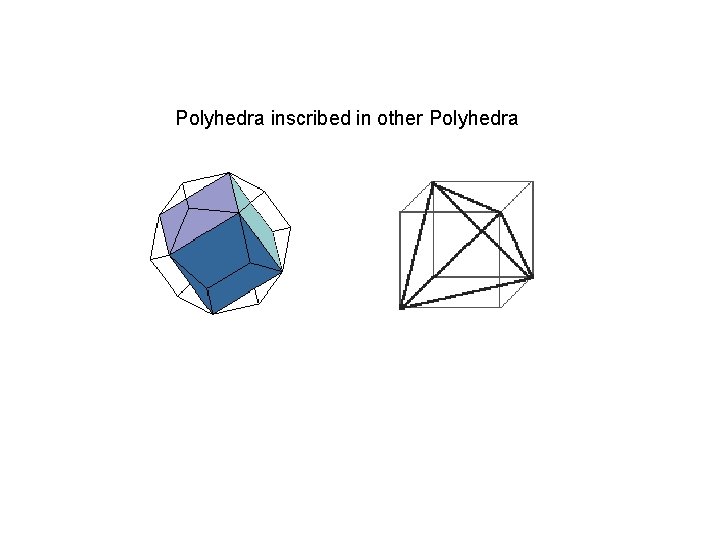
Polyhedra inscribed in other Polyhedra