Ray Tracing Polyhedra Anthony Steed 1999 2003 1

Ray Tracing Polyhedra ©Anthony Steed 1999 -2003 1

Overview Barycentric coordinates n Ray-Polygon Intersection Test n Affine Transformations n 2

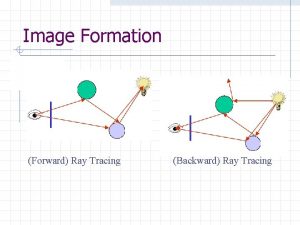
Line Equation n Recall that given p 1 and p 2 in 3 D space, the straight line that passes between is: for any real number t n This is a simple example of a barycentric combination 3

A Barycentric Combination is n a weighted sum of points, where weight sum to 1. • Let p 1, p 2, …, pn be points • Let a 1, a 2, …, an be weights 4

Implications If p 1, p 2, …, pn are co-planar points then p as defined will be inside the polygon defined by the points n Plenty of diagrams n 5

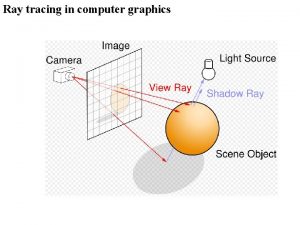
Outline of Polygon Ray Tracing n Three steps • Does the ray intersect the plane of the polygon? – i. e. is the ray not orthogonal to the plane normal • Intersect ray with plane • Test whether intersection point lies within polygon on the plane 6

Does the ray intersect the plane? Ray eq. is p 0 + t. d n Plane eq. is n. (x, y, z) = k n n Then test is n. d !=0 7

Where does it intersect? n Substitute line equation into plane equation n Solve for t n Find pi 8

Is this point inside the polygon? n If it is then it can be represented in barycentric co-ordinates. n Many tests are possible • Winding number (can be done in 3 D) • Infinite ray test (done in 2 D) • Half-space test (done in 2 D for convex poylgons) 9

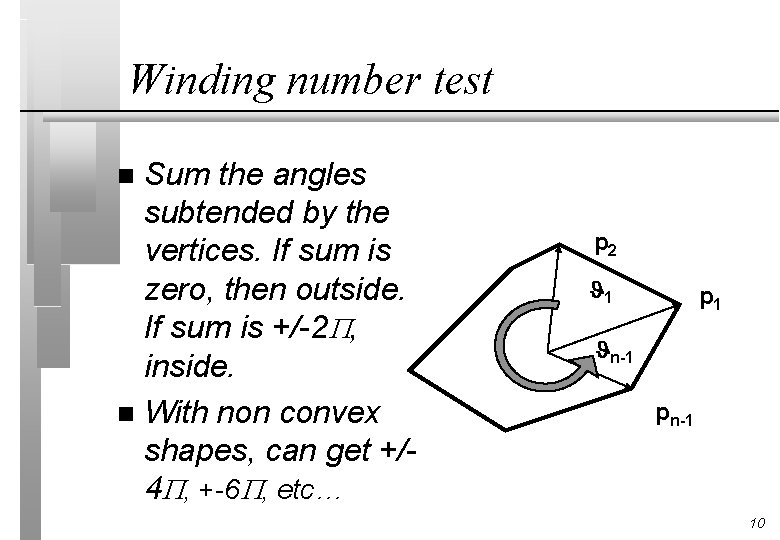
Winding number test Sum the angles subtended by the vertices. If sum is zero, then outside. If sum is +/-2 , inside. n With non convex shapes, can get +/4 , +-6 , etc… n p 2 1 p 1 n-1 pn-1 10

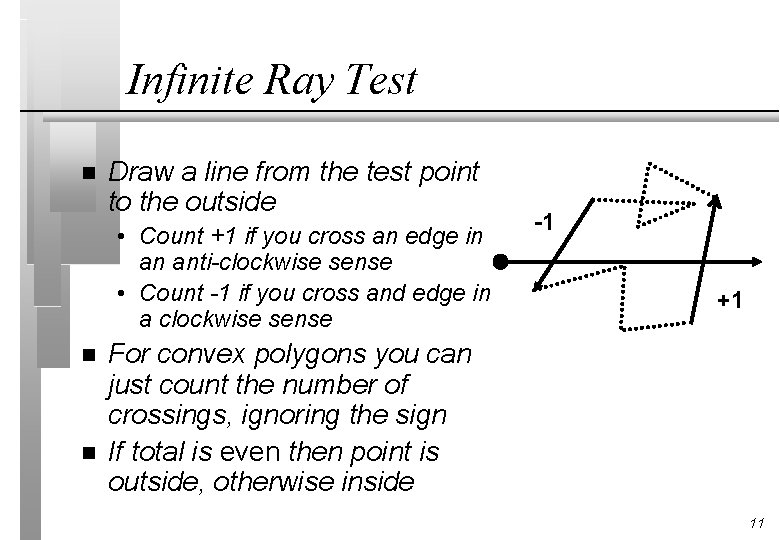
Infinite Ray Test n Draw a line from the test point to the outside • Count +1 if you cross an edge in an anti-clockwise sense • Count -1 if you cross and edge in a clockwise sense n n -1 +1 For convex polygons you can just count the number of crossings, ignoring the sign If total is even then point is outside, otherwise inside 11

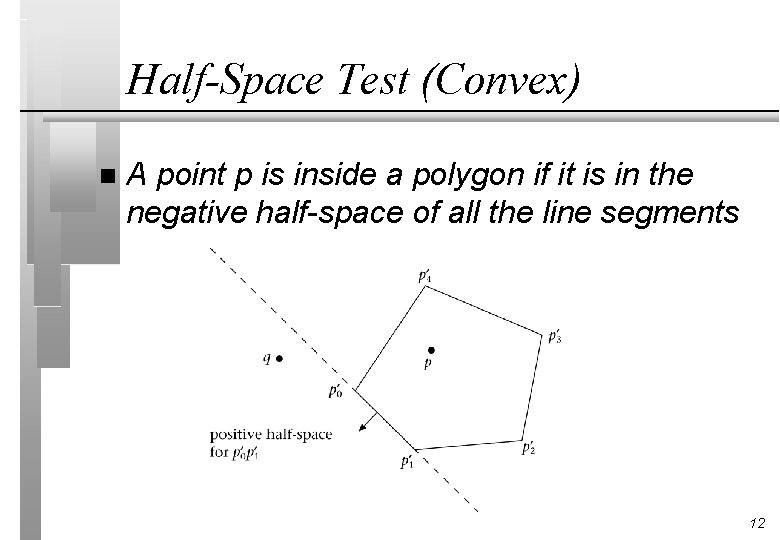
Half-Space Test (Convex) n A point p is inside a polygon if it is in the negative half-space of all the line segments 12

Transformations Revisited Homogenous transform as described is affine n Preserves barycentric co-ordinates n n f is affine iff f (p ) = å a i f (pi ) n i =1 n p = åa i pi i =1 n åa i =1 13

To Show Transformation is Affine Unit vectors e 1=(1 0 0), e 2=(0 1 0), e 3=(0 0 1) and e 4=(0 0 0) n p=(x 1 x 2 x 3) n Let x 4=1 -x 2 -x 3 n Thus n 14

. . . n But for unit vectors, mapping is easy to derive 15

… n So combine those two 16

. . . n But we know x 4=1 -x 2 -x 3 17

. . . n Expand that, remembering what ei is n But this is the matrix transformation 18

Why? If a rotation, scale, translation are affine then barycentricity is preserved n If barycentricity is preserved then polygons are still flat after transformation n 19

Recap Lines and polygons (and volumes) can be determined in terms of barycentric coordinates n We have shown that homogenous transformations are, by definition, affine n This polygons remain “flat” n Thus we now can use arbitrary transformations on polyhedra n 20