Ray Tracing Polyhedra Anthony Steed 1999 2005 1

Ray Tracing Polyhedra ©Anthony Steed 1999 -2005 1

Overview Barycentric coordinates n Ray-Polygon Intersection Test n Affine Transformations n 2

Line Equation n Recall that given p 1 and p 2 in 3 D space, the straight line that passes between is: for any real number t n This is a simple example of a barycentric combination 3

A Barycentric Combination is n a weighted sum of points, where weight sum to 1. • Let p 1, p 2, …, pn be points • Let a 1, a 2, …, an be weights 4

Implications If p 1, p 2, …, pn are co-planar points then p as defined will be inside the polygon defined by the points n Proof of this is out of scope, but a few diagrams should convince you of the outline of a proof … n 5

Ray Tracing a Polygon n Three steps • Does the ray intersect the plane of the polygon? – i. e. is the ray not orthogonal to the plane normal • Intersect ray with plane • Test whether intersection point lies within polygon on the plane 6

Does the ray intersect the plane? Ray eq. is p 0 + t. d n Plane eq. is n. (x, y, z) = k n n Then test is n. d !=0 7

Where does it intersect? n Substitute line equation into plane equation n Solve for t n Find pi 8

Is this point inside the polygon? n n n If it is then it can be represented in barycentric co-ordinates There are potentially several barycentric combinations Many tests are possible • Winding number (can be done in 3 D) • Infinite ray test (done in 2 D) • Half-space test (done in 2 D for convex poylgons) 9

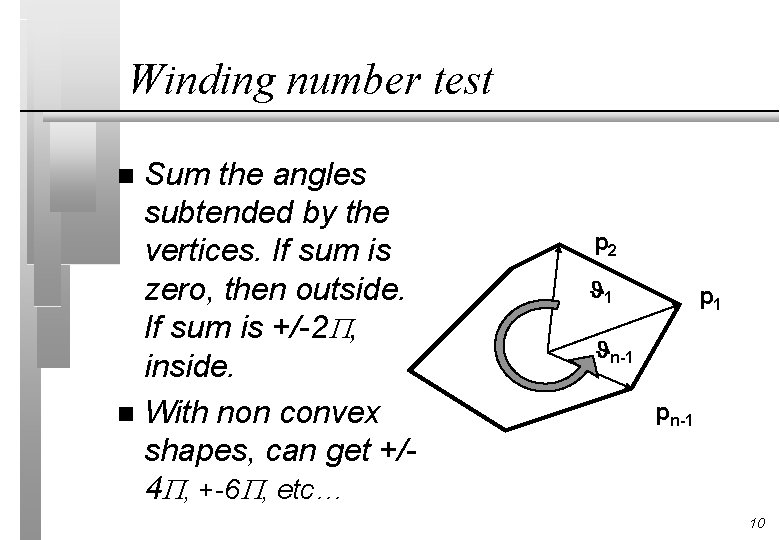
Winding number test Sum the angles subtended by the vertices. If sum is zero, then outside. If sum is +/-2 , inside. n With non convex shapes, can get +/4 , +-6 , etc… n p 2 1 p 1 n-1 pn-1 10

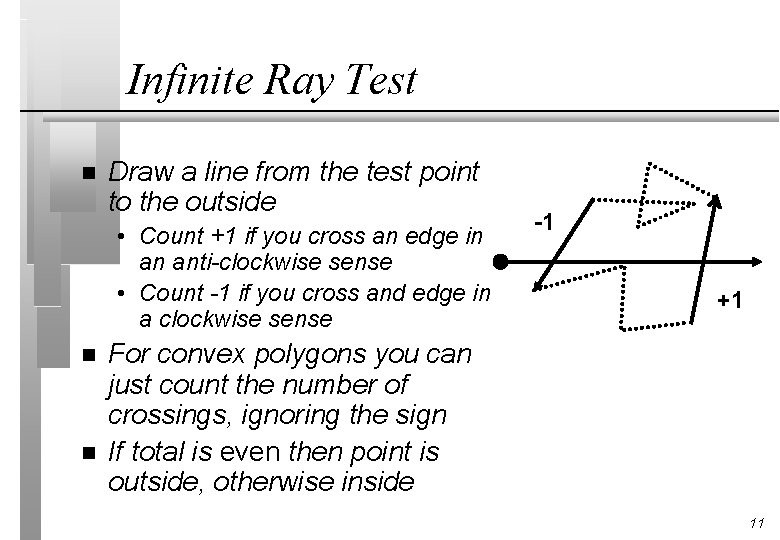
Infinite Ray Test n Draw a line from the test point to the outside • Count +1 if you cross an edge in an anti-clockwise sense • Count -1 if you cross and edge in a clockwise sense n n -1 +1 For convex polygons you can just count the number of crossings, ignoring the sign If total is even then point is outside, otherwise inside 11

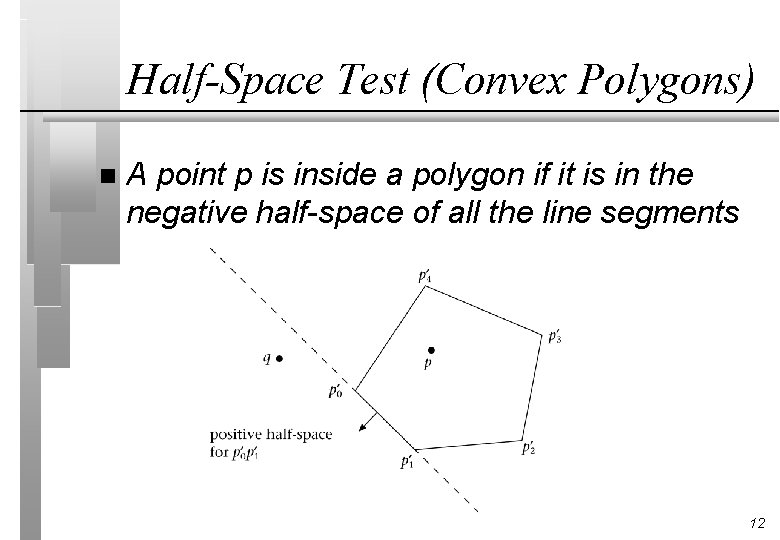
Half-Space Test (Convex Polygons) n A point p is inside a polygon if it is in the negative half-space of all the line segments 12

Note That the winding angle and half-space tests only tell you if the point is inside the polygon, they do not get you a barycentric combination n With some minor extensions, its easy to show that the infinite ray test finds a barycentric combination. n 13

Transforming Polygons n n Although its sort of “obvious” that transformations of object preserve flatness and shape, we need to convince ourselves of something specific: that barycentric coordinates are preserved under affine transformations If they weren’t it would be extremely hard to shade and texture polygons later on in the course If a rotation, scale, translation are affine then barycentricity is preserved If barycentricity is preserved then polygons are still “flat” after transformation 14

Transformations Revisited Homogenous transform as described is affine n Preserves barycentric co-ordinates n f is affine iff n 15

To Show Transformation is Affine Unit vectors e 1=(1 0 0), e 2=(0 1 0), e 3=(0 0 1) and e 4=(0 0 0) n p=(x 1 x 2 x 3) n Let x 4=1 -x 2 -x 3 n Thus n 16

. . . n But for unit vectors, mapping is easy to derive 17

… n So combine those two 18

. . . n But we know x 4=1 -x 2 -x 3 19

. . . n Expand that, remembering what ei is n But this is the matrix transformation 20

Recap Lines and polygons (and volumes) can be determined in terms of barycentric coordinates n We have shown that homogenous transformations are, by definition, affine n This polygons remain “flat” n Thus we now can use arbitrary transformations on polyhedra n 21