Matchings Matroids and Polyhedra for Approximating the Travelling

Matchings, Matroids and Polyhedra for Approximating the Travelling Salesman Problem András Sebő CNRS (G-SCOP), Univ. Grenoble Alpes

The Salesman and the Postman The (Travelling) Salesman Nodes = Cities Do all the cities and come back ! NP-hard (Karp, 1972) The (Chinese) Postman Edges = streets Do all the streets and come back ! In P (Edmonds, Johnson 1973)

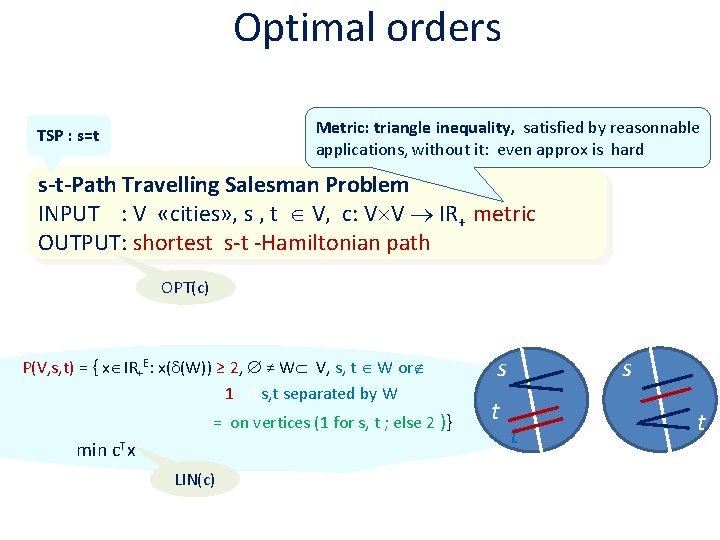
Optimal orders Metric: triangle inequality, satisfied by reasonnable applications, without it: even approx is hard TSP : s=t s-t-Path Travelling Salesman Problem INPUT : V «cities» , s , t V, c: V V IR+ metric OUTPUT: shortest s-t -Hamiltonian path OPT(c) P(V, s, t) = { x IR+E: x( (W)) ≥ 2, ≠ W V, s, t W or 1, if s, t separated by W = on vertices (1 for s, t ; else 2 )} min c. Tx LIN(c) s s t t t

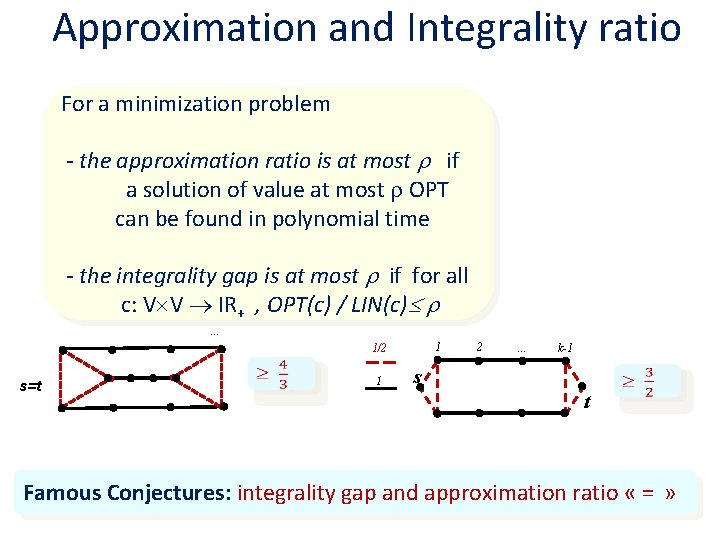
Approximation and Integrality ratio For a minimization problem - the approximation ratio is at most if a solution of value at most OPT can be found in polynomial time - the integrality gap is at most if for all c: V V IR+ , OPT(c) / LIN(c) . . . 1 1/2 s=t 1 2 . . . k-1 s t Famous Conjectures: integrality gap and approximation ratio « = »

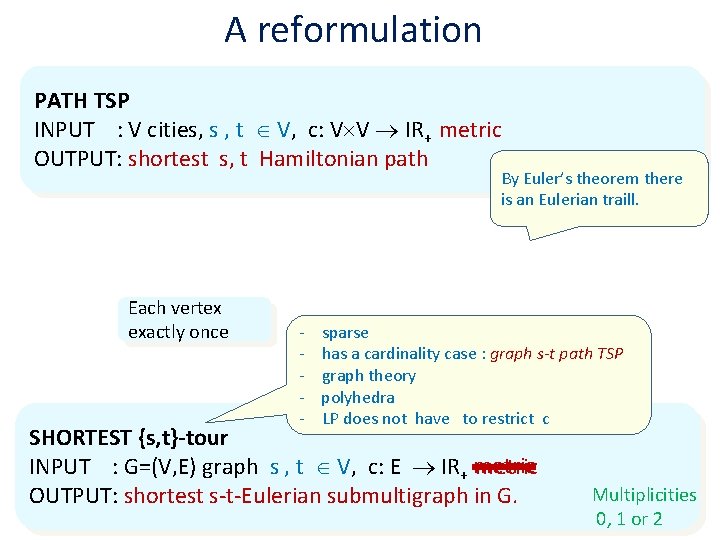
A reformulation PATH TSP INPUT : V cities, s , t V, c: V V IR+ metric OUTPUT: shortest s, t Hamiltonian path , s , t , s Each vertex exactly once By Euler’s theorem there is an Eulerian traill. at least once - sparse + degree parity - has a cardinality case : graph s-t path TSP , t - graph theory - polyhedra - LP does not have to restrict c SHORTEST {s, t}-tour INPUT : G=(V, E) graph s , t V, c: E IR+ metric OUTPUT: shortest s-t-Eulerian submultigraph in G. Multiplicities 0, 1 or 2

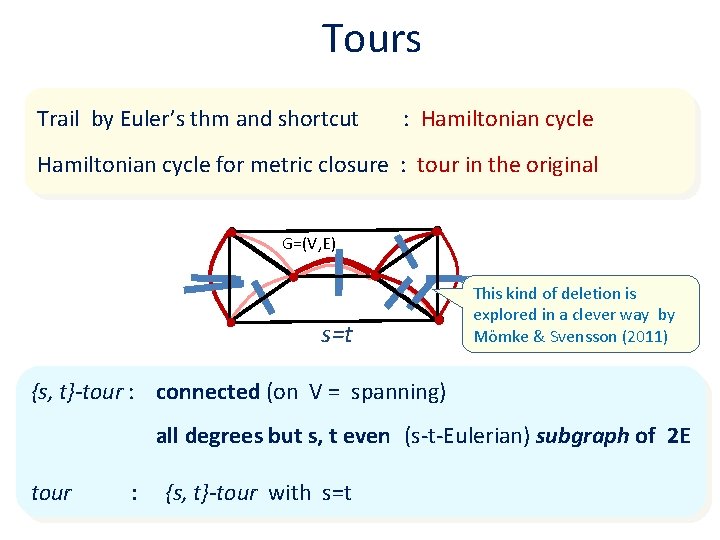
Tours Trail by Euler’s thm and shortcut : Hamiltonian cycle for metric closure : tour in the original G=(V, E) s=t This kind of deletion is explored in a clever way by Mömke & Svensson (2011) {s, t}-tour : connected (on V = spanning) all degrees but s, t even (s-t-Eulerian) subgraph of 2 E tour : {s, t}-tour with s=t

m et ric s

Summary of improvements 2012 -2017 TSP, s-t-path TSP Graph and general versions

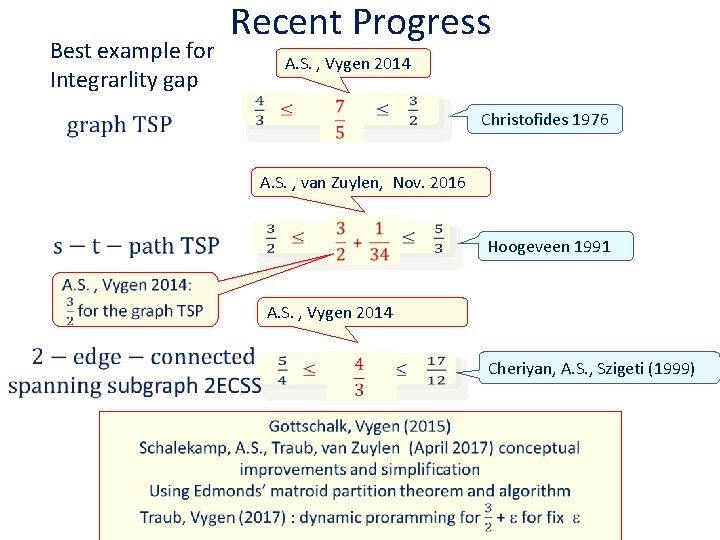
Best example for Integrarlity gap Recent Progress A. S. , Vygen 2014 Christofides 1976 A. S. , van Zuylen, Nov. 2016 Hoogeveen 1991 A. S. , Vygen 2014 Cheriyan, A. S. , Szigeti (1999)

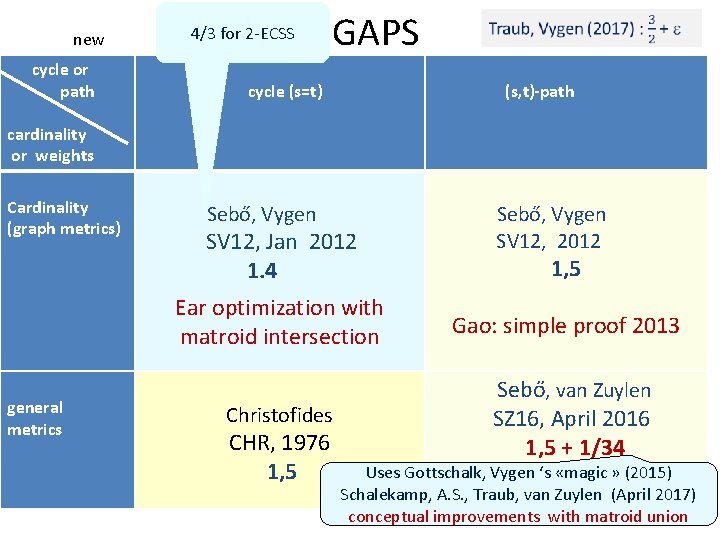
GAPS past cycle or path cycle (s=t) cardinality or weights Cardinality (graph metrics) general metrics Gamarnik, Lewenstein, Sviridenko (2005): 3/2 - for cubic 3 -connected Boyd, Sitters, van der Ster, Stougie (2011): 4/3 for cubic Oveis, Gharan, Saberi, Singh (2011) : 3/2 - Mömke, Svensson (2011) : 1. 461… Mucha (2011) : 13/9=1. 444… (s, t)-path Hoogeveen (1991) 5/3 An, Kleinberg, Shmoys 2011 1. 578 … Hoogeveen (1991) 5/3 Christofides CHR, 1976 1. 5 An, Kleinberg, Shmoys 2011 “AKS” 1. 619 … Sebő (2012), 1. 6 Vygen(2015) 1. 599 Vygen(2016) 1. 566

4/3 for 2 -ECSS new cycle or path GAPS cycle (s=t) (s, t)-path cardinality or weights Cardinality (graph metrics) Sebő, Vygen SV 12, Jan 2012 Gao: simple proof , march 2013 Sebő, Vygen SV 12, 2012 1, 5 1. 4 Ear optimization with matroid intersection 3 2 Gao: simple proof 2013 1 4 general metrics Christofides CHR, 1976 1, 5 Sebő, van Zuylen SZ 16, April 2016 1, 5 + 1/34 Uses Gottschalk, Vygen ‘s «magic » (2015) Schalekamp, A. S. , Traub, van Zuylen (April 2017) conceptual improvements with matroid union

1 Matchings “Parity Correction” for cardinality cases of the TSP, s-t-path TSP and 2 -ECSS

The perfect matching polytope Def : G=(V, E) undirected graph. M E perfect matching (p. m. ) if the sets of endpoints of M partition V. Kőnig (1916) Jacobi (1890) Egerváry (1931) Birkhoff (1946) von Neuman (1952): If G is bipartite : conv ( M : M p. m. ) = {x IRE : x ( (v))=1, x 0 } If G is arbitrary : Edmonds (1965), add : if U V , |U| is odd x ( (U)) 1

Well-known interpretation as probability distribution Particular distributions (max entropy, or comb. restrictions)

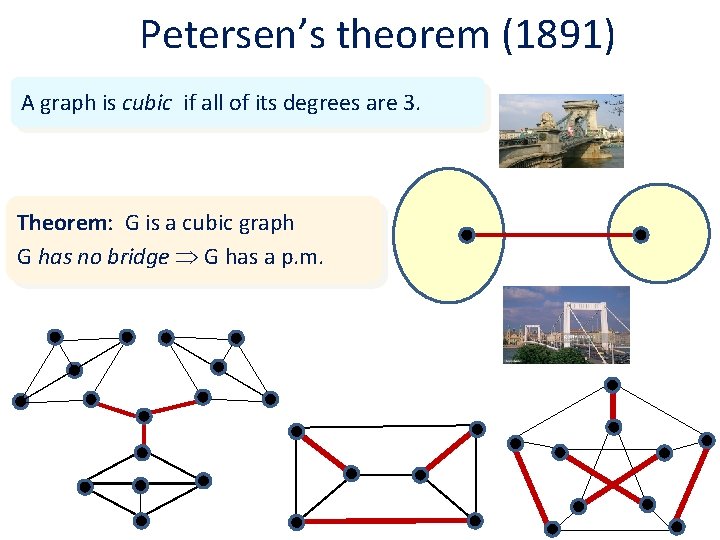
Petersen’s theorem (1891) A graph is cubic if all of its degrees are 3. Theorem: G is a cubic graph G has no bridge G has a p. m.

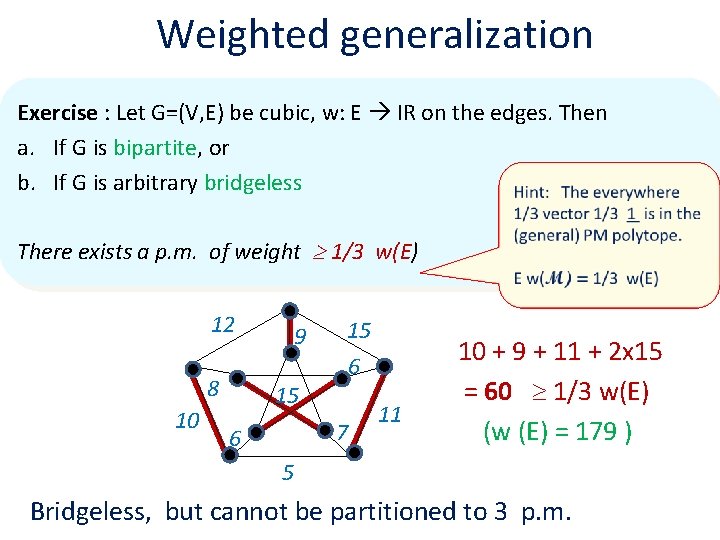
Weighted generalization Exercise : Let G=(V, E) be cubic, w: E IR on the edges. Then a. If G is bipartite, or b. If G is arbitrary bridgeless There exists a p. m. of weight 1/3 w(E) 12 8 10 9 15 15 6 7 6 11 10 + 9 + 11 + 2 x 15 = 60 1/3 w(E) (w (E) = 179 ) 5 Bridgeless, but cannot be partitioned to 3 p. m.

A generalization of Matchings: T-joins, parity correction for the TSP J E(G) is a T-join, if T = set of odd degree vertices of J. Adding or deleting edges of J ( 1 in multiplicity) : v T The parity changes exactly in T Approximation and Integrality Gap for the TSP (Christofides-Wolsey) separates the problem into connectivity + parity correction

The parity correction polyhedron J G S G connected, |T| even T-join T : = V (= odd degree vertices of F) Theorem Edmonds, Johnson ’ 73 : conv (T-joins) + IR+n = Q+(G, T) : = {x IR+E x( (W)) ≥ 1, (W) is a T-cut, i. e. |W T| is odd} Trick : If x Q+(G, T), then c(modifying parity in T) ≤ c. T x

Christofides : connectivity & parity correction Christofides Tour : c-min spannicng tree F + parity correction (pc) TF-joins, where TF : ={v: d. F(v) is odd } Can be delet ed diconnect F s tour TF-join is a TF-join => pc ≤ 1/2 for (s, t)-tours 2/3 Wolsey ‘ 80 : x* P(G, s=t) , so x*/2 Q+(G, T) T, apply to T=TF

Thm : Christofides-type alg ≤ 5/3 -OPTLP c. Tx : = LIN , E[F ]=x F F(s, t) Proof: + gap E[F F(s, t )] = q = x - p corrects the parity (x + p) /2 is in Q+ x - p E[parity correction] ≤ p: = E[F(s, t)] TF F s {s, t} –join of F G t {s, t} TF -join

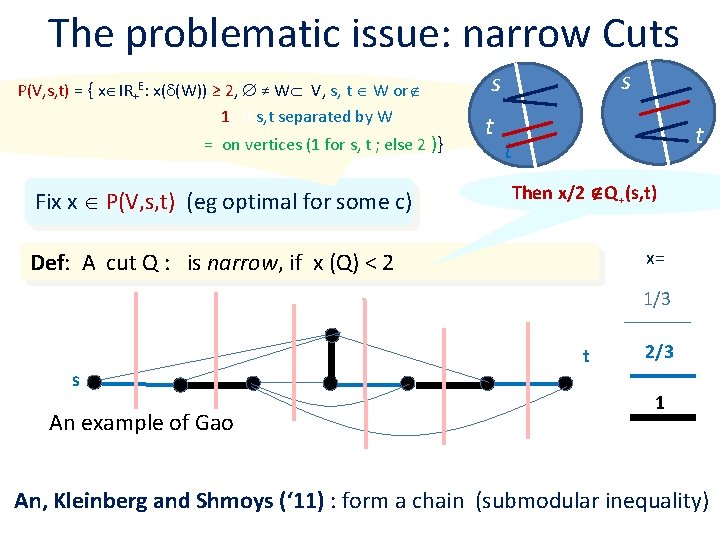
The problematic issue: narrow Cuts P(V, s, t) = { x IR+E: x( (W)) ≥ 2, ≠ W V, s, t W or 1, if s, t separated by W = on vertices (1 for s, t ; else 2 )} Fix x P(V, s, t) (eg optimal for some c) s s t t t Then x/2 Q+(s, t) x= Def: A cut Q : is narrow, if x (Q) < 2 1/3 s An example of Gao t 2/3 1 An, Kleinberg and Shmoys (‘ 11) : form a chain (submodular inequality)

2 Matroids Ears : connectivity anticipating parity correction, Graph TSP with matroid intersection General s-t-path TSP with matroid union Delta-matroids and uniform covers in 3

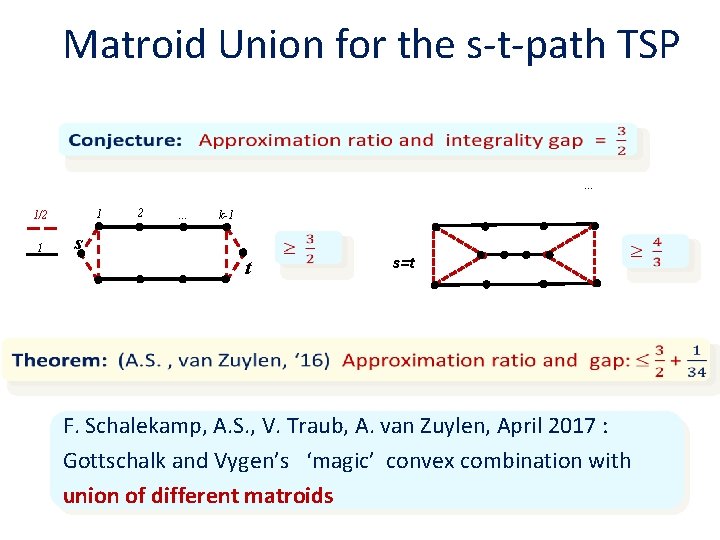
Matroid Union for the s-t-path TSP . . . 1 1/2 1 2 . . . k-1 s t s=t F. Schalekamp, A. S. , V. Traub, A. van Zuylen, April 2017 : Gottschalk and Vygen’s ‘magic’ convex combination with union of different matroids

2 ECSS Minimum cardinality 2 -Edge Connected Spanning Subgraph-TSP, graph-TSP paths Def: A graph G=(V, E) is 2 -edge-connected, if (V, E e ) is connected for all e E.

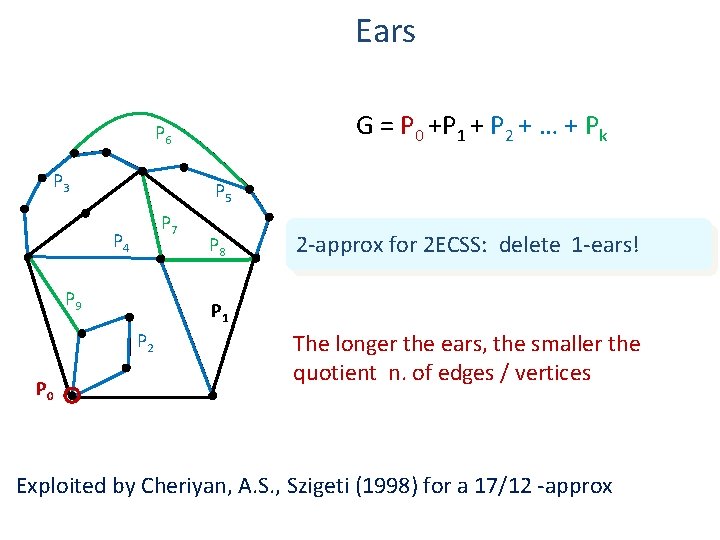
Ears G = P 0 +P 1 + P 2 + … + Pk P 6 P 3 P 5 P 7 P 4 P 9 2 -approx for 2 ECSS: delete 1 -ears! P 1 P 2 P 0 P 8 The longer the ears, the smaller the quotient n. of edges / vertices Exploited by Cheriyan, A. S. , Szigeti (1998) for a 17/12 -approx

Approximation of 2 -ECSS, graph-TSP paths Theorem: (A. S. , Jens Vygen, 2014 ) 2 -ECSS of cardinality 4/3 OPTLP 4/3 OPT of Graph-TSP 7/5 OPTLP of Graph s-t-path-TSP 3/2 OPTLP Sketch of algorithmic proof : 1. Find an ear-decomposition Minimizing the number of even ears (Frank, 1993), - Which include 2 -ears, - there is no other lower bound for the number of nontrivial ears.

Ear-splicing Cheriyan, A. S. , Szigeti (1998), A. S. , Vygen (2014) 2. Do ear-splicing until reaching a nice ear-decomposition, that is: - 1 -ears last, 2 -ears, 3 -ears «pendant» : only trivial ears (edges) come later - no edges between their inner vertices, - min number of even ears Advantage of 2 - and 3 -ears : their parity is ready for the TSP there is freedom to add any variant

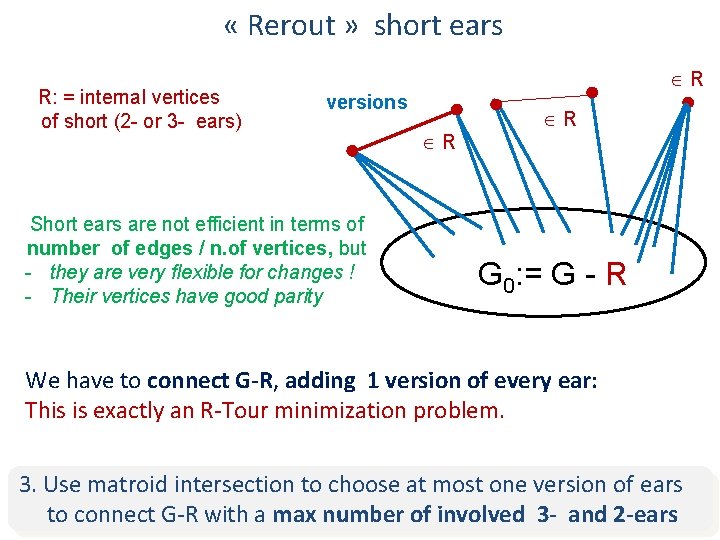
« Rerout » short ears R: = internal vertices of short (2 - or 3 - ears) R versions Short ears are not efficient in terms of number of edges / n. of vertices, but - they are very flexible for changes ! - Their vertices have good parity R R G 0: = G - R We have to connect G-R, adding 1 version of every ear: This is exactly an R-Tour minimization problem. 3. Use matroid intersection to choose at most one version of ears to connect G-R with a max number of involved 3 - and 2 -ears

Matroid Intersection, Union Edmonds (1970) M = (S, F 1) , M = (S, F 2) matroids conv ( F : F Fi) = {x IRS : x (A) ri (A) for all A S } Max { |F| : F F 1 F 2 } max { 1 T x : x (A) ri (A) (i=1, 2) for all A S } Theorem (Edmonds 1970): max |F| = min r 1 (X) + r 2 (S X) F F 1 F 2 X S Polynomial algorithm , weights too, nice version : Frank (1981) Easily equivalent : matroid partition, matroid union, … Schrijver’s book

Exact solution of ear optimization R-Tour Minimization Input : G graph, R V(G), non-negative weights Output : Find a min weight R-Tour , that is, subgraph of 2 G where - all degrees of vertices in R are even - which is connected on V(G) NP-hard : for R=V(G) = the min weight R-tour problem Special case in P: R is an eardrum i. e. the components of G(R) are vertices or edges; weight cardinality. opt V(G) ≥ opt. R : = the opt of this problem

3 Polyhedra : Uniform covers tours, {s, t} tours, ATSP

Uniform Covers with Tours tour : Eulerian (connected , all degrees even) subgraph (V, F), F 2 E Fact : G= (V, E) undirected 3 -edge connected. Then 1 conv ( r : r {0, 1, 2}E is the incidence vector of a tour} Recall Christofides-Wolsey: For the price of ½ LP optimum the parities of degrees of a tree can be corrected. J G F T : = V (= odd degree vertices of F) T-joins Any fixed conv comb defines a tree valued random variable, Proof : 2/3 dominates a point of the spanning tree polytope 1/3 dominates x Edmonds, Johnson’s T –join polyhedron T. E (tree F + parity correction for F, i. e. a TF-join) 2/3 + 1/3

Can 1 be decreased to c < 1 in the ‘Fact’ ? YES: Haddadan, Newman, Ravi (2017) c= 18/19 Famous conjecture : G= (V, E) undirected: x IR+E , x(C) 2 on every cut (subtour elim) , Equivalent through Farkas ‘ Lemma Then 4/3 x conv (tours} (occurs in Carr Vempala 2001 ) Conjecture: G= (V, E) undirected 3 -edge connected, cubic. Then 8/9 conv ( x : x {0, 1, 2}E is the incidence vector of a tour} Sandwich : weaker than Famous, stronger than graph special case. Proof: 2/3 subtour , so using the Famous Conjecture : 4/3 x 2/3 = 8/9 conv (tours} Boyd, A. S. June 26, 2017 (IPCO) : fundamental: M matching G-M =squares <-> compatible Euler = Hamilton -> delta-matroids Theorem : 6/7 < 1 is a conv comb of tours for a `fundamental class’

s-t-tours : Can c > 1 be decreased to 1 ? Famous conjecture : G= (V, E) undirected : x IR+E , x(C) 1 on s-t cuts, 2 otherwise (subtour elimination) Then 3/2 x conv (s-t-tours} Theorem : Conjecture: G/{s, t} 3 -edge-connected. Then 1 conv ( x : x {0, 1, 2}E is the incidence vector of a tour} Proof: 2/3 subtour , so using the Famous Conjecture : 3/2 x 2/3 = 1 conv (tours} ATSP : Constant gap +approx (Svensson, Tarnawski, Végh, August Tour: Eulerian, connected 2017) Conjecture : Integrality gap 2, and approximation multisubgraph Problem : Eulerian, cubic, strongly 3 -arc-conn => tour of cardinality 2 n.

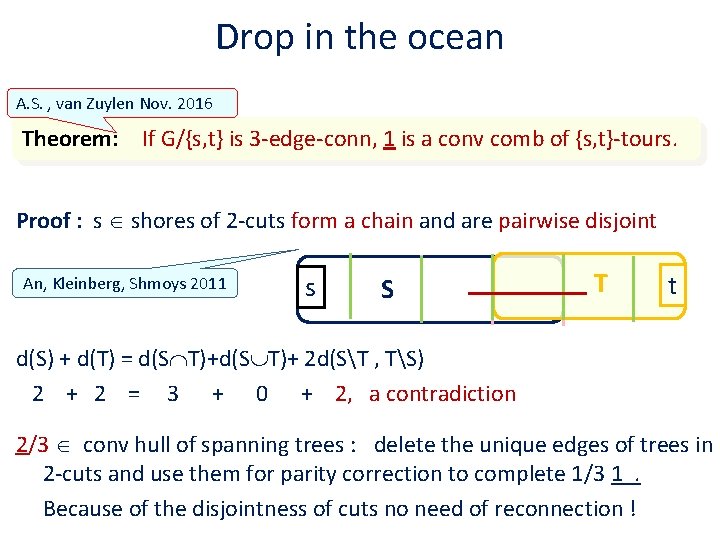
Drop in the ocean A. S. , van Zuylen Nov. 2016 Theorem: If G/{s, t} is 3 -edge-conn, 1 is a conv comb of {s, t}-tours. Proof : s shores of 2 -cuts form a chain and are pairwise disjoint An, Kleinberg, Shmoys 2011 s S T t d(S) + d(T) = d(S T)+ 2 d(ST , TS) 2 + 2 = 3 + 0 + 2, a contradiction 2/3 conv hull of spanning trees : delete the unique edges of trees in 2 -cuts and use them for parity correction to complete 1/3 1 . Because of the disjointness of cuts no need of reconnection !

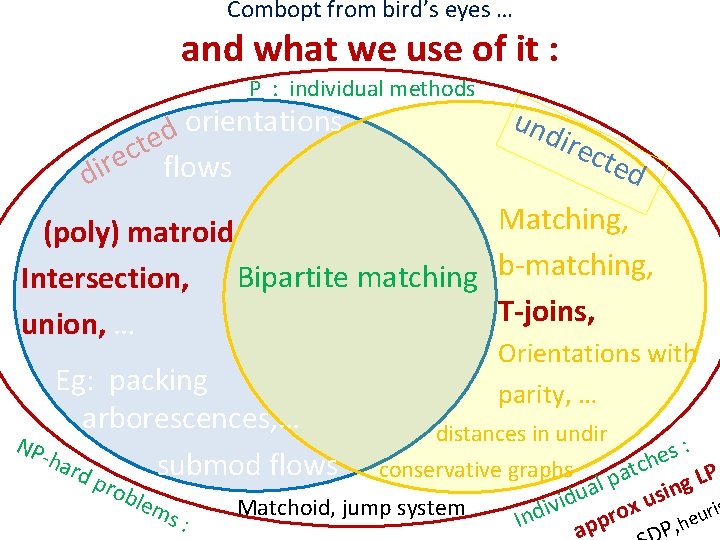
Combopt from bird’s eyes … and what we use of it : P : individual methods orientations d e t c flows e r di und irec ted Matching, (poly) matroid Intersection, Bipartite matching b-matching, T-joins, union, … Orientations with parity, … Eg: packing arborescences, … distances in undir NP : s -h submod flows he ard c t conservative graphs pro pa ing LP l a ble s du i u v i x Matchoid, jump system m ris o u s : r e Ind , h pp a P

NOT YET THE END ! - Ultimate : 4/3 for tours, 3/2 for [s, t}-tours (get rid of 1/34) - direct proof for layered decomposition. Edmonds’ matr union - Uniform cover of 8/9 by tours in 3 -edge-connected cubic graphs - Can 1 be uniformly covered by s, t tours - Do directed Eulerian Trails have tours of size 2 n ? HAPPY BIRTHDAY ! Tom and Jayme