Tema 8 Mtodos de ajuste de curvas regresin

Tema 8 Métodos de ajuste de curvas: regresión lineal y no lineal Fco. Javier Burguillo Universidad de Salamanca Ajuste de curvas

Etapas de una investigación Análisis : tests estadísticos, ajuste de curvas Exploración de datos Obtención datos, calibrados, etc. Diseño de experimentos Antecedentes Bibliográficos Ajuste de curvas

Ajuste de curvas [S] : 1. 2 5. 2 6. 3 7. 2 v : 4. 3 5. 4 7. 2 8. 4 9. 5 v v = f[S] Modelo Empírico En matemáticas: y = f(x) Ajuste de curvas Modelo Teórico

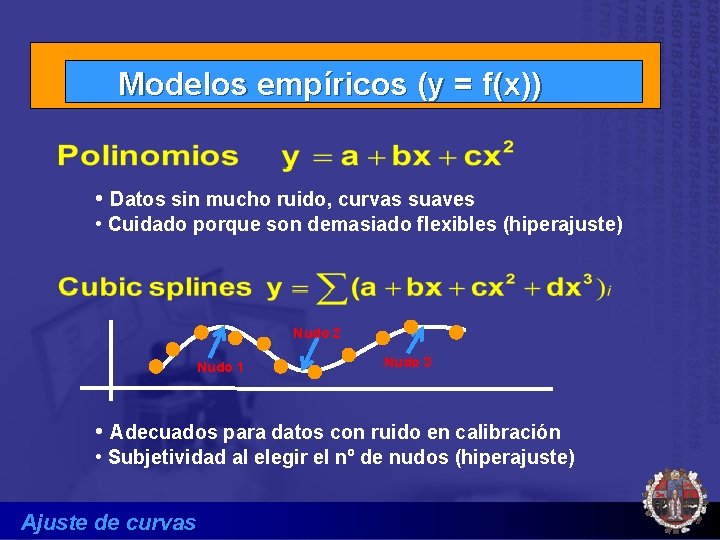
Modelos empíricos (y = f(x)) • Datos sin mucho ruido, curvas suaves • Cuidado porque son demasiado flexibles (hiperajuste) Nudo 2 Nudo 1 Nudo 3 • Adecuados para datos con ruido en calibración • Subjetividad al elegir el nº de nudos (hiperajuste) Ajuste de curvas

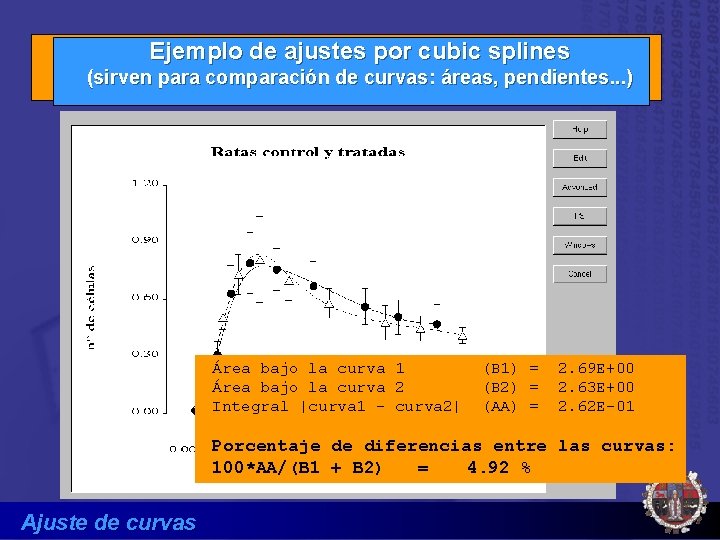
Ejemplo de ajustes por cubic splines (sirven para comparación de curvas: áreas, pendientes. . . ) Área bajo la curva 1 Área bajo la curva 2 Integral |curva 1 - curva 2| (B 1) = (B 2) = (AA) = 2. 69 E+00 2. 63 E+00 2. 62 E-01 Porcentaje de diferencias entre las curvas: 100*AA/(B 1 + B 2) = 4. 92 % Ajuste de curvas

Modelos teóricos En ecuaciones algebraicas Binding +L +L K 1 K 2 En ecuaciones diferenciales Lipasa E fracción de sitios ocupados Ajuste de curvas E*S E* + S E P

Ecuaciones de interés en Biomedicina Decaimientos exponenciales: Suma de Michaelis-Menten: Unión de Ligandos a macromoléculas: Curvas de crecimiento y curvas dosis-respuesta (modelo Logístico): Ajuste de curvas

Otras ecuaciones algebraicas De dos variables y varios parámetros : Ejemplos : Ajuste de curvas

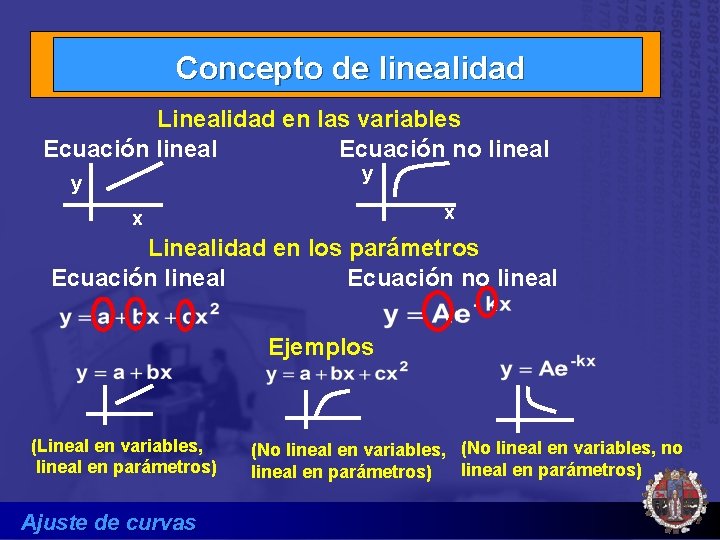
Concepto de linealidad Linealidad en las variables Ecuación lineal Ecuación no lineal y y x x Linealidad en los parámetros Ecuación lineal Ecuación no lineal Ejemplos (Lineal en variables, lineal en parámetros) Ajuste de curvas (No lineal en variables, no lineal en parámetros)

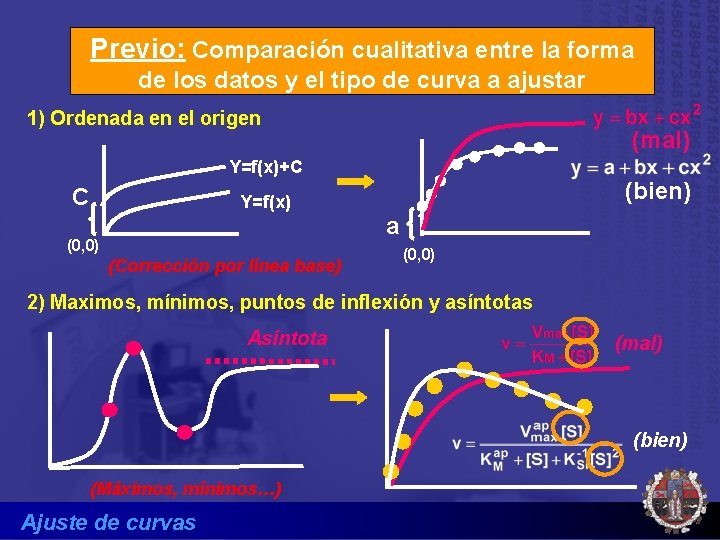
Previo: Comparación cualitativa entre la forma de los datos y el tipo de curva a ajustar 1) Ordenada en el origen (mal) Y=f(x)+C C (bien) Y=f(x) a (0, 0) (Corrección por línea base) (0, 0) 2) Maximos, mínimos, puntos de inflexión y asíntotas Asíntota (mal) (bien) (Máximos, mínimos…) Ajuste de curvas

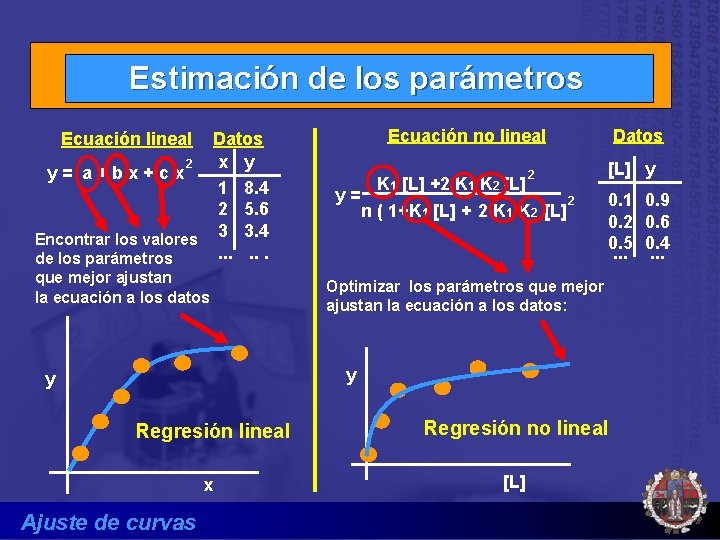
Estimación de los parámetros Datos x y 2 y= a+bx+cx 1 8. 4 2 5. 6 Encontrar los valores 3 3. 4. . . de los parámetros Ecuación no lineal Ecuación lineal que mejor ajustan la ecuación a los datos 2 y= K 1 [L] +2 K 1 K 2 [L] 2 n ( 1+K 1 [L] + 2 K 1 K 2 [L] Datos [L] y 0. 1 0. 2 0. 5. . . Optimizar los parámetros que mejor ajustan la ecuación a los datos: y y Regresión lineal x Ajuste de curvas Regresión no lineal [L] 0. 9 0. 6 0. 4. . .

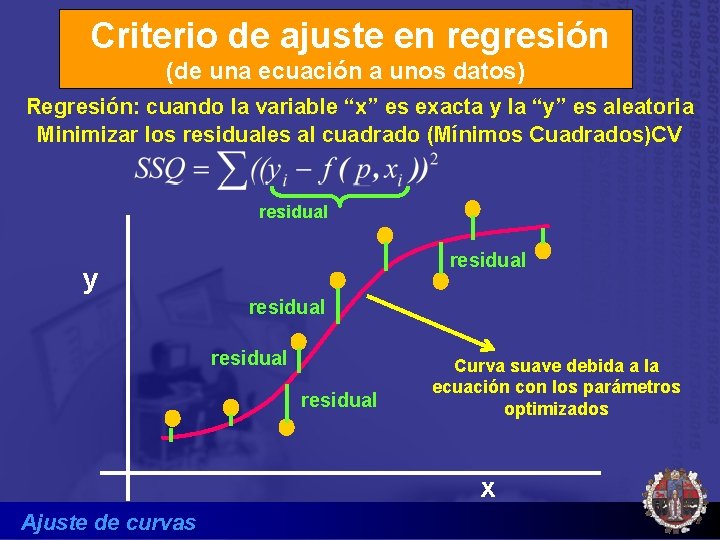
Criterio de ajuste en regresión (de una ecuación a unos datos) Regresión: cuando la variable “x” es exacta y la “y” es aleatoria Minimizar los residuales al cuadrado (Mínimos Cuadrados)CV residual y residual Curva suave debida a la ecuación con los parámetros optimizados x Ajuste de curvas

Regresión por mínimos cuadrados Objetivos Encontrar las mejores estimas de los parámetros Cuantificar precisión parámetros usando límites de confianza Regresión lineal simple (Ecuaciones lineales en los parámetros, por ej. y= a+bx, polinomios en x, …. ) • Se puede explicitar cada parámetro, solución única, método exacto Regresión lineal múltiple Ajuste de curvas Regresión no lineal (Ecuaciones no lineales en parámetros, por ej. y =Ae-kx) • No se pueden explicitar los parámetros, solución aproximada. • Métodos iterativos tipo: “Búsqueda” (Random Search) “Gradiente” (Gauss-Newton)

Cálculos en regresión lineal (simple y múltiple) usando notación matricial Ajuste de curvas

Regresión lineal simple p< 0. 05 , luego los dos parámetros son significativamente distintos de cero Ajuste de curvas

Regresión lineal múltiple Ajuste de curvas

Bondad de un ajuste en regresión lineal (Respecto a los residuales) (Debe de ser pequeño) y (debe ser del orden del error experimental) (R 2 = 0. 95 significaría que el modelo explica el 95% de la variabilidad) Representación de los residuales (deben estar al azar): Residual 0 + - Ajuste de curvas • Test de las rachas • Test de los signos

Bondad de un ajuste en regresión lineal (Respecto a los parámetros) (1/2) Matriz de correlación Ajuste de curvas

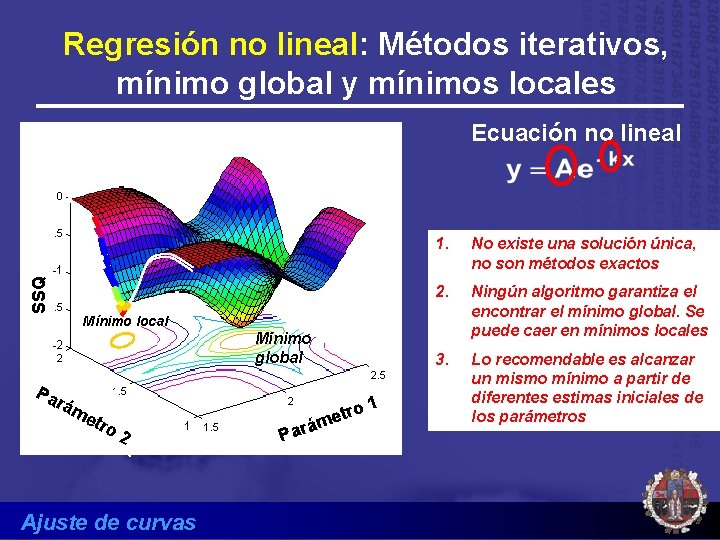
Regresión no lineal: Métodos iterativos, mínimo global y mínimos locales SSQ Ecuación no lineal 1. No existe una solución única, no son métodos exactos 2. Ningún algoritmo garantiza el encontrar el mínimo global. Se puede caer en mínimos locales 3. Lo recomendable es alcanzar un mismo mínimo a partir de diferentes estimas iniciales de los parámetros Mínimo local Mínimo global Pa rám etr o 2 Ajuste de curvas Pa ro t e rám 1

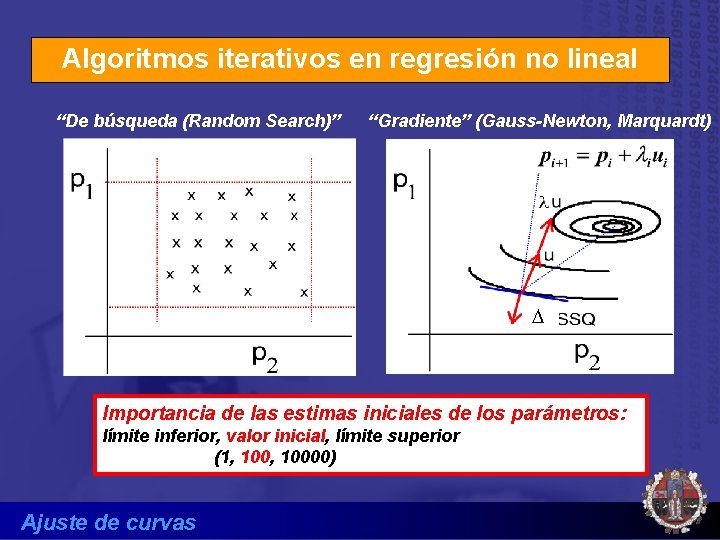
Algoritmos iterativos en regresión no lineal “De búsqueda (Random Search)” “Gradiente” (Gauss-Newton, Marquardt) D Importancia de las estimas iniciales de los parámetros: límite inferior, valor inicial, límite superior (1, 10000) Ajuste de curvas

Bondad de un ajuste en regresión no-lineal • Los parámetros se obtienen por métodos aproximados (iterativos) • No obstante se toma como válida la estadística de la regresión lineal ( sólo cierto en condiciones asintóticas de • Hincapié: la estadística asociada a la regresión no lineal se suele interpretar de una manera más flexible que en la regresión lineal (por ejemplo se admiten coeficientes de variación de los parámetros de hasta el 50%) Ajuste de curvas

Estadística asociada a la regresión no lineal En resumen, lo mismo que en lineal pero con mayor flexibilidad: (n = nº puntos, m = nº parámetros) Ajuste de curvas

Análisis de datos (Ajuste de curvas) Discriminación entre modelos En Ciencias Experimentales lo habitual es que se dude entre modelos alternativos dentro de una secuencia: 1) Es necesario comparar la bondad de los 2 ajustes rivales: SSQ, R 2, distribución residuales, test de las rachas, límites de confianza de los parámetros. . etc 2) Se debe aplicar el test “F”: Estadístico Ajuste de curvas

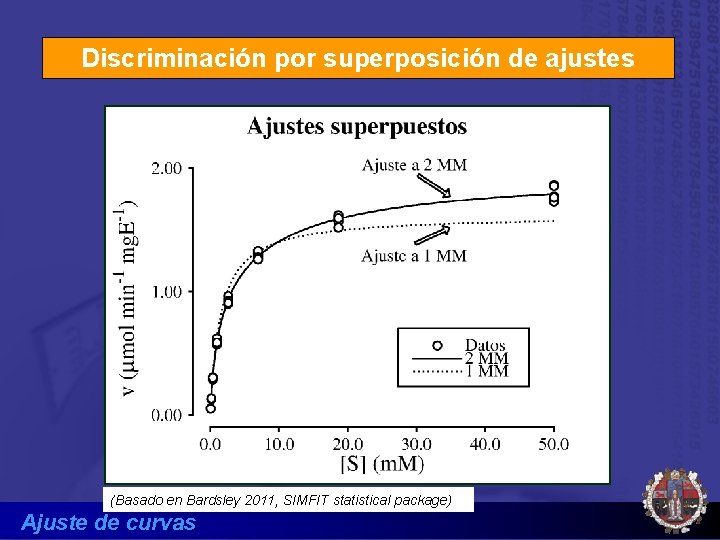
Discriminación por superposición de ajustes (Basado en Bardsley 2011, SIMFIT statistical package) Ajuste de curvas

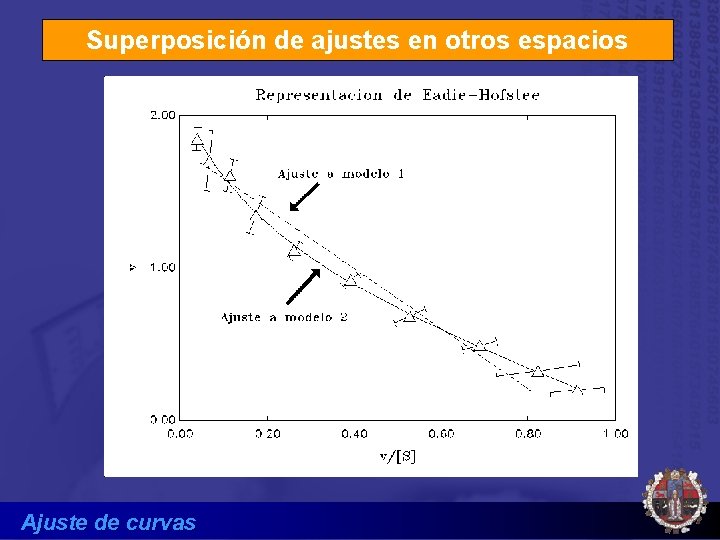
Superposición de ajustes en otros espacios Ajuste de curvas

Regresión con pesos estadísticos • El criterio de mínimos cuadrados asume que: • La variable x no tiene error • El error en la respuesta es aditivo : yi = f ( p , xi ) + u i • Los errores u i y u j son independientes • Todos los errores (ui, u j , . . . ) siguen una distribución normal de media cero y varianza constante (todas las medidas tienen la misma precisión ) • La última suposición no se suele cumplir y hay que “normalizar” los residuales con un factor llamado “peso estadístico”: (estas varianzas se determinan a partir de réplicas) (weight) • El criterio de optimización es ahora : (weighted sum of squares) Ajuste de curvas

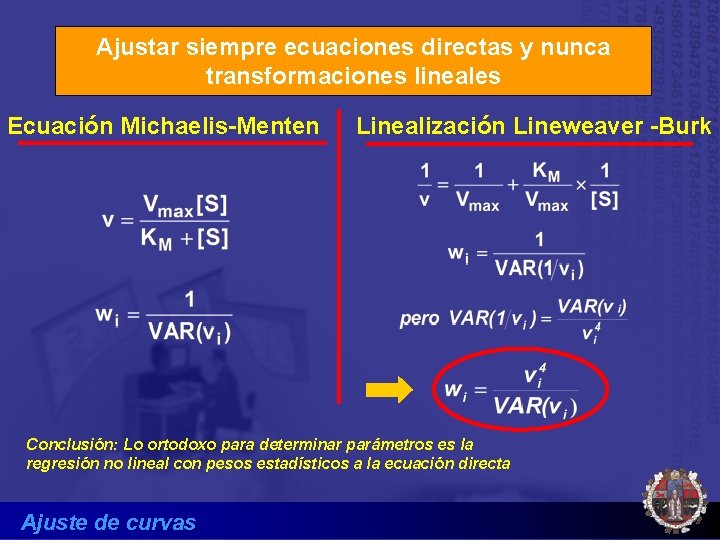
Ajustar siempre ecuaciones directas y nunca transformaciones lineales Ecuación Michaelis-Menten Linealización Lineweaver -Burk Conclusión: Lo ortodoxo para determinar parámetros es la regresión no lineal con pesos estadísticos a la ecuación directa Ajuste de curvas

Ejemplo de regresión no lineal con SIMFIT Con una preparación enzimática de dos isoenzimas se realizó el siguiente estudio: 8 puntos experimentales, en el margen de concentraciones de 0. 05 a 50 m. M, espaciados logarítmicamente y realizándose 5 réplicas por punto (40 datos en total). [S] v s 0. 050 0. 0530 0. 0006 0. 050 0. 0531 0. 0006 0. 050 0. 0523 0. 0006 0. 050 0. 0522 0. 0006 0. 050 0. 0520 0. 0006 …. . 50. 0 1. 73 0. 06 50. 0 1. 86 0. 06 50. 0 1. 77 0. 06 50. 0 1. 76 0. 06 Ajuste de curvas ¿Tienen las 2 isoenzimas la misma Vmax y Km?

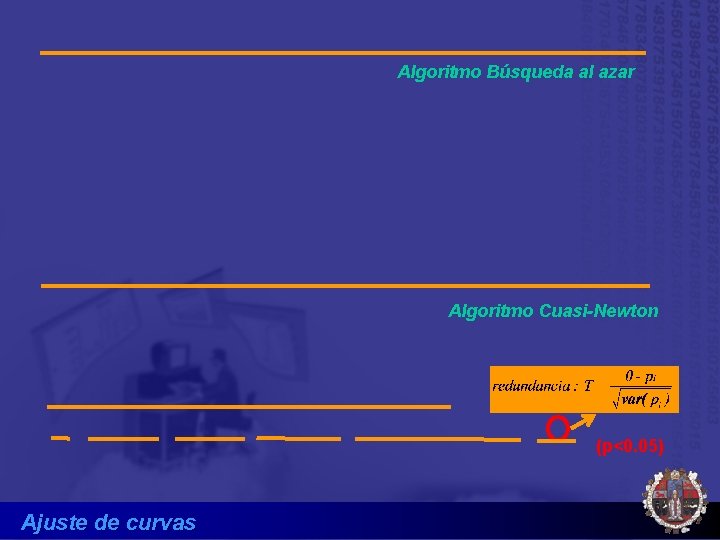
Algoritmo Búsqueda al azar Algoritmo Cuasi-Newton (p<0. 05) Ajuste de curvas

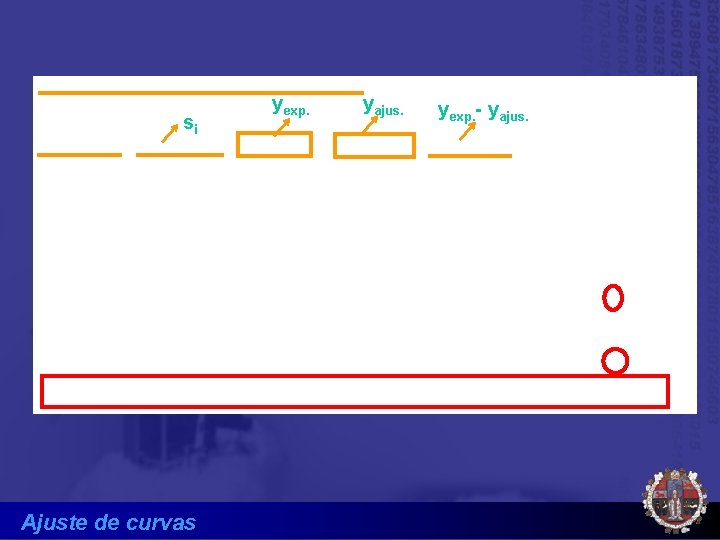
si Ajuste de curvas yexp. yajus. yexp. - yajus.

Tabla de análisis global de los residuales (importante) weighted sum of squares Test c 2 (p < 0. 01) Test rachas (p < 0. 01) cualitativo (poco valor) Ajuste de curvas

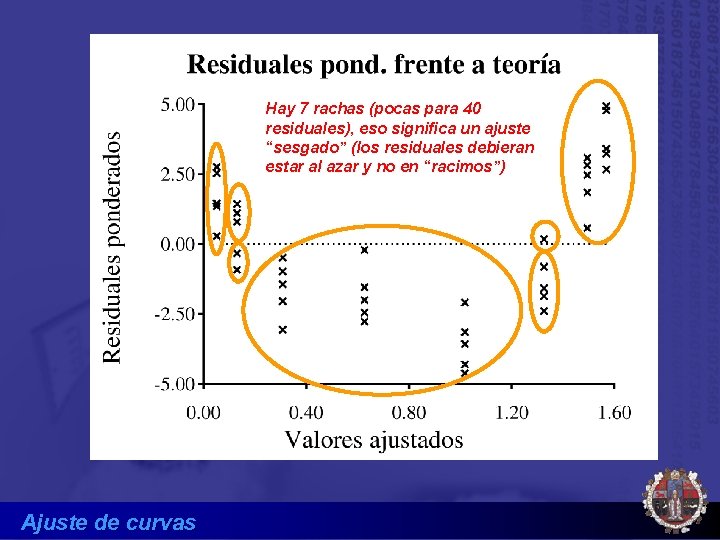
Hay 7 rachas (pocas para 40 residuales), eso significa un ajuste “sesgado” (los residuales debieran estar al azar y no en “racimos”) Ajuste de curvas

Ajuste de curvas

Entra automáticamente el ajuste a 2 Michaelis-Menten Algoritmo búsqueda al azar Algoritmo Cuasi-Newton Las 4 “p” son < 0. 05 , parámetros distintos “ 0” Ajuste de curvas

Residuales Ajuste de curvas

Análisis global de los residuales para 2 Michaelis-Menten (disminuyó (antes 2. 43 E+02)) Test c 2 (buen ajuste p > 0. 05) (disminuyó (antes 5. 66 %)) (aumentó (antes 7 )) (test rachas (buen ajuste ( p > 0. 05 )) Ajuste de curvas

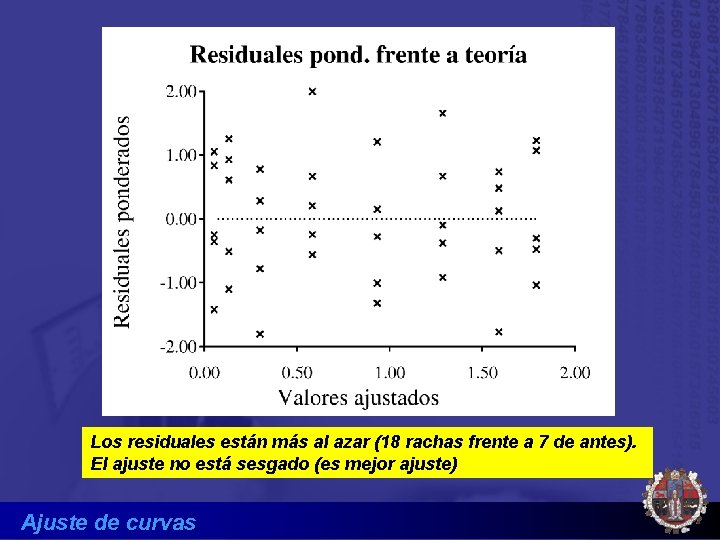
Los residuales están más al azar (18 rachas frente a 7 de antes). El ajuste no está sesgado (es mejor ajuste) Ajuste de curvas

Ajuste de curvas

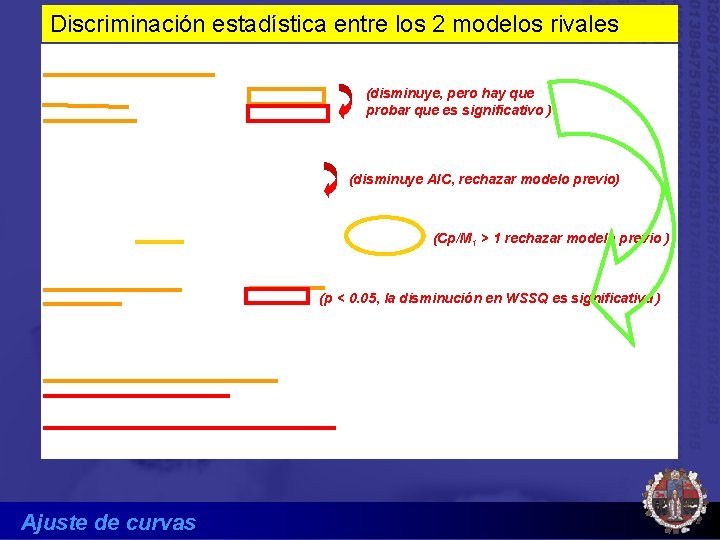
Discriminación estadística entre los 2 modelos rivales (disminuye, pero hay que probar que es significativo ) (disminuye AIC, rechazar modelo previo) (Cp/M 1 > 1 rechazar modelo previo ) (p < 0. 05, la disminución en WSSQ es significativa ) Ajuste de curvas

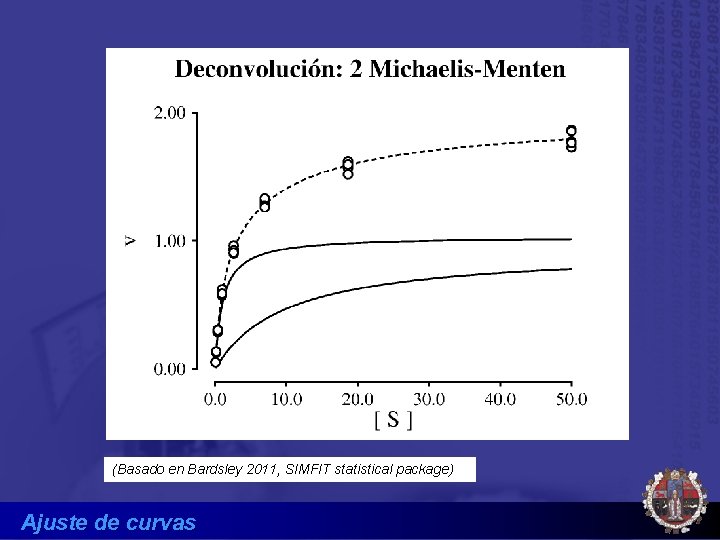
(Basado en Bardsley 2011, SIMFIT statistical package) Ajuste de curvas

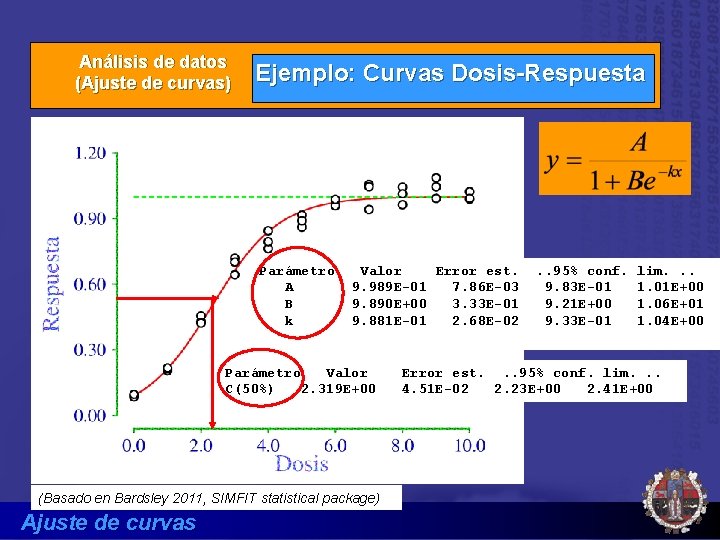
Análisis de datos (Ajuste de curvas) Ejemplo: Curvas Dosis-Respuesta Parámetro A B k Valor Error est. 9. 989 E-01 7. 86 E-03 9. 890 E+00 3. 33 E-01 9. 881 E-01 2. 68 E-02 Parámetro Valor C(50%) 2. 319 E+00 (Basado en Bardsley 2011, SIMFIT statistical package) Ajuste de curvas . . 95% conf. 9. 83 E-01 9. 21 E+00 9. 33 E-01 lim. . . 1. 01 E+00 1. 06 E+01 1. 04 E+00 Error est. . . 95% conf. lim. . . 4. 51 E-02 2. 23 E+00 2. 41 E+00

Diferencia entre curvas de 2 tratamientos Ojo: aquí A y B significan los tratamientos Test Mahalanobis Ji-cuadrado =========================== Q = (A-B)^T(Ca+Cb)^(-1)(A-B) = 2. 806 E+03 Nº grados de libertad = 3 Prob. (Ji-cuadr. >= Q) = 0. 0000 Test t entre parámetros para 2 tratamientos(A, B) con covarianzas (Ca, Cb). =========================== Param. A B A - B p 1 (A) 1. 397 E+00 9. 989 E-01 3. 981 E-01 0. 9750 2 (B) 1. 295 E+01 9. 890 E+00 3. 060 E+00 0. 0000 ***** 3 (k) 1. 306 E+00 9. 881 E-01 3. 179 E-01 0. 3781 Ajuste de curvas

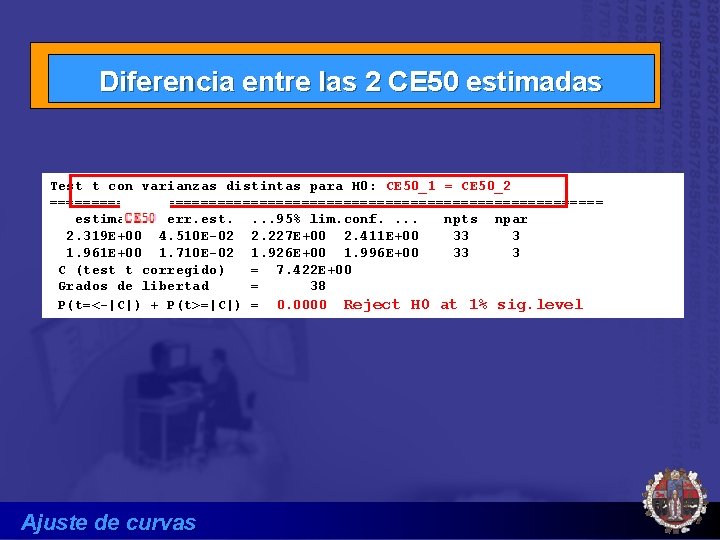
Diferencia entre las 2 CE 50 estimadas Test t con varianzas distintas para H 0: CE 50_1 = CE 50_2 ================================= estimado err. est. . 95% lim. conf. . npts npar 2. 319 E+00 4. 510 E-02 2. 227 E+00 2. 411 E+00 33 3 1. 961 E+00 1. 710 E-02 1. 926 E+00 1. 996 E+00 33 3 C (test t corregido) = 7. 422 E+00 Grados de libertad = 38 P(t=<-|C|) + P(t>=|C|) = 0. 0000 Reject H 0 at 1% sig. level Ajuste de curvas

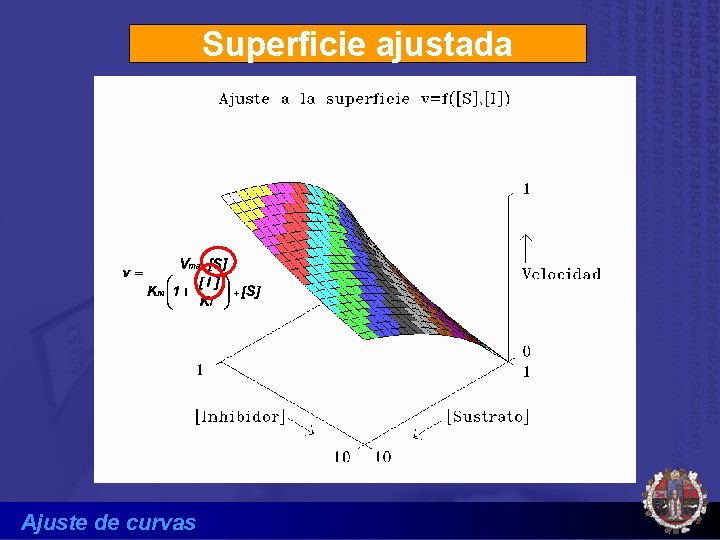
Ajuste a ecuaciones de 2 variables Ecuación: Datos: Inhibidor : 1 1 2 2 Sustrato : 2 4 6 8 2 4 6. 3 7. 1 9. 1 3. 2 5. 2 velocidad : 5. 2 Ajuste de curvas 2 2. . . . 6 8. . . 6. 4 7. 5. . . .

Superficie ajustada Ajuste de curvas

Análisis de datos (Ajuste de curvas) Regr. Lineal generalizada • No es válido el criterio de los mínimos cuadrados. Los ajustes se harán ahora por el método de “máxima verosimilitud”. • Los errores en “y” no siguen una distribución normal sino una distribución binomial, de Poisson etc. • Existe una función predictora de y que es función lineal de las variables independientes estudiadas: • A su vez existe un función de enlace: Ajuste de curvas m

Análisis de datos (Ajuste de curvas) Ajuste de curvas Regr. Lineal generalizada

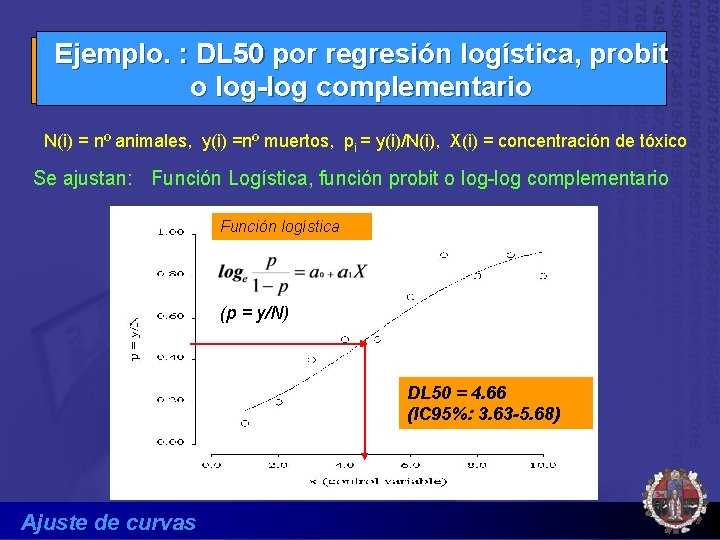
Ejemplo. : DL 50 por regresión logística, probit o log-log complementario N(i) = nº animales, y(i) =nº muertos, pi = y(i)/N(i), X(i) = concentración de tóxico Se ajustan: Función Logística, función probit o log-log complementario Función logística (p = y/N) DL 50 = 4. 66 (IC 95%: 3. 63 -5. 68) Ajuste de curvas

Análisis de datos (Ajuste de curvas) y(i) 1=vivo 0=muerto Ej: Regr. logística binaria variables: X 1 , X 2 , X 3 , . . . p(1) = probabilidad de que y = 1 • La aplicación importante es estimar p(1) para un caso nuevo del que se conocen X 1, , X 2, , X 3, …. (ej: p(1) = 0. 73 de sobrevivir) Ajuste de curvas

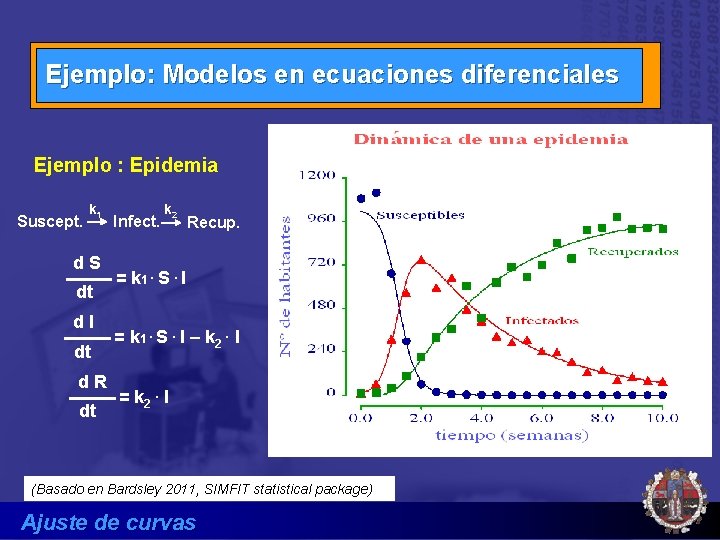
Modelos en ecuaciones diferenciales Ecuaciones diferenciales simultáneas (varias variables dependientes) Ejemplo : Epidemia Susceptibles S dt d. I dt d. R dt k 1 Infectados I k 2 Recuperados R = k 1. S. I – k 2. I = k 2. I Integran numéricamente (Adams, Gear) Ajuste de curvas

Ejemplo: Modelos en ecuaciones diferenciales Ejemplo : Epidemia Suscept. k 1 d. S dt d. I dt d. R dt Infect. k 2 Recup. = k 1. S. I – k 2. I = k 2. I (Basado en Bardsley 2011, SIMFIT statistical package) Ajuste de curvas

Ejemplo de modelos en ecuaciones diferenciales Ejemplo : Epidemia Suscept. k 1 d. S k 1 y k 2 dt d. I Condiciones iniciales: S 0 , I 0 y R 0 Ajuste de curvas dt d. R dt Infect. k 2 Recup. = k 1. S. I – k 2. I = k 2. I

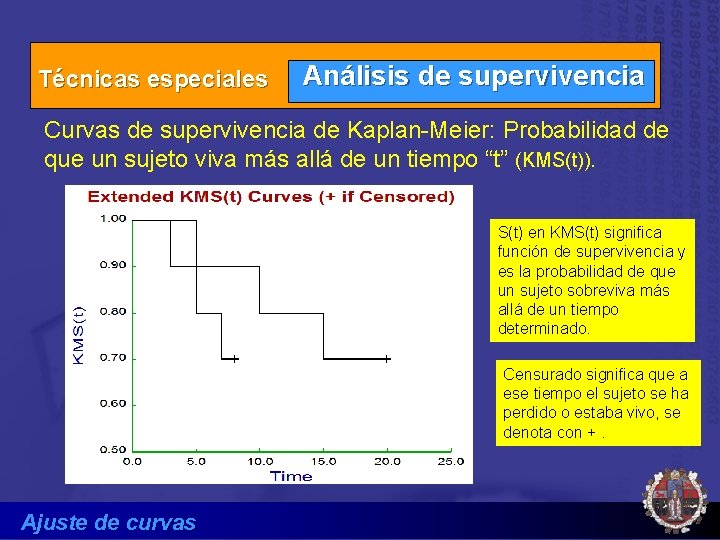
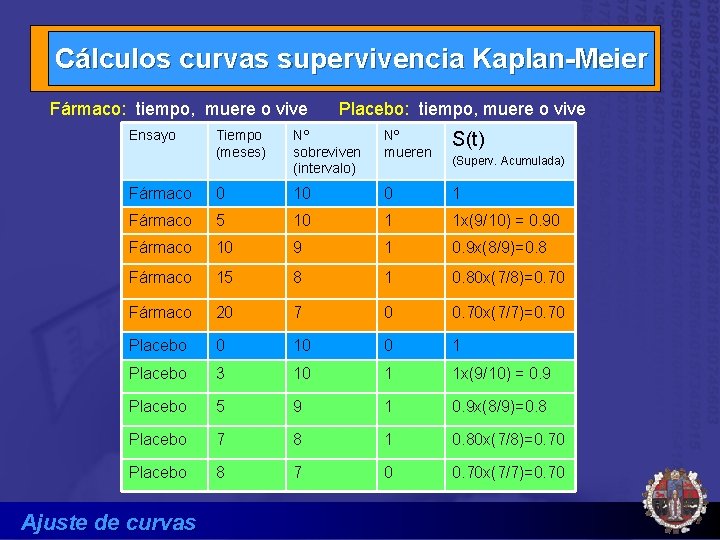
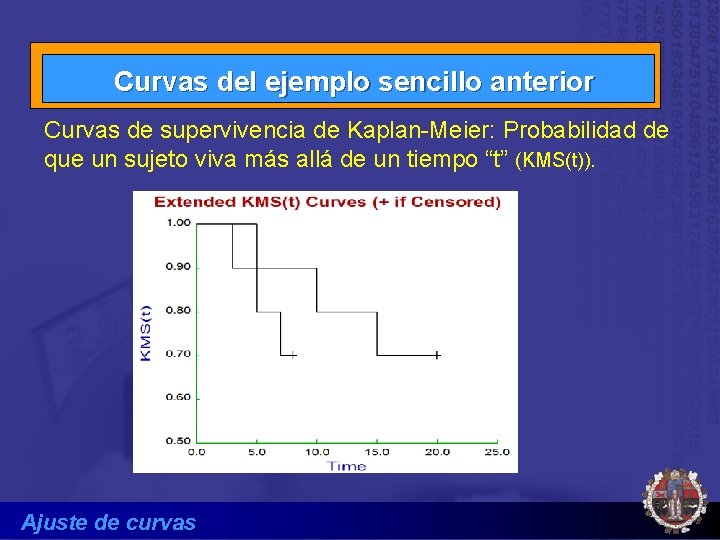
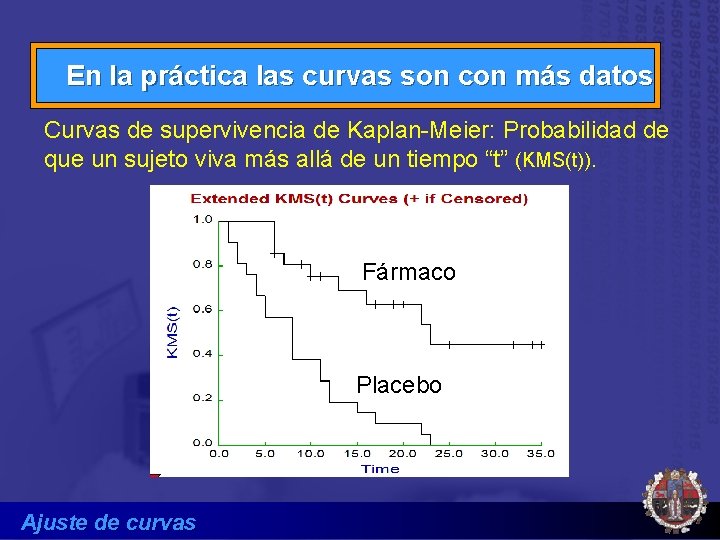
Técnicas especiales Análisis de supervivencia Curvas de supervivencia de Kaplan-Meier: Probabilidad de que un sujeto viva más allá de un tiempo “t” (KMS(t)). S(t) en KMS(t) significa función de supervivencia y es la probabilidad de que un sujeto sobreviva más allá de un tiempo determinado. Censurado significa que a ese tiempo el sujeto se ha perdido o estaba vivo, se denota con +. Ajuste de curvas

Cálculos curvas supervivencia Kaplan-Meier Fármaco: tiempo, muere o vive Ensayo Placebo: tiempo, muere o vive Tiempo (meses) Nº sobreviven (intervalo) Nº mueren S(t) Fármaco 0 10 0 1 Fármaco 5 10 1 1 x(9/10) = 0. 90 Fármaco 10 9 1 0. 9 x(8/9)=0. 8 Fármaco 15 8 1 0. 80 x(7/8)=0. 70 Fármaco 20 7 0 0. 70 x(7/7)=0. 70 Placebo 0 10 0 1 Placebo 3 10 1 1 x(9/10) = 0. 9 Placebo 5 9 1 0. 9 x(8/9)=0. 8 Placebo 7 8 1 0. 80 x(7/8)=0. 70 Placebo 8 7 0 0. 70 x(7/7)=0. 70 Ajuste de curvas (Superv. Acumulada)

Formato curvas Kaplan Meier en SIMFIT Códigos : 0 = muere 1= censurado (perdido o sobrevive) Ajuste de curvas Ensayo Tiempo (meses) Código (0 ó 1) Frecuencia Fármaco 5 0 1 Fármaco 10 0 1 Fármaco 15 0 1 Fármaco 20 1 7 Placebo 3 0 1 Placebo 5 0 1 Placebo 7 0 1 Placebo 8 1 7

Curvas del ejemplo sencillo anterior Curvas de supervivencia de Kaplan-Meier: Probabilidad de que un sujeto viva más allá de un tiempo “t” (KMS(t)). Ajuste de curvas

En la práctica las curvas son con más datos Curvas de supervivencia de Kaplan-Meier: Probabilidad de que un sujeto viva más allá de un tiempo “t” (KMS(t)). Fármaco Placebo Ajuste de curvas

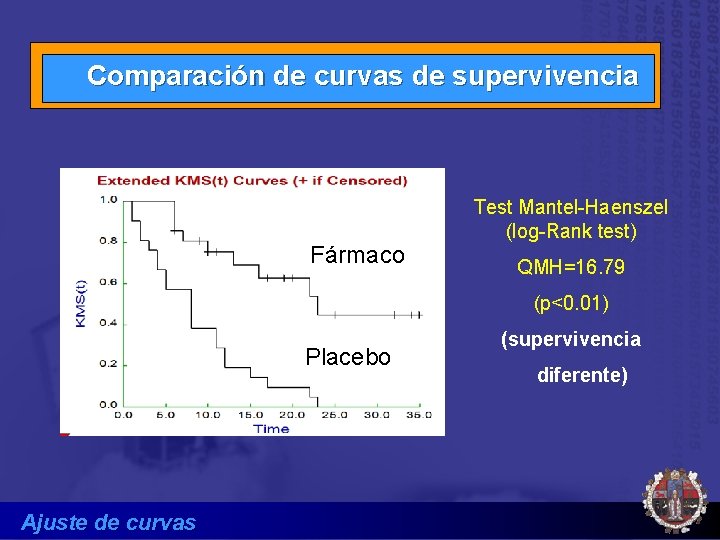
Comparación de curvas de supervivencia Fármaco Test Mantel-Haenszel (log-Rank test) QMH=16. 79 (p<0. 01) Placebo Ajuste de curvas (supervivencia diferente)