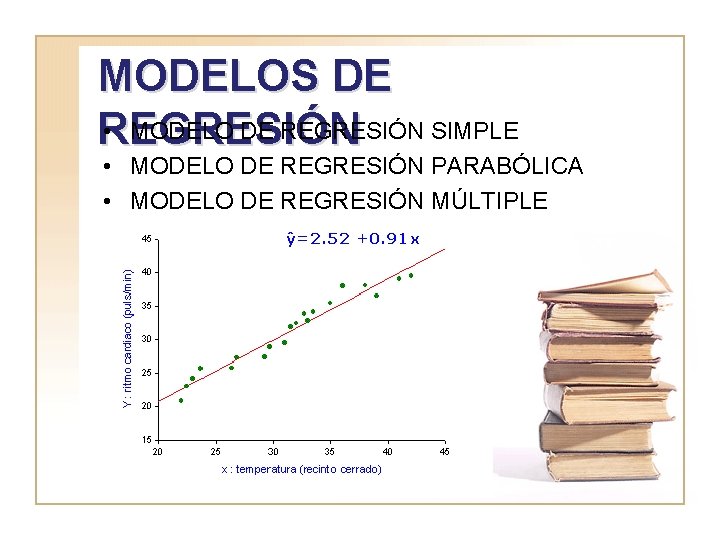
MODELOS DE MODELO DE REGRESIN SIMPLE REGRESIN MODELO

MODELOS DE • MODELO DE REGRESIÓN SIMPLE REGRESIÓN • MODELO DE REGRESIÓN PARABÓLICA • MODELO DE REGRESIÓN MÚLTIPLE

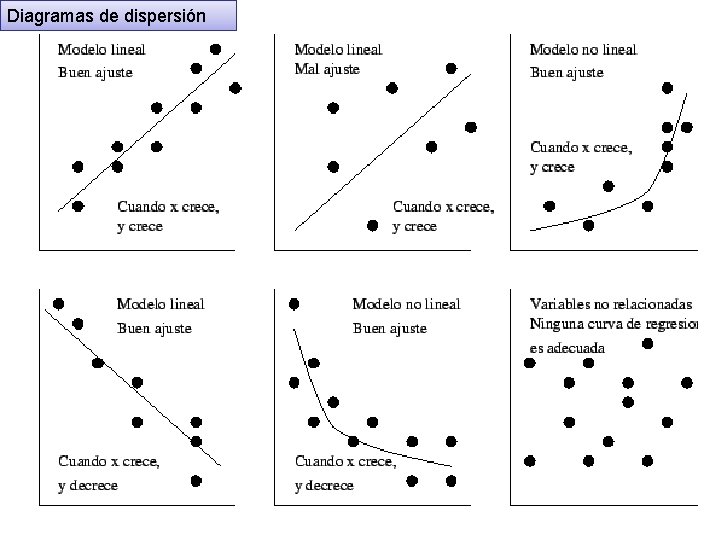
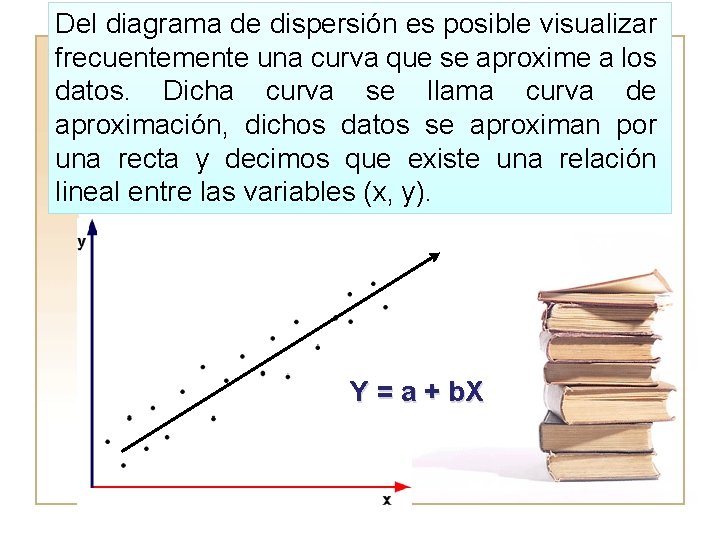
En el análisis de regresión simple se estudia la relación entre 2 variables. Por ejemplo, un caso muy sencillo en economía habla de que las unidades de un producto que se compran (la demanda) dependen del precio al que se ofrezcan (la oferta). El análisis de regresión múltiple maneja una variable dependiente pero existen cuando menos 2 variables independientes. Para evaluar estas relaciones, lo primero que se hace es trazar los valores correspondientes en un plano cartesiano (un plano de ejes vertical y horizontal), conocido como diagrama de dispersión.

Diagramas de dispersión

INTRODUCCIÓN La regresión y la correlación son las dos herramientas más poderosas y versátiles que se pueden utilizar para solucionar problemas comunes en los negocios. Muchos estudios se basan en la creencia de que se pueden identificar y cuantificar alguna relación funcional entre dos o más variables. Se dice que una variable depende de la otra. Se puede decir que Y depende de X en donde Y y X son dos variables cualesquiera. Esto se puede escribir así: Variable independiente = f(X) Y es una función de X Variable dependiente = Y Y = f(X)

Del diagrama de dispersión es posible visualizar frecuentemente una curva que se aproxime a los datos. Dicha curva se llama curva de aproximación, dichos datos se aproximan por una recta y decimos que existe una relación lineal entre las variables (x, y). Y = a + b. X

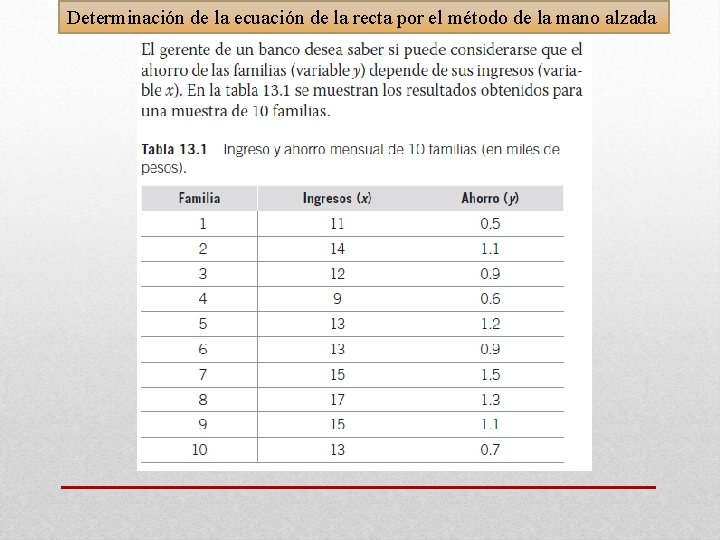
Determinación de la ecuación de la recta por el método de la mano alzada

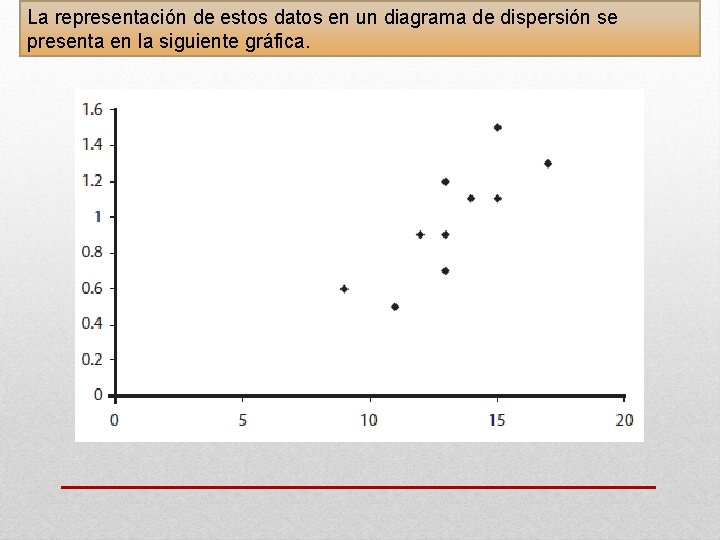
La representación de estos datos en un diagrama de dispersión se presenta en la siguiente gráfica.

Encontrando la ecuación de la recta por el método de la mano alzada. Ecuación de la recta: Y = 0. 10833 x – 0. 54166 Utilizando la ecuación de la recta que se encontró antes, estime la cantidad de ahorro para una familia que tiene ingresos de $10 000 mensuales. Solución: Sustituyendo en la ecuación de regresión : y = 0. 10833 x – 0. 54166 y = 0. 10833(10) – 0. 54166 = 0. 54164 * 1000 = $ 541. 64 de ahorro por mes.

Ejercicio: 1. -) Encuentre la ecuación de la siguiente recta a partir de las coordenadas de los 2 puntos proporcionados: P 1(− 3, − 2) y P 2(4, 5). 2. -) Encuentre la ecuación de la siguiente recta a partir de las coordenadas de los 2 puntos proporcionados: P 1(3, 12) y P 2(8, 2). 3. -) Se tiene una muestra de 8 estudiantes con 2 datos para cada uno: el numero de horas que han dedicado al estudio de una asignatura y la calificación obtenida en el examen correspondiente: (38, 7), (36, 7), (42, 9), (25, 3), (27, 4), (32, 6), (48, 9) y (40, 5). a) Dibuje el diagrama de dispersión de estos puntos. b) Trace a mano alzada la recta que mejor se ajuste a los puntos. c) Encuentre la ecuación de esa recta. d) Estime la calificación que podría obtener un alumno que estudia 30 horas.

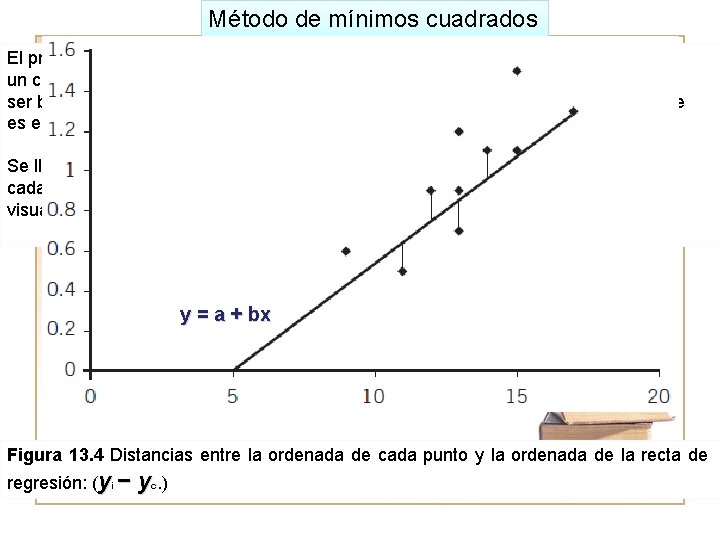
Método de mínimos cuadrados. Para determinar la recta de regresión

Método de mínimos cuadrados El procedimiento manual que se explico antes para ajustar una recta de regresión a un conjunto de datos trazados en un diagrama de dispersión, tiene la desventaja de ser bastante inexacto. El método que comúnmente se utiliza para realizar este ajuste es el llamado método de mínimos cuadrados. Se llama así porque reduce al mínimo el cuadrado de las distancias verticales entre cada uno de los puntos y la recta ajustada. La idea se aprecia visualmente en la figura 13. 4. y = a + bx Figura 13. 4 Distancias entre la ordenada de cada punto y la ordenada de la recta de regresión: (yi − yc. )

Ecuaciones normales simultáneamente permiten construir la ecuación lineal de mínimos cuadrados son: Despejando a y b de las ecuaciones obtenemos lo siguiente:

Método sumas de cuadrados b= SCxy SCxx

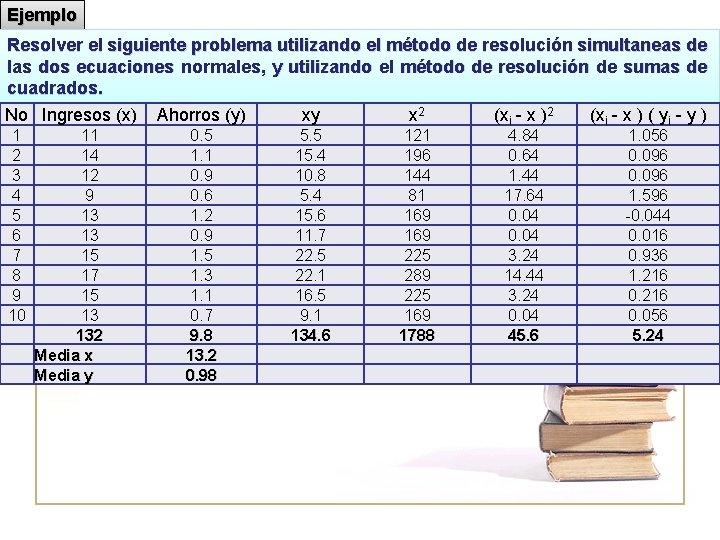
Ejemplo Resolver el siguiente problema utilizando el método de resolución simultaneas de las dos ecuaciones normales, y utilizando el método de resolución de sumas de cuadrados. No Ingresos (x) Ahorros (y) xy x 2 (xi - x ) ( yi - y ) 1 2 3 4 5 6 7 8 9 10 11 14 12 9 13 13 15 17 15 13 132 Media x Media y 0. 5 1. 1 0. 9 0. 6 1. 2 0. 9 1. 5 1. 3 1. 1 0. 7 9. 8 13. 2 0. 98 5. 5 15. 4 10. 8 5. 4 15. 6 11. 7 22. 5 22. 1 16. 5 9. 1 134. 6 121 196 144 81 169 225 289 225 169 1788 4. 84 0. 64 1. 44 17. 64 0. 04 3. 24 14. 44 3. 24 0. 04 45. 6 1. 056 0. 096 1. 596 -0. 044 0. 016 0. 936 1. 216 0. 056 5. 24

Solución por Ecuaciones:

Solución por sustitución:

Solución por método sumas de cuadrados y x= 13. 2 Ecuación de la recta de regresión:

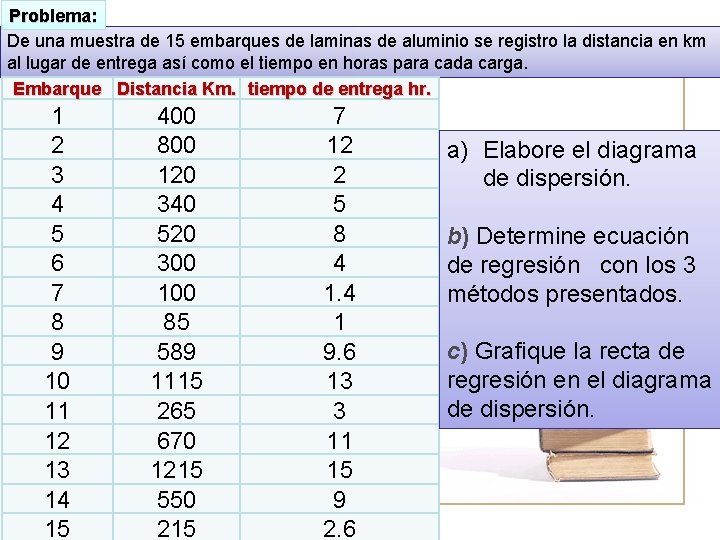
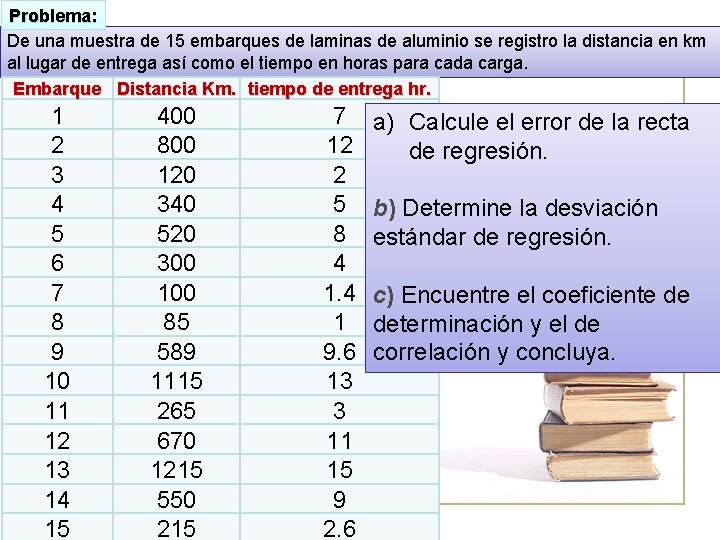
Problema: De una muestra de 15 embarques de laminas de aluminio se registro la distancia en km al lugar de entrega así como el tiempo en horas para cada carga. Embarque Distancia Km. tiempo de entrega hr. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 400 800 120 340 520 300 100 85 589 1115 265 670 1215 550 215 7 12 2 5 8 4 1 9. 6 13 3 11 15 9 2. 6 a) Elabore el diagrama de dispersión. b) Determine ecuación de regresión con los 3 métodos presentados. c) Grafique la recta de regresión en el diagrama de dispersión.

1) Recta de regresión 2) cálculo del error 3) Desviación total 4) Desviación del error 5) Desviación de regresión 6) Suma de cuadrados total 7) Suma de cuadrados del error 8) Suma de cuadrados de regresión 9) Desviación estándar de regresión 10)Coeficiente de determinación 11)Coeficiente de correlación

Recta de regresión y cálculo del error No. 1 2 3 4 5 6 7 8 9 10 Ingresos (x) 11 14 12 9 13 13 15 17 15 13 Ahorros (y) 0. 5 1. 1 0. 9 0. 6 1. 2 0. 9 1. 5 1. 3 1. 1 0. 7 Ŷ = -0. 5367 + 0. 1149(11) = 0. 7272 Ŷ = -0. 5367 + 0. 1149(14) = 1. 0719 Ԑ = ( 0. 5 – 0. 7272)= - 0. 2272 Ԑ = ( 1. 1 – 1. 0719)= 0. 0281 ŷ = - 0. 5367 + 0. 1149 x 0. 7272 1. 0719 0. 8421 0. 4974 0. 957 1. 1868 1. 4166 1. 1868 0. 957 Suma Ԑ = ( yi - ŷ) -0. 2272 0. 0281 0. 0579 0. 1026 0. 243 -0. 057 0. 3132 -0. 1166 -0. 0868 -0. 257 0. 0002

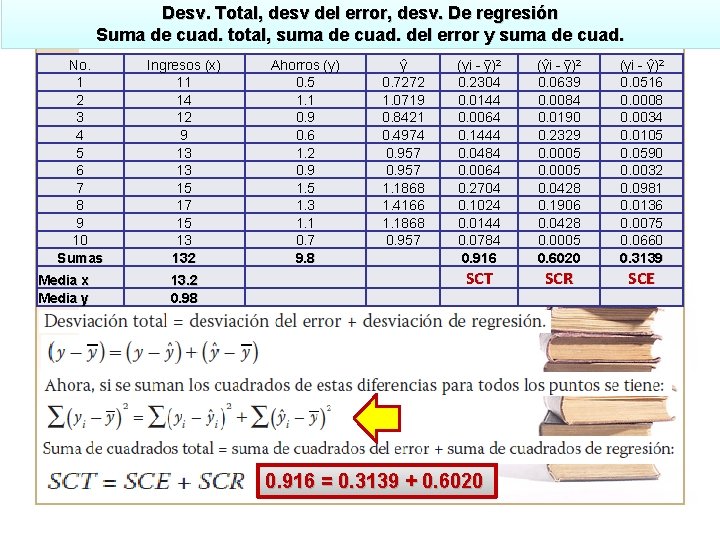
Desv. Total, desv del error, desv. De regresión Suma de cuad. total, suma de cuad. del error y suma de cuad. No. 1 2 3 4 5 6 7 8 9 10 Sumas Media x Media y Ingresos (x) 11 14 12 9 13 13 15 17 15 13 132 13. 2 0. 98 Ahorros (y) 0. 5 1. 1 0. 9 0. 6 1. 2 0. 9 1. 5 1. 3 1. 1 0. 7 9. 8 ŷ 0. 7272 1. 0719 0. 8421 0. 4974 0. 957 1. 1868 1. 4166 1. 1868 0. 957 (yi - ȳ)2 0. 2304 0. 0144 0. 0064 0. 1444 0. 0484 0. 0064 0. 2704 0. 1024 0. 0144 0. 0784 0. 916 (ŷi - ȳ)2 0. 0639 0. 0084 0. 0190 0. 2329 0. 0005 0. 0428 0. 1906 0. 0428 0. 0005 0. 6020 (yi - ŷ)2 0. 0516 0. 0008 0. 0034 0. 0105 0. 0590 0. 0032 0. 0981 0. 0136 0. 0075 0. 0660 0. 3139 SCT SCR SCE 0. 916 = 0. 3139 + 0. 6020

Las relaciones entre las 3 sumas de cuadrados se utilizan para 3 propósitos: 1. Evaluar la adecuación del modelo. 2. Calcular diferentes medidas que se utilizan tanto en el análisis de correlación como en la evaluación de la dispersión de los datos alrededor de la recta de regresión. 3. En los procedimientos que se siguen para hacer pruebas de hipótesis y estimaciones por intervalo de la pendiente de la recta. Desviación estándar de regresión La desviación estándar de regresión es la desviación estándar de los valores y con respecto a los valores ˆy; es representada mediante el símbolo s, y es un estimador del verdadero valor de la población, σ. La formula que resume el procedimiento para calcularla es:

Análisis de correlación El análisis de regresión y el de correlación están estrechamente ligados. Se ha revisado como el análisis de regresión lineal simple se utiliza para calcular la ecuación de una recta que minimiza los cuadrados de las desviaciones (verticales) de cada observación con respecto a la línea ajustada: (y - ŷ)2. También se ha identificado como se utiliza esta ecuación de regresión para estimar y pronosticar otros valores de la variable dependiente, y, para ciertos valores de la variable independiente, x. El análisis de regresión mas sencillo es el que corresponde a: Ø Una relación lineal, es decir, en forma de línea recta, Ø Una relación simple, es decir, una relación entre 2 variables, x y y, la variable independiente y la dependiente, respectivamente. Además del análisis de regresión puede aplicarse el análisis de correlación en el que se revisa, ya no el tipo de relación, sino la intensidad y el sentido de la relación entre las 2 variables. Esta intensidad de la relación suele medirse a través de 2 vías: el coeficiente de determinación que se denota por r 2 y el coeficiente de correlación denotado por r, el cual, tal como puede apreciarse en la simbología, es la raíz cuadrada de r 2, o sea √r 2 = r.

Coeficiente de determinación y correlación Fórmula del coeficiente de determinación: Cuando r 2 se aproxima a uno(1), los valores de “y” están cerca de la línea de regresión, por lo tanto, la variación total de los valores es mas explicada por la línea, así la variable “y” esta estrechamente relacionada con la variable “x”. Cuando la r 2 se aproxima a cero(0), los valores de “y” están lejos de la recta de regresión y la variable “y” no esta estrechamente relacionada con la variable x. Fórmula del coeficiente de correlación: Los valores de la correlación van en el rango de , − 1 ≤ r ≤ 1, en donde el signo + indica una correlación positiva, en tanto que – indica una correlación negativa.

Problema: De una muestra de 15 embarques de laminas de aluminio se registro la distancia en km al lugar de entrega así como el tiempo en horas para cada carga. Embarque Distancia Km. tiempo de entrega hr. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 400 800 120 340 520 300 100 85 589 1115 265 670 1215 550 215 7 12 2 5 8 4 1 9. 6 13 3 11 15 9 2. 6 a) Calcule el error de la recta de regresión. b) Determine la desviación estándar de regresión. c) Encuentre el coeficiente de determinación y el de correlación y concluya.

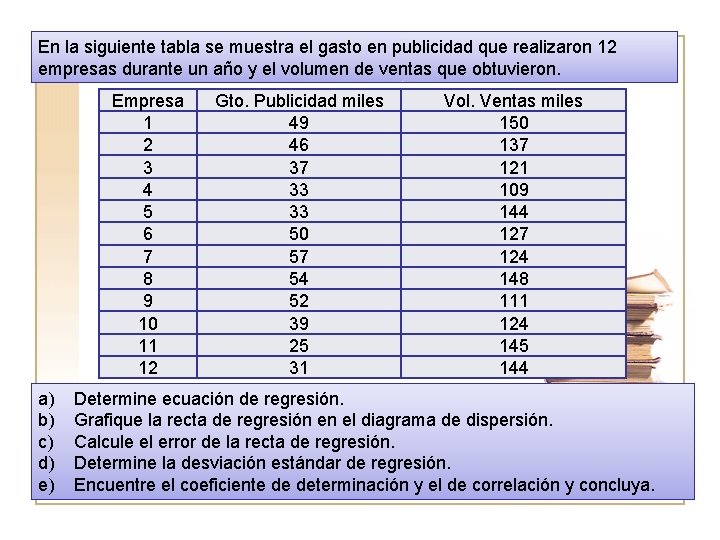
En la siguiente tabla se muestra el gasto en publicidad que realizaron 12 empresas durante un año y el volumen de ventas que obtuvieron. Empresa 1 2 3 4 5 6 7 8 9 10 11 12 a) b) c) d) e) Gto. Publicidad miles 49 46 37 33 33 50 57 54 52 39 25 31 Vol. Ventas miles 150 137 121 109 144 127 124 148 111 124 145 144 Determine ecuación de regresión. Grafique la recta de regresión en el diagrama de dispersión. Calcule el error de la recta de regresión. Determine la desviación estándar de regresión. Encuentre el coeficiente de determinación y el de correlación y concluya.

MODELO DE REGRESIÓN PARABÓLICA

MODELO DE REGRESIÓN PARABÓLICA Curva de ajuste Muy a menudo en la práctica se encuentra que existe una relación entre dos o más variables (x, y), y si se desea expresar esta relación en forma matemática, determinando una ecuación que conecte las variables. Un primer paso es dibujar los puntos (xi, yi) en un sistema de coordenadas rectangulares. El conjunto resultante de puntos se llama diagrama de dispersión.

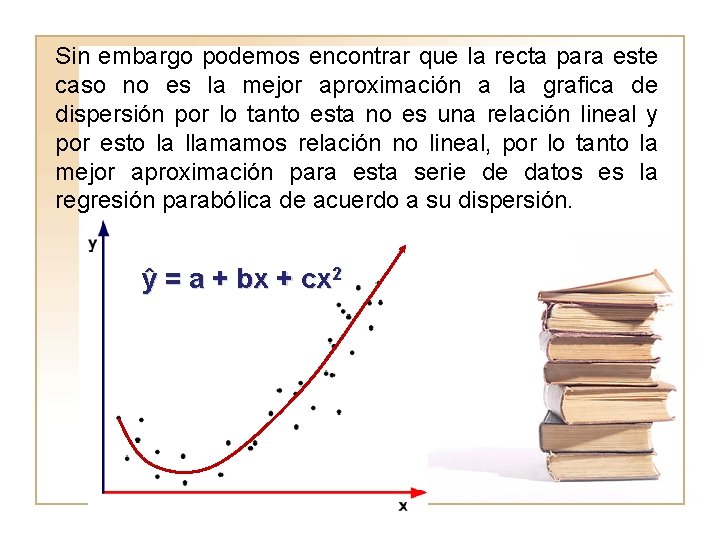
Sin embargo podemos encontrar que la recta para este caso no es la mejor aproximación a la grafica de dispersión por lo tanto esta no es una relación lineal y por esto la llamamos relación no lineal, por lo tanto la mejor aproximación para esta serie de datos es la regresión parabólica de acuerdo a su dispersión. ŷ = a + bx + cx 2

PARÁBOLA DE MINIMOS CUADRADOS La parábola de mínimos cuadrados que ajusta un conjunto de puntos muéstrales viene dada por: ŷ = a + bx + cx 2 Donde a, b, c se determinan de las ecuaciones normales siguientes: • ∑ y = na + b ∑ x + c ∑ x 2 • ∑ xy = a ∑ x + b ∑ x 2 + c ∑ x 3 • ∑ x 2 y = a ∑ x 2 + b ∑ x 3 + c ∑ x 4

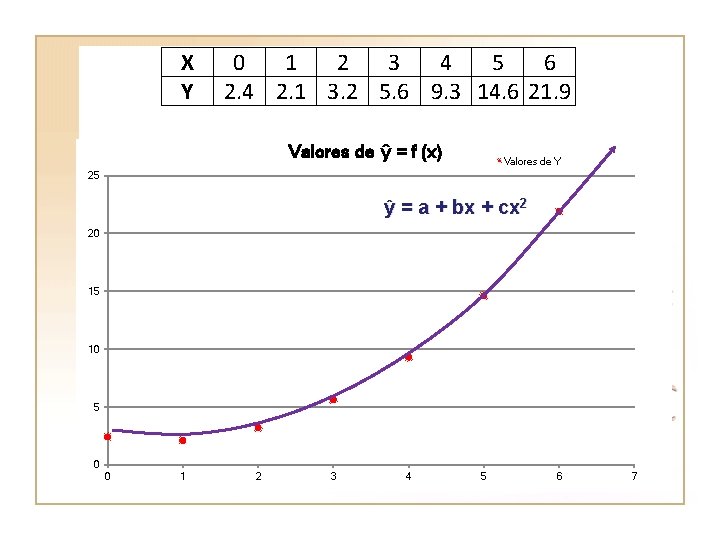
Ejemplo: Ajustar, según convenga, a una recta o una parábola de mínimos cuadrados los datos dados por la siguiente tabla: X 0 1 2 3 4 5 6 Y 2. 4 2. 1 3. 2 5. 6 9. 3 14. 6 21. 9 Determine los valores de Y cuando x = 7, 8, 9 y 10 Solución: El primer paso antes de tratar de ajustar una serie de datos a una fórmula consiste en poner los datos sobre una gráfica para intentar descubrir la tendencia mostrada por los datos. En este caso, la gráfica resulta ser:

X Y 0 1 2 3 4 5 6 2. 4 2. 1 3. 2 5. 6 9. 3 14. 6 21. 9 Valores de ŷ = f (x) Valores de Y 25 ŷ = a + bx + cx 2 20 15 10 5 0 0 1 2 3 4 5 6 7

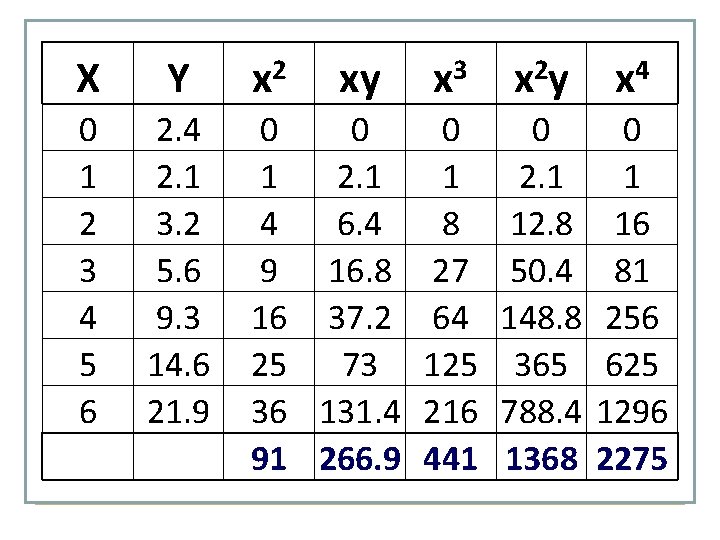
X Y 0 1 2 3 4 5 6 21 2. 4 2. 1 3. 2 5. 6 9. 3 14. 6 21. 9 59. 1 2 x xy 3 x 0 0 0 1 2. 1 1 4 6. 4 8 9 16. 8 27 16 37. 2 64 25 73 125 36 131. 4 216 91 266. 9 441 2 xy 4 x 0 2. 1 12. 8 50. 4 148. 8 365 788. 4 1368 0 1 16 81 256 625 1296 2275

• ∑ y = na + b ∑ x + c ∑ x 2 ∑ y = 59. 1 n=7 • ∑ xy = a ∑ x + b ∑ x 2 + c ∑ x 3 ∑ x = 21 ∑ x 2 = 91 • ∑ x 2 y = a ∑ x 2 + b ∑ x 3 + c ∑ x 4 ∑ xy = 266. 9 ∑ x 3 = 441 ∑ x 2 y = 1, 368 ∑ x 4 = 2, 275 Sustituimos los valores de la tabla en las ecuaciones: 59. 1 = 7 a + 21 b + 91 c 266. 9 = 21 a + 91 b + 441 c 1, 368 = 91 a + 441 b + 2, 275 c

59. 1 = 7 a + 21 b + 91 c 266. 9 = 21 a + 91 b + 441 c 1, 368 = 91 a + 441 b + 2, 275 c a = 2. 539285714 b = - 1. 235714286 c = 0. 739285714 ŷ = a + bx + cx 2 ŷ = 2. 54 – 1. 24 x + 0. 74 x 2

Y = 2. 54 – 1. 24 x + 0. 74 x 2 Y = 2. 54 – 1. 24(7) + 0. 74(7)2 Y = 30. 12 Y = 2. 54 – 1. 24(8) + 0. 74(8)2 Y = 39. 98 Y = 2. 54 – 1. 24(9) + 0. 74(9)2 Y = 51. 32 Y = 2. 54 – 1. 24(10) + 0. 74(10)2 Y = 64. 14 X Y 0 2. 4 1 2 3. 2 3 5. 6 4 5 6 7 8 9 10 9. 3 14. 6 21. 9 30. 1 40 51. 3 64. 1

MODELO DE REGRESIÓN MÚLTIPLE

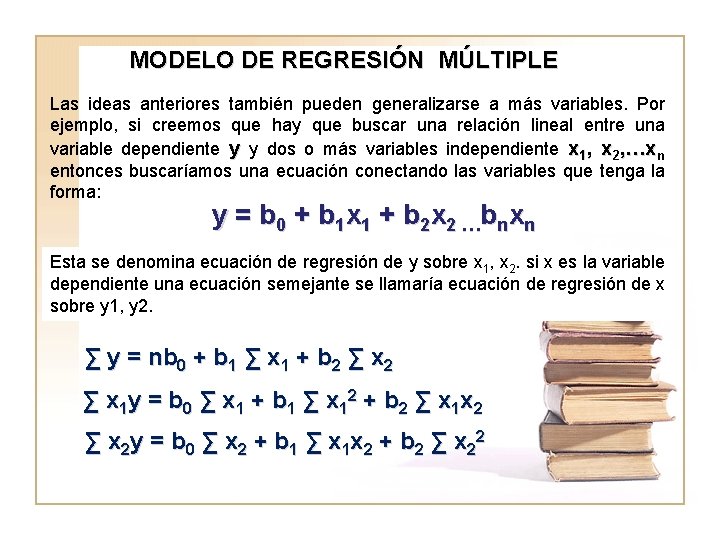
MODELO DE REGRESIÓN MÚLTIPLE Las ideas anteriores también pueden generalizarse a más variables. Por ejemplo, si creemos que hay que buscar una relación lineal entre una variable dependiente y y dos o más variables independiente x 1, x 2, …xn entonces buscaríamos una ecuación conectando las variables que tenga la forma: y = b 0 + b 1 x 1 + b 2 x 2 … b n x n Esta se denomina ecuación de regresión de y sobre x 1, x 2. si x es la variable dependiente una ecuación semejante se llamaría ecuación de regresión de x sobre y 1, y 2. ∑ y = nb 0 + b 1 ∑ x 1 + b 2 ∑ x 1 y = b 0 ∑ x 1 + b 1 ∑ x 12 + b 2 ∑ x 1 x 2 ∑ x 2 y = b 0 ∑ x 2 + b 1 ∑ x 1 x 2 + b 2 ∑ x 22

Coeficiente de determinación, determinación ajustada y coeficiente de correlación múltiple. Este coeficiente de determinación múltiple, r 2, proporciona una medida global de que tan adecuada es la ecuación para medir la relación entre las variables. Este coeficiente de determinación múltiple indica que proporción de la variabilidad total de la variable dependiente seria explicada por las variables independientes. Sin embargo, en este caso, como r 2 es un estimador positivamente sesgado del correspondiente parámetro poblacional, se le ajusta de la siguiente manera: k = No. De variables independientes de la ecuación.

Ejemplo: Peso (y) 64 71 53 67 55 58 77 57 56 51 76 68 Estatura (x 1) 57 59 49 62 51 50 55 48 52 42 61 57 Edad (x 2) 10 6 11 8 7 10 9 10 6 12 9 8 Determinar el peso cuando x 1 = 45, 55 y 65 x 2 = 7, 9, y 11 y = b 0 + b 1 x 1 + b 2 x 2 ∑ y = nb 0 + b 1 ∑ x 1 + b 2 ∑ x 1 y = b 0 ∑ x 1 + b 1 ∑ x 12 + b 2 ∑ x 1 x 2 ∑ x 2 y = b 0 ∑ x 2 + b 1 ∑ x 1 x 2 + b 2 ∑ x 22

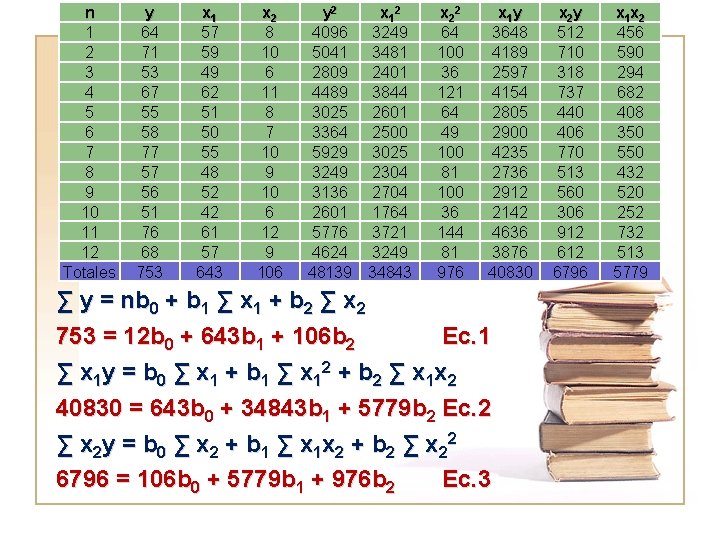
n 1 2 3 4 5 6 7 8 9 10 11 12 Totales y 64 71 53 67 55 58 77 57 56 51 76 68 753 x 1 57 59 49 62 51 50 55 48 52 42 61 57 643 x 2 8 10 6 11 8 7 10 9 10 6 12 9 106 y 2 x 1 2 4096 3249 5041 3481 2809 2401 4489 3844 3025 2601 3364 2500 5929 3025 3249 2304 3136 2704 2601 1764 5776 3721 4624 3249 48139 34843 x 2 2 64 100 36 121 64 49 100 81 100 36 144 81 976 x 1 y 3648 4189 2597 4154 2805 2900 4235 2736 2912 2142 4636 3876 40830 ∑ y = nb 0 + b 1 ∑ x 1 + b 2 ∑ x 2 753 = 12 b 0 + 643 b 1 + 106 b 2 Ec. 1 ∑ x 1 y = b 0 ∑ x 1 + b 1 ∑ x 12 + b 2 ∑ x 1 x 2 40830 = 643 b 0 + 34843 b 1 + 5779 b 2 Ec. 2 ∑ x 2 y = b 0 ∑ x 2 + b 1 ∑ x 1 x 2 + b 2 ∑ x 22 6796 = 106 b 0 + 5779 b 1 + 976 b 2 Ec. 3 x 2 y 512 710 318 737 440 406 770 513 560 306 912 6796 x 1 x 2 456 590 294 682 408 350 550 432 520 252 732 513 5779

753 = 12 b 0 + 643 b 1 + 106 b 2 Ec. 1 40830 = 643 b 0 + 34843 b 1 + 5779 b 2 Ec. 2 6796 = 106 b 0 + 5779 b 1 + 976 b 2 b 0 = 3. 651215805 b 1 = 0. 854609929 b 2 = 1. 50633232 Ec. 3 Determinar el peso cuando x 1 = 45, 55 y 65 x 2 = 7, 9, y 11 ŷ = b 0 + b 1 x 1 + b 2 x 2 ŷ = 3. 65 + 0. 8546 x 1 + 1. 5063 x 2 ŷ = 3. 65 + 0. 8546(45) + 1. 5063(7) ŷ = 52. 677 = 53 ŷ = 64. 243 = 64 ŷ = 75. 809 = 76

Encuentre el coeficiente de determinación, determinación ajustada y el coeficiente de correlación múltiple. n 1 2 3 4 5 6 7 8 9 10 11 12 Totales Media ȳ y 64 71 53 67 55 58 77 57 56 51 76 68 753 62. 75 ŷ 64. 41 69. 13 54. 56 73. 20 59. 29 56. 92 65. 72 58. 23 63. 15 48. 58 73. 86 65. 92 (yi - ȳ)2 1. 56 68. 06 95. 06 18. 06 60. 06 22. 56 203. 06 33. 06 45. 56 138. 06 175. 56 27. 56 888. 25 ŷ = 3. 65 + 0. 8546 x 1 + 1. 5063 x 2 = 629. 35 888. 25 =1 – (0. 35624355) (ŷ - ȳ)2 2. 76 40. 76 67. 02 109. 30 12. 01 33. 94 8. 80 20. 45 0. 16 200. 76 123. 35 10. 04 629. 35 = 0. 708528004 = 0. 643756449 r = 0. 802344346

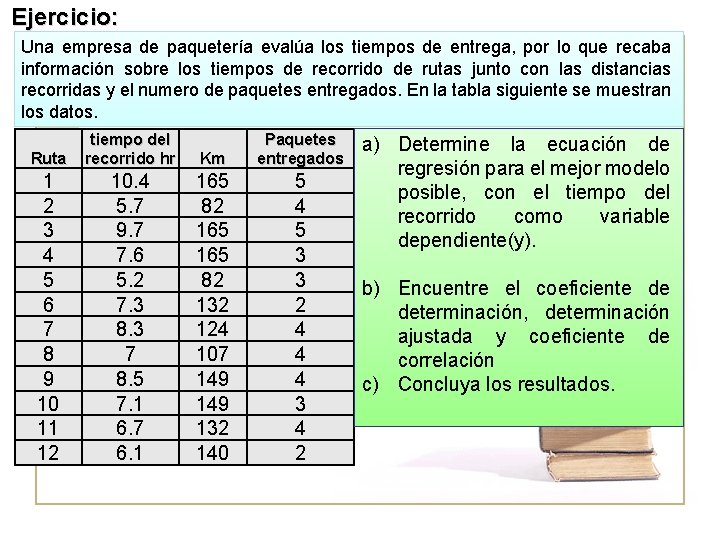
Ejercicio: Una empresa de paquetería evalúa los tiempos de entrega, por lo que recaba información sobre los tiempos de recorrido de rutas junto con las distancias recorridas y el numero de paquetes entregados. En la tabla siguiente se muestran los datos. Ruta tiempo del recorrido hr Km Paquetes entregados 1 2 3 4 5 6 7 8 9 10 11 12 10. 4 5. 7 9. 7 7. 6 5. 2 7. 3 8. 3 7 8. 5 7. 1 6. 7 6. 1 165 82 132 124 107 149 132 140 5 4 5 3 3 2 4 4 4 3 4 2 a) Determine la ecuación de regresión para el mejor modelo posible, con el tiempo del recorrido como variable dependiente(y). b) Encuentre el coeficiente de determinación, determinación ajustada y coeficiente de correlación c) Concluya los resultados.

SERIES DE TIEMPO PRONOSTICOS

Algunos factores tienden a afectar los movimientos de la serie a largo plazo y otros la afectan a corto plazo, de tal manera que todos o algunos de los factores pueden aparecer en una misma serie de tiempo. Existen diferentes métodos para analizar una serie de tiempo, siendo uno de ellos el modelo de descomposición , el cual considera que la serie está compuesta de cuatro patrones básicos: la tendencia (T), las variaciones estacionales (S), las variaciones cíclicas (C) y las variaciones irregulares o aleatorias (I). Por lo tanto, la variable observada (Y) debe estar en función de T, S, C, I. 1. Tendencia (T). 2. Variaciones estacionales (S). 3. Variaciones cíclicas (C). 4. Variaciones aleatorias o irregulares (I).

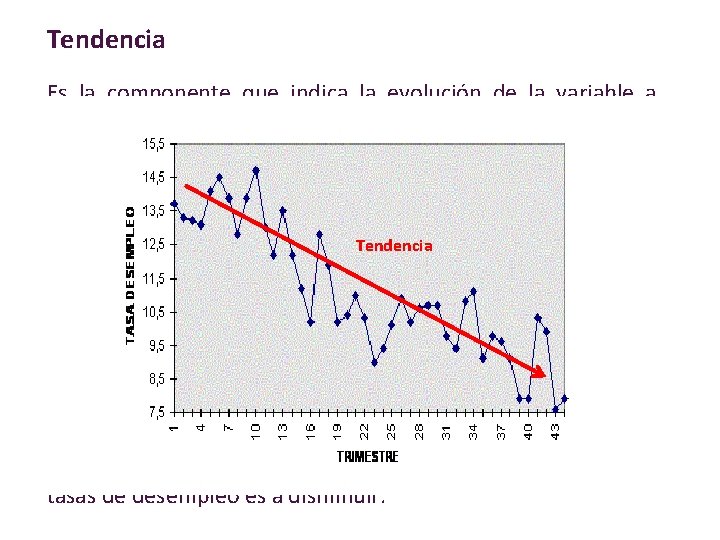
Tendencia Es la componente que indica la evolución de la variable a través del tiempo, evolución que se va a medir como un crecimiento o descenso constante en un período de tiempo prolongado. El período de observación Tendencia de la variable ha de ser suficientemente largo como para incluir dos o más ciclos económicos y así poder tener una idea sobre la evolución real de la variable. Lo que mide la tendencia es la variación promedio de la variable por unidad de tiempo. Esta tendencia se suele describir mediante una recta o algún tipo de curva lisa. En la figura se puede observar que a pesar de tener altibajos durante todo el período de observación, la tendencia (T) de las tasas de desempleo es a disminuir.

Variaciones Estacionales Corresponde a los movimientos en una serie de tiempo, que ocurren año tras año en los mismos meses o períodos del año poco más o menos con la misma intensidad. También se aplica la variación estacional a otros movimientos periódicos por naturaleza, como los que ocurren en un día, una semana o un mes, cuyo período es como máximo un año. Entre los factores más importantes que originan variaciones estacionales, se encuentran las condiciones climáticas, las costumbres sociales y las fiestas religiosas. Las climáticas son la causa más importante de las variaciones estacionales en la producción agrícola, la construcción y el turismo.

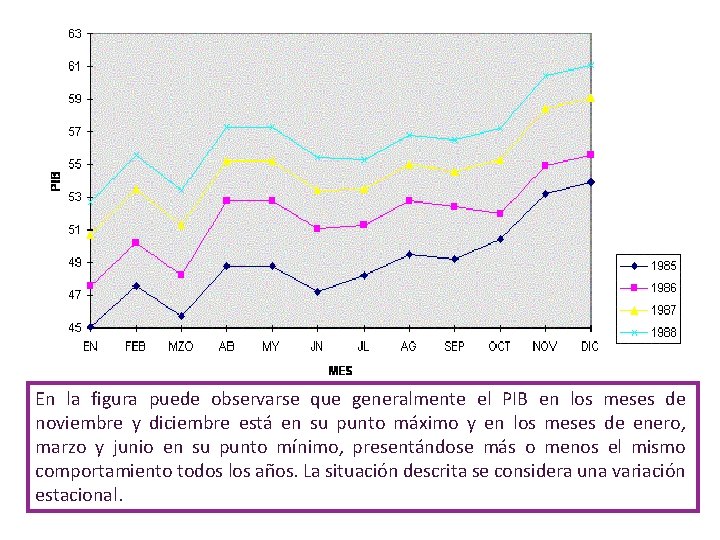
En la figura puede observarse que generalmente el PIB en los meses de noviembre y diciembre está en su punto máximo y en los meses de enero, marzo y junio en su punto mínimo, presentándose más o menos el mismo comportamiento todos los años. La situación descrita se considera una variación estacional.

Variaciones Cíclicas Son los movimientos ascendentes y descendentes de la variable, los cuales difieren de las variaciones estacionales en que se extienden por períodos de tiempo más o menos largos (2 o más años) y, supuestamente, resultan de un conjunto de causas totalmente diferentes que en general son de naturaleza económica y reflejan el estado de las actividades comerciales de tiempo en tiempo. Los períodos recurrentes de expansión, cúspide, contracción y sima constituyen las 4 fases de un ciclo y se consideran causados por factores diferentes del clima y las costumbres sociales que contribuyen a las variaciones estacionales. La principal diferencia entre las variaciones cíclicas y las estacionales es que en las estacionales la periodicidad es de un año como máximo, mientras que en las cíclicas esta periodicidad es mayor; por esta razón para detectar las variaciones cíclicas se debe tener una serie suficientemente larga.

Variaciones aleatorias o irregulares Se deben a razones aleatorias o esporádicas y por lo tanto impredecibles. No obstante, estos sucesos se pueden reconocer e identificar fácilmente. Las variaciones aleatorias son de dos clases: a) Variaciones provocadas por acontecimientos especiales, como elecciones, guerras, inundaciones, terremotos, huelgas, etc. b) Variaciones aleatorias o por casualidad, cuyas causas no se pueden señalar en forma exacta. Las variaciones aleatorias a menudo son poco importantes y se suelen considerar como parte de las estacionales o cíclicas o simplemente se las ignora.

MODELOS SERIE DE TIEMPO 1) MODELO DE PROMEDIOS SIMPLES 2) MODELO DE PROMEDIOS MÓVILES 3) MODELO DE PROMEDIO MÓVIL PONDERADO 4) MODELO DE SUAVIZAMIENTO EXPONENCIAL 5) MODELO PARA DATOS DESESTACIONALIZADOS

Fórmulas de medición del error en el pronóstico www. auladeeconomia. com

Fórmulas de medición del error en el pronóstico

Fórmulas de medición del error en el pronóstico

MODELO PROMEDIO SIMPLE Se obtiene de la media o promedio de todos los valores anteriores, la cual se emplea para pronosticar el periodo siguiente y así sucesivamente.

MODELO PROMEDIO MÓVIL • Este método no considera la media de todos los datos, sino solo los más recientes. • Se puede calcular un promedio móvil de “n” periodos. • El promedio móvil es la media aritmética de los “n” periodos más recientes.

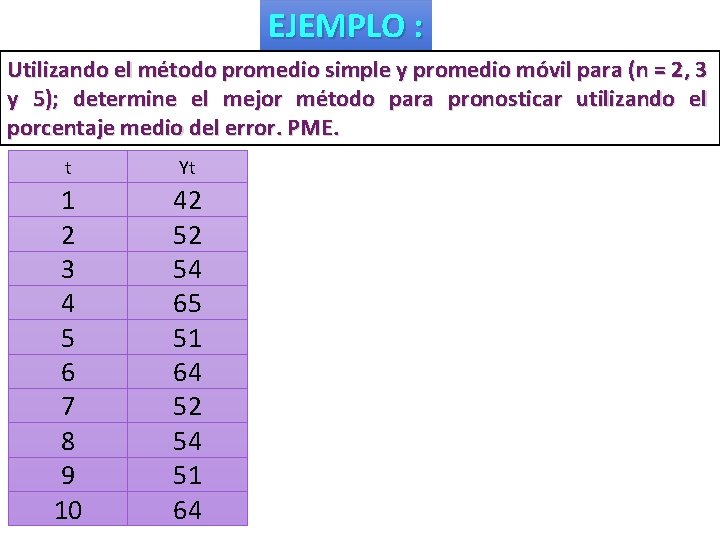
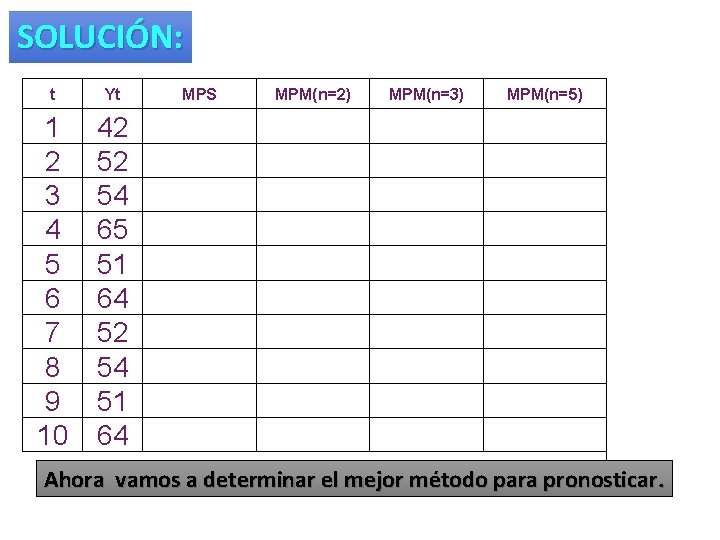
EJEMPLO : Utilizando el método promedio simple y promedio móvil para (n = 2, 3 y 5); determine el mejor método para pronosticar utilizando el porcentaje medio del error. PME. t Yt 1 2 3 4 5 6 7 8 9 10 42 52 54 65 51 64 52 54 51 64

SOLUCIÓN: t Yt MPS MPM(n=2) MPM(n=3) MPM(n=5) 1 2 3 4 5 6 7 8 9 10 42 52 54 65 51 64 52 54 51 64 42. 00 47. 00 49. 33 53. 25 52. 80 54. 67 54. 29 54. 25 53. 89 47. 00 53. 00 59. 50 58. 00 57. 50 58. 00 53. 00 52. 50 49. 33 57. 00 56. 67 60. 00 55. 67 56. 67 52. 33 52. 80 57. 20 54. 40 Ahora vamos a determinar el mejor método para pronosticar.

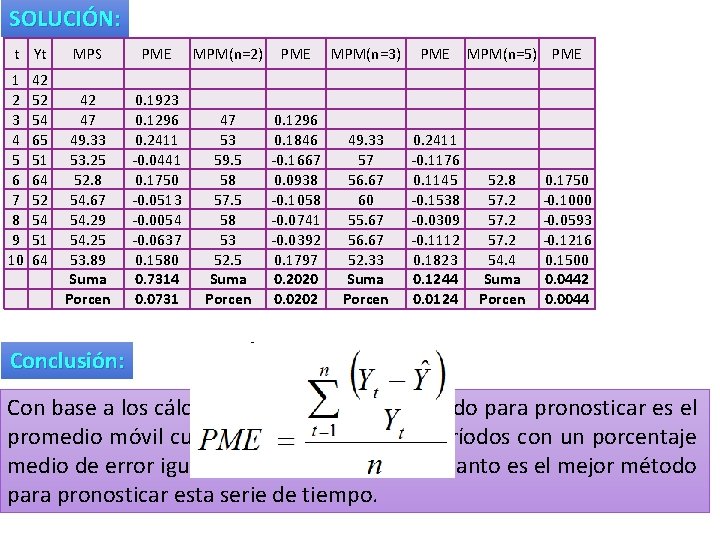
SOLUCIÓN: t Yt 1 2 3 4 5 6 7 8 9 10 42 52 54 65 51 64 52 54 51 64 MPS PME MPM(n=2) PME MPM(n=3) PME 42 47 49. 33 53. 25 52. 8 54. 67 54. 29 54. 25 53. 89 Suma Porcen 0. 1923 0. 1296 0. 2411 -0. 0441 0. 1750 -0. 0513 -0. 0054 -0. 0637 0. 1580 0. 7314 0. 0731 47 53 59. 5 58 57. 5 58 53 52. 5 Suma Porcen 0. 1296 0. 1846 -0. 1667 0. 0938 -0. 1058 -0. 0741 -0. 0392 0. 1797 0. 2020 0. 0202 49. 33 57 56. 67 60 55. 67 56. 67 52. 33 Suma Porcen 0. 2411 -0. 1176 0. 1145 -0. 1538 -0. 0309 -0. 1112 0. 1823 0. 1244 0. 0124 MPM(n=5) PME 52. 8 57. 2 54. 4 Suma Porcen 0. 1750 -0. 1000 -0. 0593 -0. 1216 0. 1500 0. 0442 0. 0044 Conclusión: Con base a los cálculos hechos el mejor método para pronosticar es el promedio móvil cuando n es igual a cinco períodos con un porcentaje medio de error igual a 0. 44 % de error por lo tanto es el mejor método para pronosticar esta serie de tiempo.

Ejercicio: t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 yi 140 131 140 157 119 132 131 148 154 112 157 129 119 139 126 Pronostique la siguiente serie de tiempo diez períodos hacia el futuro, utilizando el método promedio simple y promedio móvil para (n = 2, 3 y 5); calcule para cada método el porcentaje media del error para cada método y concluya cuál es el mejor para pronosticar.

Modelo Promedio móvil ponderado El método consiste en asignar un factor de ponderación distinto para cada dato. Generalmente, a la observación o dato más reciente a partir del que se quiere hacer el pronóstico, se le asigna el mayor peso, y este peso disminuye en los valores de datos más antiguos. Ytn = βYtn-4 + βYtn-3 + βYtn-2 + βYtn-1 Ejemplo: Yt = 0. 4 Yt + 0. 6 Yt Donde la sumatoria del factor (β) debe se igual a 1 Yt = 0. 17 Yt + 0. 33 Yt + 0. 5 Yt Yt = 0. 1 Yt + 0. 2 Yt + 0. 3 Yt + 0. 4 Yt Puede observarse que el dato más alejado tiene el factor de ponderación más pequeño, el siguiente tiene un factor de ponderación mayor que el primero y el dato más reciente tiene un factor de ponderación mayor al anterior. En todos los casos, la suma de los factores de ponderación debe ser igual a uno.

Modelo de suavizamiento exponencial El suavizamiento exponencial emplea un promedio ponderado de la serie de tiempo pasada como pronóstico; es un caso especial del método de promedios móviles ponderados en el cual sólo se selecciona un peso o factor de ponderación: el de la observación más reciente. En la práctica comenzamos haciendo que Y 1, el primer valor de la serie de valores uniformados, sea igual a P 1, que es el primer valor real de la serie. El modelo básico de suavizamiento exponencial es el siguiente: Yt+1 = ⊖Y t + (1 -⊖)Pt Donde: Yt+1 = pronóstico de la serie de tiempo para el período t+1 Yt = valor real de la serie de tiempo en el período t Pt = pronóstico de la serie de tiempo para el período t ⊖ = constante de suavizamiento, 0 ≤⊖ ≤ 1

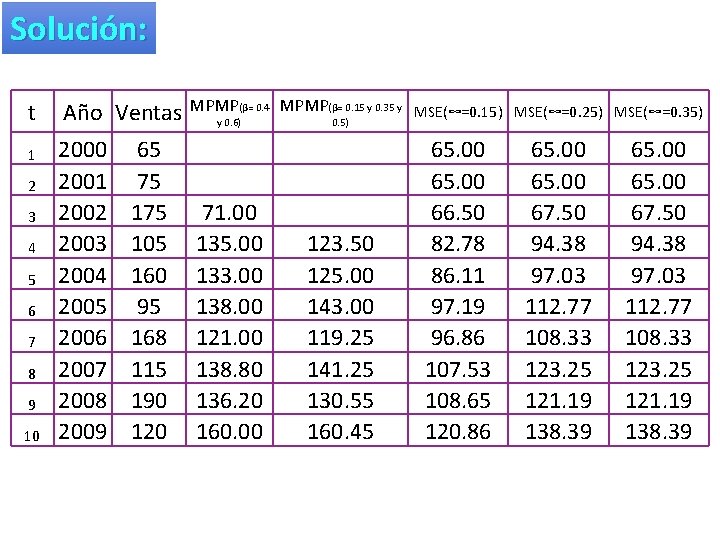
Ejemplo: Con lo datos que a continuación se presentan pronostique utilizando: a. -) Método de promedio móvil ponderado (β =0. 4 y 0. 6 y β = 0. 15, 0. 35 y 0. 5) b. -) suavizamiento exponencial cuando ⊖ = 0. 15 , 0. 25 y 0. 35 Año 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 Ventas 65 75 105 160 95 168 115 190 120

Solución: t 1 2 3 4 5 6 7 8 9 10 (β= 0. 4 Año Ventas MPMP y 0. 6) 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 65 75 105 160 95 168 115 190 120 71. 00 135. 00 133. 00 138. 00 121. 00 138. 80 136. 20 160. 00 MPMP(β= 0. 15 y 0. 35 y MSE(∞=0. 15) MSE(∞=0. 25) MSE(∞=0. 35) 0. 5) 123. 50 125. 00 143. 00 119. 25 141. 25 130. 55 160. 45 65. 00 66. 50 82. 78 86. 11 97. 19 96. 86 107. 53 108. 65 120. 86 65. 00 67. 50 94. 38 97. 03 112. 77 108. 33 123. 25 121. 19 138. 39

Modelo para datos desestacionalizados

Modelo para datos desestacionalizados Los datos muestran alguna tendencia creciente a lo largo del tiempo, además de una marcada estacionalidad Se procederá a desestacionalizar los datos, lo que permite observar hasta donde las variaciones se deben a efectos estacionales o bien, a otros factores

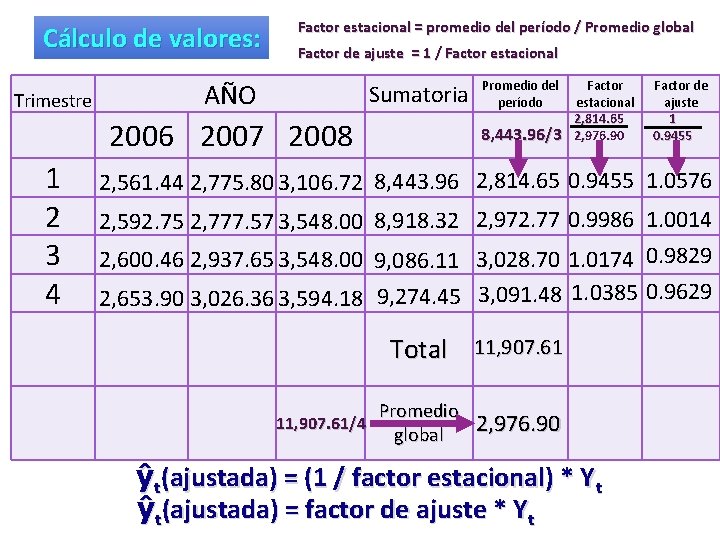
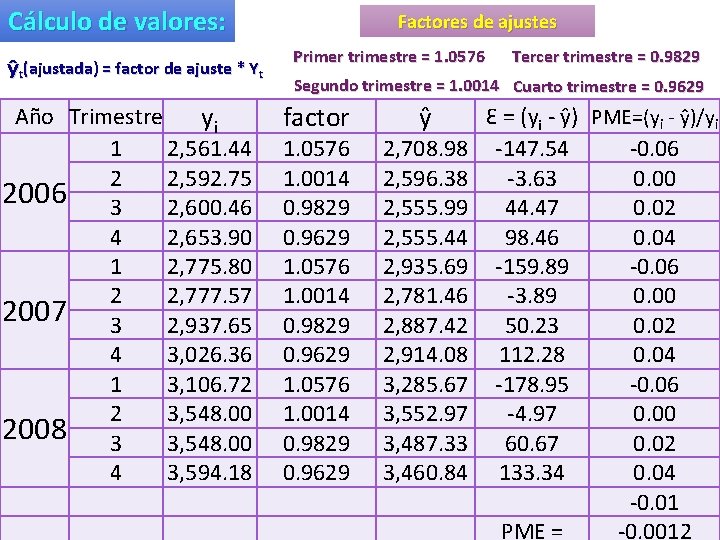
El proceso de ajuste estacional se realizará a través del cálculo de factores estacionales: Factor estacional = promedio del período / Promedio global Factor de ajuste = 1 / Factor estacional ŷt(ajustada) = (1 / factor estacional) * Yt ŷt(ajustada) = factor de ajuste * Yt

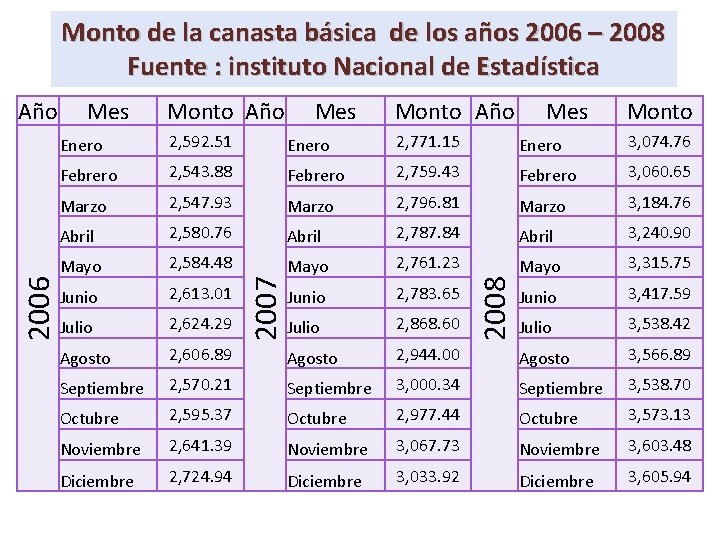
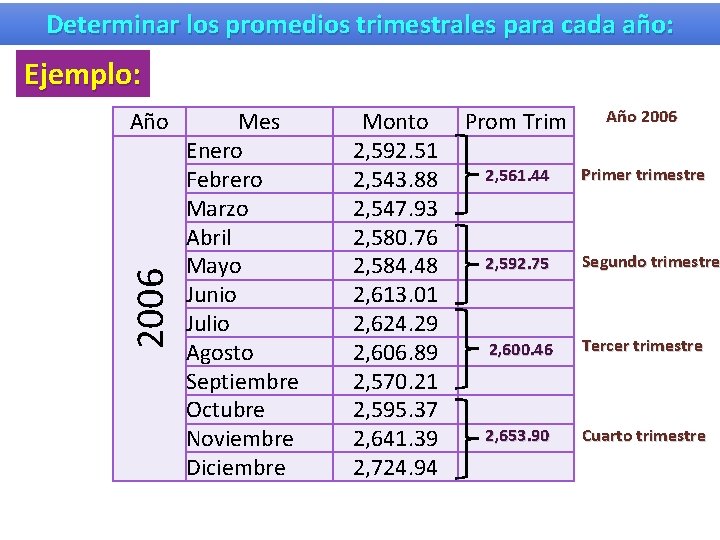
Monto de la canasta básica de los años 2006 – 2008 Fuente : instituto Nacional de Estadística Mes Monto Año Mes Monto 2, 592. 51 Enero 2, 771. 15 Enero 3, 074. 76 Febrero 2, 543. 88 Febrero 2, 759. 43 Febrero 3, 060. 65 Marzo 2, 547. 93 Marzo 2, 796. 81 Marzo 3, 184. 76 Abril 2, 580. 76 Abril 2, 787. 84 Abril 3, 240. 90 Mayo 2, 584. 48 Mayo 2, 761. 23 Mayo 3, 315. 75 Junio 2, 613. 01 Junio 2, 783. 65 Junio 3, 417. 59 Julio 2, 624. 29 Julio 2, 868. 60 Julio 3, 538. 42 Agosto 2, 606. 89 Agosto 2, 944. 00 Agosto 3, 566. 89 Septiembre 2, 570. 21 Septiembre 3, 000. 34 Septiembre 3, 538. 70 Octubre 2, 595. 37 Octubre 2, 977. 44 Octubre 3, 573. 13 Noviembre 2, 641. 39 Noviembre 3, 067. 73 Noviembre 3, 603. 48 Diciembre 2, 724. 94 Diciembre 3, 033. 92 Diciembre 3, 605. 94 2008 Enero 2007 2006 Año

Determinar los promedios trimestrales para cada año: Ejemplo: 2006 Año Mes Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Monto 2, 592. 51 2, 543. 88 2, 547. 93 2, 580. 76 2, 584. 48 2, 613. 01 2, 624. 29 2, 606. 89 2, 570. 21 2, 595. 37 2, 641. 39 2, 724. 94 Prom Trim Año 2006 2, 561. 44 Primer trimestre 2, 592. 75 Segundo trimestre 2, 600. 46 Tercer trimestre 2, 653. 90 Cuarto trimestre

Cálculo de valores: Trimestre Factor estacional = promedio del período / Promedio global Factor de ajuste = 1 / Factor estacional AÑO Sumatoria 2006 2007 2008 1 2 3 4 Promedio del período 8, 443. 96/3 Factor estacional 2, 814. 65 2, 976. 90 Factor de ajuste 1 0. 9455 2, 561. 44 2, 775. 80 3, 106. 72 8, 443. 96 2, 814. 65 0. 9455 1. 0576 2, 592. 75 2, 777. 57 3, 548. 00 8, 918. 32 2, 972. 77 0. 9986 1. 0014 2, 600. 46 2, 937. 65 3, 548. 00 9, 086. 11 3, 028. 70 1. 0174 0. 9829 2, 653. 90 3, 026. 36 3, 594. 18 9, 274. 45 3, 091. 48 1. 0385 0. 9629 11, 907. 61/4 Total 11, 907. 61 Promedio global 2, 976. 90 ŷt(ajustada) = (1 / factor estacional) * Yt ŷt(ajustada) = factor de ajuste * Yt

Cálculo de valores: ŷt(ajustada) = factor de ajuste * Yt Año Trimestre yi 1 2, 561. 44 2 2, 592. 75 2006 3 2, 600. 46 4 2, 653. 90 1 2, 775. 80 2 2, 777. 57 2007 3 2, 937. 65 4 3, 026. 36 1 3, 106. 72 2 3, 548. 00 2008 3 3, 548. 00 4 3, 594. 18 Factores de ajustes Primer trimestre = 1. 0576 Tercer trimestre = 0. 9829 Segundo trimestre = 1. 0014 Cuarto trimestre = 0. 9629 factor ŷ 1. 0576 1. 0014 0. 9829 0. 9629 2, 708. 98 2, 596. 38 2, 555. 99 2, 555. 44 2, 935. 69 2, 781. 46 2, 887. 42 2, 914. 08 3, 285. 67 3, 552. 97 3, 487. 33 3, 460. 84 Ԑ = (yi - ŷ) PME=(yi - ŷ)/yi -147. 54 -0. 06 -3. 63 0. 00 44. 47 0. 02 98. 46 0. 04 -159. 89 -0. 06 -3. 89 0. 00 50. 23 0. 02 112. 28 0. 04 -178. 95 -0. 06 -4. 97 0. 00 60. 67 0. 02 133. 34 0. 04 -0. 01 PME = -0. 0012

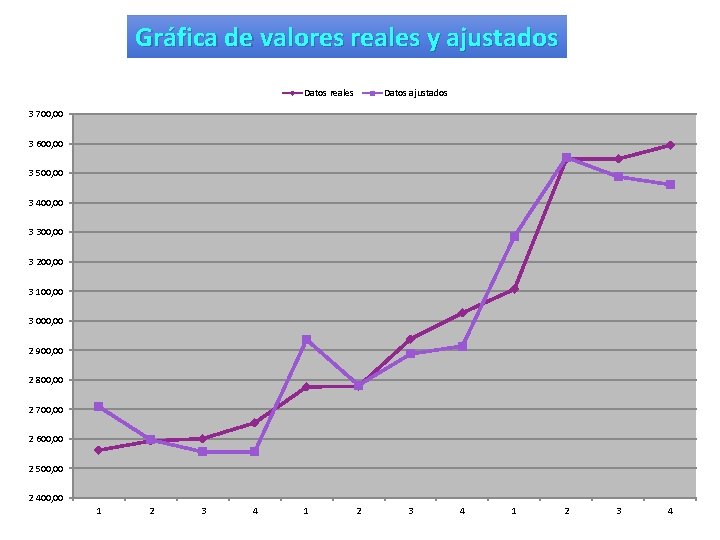
Gráfica de valores reales y ajustados Datos reales Datos ajustados 3 700, 00 3 600, 00 3 500, 00 3 400, 00 3 300, 00 3 200, 00 3 100, 00 3 000, 00 2 900, 00 2 800, 00 2 700, 00 2 600, 00 2 500, 00 2 400, 00 1 2 3 4

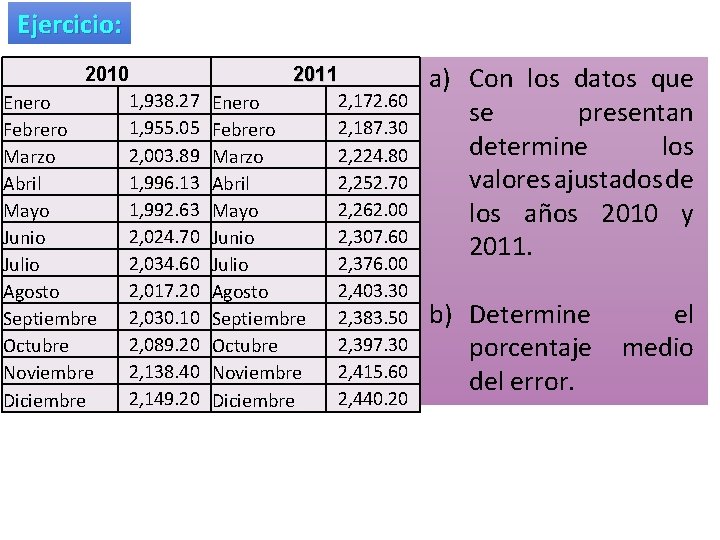
Ejercicio: 2010 1, 938. 27 Enero 1, 955. 05 Febrero 2, 003. 89 Marzo 1, 996. 13 Abril 1, 992. 63 Mayo 2, 024. 70 Junio 2, 034. 60 Julio 2, 017. 20 Agosto 2, 030. 10 Septiembre 2, 089. 20 Octubre 2, 138. 40 Noviembre 2, 149. 20 Diciembre 2011 2, 172. 60 Enero 2, 187. 30 Febrero 2, 224. 80 Marzo 2, 252. 70 Abril 2, 262. 00 Mayo 2, 307. 60 Junio 2, 376. 00 Julio 2, 403. 30 Agosto 2, 383. 50 Septiembre 2, 397. 30 Octubre 2, 415. 60 Noviembre 2, 440. 20 Diciembre a) Con los datos que se presentan determine los valores ajustados de los años 2010 y 2011. b) Determine porcentaje del error. el medio

NÚMEROS ÍNDICES

Definición Números índices son un tipo de medidas estadísticas que estudian los cambios sufridos por una o más variables a través del tiempo. Los números índices se expresan en forma porcentual, siendo el resultado de la misma del valor o de los valores de las variables, divididos entre un valor tomado como base de referencia o comparación, multiplicado por 100, y los cuales están referidos a los precios, cantidades, y valores.

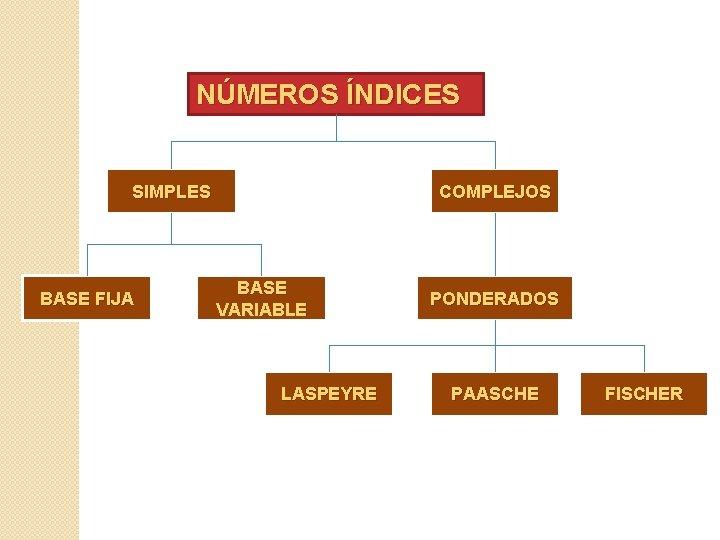
NÚMEROS ÍNDICES SIMPLES BASE FIJA COMPLEJOS BASE VARIABLE LASPEYRE PONDERADOS PAASCHE FISCHER

Índices Simples Cuando nos referimos al Precio cantidad y valor de un solo artículo los cuales están sometidos a variaciones temporales, decimos que nos encontramos ante una serie de números índices simples, los cuales según el período de referencia al cual se lo relaciona se clasifica en índice de base fija e índice de base variable. • Índice de Base Fija. -Es aquel que se mantiene como base de año o período de referencia • Índices de Base Variable. - Son aquellos que tienen como base el año o período anterior al índice de referencia y nos expresa las variaciones existentes de período a período.

Ejemplo Determine el porcentaje de ventas base fija año 1990, base variable, porcentaje de variación año base y base variable. Fórmulas a utilizar: Año 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 Ventas 12 14 18 18 19 20 23 24 26 32 Índice de período base fija Índice de período base variable Pn Pn IPbf = Pbf * 100 IPbv = P n -1 * 100 Porcentaje de variación año base. Porcentaje de variación base variable IPbf = Pn Pbf - 1 * 100 IPbv = Pn - 1 * 100 Pn - 1 IP: Índice período IPbf: período base fija IPbv: período base variable Pn: período actual Pn- 1: período anterior Pbf: período base fija

Ejemplo Año Ventas IP(base 1990) 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 12 14 18 18 19 20 23 24 26 32 100 116. 67 150 158. 33 166. 67 191. 67 200 216. 67 266. 67 18 Porcentaje IP( = base = 1. 5 * 100 = 150% 12 de variación variable) (b 90) (bv) 10018 = 1. 2857 * 100 = 128. 57% = 116. 67 14 128. 57 50 100 0. 00 50 18 105. 56 - 1 *58. 33 = 100 = 0. 50 * 100= 50. 00% 12 105. 26 66. 67 115 15. 00 91. 67 104. 3518 4. 35 100 - 1116. 67 = * 100 = 0. 2857 * 100= 28. 57% 108. 33 14 123. 08 166. 67

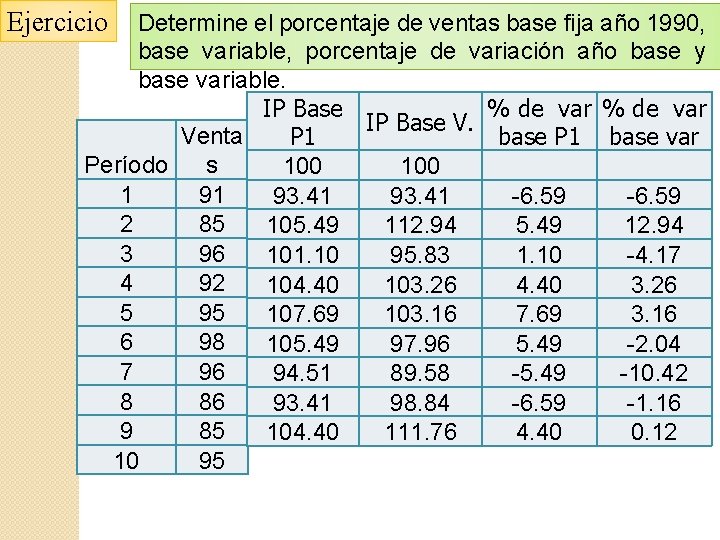
Ejercicio Determine el porcentaje de ventas base fija año 1990, base variable, porcentaje de variación año base y base variable. IP Base % de var IP Base V. Venta P 1 base var Período s 100 1 91 93. 41 -6. 59 2 85 105. 49 112. 94 5. 49 12. 94 3 96 101. 10 95. 83 1. 10 -4. 17 4 92 104. 40 103. 26 4. 40 3. 26 5 95 107. 69 103. 16 7. 69 3. 16 6 98 105. 49 97. 96 5. 49 -2. 04 7 96 94. 51 89. 58 -5. 49 -10. 42 8 86 93. 41 98. 84 -6. 59 -1. 16 9 85 104. 40 111. 76 4. 40 0. 12 10 95

Índices Complejos Sintetizan varias series, productos o artículos observados para simplificarlos en una sola serie de números Índices. Según la forma de distribución al cual se distribuye.

Índices Complejos Ponderados Para poder obtener un resultado más confiable a veces es necesario incluir las relaciones entre el precio de un bien con respecto a la cantidad consumida de dicho artículo mediante el coeficiente de ponderación que lo realizaremos en base a dichos indicadores más conocidos como los Índices complejos ponderados de Laspeyre, Paasche y Fischer. Existen dos métodos principales para calcular índices de precios: • El índice de Laspeyres ó método del año base (del economista alemán Etienne Laspeyres) • El índice Paasche ó Método del año dado (del economista alemán Hermann Paasche)

Fórmulas

ÍNDICE DE FISCHER Un tercer índice, el índice de Fisher (del economista estadounidense Irving Fischer), intenta mitigar este problema, siendo una especie de resultado intermedio de los dos anteriores; calcula el Promedio Geométrico de los dos anteriores:

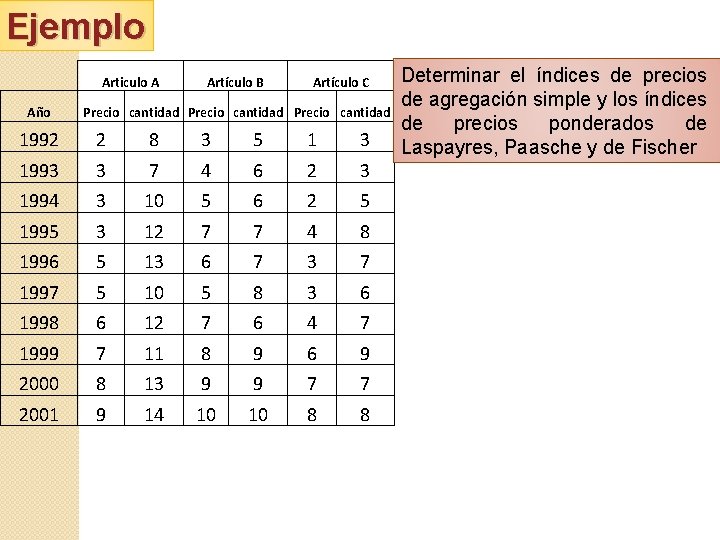
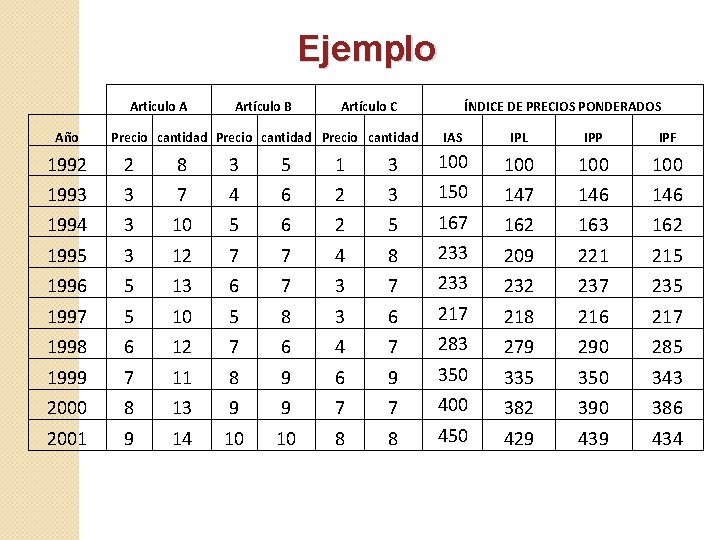
Ejemplo Articulo A Año Artículo B Artículo C Precio cantidad 1992 2 8 3 5 1 3 1993 3 7 4 6 2 3 1994 3 10 5 6 2 5 1995 3 12 7 7 4 8 1996 5 13 6 7 3 7 1997 5 10 5 8 3 6 1998 6 12 7 6 4 7 1999 7 11 8 9 6 9 2000 8 13 9 9 7 7 2001 9 14 10 10 8 8 Determinar el índices de precios de agregación simple y los índices de precios ponderados de Laspayres, Paasche y de Fischer

Ejemplo Articulo A Año Artículo B Artículo C Precio cantidad ÍNDICE DE PRECIOS PONDERADOS IAS IPL IPP IPF 1992 2 8 3 5 1 3 100 100 1993 3 7 4 6 2 3 150 147 146 1994 3 10 5 6 2 5 167 162 163 162 1995 3 12 7 7 4 8 233 209 221 215 1996 5 13 6 7 3 7 233 232 237 235 1997 5 10 5 8 3 6 217 218 216 217 1998 6 12 7 6 4 7 283 279 290 285 1999 7 11 8 9 6 9 350 335 350 343 2000 8 13 9 9 7 7 400 382 390 386 2001 9 14 10 10 8 8 450 429 434

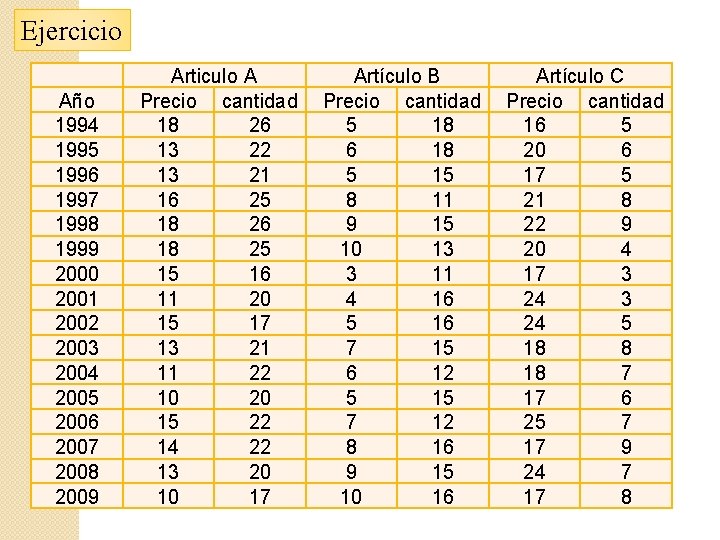
Ejercicio Año 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 Articulo A Precio cantidad 18 26 13 22 13 21 16 25 18 26 18 25 15 16 11 20 15 17 13 21 11 22 10 20 15 22 14 22 13 20 10 17 Artículo B Precio cantidad 5 18 6 18 5 15 8 11 9 15 10 13 3 11 4 16 5 16 7 15 6 12 5 15 7 12 8 16 9 15 10 16 Artículo C Precio cantidad 16 5 20 6 17 5 21 8 22 9 20 4 17 3 24 5 18 8 18 7 17 6 25 7 17 9 24 7 17 8

Tarea de Estadística para el primer parcial.

Mes 1 2 3 4 5 6 7 8 9 10 Yt 280 312 300 257 324 271 278 313 263 295 Enero 556 Febrero 534 Marzo 570 Abril 501 Mayo 552 Junio 501 Julio 504 Agosto 504 Septiembr 524 e Octubre 513 Noviembre 574 Diciembre 573 a. -) Desestacionalizar los datos. b. -) Determine el pronóstico ajustado para cada trimestre de cada año. 2001 2000 Enero 555 Febrero 500 Marzo 555 Abril 528 Mayo 582 Junio 557 Julio 585 Agosto 503 Septiembr 505 e Octubre 569 Noviembre 529 Diciembre 507 Promedio móvil n = 2, el promedio móvil ponderado (beta = 0. 60, 0. 25 y 0. 15) y el método de suavizamiento exponencial con (∞ = 0. 70); utilizando el porcentaje de error medio absoluto. PEMA

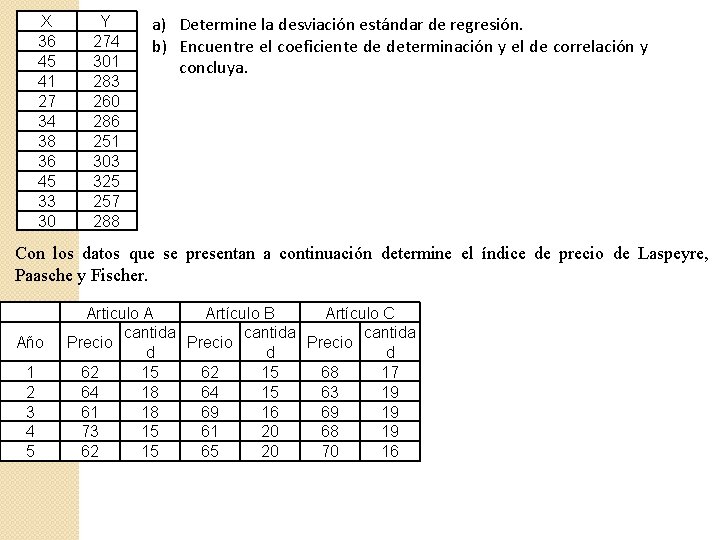
X 36 45 41 27 34 38 36 45 33 30 Y 274 301 283 260 286 251 303 325 257 288 a) Determine la desviación estándar de regresión. b) Encuentre el coeficiente de determinación y el de correlación y concluya. Con los datos que se presentan a continuación determine el índice de precio de Laspeyre, Paasche y Fischer. Año 1 2 3 4 5 Articulo A Artículo B Artículo C cantida Precio d d d 62 15 68 17 64 18 64 15 63 19 61 18 69 16 69 19 73 15 61 20 68 19 62 15 65 20 70 16