Standard Gibbs Energy of Formation The standard Gibbs

Standard Gibbs Energy of Formation The standard Gibbs energy of formation is the standard reaction Gibbs energy of formation of a compound from its elements in their reference states. Just like enthalpy, the standard Gibbs energy of a reaction can be found using the standard Gibbs energy of formation for products and reactants. What is r. G 298 for the combustion of methane? CH 4 (g) +2 O 2 (g) 2 H 2 O (l) + CO 2 (g) © Dario Bressanini

The Gibbs Energy Change (cont’d) n For the methane combustion reaction 1 CH 4(g) + 2 O 2(g) 1 CO 2(g) + 2 H 2 O(l) r. G = np f. G (products) - nr f. G (reactants) = 2 f. G [H 2 O(l)] + 1 f. G [CO 2(g)] - (7/2 f. G [O 2(g)] + 1 f. G [CH 4(g)] ) © Dario Bressanini

Free Energy Change, G, and Spontaneity n Example 15 -16: Calculate Go 298 for the reaction in Example 15 -8. Use appendix K.

The Temperature Dependence of Spontaneity n Example 15 -17: Calculate So 298 for the following reaction. In example 15 -8, we found that Ho 298= -2219. 9 k. J, and in Example 15 -16 we found that Go 298= -2108. 5 k. J.

The Temperature Dependence of Spontaneity n Example 15 -17: Calculate So 298 for the following reaction. In example 15 -8, we found that Ho 298= -2219. 9 k. J, and in Example 15 -16 we found that Go 298= -2108. 5 k. J.

The Temperature Dependence of Spontaneity

The Temperature Dependence of Spontaneity n n So 298 = -374 J/K which indicates that the disorder of the system decreases. For the reverse reaction, 3 CO 2(g) + 4 H 2 O(g) C 3 H 8(g) + 5 O 2(g) n So 298 = +374 J/K which indicates that the disorder of the system increases.

The Temperature Dependence of Spontaneity n Example 15 -18: Use thermodynamic data to estimate the normal boiling point of water.

The Temperature Dependence of Spontaneity

The Temperature Dependence of Spontaneity

The Temperature Dependence of Spontaneity

Calculating Go from Enthalpy and Entropy Values–I Problem: Potassium chlorate, one of the common oxidizing agents in explosives, fireworks, and matchheads, undergoes a solid-state redox reaction when heated, in which the oxidation number of Cl in the reactant is higher in one of the products and lower in the other (disproportionation): 4 KCl. O 3 KCl. O + KCl 3 (s) 4 (s) Use Hof and So values to calculate Gosys ( Gorxn) at 25 o. C for this reaction. Plan: To solve for Go, use Hof values to calculate Horxn( Hosys), use So values to calculate Sorxn( Sosys), and apply Equation 20. 6. Solution: Calculating Hosys from Hof values (with Equation 6. 8): Hosys = Horxn = ∑m Hof(products) ∑n Hof(reactants) = [3 mol KCl. O 4 ( Hof of KCl. O 4) + 1 mol KCl ( o of KCl. O )] [4 mol KCl. O ( H 3 f 3 © Dario Bressanini Hof of KCl)]

Calculating Go from Enthalpy and Entropy Values–II Hosys = [3 mol (-432. 8 k. J/mol) + 1 mol (-436. 7 k. J/mol)] - [4 mol (-397. 7 k. J/mol)] = -144 k. J Calculating Sosys = Sosys from So values (with Equation 20. 3): Sorxn = [3 mol KCl. O 4 ( So of KCl. O 4) + 1 mol KCl ( So of KCl)] - [4 mol KCl. O 3 (So of KCl. O 3)] = [3 mol (151. 0 J/mol K) + 1 mol (82. 6 J/mol K)] - [4 mol (143. 1 J/mol K)] = - 36. 8 J/K . Calculating Gosys = . . Gosys at 298 K: Hosys - T Sosys = -144 k. J - [(298 K)(-36. 8 J/K)(1 k. J/1000 J)] The reaction is spontaneous which is o G sys = -133 k. J © Dario Bressanini consistent with Go < 0

Effect of Temperature on Reaction Spontaneity The temperature at which a reaction occurs influences the magnitude of the T S term. By scrutinizing the signs of H and S, we can predict the effect of temperature on the sign of G and thus on the spontaneity of a process at any temperature. Temperature-independent cases (opposite signs) 1. Reaction is spontaneous at all temperatures: Ho < 0, So > 0 2 H 2 O 2 (l) 2 H 2 O(l) + O 2 (g) Ho = -196 k. J and So = 125 J/K 2. Reaction is nonspontaneous at all temperatures: Ho > 0, So < 0 3 O 2 (g) 2 O 3 (g) Ho = 286 k. J and So = - 137 J/K Temperature-dependent cases (same signs) 3. Reaction is spontaneous at higher temperature: Ho > 0 and So > 0 2 N 2 O(g) + O 2 (g) 4 NO(g) Ho = 197. 1 k. J and So = 198. 2 J/K 4. Reaction is spontaneous at lower temperature: Ho < 0 and So < 0 o = - 822. 2 k. J and o = - 181. 7 J/K Dario Bressanini 2© Na + Cl 2 Na. Cl H S (s) 2 (g) (s)

Determining the Effect of Temperature on Go–I Problem: An important reaction in the production of sulfuric acid is the oxidation of SO 2 (g) to SO 3 (g): 2 SO +O 2 SO 2 (g) 3 (g) At 298 K, Go = -141. 6 k. J; Ho = -198. 4 k. J; and So = -187. 9 J/K. (a) Use the data to decide if this reaction is spontaneous at 25 o. C and how Go will change with increasing T. (b) Assuming Ho and So are constant with T, is the reaction spontaneous at 900. o. C? Plan: (a) We examine the sign of Go to see if the reaction is spontaneous and the signs of Ho and So to see the effect of T. (b) We use Equation 20. 6 to calculate Go from the given Ho and So at the higher T (in K). Solution: Continued on next slide. © Dario Bressanini

Determining the Effect of Temperature on Go–II Solution: (a) Since Go < 0, the reaction is spontaneous at 298 K: a mixture of SO 2 (g), and SO 3 (g) in their standard states (1 atm) will spontaneously yield more SO 3 (g). With So < 0, the term -T So > 0 and becomes more positive at higher T. Therefore, Go will be less negative, and the reaction less spontaneous, with increasing T. (b) Calculating Go = Ho - T = 22. 0 k. J Since Go at 900. o. C (T= 273 + 900. = 1173 K): So = - 198. 4 k. J - [(1173 K)(-187. 9 J/K)(1 k. J/1000 J)] Go > 0, the reaction is nonspontaneous at higher T. © Dario Bressanini

Calculating G at Nonstandard Conditions–I Problem: The oxidation of SO 2, which we discussed earlier, is too slow 2 SO 2 (g) + O 2 (g) 2 SO 3 (g) at 298 K to be useful in the manufacture of sulfuric acid. To overcome this low rate, the process is conducted at an elevated temperature. (a) Calculate K at 298 K and at 973 K. Go 298 = -141. 6 k. J/mol of reaction as written; using Ho and So values at 973 K, Go 973 = -12. 12 k. J/mol of reaction as written. (b) In experiments to determine the effect of temperature on reaction spontaneity, sealed containers are filled with 0. 500 atm SO 2, 0. 0100 atm O 2, and 0. 100 atm SO 3 and kept at 25 o. C and at 700 o. C. In which direction, if any, will the reaction proceed to reach equilibrium at each temperature? (c) Calculate G for the system in part (b) at each temperature. Plan: (a) We know Go, T, and R, so we can calculate the K’s from Equation 12. 10. Dario Bressanini (b)©Calculate Q, and compare it with each K from part (a).

Calculating G at Nonstandard Conditions–II Plan : Continued (c) Since these are not standard-state pressures, we calculate G at each T from Equation 20. 11 with the values of Go (given) and Q [found in part (b)]. Solution: (a) Calculating K at the two temperatures: Go = -RT ln K so K = e-( G/RT) At 298 K, the exponent is -141. 6 k. J/mol x 1000 J 1 k. J - ( Go/RT) = = 57. 2 8. 31 J/mol K x 298 K K = e-( G/RT) = e 57. 2 = 7 x 1024 So At 973 K, the exponent is -12. 12 k. J/mol x 1000 J 1 k. J - ( Go/RT) = = 1. 50 8. 31 J/mol K x 973 K . . © Dario Bressanini K = e-( G/RT) = e 1. 50 = 4. 5

Calculating G at Nonstandard Conditions-III (b) Calculating the value of Q : p 2 SO 3 2 0. 100 Q= 2 = = 4. 00 2 p SO 2 x p. O 2 0. 500 x 0. 0100 Since Q < K at both temperatures, the denominator will decrease and the numerator increase–more SO 3 will form–until Q equals K. However, at 298 K, the reaction will go far to the right before reaching equilibrium, whereas at 973 K, it will move only slightly to the right. (c) Calculating G, the nonstandard free energy change, at 298 K and 973 K G 298 = Go + RT ln Q = -141. 6 k. J/mol + (8. 31 J/mol K x 1 k. J x 298 K x ln 4. 00) 1000 J = -138. 2 k. J/mol . G 973 = Go + RT ln Q = - 12. 12 k. J/mol + (8. 31 J/mol K x 1 k. J x 973 K x ln 4. 00 1000 J © Dario Bressanini = - 0. 90 k. J/mol .
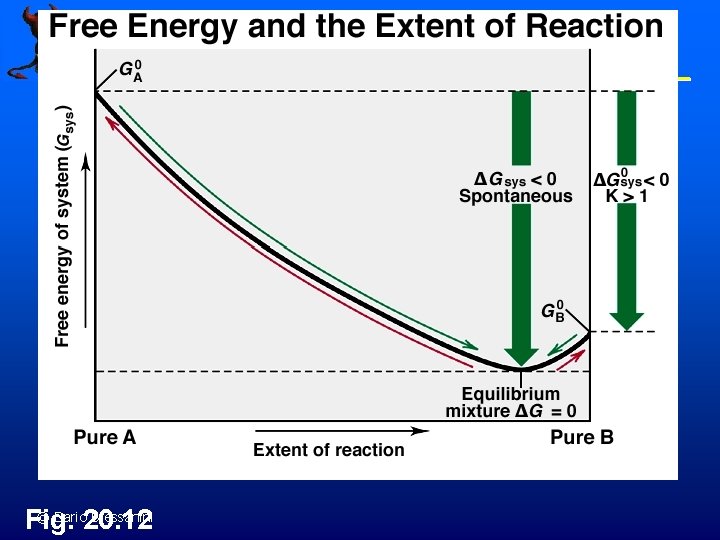
© Dario Bressanini Fig. 20. 12

Calculating Gorxn for NH 4 NO 3(s) EXAMPLE 2: NH 4 NO 3(s) NH 4 NO 3(aq) Is the dissolution of ammonium nitrate product-favored? If so, is it enthalpy- or entropy-driven? © Dario Bressanini 9_amnit. mov 20 m 07 vd 1. mov

o G rxn for NH 4 NO 3(s) NH 4 NO 3(aq) From tables of thermodynamic data we find Horxn = +25. 7 k. J Sorxn = +108. 7 J/K or +0. 1087 k. J/K Gorxn = +25. 7 k. J - (298 K)(+0. 1087 k. J/K) = -6. 7 k. J Reaction is product-favored © Dario Bressanini o

Calculating o G rxn Gorxn = S Gfo (products) - S Gfo (reactants) EXAMPLE 3: Combustion of carbon C(graphite) + O 2(g) CO 2(g) Gorxn = Gfo(CO 2) - [ Gfo(graph) + Gfo(O 2)] Gorxn = -394. 4 k. J - [ 0 + 0] Note that free energy of formation of an element in its standard state is 0. Go = -394. 4 k. J © Dario Bressanini

Go for COUPLED CHEMICAL REACTIONS Reduction of iron oxide by CO is an example of using TWO reactions coupled to each other in order to drive a thermodynamically forbidden reaction: Fe 2 O 3(s) 4 Fe(s) + 3/2 O 2(g) Gorxn = +742 k. J with a thermodynamically allowed reaction: 3/2 C(s) + 3/2 O 2 (g) 3/2 CO 2(g) Overall : Gorxn = -592 k. J Fe 2 O 3(s) + 3/2 C(s) 2 Fe(s) + 3/2 CO 2(g) Gorxn= +301 k. J @ 25 o. C BUT Gorxn < 0 k. J for T > 563 o. C See Kotz, pp 933 -935 for analysis of thermite reaction © Dario Bressanini

Other examples of coupled reactions: Copper smelting Cu 2 S (s) 2 Cu (s) + S (s) Couple this with: S (s) + O 2 (g) SO 2 (s) Overall: Gorxn= +86. 2 k. J (FORBIDDEN) Gorxn= -300. 1 k. J Cu 2 S (s) + O 2 (g) 2 Cu (s) + SO 2 (s) Gorxn= +86. 2 k. J + -300. 1 k. J = -213. 9 k. J (ALLOWED) Coupled reactions VERY COMMON in Biochemistry : e. g. all bio-synthesis driven by ATP ADP for which Horxn = -20 k. J Sorxn = +34 J/K Gorxn = -30 k. J @ 37 o. C © Dario Bressanini
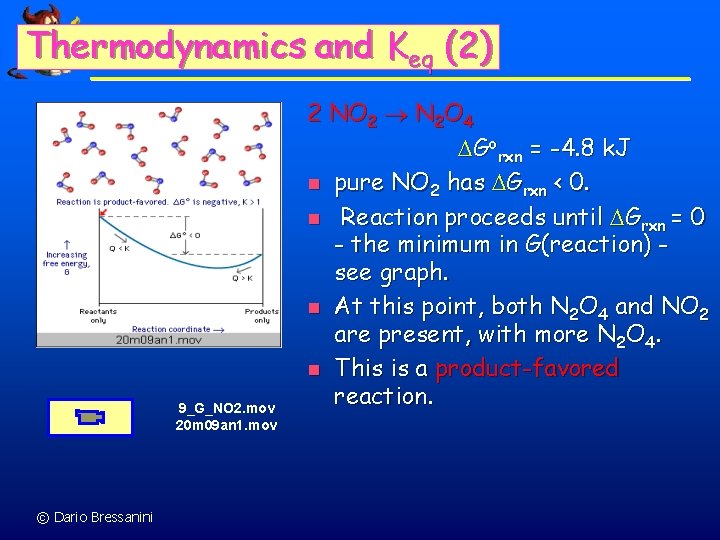
Thermodynamics and Keq (2) 9_G_NO 2. mov 20 m 09 an 1. mov © Dario Bressanini 2 NO 2 N 2 O 4 Gorxn = -4. 8 k. J n pure NO 2 has Grxn < 0. n Reaction proceeds until Grxn = 0 - the minimum in G(reaction) see graph. n At this point, both N 2 O 4 and NO 2 are present, with more N 2 O 4. n This is a product-favored reaction.
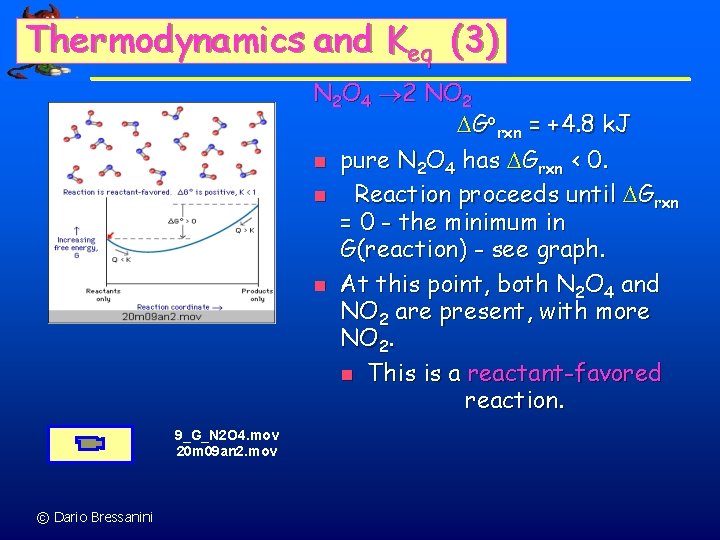
Thermodynamics and Keq (3) N 2 O 4 2 NO 2 Gorxn = +4. 8 k. J n pure N 2 O 4 has Grxn < 0. n Reaction proceeds until Grxn = 0 - the minimum in G(reaction) - see graph. n At this point, both N 2 O 4 and NO 2 are present, with more NO 2. n This is a reactant-favored reaction. 9_G_N 2 O 4. mov 20 m 09 an 2. mov © Dario Bressanini

Thermodynamics and Keq (5) Gorxn = - RT ln. K Calculate K for the reaction N 2 O 4 2 NO 2 Gorxn = +4. 8 k. J Gorxn = +4800 J = - (8. 31 J/K)(298 K) ln K K = 0. 14 When Gorxn > 0, then K < 1 - reactant favoured When Gorxn < 0, then K >1 - product favoured © Dario Bressanini

Consider the synthesis of methanol: CO(g) + H 2(g) CH 3 OH(l) Calculate G at 25 o. C for this reaction where CO(g) at 5. 0 atm and H 2(g) at 3. 0 atm are converted to CH 3 OH(l). Given: Gf (CH 3 OH(l)) Gf (CO(g)) © Dario Bressanini Gf (H 2(g)) = − 166 k. J = − 137 k. J =0

Cont’ We must use: G = G + RT ln(Q) G = Gf - Gf (CH 3 OH(l)) (CO(g)) (H 2(g)) G = -166 -(-137)-0 = -29 k. J Q= 1 PCO. P 2 H 2 = 1 (5). (3)2 = 2. 2 x 10 -2 G = -29 x 103 + (8. 3145)(298) ln( 2. 2 x 10 -2) = − 38 k. J / mol © Dario Bressanini

The second law is the greatest good and the greatest bad on earth. © Dario Bressanini

The good: Life is possible. We eat concentrated energy in the form of food, process that energy to synthesize complex biochemicals and run our organism, excreting diffused energy as body heat and less concentrated energy substances. We use concentrated energy fuels to gather all kinds of materials from all parts of the world and, without any energetic limitation, arrange them in ways that please us. We affect non-spontaneous reactions (pure metals from ores, synthesizing curative drugs from simple compounds, altering DNA). We make machines that make other machines, machines that © Dario Bressanini mow lawns, move mountains, and go to the moon.

The bad: Life is always threatened. Every organic chemical of the 10, 000 different kinds in our bodies is metastable, synthesized by a nonspontaneous reaction and kept from instant oxidation in air by activation energies. Living creatures are energy processing systems that cannot function unless biochemical cycles operate synchronically to use energy to oppose second law predictions. All of the biochemical systems that run our bodies are maintained and regulated by feedback subsystems, composed of complex substances that are synthesized internally by thermodynamically nonspontaneous reactions, affected by utilizing energy ultimately transferred from the metabolism of food. When these feedback subsystems fail energy can no longer be processed to carry out the many reactions we need for life that are contrary to the direction © Dario Bressanini predicted by the second law.
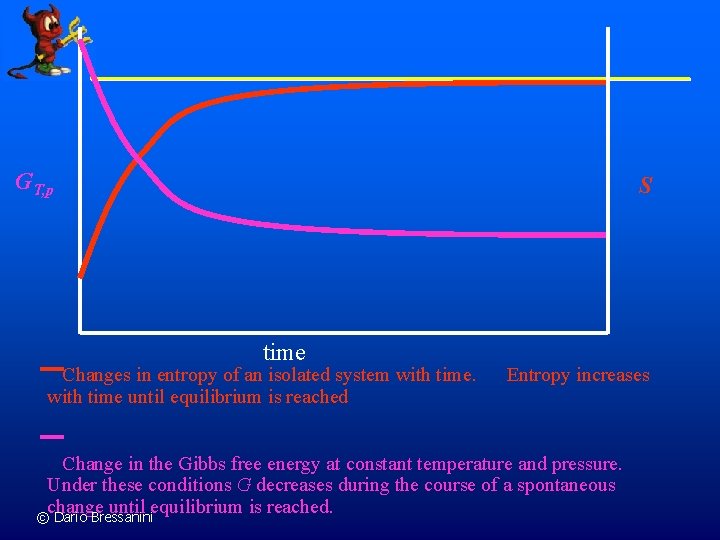
GT, p S time Changes in entropy of an isolated system with time until equilibrium is reached Entropy increases Change in the Gibbs free energy at constant temperature and pressure. Under these conditions G decreases during the course of a spontaneous change until equilibrium is reached. © Dario Bressanini
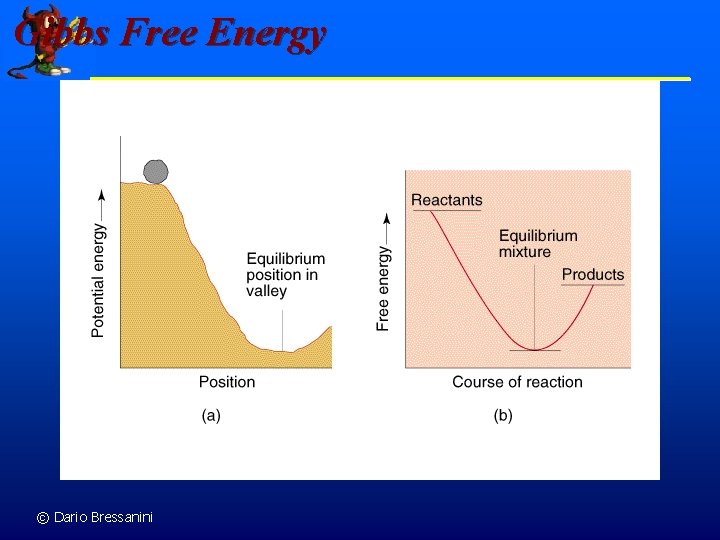
Gibbs Free Energy © Dario Bressanini

Chemical Potentials of the Ideal Gas n Differentiating the chemical potential with temperature © Dario Bressanini

The Standard Chemical Potential n For P 1 = P = 1 bar, we define the standard state chemical potential °= (T, 1 bar) © Dario Bressanini

The Chemical Potential for Real Gases n n The fugacity (f) represents the chemical potential of a real gas. Define the fugacity coefficient =f/P n For a real gas © Dario Bressanini

Obtaining Fugacity Coefficients n Comparing the chemical potential of the real gas to the chemical potential of an ideal gas at the same pressure © Dario Bressanini

Calculating Fugacity Coefficients n The fugacity coefficients are obtained from the compression factors (Z) as shown below © Dario Bressanini

Partial molar (molal) quantities n If system is not simple, e. g. open system or mixtures, then for e. g. substances A and B n (see lab manual, the five pages following error analysis) n For constant T, P and n. A (e. g. 1 kg water in expt 2) V n Find V does not vary linearly with n. B Slope = partial molar volume m. B = moles solute / kg solvent © Dario Bressanini

Note: at constant T and P, the total volume of the solution is: n n Vm, A, Vm, B are constant for a given composition i. e. think of making up a solution at constant composition. Then V = Vm, A n. A + Vm, B n n A similar equation applies for any partial molar quantity. © Dario Bressanini

DEFINE the chemical potential, or partial molar free energy, of A n n n n The exact differential for G is Compare with combined law eqn (CL. G) d. G + Sd. T - Vd. P = dw¢rev£ dw¢ d. G = - Sd. T + Vd. P + idni G=A+PV d. A+Pd. V+Vd. P = - Sd. T + Vd. P + idni d. A = -Pd. V - Sd. T + idni and this the most useful defn. , as it is the only one written in terms of intensive variables. © Dario Bressanini

recall: n n n Criteria for equilibrium: d. G = - Sd. T + Vd. P + idni For a reversible, equilibrium process (we’ll take dw¢ = 0), such as a phase change or chemical reaction (at const. T, P) ice ( ice - liquid )dn = 0 n i. e. equilibrium requires n Hence criteria for equilibrium ice = liquid n equal T n equal P mechanical equil n equal © Dario Bressanini thermal equil chemical equil liquid -dnice = dnliquid
- Slides: 44