Chapter 17 Free Energy And Thermodynamics I Directionality






























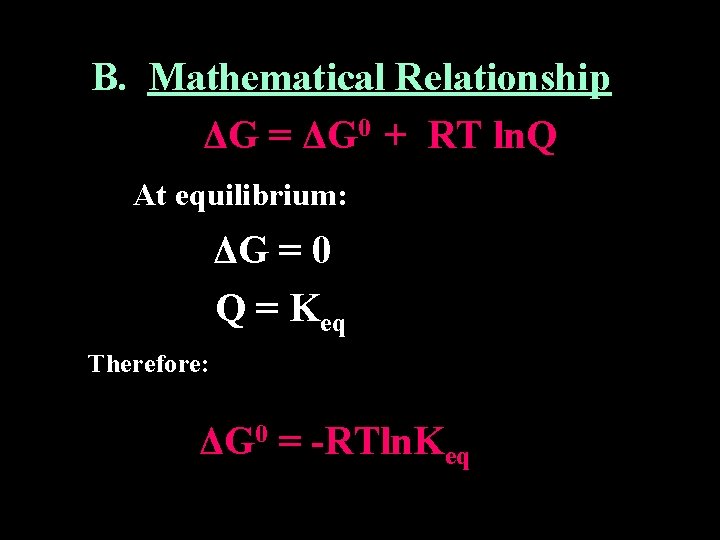







- Slides: 43

Chapter 17 Free Energy And Thermodynamics

I. Directionality of Reactions Question? Why do some reactions (processes) occur in one direction while others in another? A. Product-Favored Reactions (Processes) 1. Occurs spontaneously, as written from left to right, without outside help or intervention. 2. Kc >1 3. Reaction occurs on its own 4. Tells us nothing about rate (speed of reaction)

B. Reactant-Favored Reactions (Processes) 1. Occurs nonspontaneously as written from left to right. 2. Kc < 1 3. Reaction tends to proceed in opposite direction as written. 4. Tells us nothing about the rate or speed of reaction. Examples of Each Type Significance of being able to understand predict direction. (Is reaction spontaneous? )

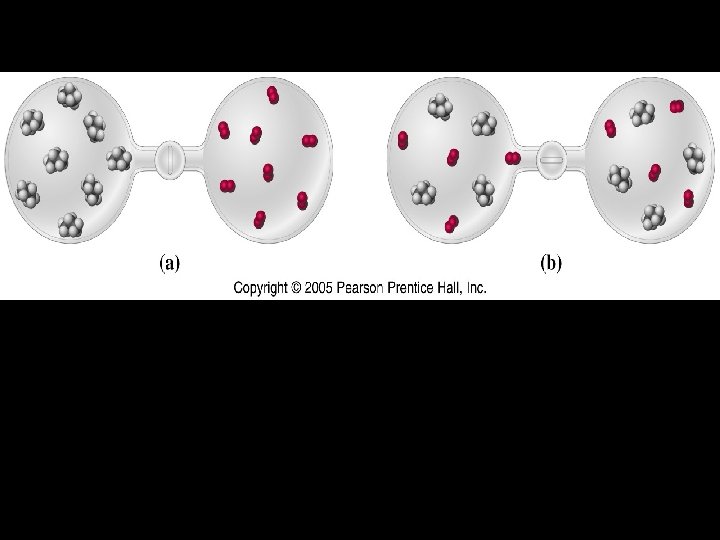
II. Probability and Chemical Rxns (Factors Affecting Direction of Rxn) Dispersal of Energy What is the likely flow of energy in a natural process? 1. If a thousand bricks are dropped from an airplane, would you expect them to land in the form of a brick wall? 2. If you dropped a mixed deck of cards, would you expect them to land in order? 3. Would you expect the elevated circle of water around where a rock fell to remain motionless?

4. Would you expect one end of a metal rod to spontaneously get hot while the other end gets cold? Dispersal of Energy occurs because the probability is much higher that energy will be spread over many particles than that it will be concentrated in a few. Entropy , “S”, is a measure of the randomness or disorder of energy. It relates macroscopically to the randomness or disorder on the molecular scale.


Example – Melting of Ice At 250 C (Room Temp) H 2 O (s) → H 2 O (l) Is the system exothermic? (ΔH “+” or “-”? ) Is the process product-favored (spontaneous)? Why?


Explanation Both enthalpy (ΔH) and entropy (ΔS) for the system are important in determining whether the process is spontaneous (product-favored) or not. Process (at 250 C) is spontaneous because entropy of system is more significant factor in this case.

III. Closer Look At Entropy A. Qualitative Guidelines for Predicting Entropy of Process or Reaction 1. Entropy of gases are generally much larger than those of liquids, which in turn are larger than those of solids.

Therefore, entropy increases when: Solids melt to form liquids. Solids or liquids vaporize to form gases. 2. Entropies of more complex molecules are larger than those of simpler molecules, especially in a series of closely related compounds. The more atoms in molecules (higher molar mass), the greater is the entropy of the substance. 3. Entropies of ionic solids are larger the weaker the attractions among the ions.

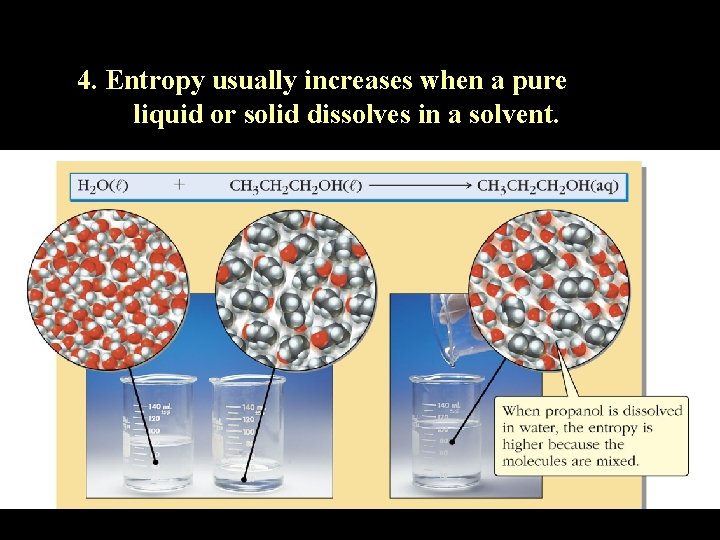
4. Entropy usually increases when a pure liquid or solid dissolves in a solvent.

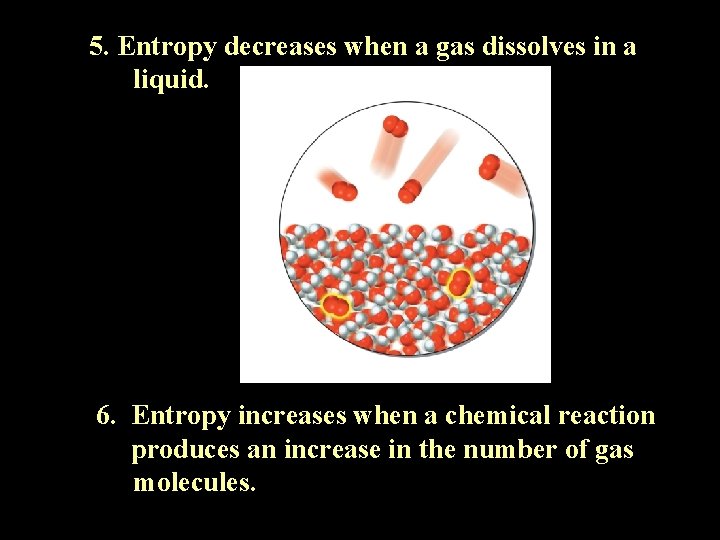
5. Entropy decreases when a gas dissolves in a liquid. 6. Entropy increases when a chemical reaction produces an increase in the number of gas molecules.

Predict whether the entropy change will be positive or negative for each reaction or system. Explain your answer. Na. Cl(s) Na+ (aq) + Cl-(aq) CO 2(g) + Mg. O(s) Mg. CO 3(s) H 2 O(g) H 2 O(l) N 2(g) + 3 H 2(g) 2 NH 3(g)

B. Absolute Entropy Values 1. Entropy can be measured with calorimeter for a process that takes place at constant T and P. ΔS = q/T (T in Kelvin scale) 2. Entropy is temperature dependent. (predicted by Kinetic Molecular Theory) 3. What happens to entropy when T = 0 K?

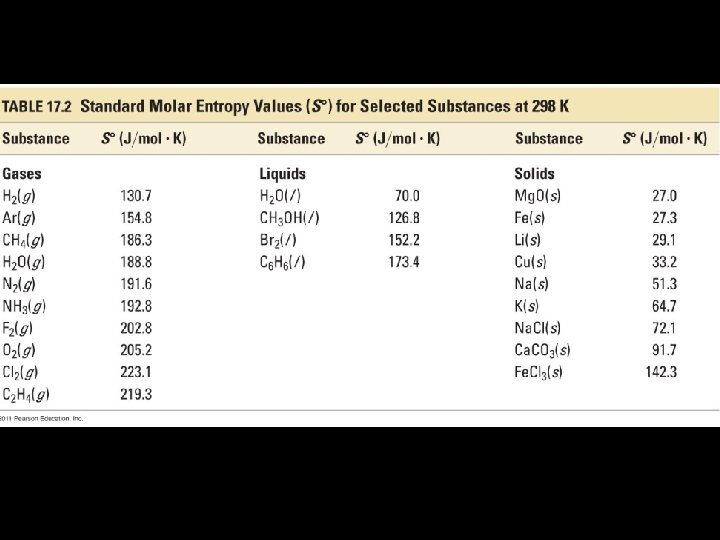
4. Third Law of Thermodynamics- the entropy of a perfect crystal = 0 at absolute zero. 5. Standard Molar Entropy Values can be determined. See Appendix II or Table 17. 2 S 0 = J / K mol (at 298 K) 6. Remember these are absolute values for both elements and compounds. ( Not like ΔH values which were measured relative to elements in their most stable state. Standard enthalpies of formation (ΔH 0 f) of elements are arbitrarily set to zero. )


C. Entropy Calculations 1. Determining the Entropy Change For a Reaction (System) “Since entropy is a state function and is thus path independent, we can use a Hess=s Law type calculation. Remember we are working with absolute entropies. ” ΔS 0 rxn = S 0 products - S 0 reactants ΔS 0 rxn = ∑{(moles of prod. )x So(prod. )} ∑{(moles of react. )x So(react. )}

Example Problem: Calculate the standard entropy change (ΔS 0) for the following reaction. Standard molar entropies are found in Appendix J or Table 18. 1. S 0 (J K-1 mol-1) 2 CO(g) + O 2(g) 2 CO 2(g) 197. 6 205. 1 213. 7 What is the standard entropy change for the reaction: 2 CO 2(g) 2 CO(g) + O 2(g) ?

Example : Freezing of Water At -100 C (Below FP of Water) H 2 O (l) → H 2 O (s) Is the system exothermic? (ΔH “+” or “-”? ) Is ΔS for the system “+” or “-” ? Is the process product-favored (spontaneous) at -100 C ? Why?

Explanation Both enthalpy (ΔH) and entropy (ΔS) for the system are important in determining whether the process is spontaneous (product-favored) or not. Process (at -100 C) is spontaneous. Let’s explain why relative to total entropy of universe.

D. Entropy and the Second Law of Thermodynamics “The total entropy of the universe (the system plus its surroundings) always increases for a spontaneous process. ” ΔSuniverse = ΔSsystem + Δssurroundings Δsuniverse > O (or “+” ) We have calculated ΔSsystem = ΔSreaction by using Hess’s Law. If we can determine ΔSsurroundings , we can predict whether a reaction is product favored (spontaneous).

Calculate ΔH for the reaction and assume that this quantity of thermal energy is transferred reversibly to or from the surroundings. ΔSsurroundings = - ΔHrxn / T Therefore: We could use this information to predict if reaction is product favored. But lets simplify.

Multiply both sides by –T(Kelvin scale) : Simplify and rearrange: Define Free Energy:

IV. Gibbs Free Energy A. Definition of Gibbs Free Energy 1. New thermodynamic function, G 2. ΔG = -TΔSuniverse 3. If entropy of universe increases, the Gibbs free energy must decrease (have a “-” sign). 4. Plugging into previous equation (under standard conditions gives: ΔG 0 = ΔH 0 – TΔS 0

ΔG 0 = ΔH 0 – TΔS 0 If ΔG 0 is negative (-), the reaction is product-favored (spontaneous). If ΔG 0 is positive (+), the reaction is reactant-favored (nonspontaneous) To predict the direction of reaction:

Spontaneous or Product. Favored? ΔG 0 = ΔH 0 - TΔS 0 Yes - - + Yes, low T No, high T ? - - No, low T Yes, high T ? + + No + + -


B. Free Energy Calculations Two Methods 1. From ΔH 0 and ΔS 0 Values ΔG 0 = ΔH 0 - T ΔS 0 2. From Hess’s Law Type Calculation (from Table of Standard Free Energies of Formation – see Appendix II or Table 17. 3 ΔGo = ∑{(moles of prod. ) Gof (prod. )} - ∑{(moles of react. ) Gof (react. )}


1. Calculate ΔG 0 for the reaction below. 2 Fe 2 O 3(s) + 3 C(gr) 4 Fe(s) + 3 CO 2 (g) ΔHof -824. 2 o 0 -393. 5 S 0 87. 4 5. 74 27. 78 ΔGof -742. 1 0 0 (ΔHof and ΔGof in k. J/mol, S 0 in J/K mol) 213. 7 -394. 4 a. Is the reaction endothermic or exothermic? b. Does entropy increase or decrease for the reaction? (Predict first, then verify) c. Is the reaction product-favored or reactantfavored?

V. Temperature Effects and Reaction Direction A. Explanation 1. A reaction may be product-favored at one temperature and reactant-favored at another. 2. How can we estimate that temperature? Its where ΔGrxn equals zero. (ΔGrxn will switch from “-” to “+’ or switch from “+” to “-” at that T. ΔG 0 = ΔH 0 – TΔS 0 T = ΔH 0 / ΔS 0

B. Problem For the reaction previously discussed: 2 Fe 2 O 3(s) + 3 C(gr) 4 Fe(s) + 3 CO 2 (g) the following thermodynamic data was determined. ΔH 0 rxn = +467. 9 k. J ΔG 0 rxn = +301. 0 k. J ΔS 0 rxn = +560. 2 J/K 1. What is ΔG 0 rxn at 250 C ? 2. Determine (estimate) ΔGrxn at 500 Kelvin. 3. At what temperature will the reaction become product-favored or exergonic?

VI. Free Energy & Equilibrium A. ΔG and K Give Similar Information ** ΔG (Gibbs Free Energy) tells you whether a reaction is spontaneous or not. It tells you whether a reaction will proceed to products or not. ** K (equilibrium constant) tells you how much product or reactants will be present at equilibrium. It tells you whether a reaction will proceed to product or not.
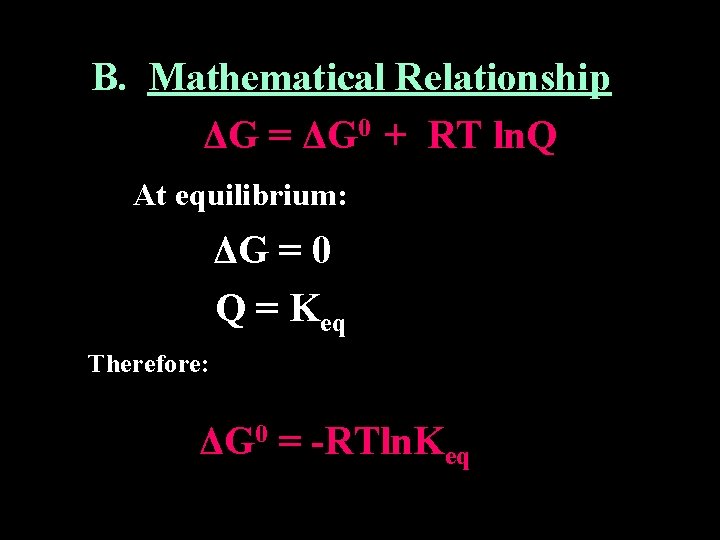
B. Mathematical Relationship ΔG = ΔG 0 + RT ln. Q At equilibrium: ΔG = 0 Q = Keq Therefore: ΔG 0 = -RTln. Keq

ΔG 0 = -RTln. Keq 1) T = temperature in Kelvin scale 2) R = gas constant (8. 314 J / mol K) 3) Keq = Kc for reactions involving solutions 4) Keq = Kp for reactions involving gases 5) Keq = Ksp for equlibrium of slightly soluble salts ΔGo Keq Product -Favored Positive <1 no Negative >1 yes zero 1 neither

C. Problem Solving 1. Determination of Free Energy The following reaction conducted at a temperature of 968 K, was found to have an equilibrium constant of Kp = 49. 7. H 2(g) + I 2(g) 2 HI(g) Is the reaction product favored? What is the value of the standard Gibbs Free Energy for the reaction at this temperature?

2. Determination of Equilibrium Constant Answer the following questions for the reaction and information provided. 2 Cl 2(g) + 2 H 2 O(g) 4 HCl(g) + O 2 (g) ΔHof 0 -241. 82 -92. 31 0 S 0 223. 07 188. 83 186. 91 205. 14 ΔGof 0 -228. 57 -95. 30 0 (ΔHof and ΔGof in k. J/mol, S 0 in J/K mol) a. Determine the equilibrium constant for the reaction at 298 K. b. Is the reaction reactant or product favored at 298 K?

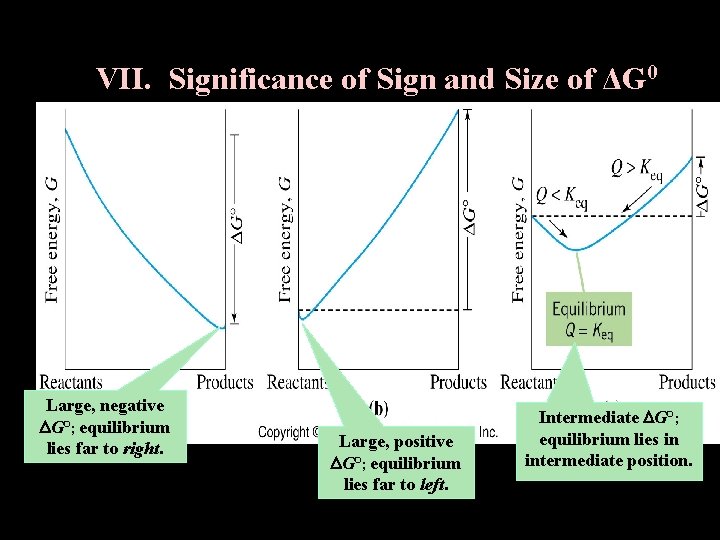
VII. Significance of Sign and Size of ΔG 0 Large, negative G°; equilibrium lies far to right. Large, positive G°; equilibrium lies far to left. Intermediate G°; equilibrium lies in intermediate position.

VIII. Gibbs Free Energy and Maximum Work ΔG represents the maximum useful work that can be done by a product favored-reaction on the surroundings. Calculate the maximum useful work (energy) that can be produced from the complete combustion of 8. 0 g of methane under standard conditions?

IX. Coupling Reactions and Metabolism Glucose is degraded in our body through a series of chemical reactions which is called a metabolic pathway (glycolysis). glucose 6 -P glyceraldehyde 3 -P 3 -phosphoglycerate fructose 6 -P fructose 1, 6 -BP pyruvate

Consider the first reaction: glucose + Pi glucose 6 -P + H 2 O ΔG 0 = + 13. 8 k. J How can this reaction occur in the body? By coupling of reactions glucose + Pi glucose 6 -P + H 2 O ΔG 0 = + 13. 8 k. J ATP + H 2 O ADP + Pi ΔG 0 = - 30. 5 k. J glucose + ATP glucose 6 -P + ADP ΔG 0 = - 16. 7 k. J Net coupled reaction is product-favored and metabolic pathway may continue to occur!!

X. Thermodynamic vs. Kinetic Stability Thermodynamically Stable: if a substance does not undergo product-favored reactions. Kinetically Stable: if a substance may be involved in a product-favored reaction, but it is so slow that the substance is stable. Example: Aluminum (in soda cans) Thermodynamically unstable: 4 Al(s) + 3 O 2(g) 2 Al 2 O 3(s) ΔG 0 = - 3164. 6 k. J Aluminum cans do not decompose readily, Why? ?
 Chapter 8 blood and blood spatter
Chapter 8 blood and blood spatter Projected blood stains
Projected blood stains Helmholtz free energy
Helmholtz free energy Gibbs free energy spontaneous
Gibbs free energy spontaneous Gibbs free energy equation
Gibbs free energy equation Delta g = rt ln(q/k)
Delta g = rt ln(q/k) Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Entropy equation temperature
Entropy equation temperature Energy balance equation thermodynamics open system
Energy balance equation thermodynamics open system Internal energy
Internal energy Laws in thermodynamics
Laws in thermodynamics First law of energy conservation
First law of energy conservation Internal energy formula thermodynamics
Internal energy formula thermodynamics Formula thermal energy
Formula thermal energy The story of an hour summary
The story of an hour summary Free hearts free foreheads you and i are
Free hearts free foreheads you and i are Reschual
Reschual Chemical engineering thermodynamics 8th solution chapter 3
Chemical engineering thermodynamics 8th solution chapter 3 Chemical engineering thermodynamics 8th solution chapter 4
Chemical engineering thermodynamics 8th solution chapter 4 Chemical engineering thermodynamics 8th solution chapter 6
Chemical engineering thermodynamics 8th solution chapter 6 Control mass system
Control mass system Chemical engineering thermodynamics 8th solution chapter 10
Chemical engineering thermodynamics 8th solution chapter 10 Thermodynamics chapter 4
Thermodynamics chapter 4 Chemical engineering thermodynamics 8th solution chapter 10
Chemical engineering thermodynamics 8th solution chapter 10 Heat capacity
Heat capacity Q=w/j
Q=w/j Thermodynamics chapter 2
Thermodynamics chapter 2 Chapter 7 energy conservation of energy
Chapter 7 energy conservation of energy A free map determines which blocks are free, allocated.
A free map determines which blocks are free, allocated. Free free absorption
Free free absorption Relationship between entropy and free energy
Relationship between entropy and free energy Chemistry microstates
Chemistry microstates How to calculate gibbs free energy with partial pressures
How to calculate gibbs free energy with partial pressures Phosphoanhydride bond
Phosphoanhydride bond Entropy and gibbs free energy
Entropy and gibbs free energy Ap chemistry spontaneity entropy and free energy
Ap chemistry spontaneity entropy and free energy Thermodynamics cengel and boles
Thermodynamics cengel and boles Introduction and basic concepts of thermodynamics
Introduction and basic concepts of thermodynamics Irreversible process in thermodynamics
Irreversible process in thermodynamics Thermodynamics introduction and basic concepts
Thermodynamics introduction and basic concepts Thermodynamics enthalpy of reaction and hess's law
Thermodynamics enthalpy of reaction and hess's law Entropy
Entropy Thermodynamic intensive properties
Thermodynamic intensive properties