Rozwizywanie ukadw rwna Metody skoczone eliminacyjne Zasady metod

Rozwiązywanie układów równań Metody skończone (eliminacyjne)

Zasady metod eliminacyjnych n Dotyczą układów równań liniowych n Polegają na stopniowym przekształceniu macierzy współczynników do postaci trójkątnej lub diagonalnej n Wykorzystują właściwości macierzy: – Mnożenie wiersza przez liczbę – Odejmowanie wierszy od siebie

Metoda eliminacji Gaussa n Metoda: – Przekształcenie macierzy współczynników do macierzy trójkątnej ze współczynnikami równymi 1 na przekątnej – Wyliczenie x n – Wyliczenie kolejnych x n-i (i=1. . n-1) – Wymaga wykonania około n 3/3 operacji mnożenia i dzielenia

Metoda eliminacji Gaussa n Algorytm 1. Wczytać liczbę równań n, macierz współczynników i wektor wyrazów wolnych jako jedną macierz a (n, n+1) 2. Wybrać wiersz pierwszy i=1 3. Wszystkie współczynniki i wyraz wolny wybranego wiersza podzielić przez współczynnik w kolumnie o numerze wybranego w p. 2. (i-tego) wiersza a(i, j)=a(i, j)/a(i, i) dla j=i. . n+1

Metoda eliminacji Gaussa 4. Wybrać wiersz eliminowany k=i+1 5. Określić mnożnik: parametr w wierszu eliminowanym, w kolumnie=wierszowi wybranemu: m=a(k, i) 6. Przyjąć a(k, i)=0 i odjąć od parametrów wiersza eliminowanego parametry wiersza wybranego pomnożone przez mnożnik: a(k, j)=a(k, j)-m*a(i, j) dla j=k. . n+1 7. Wybrać kolejny wiersz eliminowany k=k+1 i wrócić do p. 5 o ile wiersz kolejny jest <= n 8. Wybrać kolejny wiersz i=i+1 i przejść do p. 3 o ile i < n

Metoda eliminacji Gaussa 9. Obliczyć a(i, i+1)= a(i, i+1)/a(i, i) 10. Obliczyć x(i) = a(i, i+1) 11. Przyjąć licznik j wiekszy od i o 1, jeżeli j>n-1 to przejść do 14 12. Obliczyć x(i)=x(i)-x(j)*a(i, j) 13. Zwiększyć j o 1 i jeżeli j<n przejść do p. 12 14. Zmniejszyć i o 1 i jeżeli większe od 0 to przejść do p. 10 15. Wydrukować x

Inne metody skończone n Metoda Jordana – Prowadzi do utrzymania macierzy diagonalnej – odpadają obliczenia „wsteczne” – Pierwsza eliminacja jest identyczna jak w metodzie Gaussa – Od drugiej eliminacji eliminuje się elementy także w wierszach powyżej wiersza wybranego – Wymaga n 3/2 operacji mnożenia i dzielenia – Korzystna tylko w przypadku obliczeń dla wielu wektorów rozwiązań

Inne metody skończone n Metoda Cholesky’ego (Banachiewicza) – Dotyczy symetrycznej macierzy współczynników – Pozwala znaleźć rozwiązanie wykonując n 3/6 operacji mnożenia i dzielenia

Rozwiązywanie układów równań Metody iteracyjne (nieskończone)

n Zasada metod iteracyjnych – Założenie początkowego rozwiązania układu równań – Przekształcenie układu równań do postaci – Wielokrotne wykonanie obliczeń aż różnice x po lewej i prawej stronie będą wystarczająco małe

n Metoda Jacobiego – Dominujące elementy leżą na przekątnej – Każdy wiersz dzielony przez współczynnik leżący na przekątnej (ai, i) n Metoda Gaussa-Siedla – Przyspieszenie obliczeń przez użycie, tam gdzie to możliwe, przybliżeń z kroku r+1

Metoda Jacobiego dla

Metoda Jacobiego

Metoda Gaussa-Siedla

Metody matematyczne w inżynierii chemicznej Całkowanie numeryczne

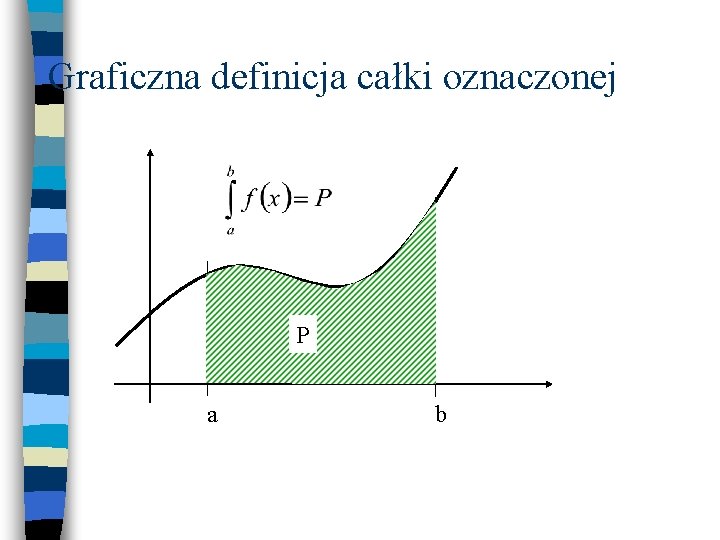
Graficzna definicja całki oznaczonej P a b

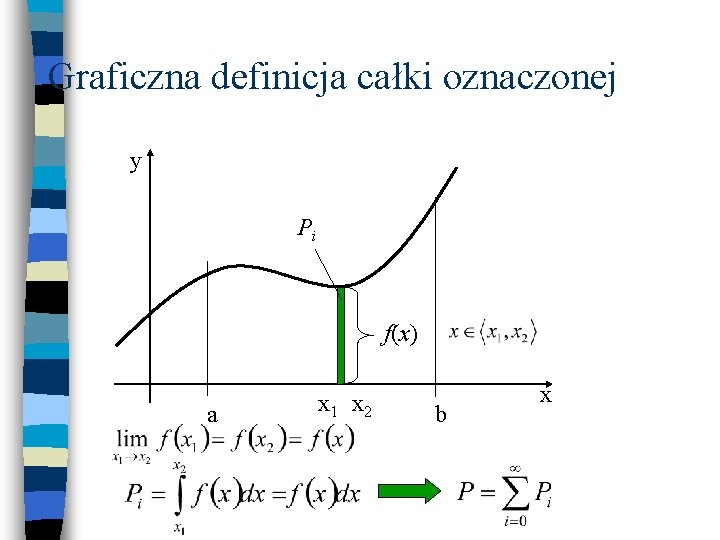
Graficzna definicja całki oznaczonej y Pi f(x) a x 1 x 2 b x

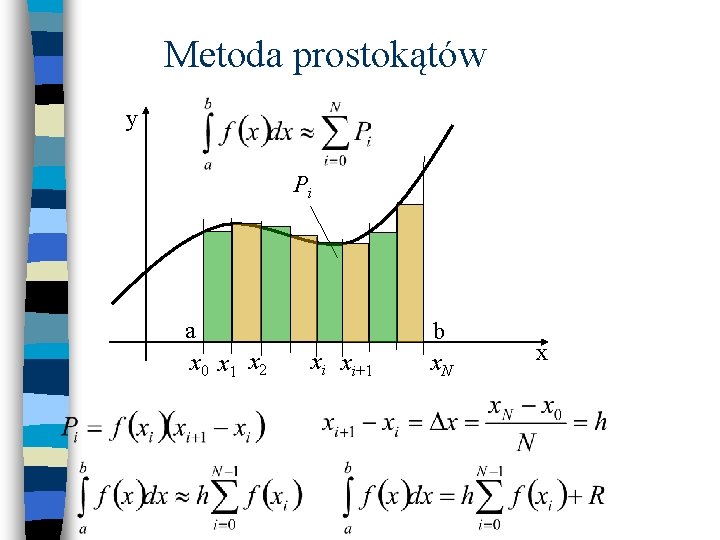
Metoda prostokątów y Pi a x 0 x 1 x 2 xi xi+1 b x. N x

Błąd metody zależność u(x)= przybliżamy (aproksymujemy) inną funkcją U(x, h) = Wymagane jest by funkcja "zastępcza" dla h 0 była zbieżna do u(x). Oznacza to, że różnica (Residuum) R musi dążyć do 0 dla h dążącego do 0

Błąd metody Dla metody istotne jest jak szybko zmniejsza się R, co można zapisać n – dodatnia liczba całkowita oznaczająca rząd metody Dla jednego kroku metoda prostokątów ma rząd n = 2 Wielokrotne użycie każdej z metoda zmniejsza rząd o 1 (kwadratura złożona) Ostatecznie

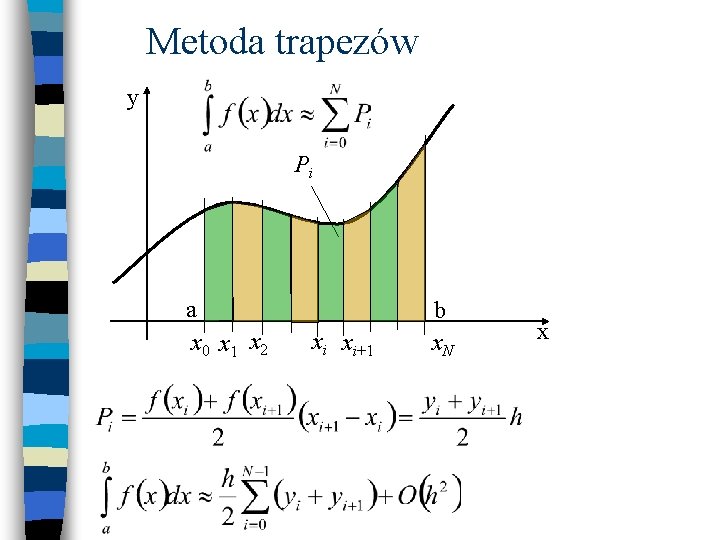
Metoda trapezów y Pi a x 0 x 1 x 2 xi xi+1 b x. N x

Metoda trapezów Ostateczny wzór na obliczanie całki metodą trapezów:

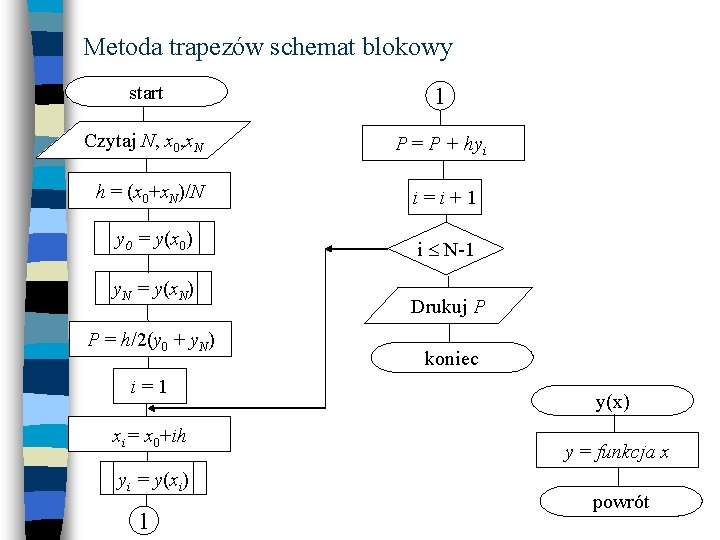
Metoda trapezów algorytm 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Przeczytaj granice całkowania, x 0 i x. N Przeczytaj ilość podziałów N Oblicz h = (x 0 - x 1)/N Oblicz y 0 i y. N Oblicz P = h/2(y 0 + y. N) Przyjmij i = 1 Oblicz xi = x 0 +ih Oblicz yi Oblicz P = P + hyi Zwiększ i o 1 (i=i+1) Jeżeli i N-1 to idź do p. 6 Drukuj P Koniec

Metoda trapezów schemat blokowy start 1 Czytaj N, x 0, x. N P = P + hyi h = (x 0+x. N)/N i=i+1 y 0 = y(x 0) i N-1 y. N = y(x. N) P = h/2(y 0 + y. N) i=1 xi = x 0+ih yi = y(xi) 1 Drukuj P koniec y(x) y = funkcja x powrót

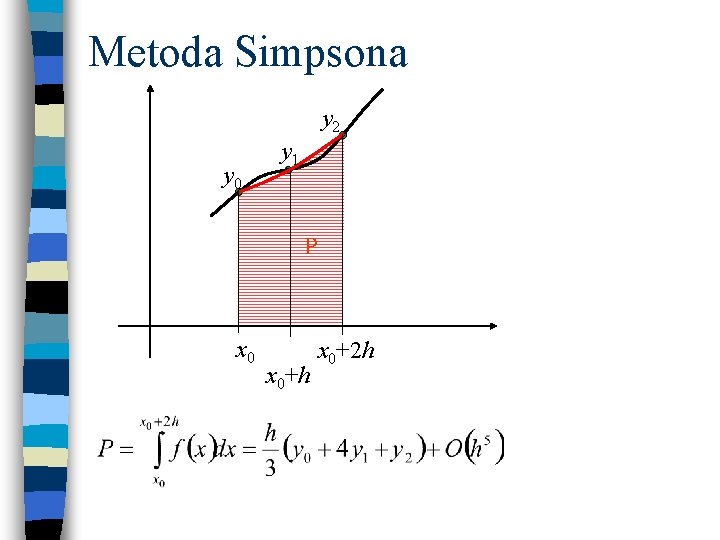
Metoda Simpsona y 2 y 0 y 1 P x 0+h x 0+2 h

Metoda Simpsona Inna postać:

Metoda Simpsona Warunki jakie musi spełniać ilość podziałów n: n 2 2. n = 2 k, gdzie k to dowolna liczba naturalna 1.

Szacowanie błędu całkowania numerycznego Ogólny wzór na przybliżoną całkę oznaczoną: Jeżeli obliczymy wartość całki dla dwóch kroków o długości h 1 = h oraz h 2 = h/2

Szacowanie błędu całkowania numerycznego błąd metody jest funkcją kroku: Zakładamy, że h jest bardzo małe Poszukujemy tylko wartości A Podstawiając h: -

Szacowanie błędu całkowania numerycznego

Szacowanie błędu całkowania numerycznego

Metoda Romberga/Richardsona Modyfikacja metody trapezów n Zwiększenie dokładności poprzez zastosowanie ekstrapolacji n http: //en. wikipedia. org/wiki/Richardson_extrapolation

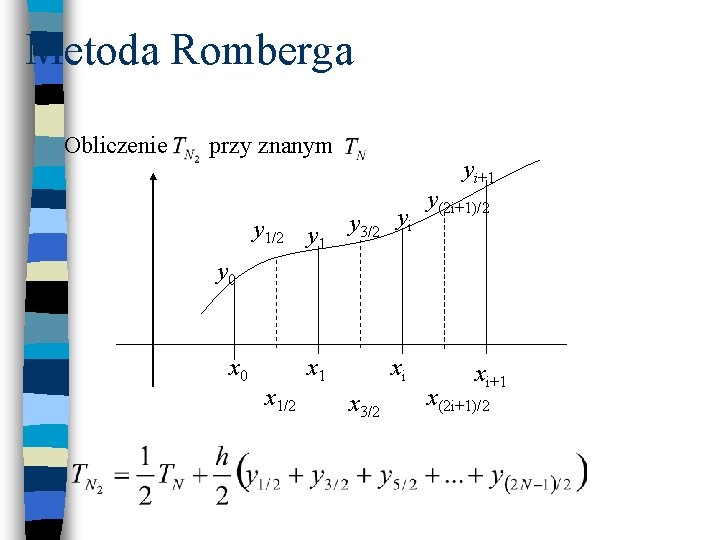
Metoda Romberga Granice całkowania <a, b> dzielimy na N części to Przybliżoną wartość całki określa wzór: Jeżeli krok zmniejszymy 2 -krotnie: W ten sam sposób obliczmy: Jest oczywiste, że dla N otrzymamy wynik pozbawiony błędu metody. Pozostaje problem błędu zaokrąglenia!

Metoda Romberga Utwórzmy nowy ciąg zgodnie z równaniami: itd. Można wykazać, że ciąg taki jest szybciej zbieżny niż ciąg pierwotny.

Metoda Romberga Można utworzyć ciąg: itd. który jest jeszcze szybciej zbieżny. Ogólnie

Metoda Romberga Obliczenie przy znanym yi+1 y 1/2 y 1 y 3/2 yi y(2 i+1)/2 y 0 x 1/2 x 1 xi x 3/2 xi+1 x(2 i+1)/2

Metoda Romberga przykład Obliczyć całkę oznaczoną: 0, 693 147 181

Ekstrapolacja Richardsona n Opiera się na obliczeniu całki przy podziale przedziału <a, b> na m 1 i m 2 części. Uzyskując dwa przybliżenia I 1 i I 2, dokładniejszą całkę n Stanowi wyjście do metody Romberga