Metody rozwizywania ukadw rwna liniowych Par sw o

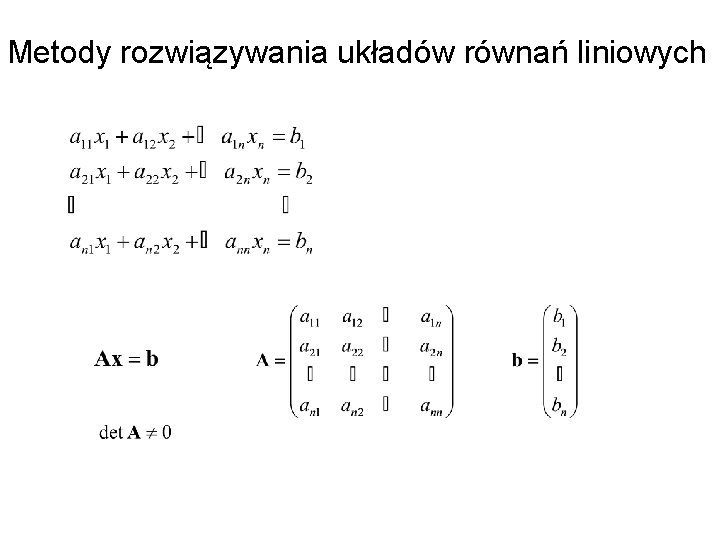
Metody rozwiązywania układów równań liniowych

Parę słów o macierzach Macierz m´n: tablica m na n (m wierszy n kolumn) liczb (np. tabliczka mnożenia). Macierz kwadradowa: m=n Macierz symetryczna (zawsze kwadratowa): aij=aji Macierz transponowana AT: (AT)ij=aji Macierz nieosobliwa: macierz o niezerowym wyznaczniku. Macierz dodatnio określona: x. TAx>0 dla każdego niezerowego wektora x. Norma euklidesowa macierzy: Norma spektralna macierzy Wskaźnik uwarunkowania macierzy

Metody skończone: • Metoda Gaussa-Jordana • Metody Choleskiego • Metoda Householdera • Metoda sprzężonych gradientów Metody iteracyjne dla dużych układów równań: • Metoda Jacobiego • Metoda Gaussa-Seidla

Metoda eliminacji Gaussa z wyborem elementu głównego w kolumnie Układ równań sprowadzamy do postaci trójkątnej Układ z macierzą trójkątną można następnie łatwo rozwiązać zaczynając od obliczenia wartości xn z n-tego równania, następnie wstawić xn do równania n-1 i wyliczyć z niego xn-1, następnie wstawić xn oraz xn-1 do równania n-2 i wyliczyć xn-2 aż do dotarcia do równania pierwszego i wyznaczenia x 1.

1. Wybieramy równanie i takie, że |ai 1| jest największym elementem w pierwszej kolumnie po czym przestawiamy i-te równanie na początek i eliminujemy x 1 z równań od 2 do n. 2. Procedurę powtarzamy z macierzą A(1) o rozmiarach (n-1)x(n-1) i wektorem b(1) o rozmiarze n-1, eliminując z nich drugą zmienną i otrzymując macierz A(2) o rozmiarach (n-2)x(n-2) i wektor b(2) o rozmiarze n-2. W ten sam sposób postępujemy z kolejnymi macierzami A(2), A(3), . . . , A(n-1) oraz wektorami b(2), b(3), . . . , b(n-1).

Dla j-tego kroku Po zakończeniu operacji otrzymujemy układ równań z macierzą trójkątną p jest liczbą przestawień wierszy macierzy A podczas sprowadzania układu równań do postaci trójkątnej.

3. Z otrzymanego układu równań z macierzą trójkątną wyznaczamy po kolei xn, xn-1, . . . , x 1. Wysiłek obliczeniowy (liczba mnożeń i dzieleń) w metodzie eliminacji Gaussa: Faktoryzacja macierzy A: n(n 2 -1)/3 operacji Przekształcenie wektora b: n(n-1)/2 operacji Obliczenie x: n(n+1)/2 operacji. Razem: n 3/3+n 2 -n/3≈n 3/3 operacji. Kod źródłowy metody eliminacji Gaussa.

Zastosowania metody eliminacji Gaussa i innych metod rozwiązywania układów równań liniowych. 1. Odwracanie macierzy Należy więc jednocześnie rozwiązać n układów równań z wektorami jednostkowymi poszczególnych osi w przestrzeni n-wymiarowej jako wyrazami wolnymi. Wszystkie wektory wyrazów wolnych przekształca się jednocześnie w czasie faktoryzacji macierzy A. Koszt obliczeniowy operacji wynosi (4/3)n 3 -n/3 operacji.

2. Mnożenie macierzy przez macierz odwrotną Jeżeli macierz A ma rozmiar nxn to macierz B musi mieć n wierszy (liczba kolumn może być dowolna, np. m). Zagadnienie sprowadza się do jednoczesnego rozwiązania m układów równań liniowych, których wektory wyrazów wolnych są równe kolejnym kolumnom macierzy B. Podobie jak przy odwracaniu macierzy podczas faktoryzacji A jednocześnie przekształcamy wszystkie kolumny macierzy B. Wysiłek obliczeniowy wynosi n 3/3 -n/3+mn 2 operacji.

Metoda Gaussa-Jordana W odróżnieniu od metody eliminacji Gaussa eliminujemy poszczególne zmienne nie tylko z równań następujących po danym równaniu ale również z równań je poprzedzających. W wyniku tej operacji końcowy układ równań ma postać diagonalną a w kroku j-1 ma on następującą postać:

Dla dużych n metoda Gaussa-Jordana wymaga ok. n 3/2 operacji.

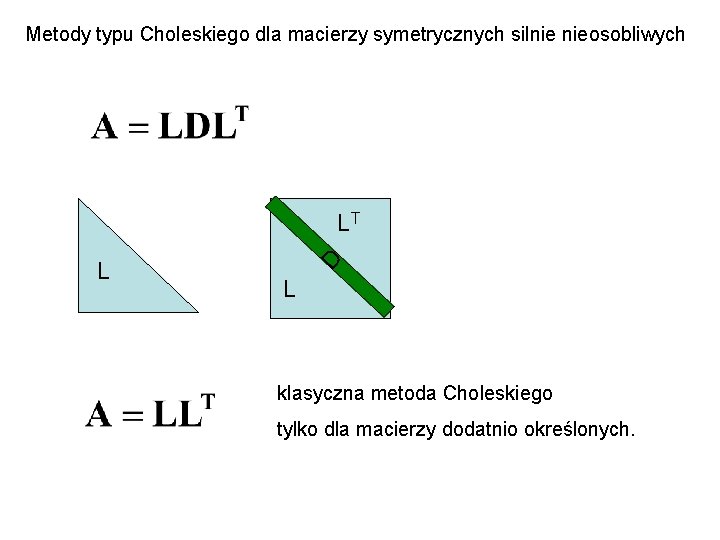
Metody typu Choleskiego dla macierzy symetrycznych silnie nieosobliwych L D LT L klasyczna metoda Choleskiego tylko dla macierzy dodatnio określonych.

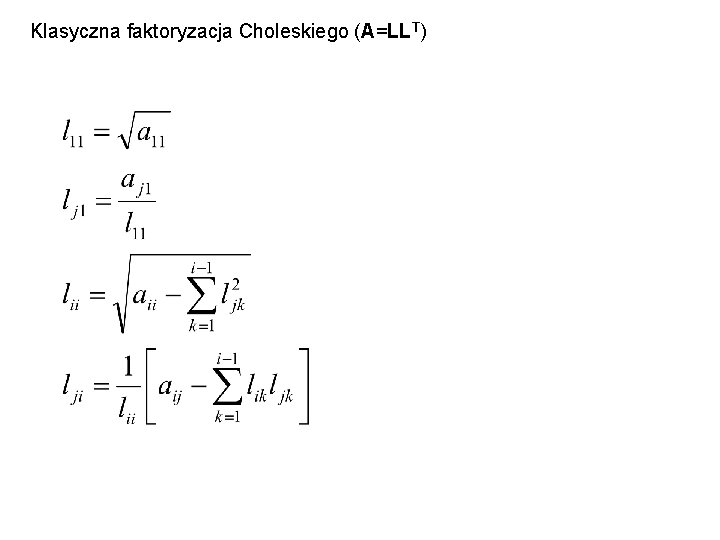
Postępowanie przy rozwiązywaniu układów równań metodą faktoryzacji Choleskiego. 1. Wyznaczenie faktorów L i D. Układ przyjmuje postać 2. LDLTx=b 3. 2. Obliczenie pomocniczego wektora w. 4. 5. w=L-1 b przez rozwiązanie układu równań Lw=b. Ponieważ L jest macierzą trójkątną dolną układ ten rozwiązuje się wyliczając kolejno w 1, w 2, …, wn podobnie jak w koncowym etapie eliminacji Gaussa. 6. 3. Obliczenie z=D-1 w (D jest macierzą diagonalną więc po prostu dzielimy wi przez dii. Ten etap nie występuje w klasycznej metodzie Choleskiego. 7. 4. Obliczenie x poprzez rozwiązanie układu równań z macierzą trójkątną górną 8. LTx=z 9. Ten etap jest identyczny z ostatnim etapem metody eliminacji Gaussa. 10. Metoda wymaga ok. n 3/6 operacji (2 razy mniej niż metoda eliminacji

Klasyczna faktoryzacja Choleskiego (A=LLT)

Faktoryzacja “bezpierwiastkowa” kod źródłowy

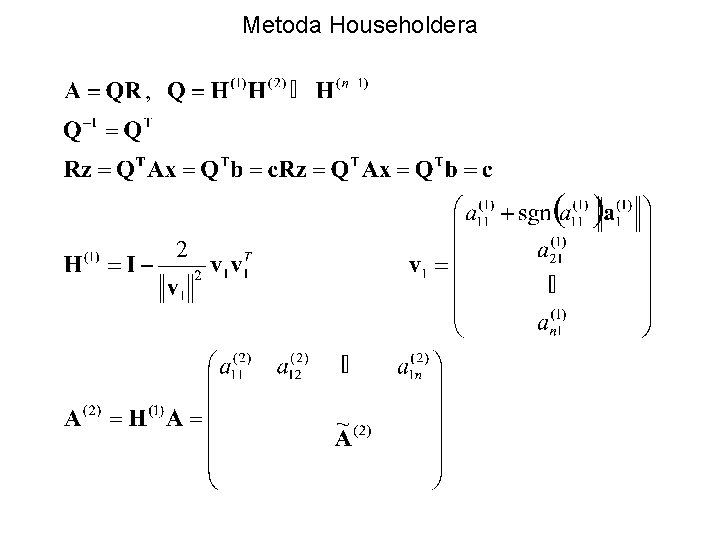
Metoda Householdera

Iteracyjna poprawa rozwiązania układu równań liniowych Proces kończymy gdy

Metoda sprzężonych gradientów Rozwiązanie układu równań przedstawiamy jako rozwiązanie zagadnienia minimalizacji funkcji E(x), której gradient jest różnicą pomiędzy lewą a prawą stroną układu równań. Metoda polega na wykonaniu n kroków w kierunkach d 0, d 1, …, dn-1 stopniowo zbliżających się do kierunku jednej z osi hiperparaboloidy E(x); długość kroku w każdym kierunku jest tak dobrana aby zlokalizować minimum E na tym właśnie kierunku. Poszczególne kierunki są Aortogonalne, tj. dk+1 Adk=0

1. Wybieramy punkt startowy x 0. Obliczamy d 0=-g 0=b-Ax 0. Jeżeli g 0=0 procedura jest zakończona. 2. W kroku k=0, 1, …, n-1 obliczamy Wstawiamy xk+1=xk+akdk Wstawiamy gk+1=gk+ak. Adk. Jeżeli ||gk+|||<e kończymy proces, w przeciwnym wypadku wstawiamy a następnie wstawiamy dk+1=-gk+1+bkdk Procedura jest teoretycznie zawsze zbieżna w n krokach (0, 1, …, n-1). Dla dobrze uwarunkowanego zadania zbieżność jest szybsza a dla źle uwarunkowanego zadania często występują oscylacje. Kod źródłowy metody sprzężonych gradientów.

Metody iteracji Jacobiego oraz iteracji Gaussa-Seidla Metody te stosuje się dla dużych układów równań, pojawiających się przykładowo przy rozwiązywaniu równań różniczkowych cząstkowych lub równań całkowych. Iteracja Jacobiego 1. Wyznaczamy przybliżenie początkowe x(0) 2. Kolejne przybliżenia x(1), x(2), …, obliczamy wyznaczając xi z i-tego równania dla i=1, 2, …, n a następnie podstawiając po prawej stronie poprzednie przybliżenie x. 3. Proces kończymy jeżeli ||x(p+1)-x(p)||<d.

Metoda iteracji Gaussa-Seidla. Metoda ta różni się od metody iteracji Jacobiego tym, że kolejne przybliżenie itej współrzędnej wektora x obliczamy wykorzystując przybliżenia x 1, …, xi-1 wyliczone w aktualnej iteracji oraz przybliżenia xi+1, …, xn z poprzedniej iteracji. Metoda iteracji Gaussa-Seidla jest zawsze zbieżna dla macierzy dodatnio określonych.

Optymalna wartość czynnika relaksacji; l 1 jest największą wartością własną macierzy B=B(l)+B(r) Wartość czynnika relaksacji łatwa do obliczenia. Kod źródłowy metody Gaussa-Seidla.