PREVIEWSUMMARY OF QUADRATIC EQUATIONS FUNCTIONS QUADRATIC means second

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS QUADRATIC – means second power Recall LINEAR – means first power

Click on the Quadratic Method you wish to review to go to those slides Factoring Method – Quick, but only works for some quadratic problems Square Roots of Both Sides – Easy, but only works when you can get in the form of (glob)2 = constant Complete the Square– Always works, but is recommended only when a = 1 or all terms are evenly divisible to set a to 1. Quadratic Formula – Always works, but be sure to rewrite in standard form first of ax 2 + bx + c = 0 How to Choose Among Methods 1 – 4? Summary & Hints Quadratic Functions – Summary of graphing parabolas from f(x) = ax 2 + bx + c form

METHOD 1 - FACTORING l l l Set equal to zero Factor Use the Zero Product Property to solve (Each factor with a variable in it could be equal to zero. )

METHOD 1 - FACTORING Any # of terms – Look for GCF factoring first! 1. 5 x 2 = 15 x 5 x 2 – 15 x = 0 5 x (x – 3) = 0 5 x = 0 OR x – 3 = 0 x = 0 OR x = 3 {0, 3}

METHOD 1 - FACTORING Binomials – Look for Difference of Squares 2. x 2 = 9 x 2 – 9 = 0 Conjugates (x + 3) (x – 3) = 0 x + 3 = 0 OR x – 3 = 0 x = – 3 OR x = 3 {– 3, 3}

METHOD 1 - FACTORING Trinomials – Look for PST (Perfect Square Trinomial) 3. x 2 – 8 x = – 16 x 2 – 8 x + 16 = 0 (x – 4) = 0 x – 4 = 0 OR x – 4 = 0 x = 4 OR x = 4 {4 d. r. } Double Root

METHOD 1 - FACTORING Trinomials – Look for Reverse of Foil 4. 2 x 3 – 15 x = 7 x 2 2 x 3 – 7 x 2 – 15 x = 0 (x) (2 x 2 – 7 x – 15) = 0 {-3/2, 0, 5} (x) (2 x + 3)(x – 5) = 0 x = 0 OR 2 x + 3 = 0 OR x – 5 = 0 x = 0 OR x = – 3/2 OR x = 5

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF METHOD 1: FACTORING Click here to return to menu slide

METHOD 2 – SQUARE ROOTS OF BOTH SIDES l l l Reorder terms IF needed Works whenever form is (glob)2 = c Take square roots of both sides (Remember you will need a l l sign!) Simplify the square root if needed Solve for x. (Isolate it. )

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 1. x 2 = 9 x= 3 {-3, 3} Note means both +3 and -3! x = -3 OR x = 3

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 2. x 2 = 18

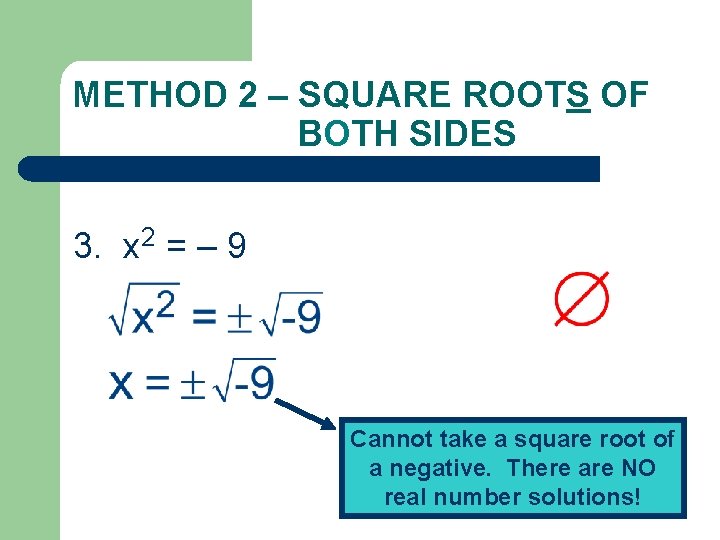
METHOD 2 – SQUARE ROOTS OF BOTH SIDES 3. x 2 = – 9 Cannot take a square root of a negative. There are NO real number solutions!

METHOD 2 – SQUARE ROOTS OF BOTH SIDES 4. (x-2)2 = 9 {-1, 5} This means: x = 2 + 3 and x = 2 – 3 x = 5 and x = – 1

METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 5. x 2 – 10 x + 25 = 9 (x – 5)2 = 9 x = 8 and x = 2 {2, 8}

METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 6. x 2 – 10 x + 25 = 48 (x – 5)2 = 48

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 1. x 2 = 121 x = 11 {-11, 11} Note means both +11 and -11! x = -11 OR x = 11

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 2. 2 x = – 81 Square root of a negative, so there are NO real number solutions!

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 3. 6 x 2 = 156 x 2 = 26

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 4. (a – 7)2 = 3

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES Rewrite as (glob)2 = c first if necessary. 5. 9(x 2 – 14 x + 49) = 4 (x – 7)2 = 4/9 {6⅓, 7⅔}

PRACTICE METHOD 2 – SQUARE ROOTS OF BOTH SIDES 6.

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF METHOD 2: SQUARE ROOTS OF BOTH SIDES Click here to return to menu slide

METHOD 3 – COMPLETE THE SQUARE • • • Goal is to get into the format: (glob)2 = c Method always works, but is only recommended when a = 1 or all the coefficients are divisible by a We will practice this method repeatedly and then it will keep getting easier!

METHOD 3 – COMPLETE THE SQUARE Example: 3 x 2 – 6 = x 2 + 12 x 2 x 2 – 12 x – 6 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 x 2 – 6 x – 3 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

METHOD 3 – COMPLETE THE SQUARE x 2 – 6 x – 3 = 0 x 2 – 6 x =3 Move constant to other side x 2 – 6 x + 9 = 3 + 9 Add (b/2)2 to both sides Leave space to replace it! This completes a PST! (x – 3)2 = 12 Rewrite as (glob)2 = c

METHOD 3 – COMPLETE THE SQUARE (x – 3)2 = 12 Take square roots of both sides – don’t forget Simplify Solve for x

PRACTICE METHOD 3 – COMPLETE THE SQUARE Example: 2 b 2 = 16 b + 6 2 b 2 – 16 b – 6 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 b 2 – 8 b – 3 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

PRACTICE METHOD 3 – COMPLETE THE SQUARE b 2 – 8 b – 3 = 0 b 2 – 8 b =3 b 2 – 8 b + 16 = 3 +16 Move constant to other side Leave space to replace it! Add (b/2)2 to both sides This completes a PST! (b – 4)2 = 19 Rewrite as (glob)2 = c

PRACTICE METHOD 3 – COMPLETE THE SQUARE (b – 4)2 = 19 Take square roots of both sides – don’t forget Simplify Solve for the variable

PRACTICE METHOD 3 – COMPLETE THE SQUARE Example: 3 n 2 + 19 n + 1 = n - 2 3 n 2 + 18 n + 3 = 0 Simplify and write in standard form: ax 2 + bx + c = 0 n 2 + 6 n + 1 = 0 Set a = 1 by division Note: in some problems a will already be equal to 1.

PRACTICE METHOD 3 – COMPLETE THE SQUARE n 2 + 6 n + 1 = 0 n 2 + 6 n = -1 Move constant to other side Leave space to replace it! n 2 + 6 n + 9 = -1 + 9 Add (b/2)2 to both sides This completes a PST! (n + 3)2 =8 Rewrite as (glob)2 = c

PRACTICE METHOD 3 – COMPLETE THE SQUARE (n + 3)2 = 8 Take square roots of both sides – don’t forget Simplify Solve for the variable

PRACTICE METHOD 3 – COMPLETE THE SQUARE What number “completes each square”? 1. x 2 – 10 x = -3 1. x 2 – 10 x + 25 = -3 + 25 2. x 2 + 14 x =1 2. x 2 + 14 x + 49 = 1 + 49 3. x 2 – 1 x =5 3. x 2 – 1 x + ¼ = 5 + ¼ 4. 2 x 2 – 40 x =4 4. x 2 – 20 x + 100 = 2 + 100

PRACTICE METHOD 3 – COMPLETE THE SQUARE Now rewrite as (glob)2 = c 1. x 2 – 10 x + 25 = -3 + 25 1. (x – 5)2 = 22 2. x 2 + 14 x + 49 = 1 + 49 2. (x + 7)2 = 50 3. x 2 – 1 x + ¼ = 5 + ¼ 3. (x – ½ )2 = 5 ¼ 4. x 2 – 20 x + 100 = 2 + 100 4. (x – 10)2 = 102

PRACTICE METHOD 3 – COMPLETE THE SQUARE Show all steps to solve. 2 ⅓k = 4 k k 2 = 12 k 2 k -⅔ -2 - 12 k =-2 k 2 - 12 k + 36 = - 2 + 36 (k - 6)2 = 34

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF METHOD 3: COMPLETE THE SQUARE Click here to return to menu slide

METHOD 4 – QUADRATIC FORMULA • This is a formula you will need to memorize! Works to solve all quadratic equations Rewrite in standard form in order to identify the values of a, b and c. Plug a, b & c into the formula and simplify! • QUADRATIC FORMULA: • • •

METHOD 4 – QUADRATIC FORMULA Use to solve: 3 x 2 – 6 = x 2 + 12 x Standard Form: 2 x 2 – 12 x – 6 = 0

METHOD 4 – QUADRATIC FORMULA

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. 2 2 x =x +6 2 2 x – 6 =0

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. 2 x +x +5=0

PRACTICE METHOD 4 – QUADRATIC FORMULA Show all steps to solve & simplify. x 2 +2 x - 4 = 0

THE DISCRIMINANT – MAKING PREDICTIONS b 2 – 4 ac is called the discriminant Four cases: 1. b 2 – 4 ac positive non-square two irrational roots 2. b 2 – 4 ac positive square two rational roots 3. b 2 – 4 ac zero one rational double root 4. b 2 – 4 ac negative no real roots

THE DISCRIMINANT – MAKING PREDICTIONS Use the discriminant to predict how many “roots” each equation will have. 1. x 2 – 7 x – 2 = 0 49– 4(1)(-2)=57 2 irrational roots 2. 0 = 2 x 2– 3 x + 1 9– 4(2)(1)=1 2 rational roots 3. 0 = 5 x 2 – 2 x + 3 4– 4(5)(3)=-56 no real roots 4. x 2 – 10 x + 25=0 100– 4(1)(25)=0 1 rational double root

THE DISCRIMINANT – MAKING PREDICTIONS about Parabolas The “zeros” of a function are the x-intercepts on it’s graph. Use the discriminant to predict how many x-intercepts each parabola will have and where the vertex is located. 1. y = 2 x 2 – x - 6 1– 4(2)(-6)=49 2 rational zeros opens up/vertex below x-axis/2 x-intercepts 2. f(x) = 2 x 2 – x + 6 1– 4(2)(6)=-47 no real zeros 3. y = -2 x 2– 9 x + 6 81– 4(-2)(6)=129 2 irrational zeros 4. f(x) = x 2 – 6 x + 9 opens up/vertex above x-axis/No x-intercepts opens down/vertex above x-axis/2 x-intercepts 36– 4(1)(9)=0 one rational zero opens up/vertex ON the x-axis/1 x-intercept

THE DISCRIMINANT – MAKING PREDICTIONS Note the proper terminology: The “zeros” of a function are the x-intercepts on it’s graph. Use the discriminant to predict how many x-intercepts each parabola will have. The “roots” of an equation are the x values that make the expression equal to zero. Equations have roots. Functions have zeros which are the x-intercepts on it’s graph.

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF METHOD 4: QUADRATIC FORMULA Click here to return to menu slide

FOUR METHODS – HOW DO I CHOOSE? Some suggestions: Quadratic Formula – works for all quadratic equations, but look first for a “quicker” method. Don’t forget to simplify square roots and use value of discriminant to predict number of roots. Square Roots of Both Sides – use when the problem is easily written as glob 2 = constant. Examples: 3(x + 2)2=12 or x 2 – 75 = 0

FOUR METHODS – HOW DO I CHOOSE? Some suggestions: Factoring – doesn’t always work, but IF you see the factors, this is probably the quickest method. Examples: x 2 – 8 x = 0 has a GCF 4 x 2 – 12 x + 9 = 0 is a PST x 2 – x – 6 = 0 is easy to FOIL Complete the Square – best used when a = 1 and b is even (so you won’t need to use fractions). Examples: x 2 – 6 x + 1 = 0

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF HOW TO CHOOSE A QUADRATIC METHOD Click here to return to menu slide

REVIEW – QUADRATIC FUNCTIONS a. The graph is a parabola. Opens up if a > 0 and down if a < 0. b. To find x-intercepts: – may have Zero, One or Two x-intercepts 1. Set y or "f(x)" to zero on one side of the equation 2. Factor & use the Zero Product Prop to find TWO x-intercepts c. To find y-intercept, set x = 0. Note f(0) will equal c. I. E. (0, c) d. To find the coordinates of the vertex (turning pt): 1. x-coordinate of the vertex comes from this formula: 2. plug that x-value into the function to find the y-coordinate e. The axis of symmetry is the vertical line through vertex: x =

REVIEW – QUADRATIC FUNCTIONS Example Problem: f(x) = x 2 – 2 x – 8 a. Opens UP since a = 1 (that is, positive) b. x-intercepts: 0 = x 2 – 2 x – 8 0 = (x – 4)(x + 2) (4, 0) and (– 2, 0) c. y-intercept: f(0) = (0)2 – 2(0) – 8 (0, – 8) d. vertex: e. axis of symmetry: x = 1

PREVIEW/SUMMARY OF QUADRATIC EQUATIONS & FUNCTIONS END OF ENTIRE SLIDE SHOW Click here to return to menu slide