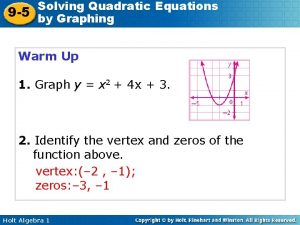
9 3 SOLVING QUADRATIC EQUATIONS Quadratic Equation A

9. 3: SOLVING QUADRATIC EQUATIONS: Quadratic Equation: A function that can be written in the form ax 2+bx+c = 0 where a ≠ 0. Standard Form of a Quadratic: A function written in descending degree order, that is ax 2+bx+c = 0.

Roots of an equation: the solution of a quadratic equation, the x-intercepts of the graph. Zeros of the function: The x-intercepts of the graph.

GOAL:

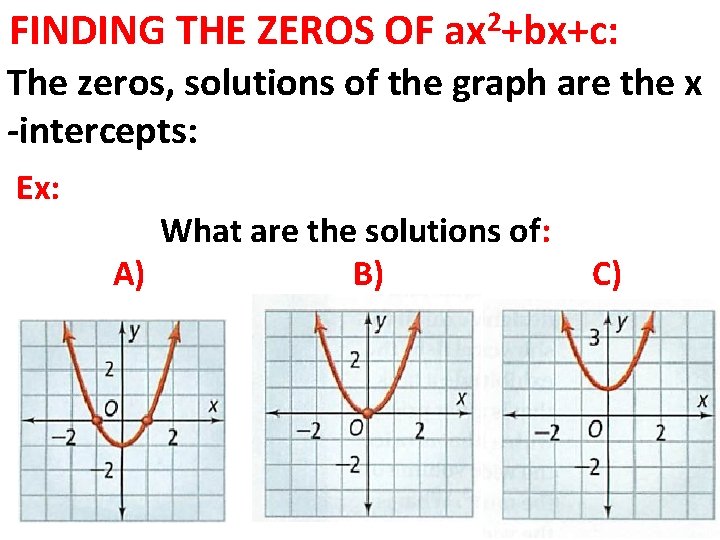
FINDING THE ZEROS OF 2 ax +bx+c: The zeros, solutions of the graph are the x -intercepts: Ex: What are the solutions of: A) B) C)

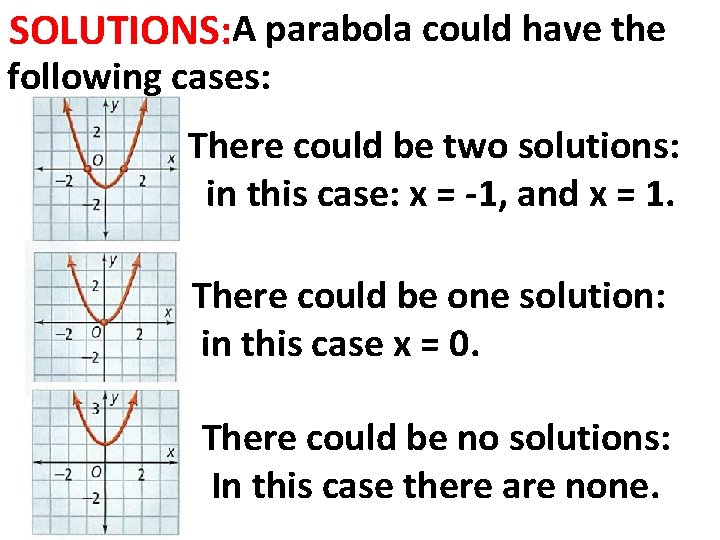
SOLUTIONS: A parabola could have the following cases: There could be two solutions: in this case: x = -1, and x = 1. There could be one solution: in this case x = 0. There could be no solutions: In this case there are none.

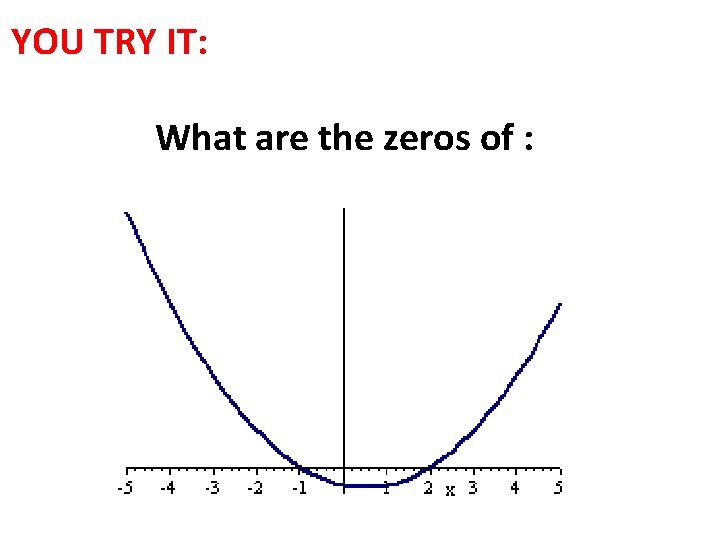
YOU TRY IT: What are the zeros of :

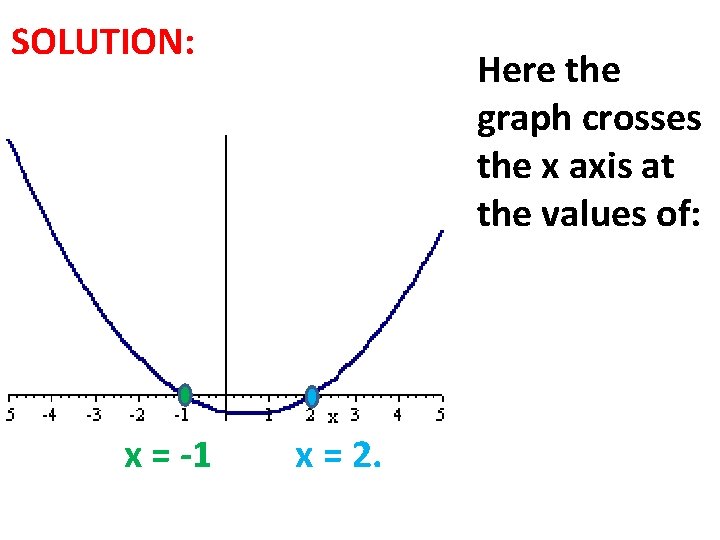
SOLUTION: x = -1 Here the graph crosses the x axis at the values of: x = 2.

FINDING THE ZEROS OF 2 ax + c = 0: When the equation does not include the bx term, we use SQUARE ROOTS: Ex: What are the solutions of: A) m 2 – 36 = 0 B) 3 x 2+15 = 0 C) 4 d 2+16 = 32

SOLUTIONS: To find the x-intercepts, we must solve for the variable: A) m 2 – 36 = 0 m 2 = 36 m = -6, +6 B) 3 x 2+15 = 0 3 x 2 = -15 x 2 = -5 No solution C) 4 d 2+16 2=0 4 d = 16 d 2 = 0 d=0

REAL-WORLD: You have enough paint to cover an area of 50 ft 2. What is the side length of the largest square that you could paint? Round your answer to the nearest tenth of a foot.

SOLUTION: The area of a square is (side) = s 2 Paint covers at most 50 ft 2 Then: s 2= 50 ft 2 Notice that length cannot be negative thus s = 7. 1 ft

VIDEOS: Quadratic Graphs and Their Properties Solving Quadratics: http: //www. khanacademy. org/math/trigonometry/polyn omial_and_rational/quad_formula_tutorial/v/solvingquadratic-equations-by-square-roots

CLASSWORK: Page 550 -551: Problems: 1, 2, 3, 4, 6, 8, 10, 13, 22, 29, 31, 32, 36, 42.