Unit 18 QUADRATIC EQUATIONS 1 QUADRATIC EQUATIONS A














- Slides: 14

Unit 18 QUADRATIC EQUATIONS 1

QUADRATIC EQUATIONS ¢ ¢ ¢ A quadratic equation with one variable has at least one term raised to the second power with no terms of a higher power A quadratic equation that does not contain a first power variable (x term) is called an incomplete or pure quadratic equation Examples: l l 2 Quadratic equation: 4 x 2 + x = 9 Pure quadratic equation: y 2 = 2

QUADRATIC EQUATIONS ¢ The general form of a quadratic equation is ax 2 + bx + c = 0 a is the coefficient of the x 2 term and cannot equal 0 l b is the coefficient of the x term l c is the constant term that does not contain x in any form l 3

INCOMPLETE QUADRATIC EQUATIONS ¢ Procedure for solving incomplete quadratic equations: Isolate the term containing x 2 on one side of the equation l If x 2 has a coefficient other than 1, divide both sides of the equation by the coefficient l Take the square root of both sides of the equation. Write a ± sign before the square root quantity l Check both roots in the original equation l 4

SOLVING AN INCOMPLETE QUADRATIC EQUATION ¢ Solve for x: 7 x 2 = 651 l Divide both sides of the equation by 7: x 2 = 93 l Square root both sides of the equation: 5 Note: The answer has been rounded. Both answers 9. 644 and – 9. 644 should be checked in the original equation.

PRACTICAL APPLICATION EXAMPLE ¢ Determine the radius of a circle given that its area is 65 square inches l l The area of a circle is times the radius squared or: A = r 2 Substituting 65 square inches for the area gives us: 65 in 2 = r 2 Now, solving for r: 20. 69 in 2 = r 2 4. 55 in = r The negative answer is discarded, leaving 4. 55 inches Ans 6

COMPLETE QUADRATIC EQUATIONS A quadratic equation that contains both the second power variable (x 2 term) and the first power variable (x term) is called a complete quadratic equation ¢ Different methods that can be used to solve quadratic equations ¢ The quadratic formula will be the method used here ¢ 7

THE QUADRATIC FORMULA ¢ 8 If the general quadratic equation (ax 2 + bx + c = 0) is transformed and solved for x, the resulting equation is called the quadratic formula:

USING THE QUADRATIC FORMULA 9 ¢ Solve 2 x 2 + 3 x – 2 = 0 using the quadratic formula. l Identify a, b, and c. In this equation a = 2, b = 3, and c = – 2. l Substituting these values into the quadratic formula: ¢ Simplify: ¢ Find both solutions:

PRACTICAL APPLICATION EXAMPLE ¢ Find the length and width of a rectangle with an area of 24 in 2 given that its length is two inches greater than its width l l l Let x = the width; then the length = x + 2…(remember area=l*w) Rearrange the equation and find a, b, and c • x 2 + 2 x – 24 = 0; so a = 1, b = 2, and c = – 24 Solve for x using the quadratic formula. Not possible 10 Width = 4 in. length = x + 2 or 6 in. Ans

PRACTICE PROBLEMS ¢ Solve problems 1– 4. Round to the nearest hundredth whenever necessary: 1. 8 x 2 = 94 2. 3. 4. 11 7. 6 y 2 – 29. 5 = 0 3 x 2 – 9 = x 2 + 4 Find the radius of a circle given that the area is 49. 6 square inches. The area of a circle is figured by A=3. 14 r 2. Where A is the area and r is your radius. Round your answer to the nearest hundredth of an inch.

PRACTICE PROBLEMS (Cont) Given that power (P) is equal to current (I) squared times resistance (R). Find the current if the power is 50 watts and the resistance is 15 ohms. Round the answer to the nearest hundredth of an ampere. Note: An ampere (A) is the unit measure of current. Use the quadratic formula to solve problems 6– 8: 6. 6 x 2 + 5 x – 6 = 0 7. 9 y 2 – 18 y = – 8 8. x 2 – x = 6 5. ¢ 12

PRACTICE PROBLEMS (Cont) Given the equation for the free fall of an object (like a parachuter) s = vot + 1/2 at 2; find t (time in seconds) when s = 50, a = 32, and vo = 4. Round to the nearest hundredth of a second 10. Given that the area of a parallelogram is base times height. Find the base and height of a parallelogram with an area of 18 square inches and a height that is 3 inches longer than the base 9. 13

PROBLEM ANSWER KEY ± 3. 43 2. ± 1. 97 3. ± 2. 55 4. 3. 97 inches 5. 1. 83 A 6. – 3/2 and 2/3 7. 2/3 and 4/3 8. – 2 and 3 9. 1. 65 seconds 10. base = 3” and the height = 6” 1. 14
 Unit 4 lesson 4 factoring to solve quadratic equations
Unit 4 lesson 4 factoring to solve quadratic equations Unit 6 review questions
Unit 6 review questions Quadratic quadratic systems examples
Quadratic quadratic systems examples Example of quadratic formula
Example of quadratic formula Discriminant equation
Discriminant equation The area of a rectangular fountain is (x^2+12x+20)
The area of a rectangular fountain is (x^2+12x+20) Quadratic equation
Quadratic equation Square root method for solving quadratic equations
Square root method for solving quadratic equations Zero product property quadratic equations
Zero product property quadratic equations Factoring steps
Factoring steps 5-3 solving quadratic equations by factoring
5-3 solving quadratic equations by factoring 9-7 solving quadratic equations by using square roots
9-7 solving quadratic equations by using square roots 9-6 solving quadratic equations by factoring
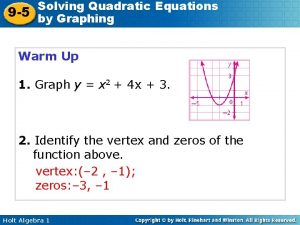
9-6 solving quadratic equations by factoring 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing 9-5 solving quadratic equations by graphing
9-5 solving quadratic equations by graphing