Section 11 1 Quadratic Equations Quadratic Equations The




















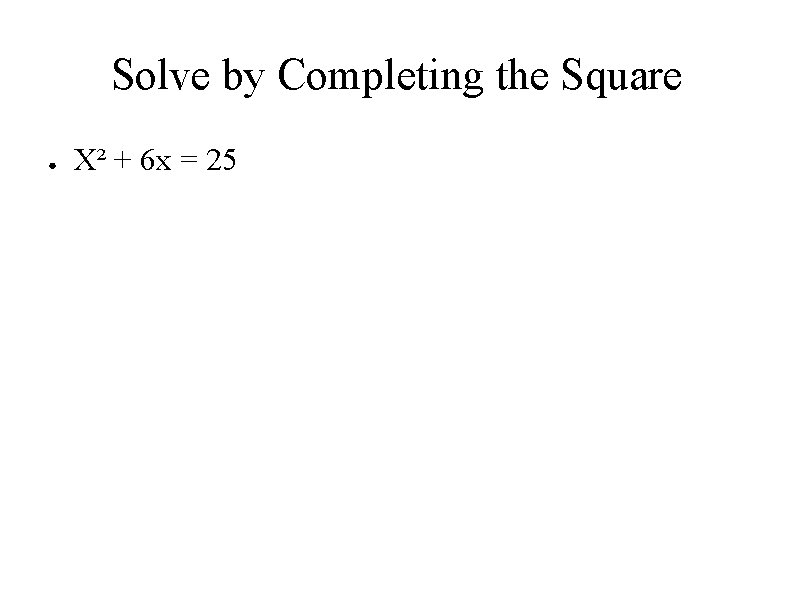
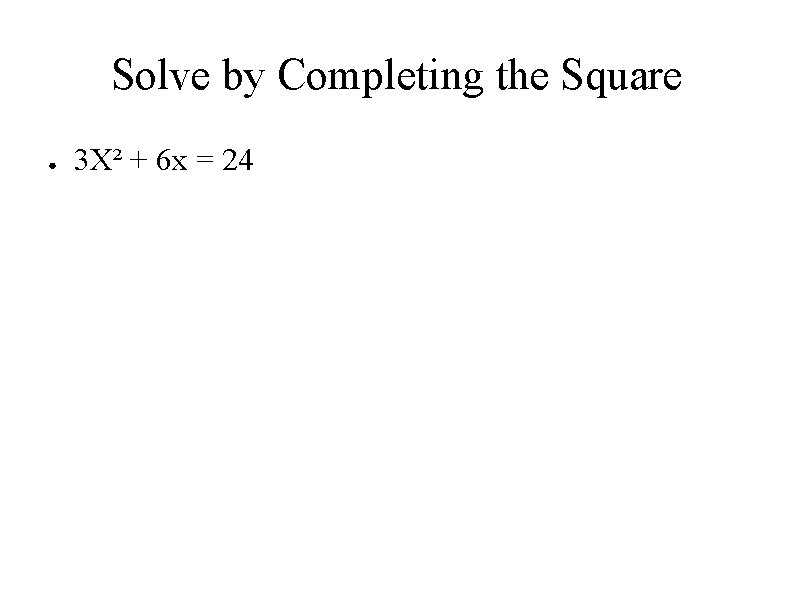

- Slides: 23

Section 11. 1 Quadratic Equations

Quadratic Equations ● ● The general form of the quadratic equation is ax² + bx + c = 0 where a ≠ 0 The unique quadratic equation forms are – ax² + bx + c = 0 – ax² + bx = 0 – ax² + c = 0 OR ax² - c = 0

Zero Product Property ● Zero Product Rule – ● If ab = 0 the a = 0 or b = 0 Theory – How can you create a zero through multiplication? ● 0*0 ● #*0 ● 0*#

How to solve ax² + bx = 0 ● Given – ● Factor the Greatest Common Factor – ● x=0 OR ax + b = 0 Solve each equation – ● x(ax + b) = 0 Use the zero product property – ● ax² + bx = 0 x=0 OR Check your answers x = -b/a

Example ● ● Solve 2 x² – 3 = 29 – 2 x² = 29 +3 – 2 x² = 32 – x² = 16 – x = 4 OR x = -4 Check – x=4 2(4)² – 3 = 29 29=29 – x = -4 2(-4)² – 3 = 29 29=29

Example ● Solve x² – 1 = 15

Example ● Solve x² + 5 = 10

Square Root Property ● ● Square Root Property – For any real number k, if x² = k, the – x = √k – x = ± √k or x = -√k Theory – Let us factor this problem. – x² – 4 = 0 – x– 2=0 – x=2 (x – 2)(x + 2) = 0 OR OR x+2=0 x = -2

How to solve ax² - c = 0 ● Given – ● Move the constant to the other side – ● x² = c/a Use the square root property – ● ax² = c Divide both sides by the coefficient – ● ax² - c = 0 X = √c/a Check the solutions or -√c/a


Example ● Solve 2 x² = 18

Example ● Solve -x² = 25

Example ● Solve 2 x² = 18

How to solve ax² + bx + c = 0 ● There are three ways to solve this problem – Factoring (5. 7) – Completing the square (11. 2) – Quadratic Formula (11. 2)

Completing the square ● ● Completing the square takes the quadratic equation and turns it into a perfect square trinomial. Then you isolate the variable by using the square root property.

Perfect Square Trinomial ● ● Perfect Square trinomial – x² + 2 xb + b² = (x + b)² – x² - 2 xb + b² = (x - b)² We will be creating a perfect square trinomial – We will start with the x² - 2 xb – We will create third term – We will then factor the perfect square trinomial

Examples of making the third term ● Find the constant for x² + 2 x ● Find the constant for x² + 4 x ● Find the constant for x² + 12 x ● Find the constant for x² – 8 x ● Find the constant for x² + 21 x

Generic Third Term ● Can you find a pattern to create third term or new constant?

Steps ● Write equation in decreasing order ● Move constant to the other side ● Divide both sides by the leading coefficient ● Find the new constant – C = [(1/2)b]² ● Add the new constant to both sides ● Factor one side, simplify the other ● Use the square root property ● Isolate the variable

Solve by Completing the Square ● 2 x² + 8 x + 3 = 0 ● 2 x² + 8 x = -3 ● x² + 4 x = -3/4 – New C = [(1/2)(4)]² = 4 ● x² + 4 x + 4 = -3/4 + 4 ● (x+2)² = 13/4 ● X+2 = ±√(13/4) ● X+2 = ±√ 13 / 2 ● X = -2 ±√ 13 / 2
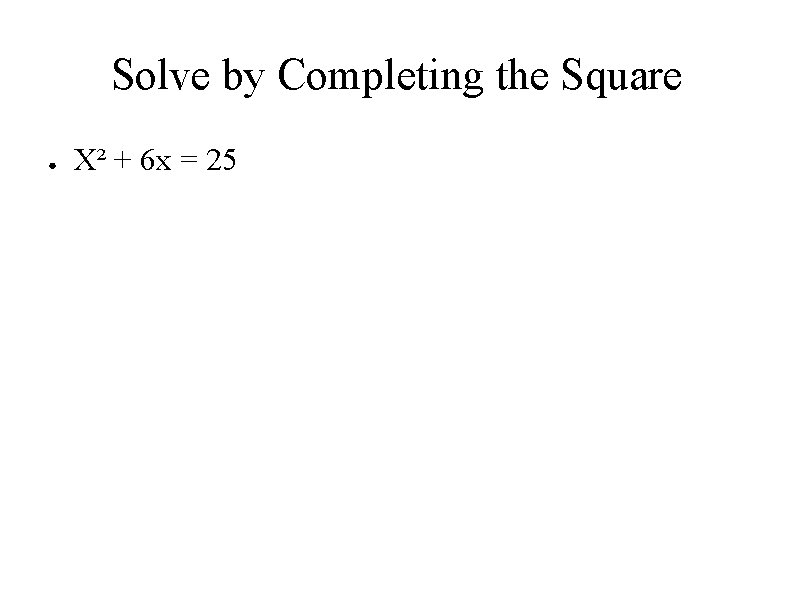
Solve by Completing the Square ● X² + 6 x = 25
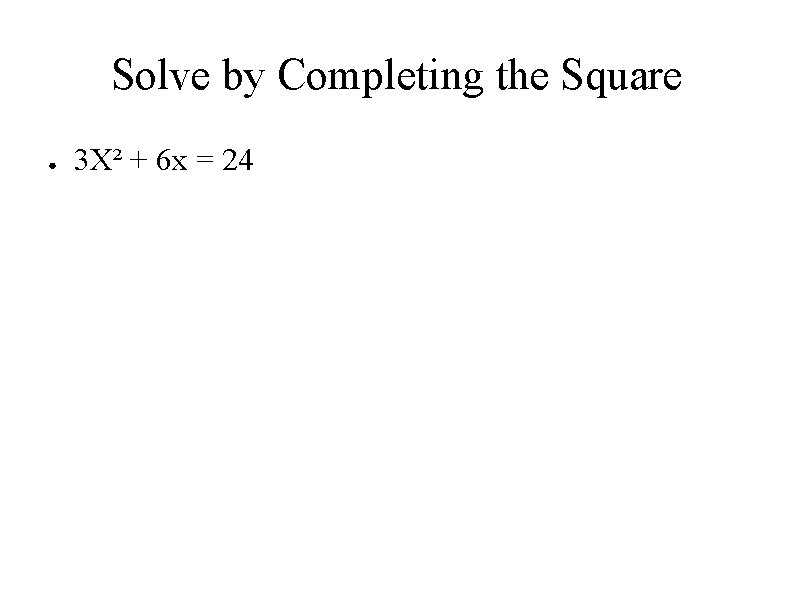
Solve by Completing the Square ● 3 X² + 6 x = 24

Homework ● 11. 1 – # 10, 11, 24, 39 -50, 51, 53, 55, 57
 Section 5 topic 3 solving quadratic equations by factoring
Section 5 topic 3 solving quadratic equations by factoring Section 5 topic 3 solving quadratic equations by factoring
Section 5 topic 3 solving quadratic equations by factoring Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worms-breton
Tư thế worms-breton Chúa sống lại
Chúa sống lại Các môn thể thao bắt đầu bằng từ đua
Các môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân 101012 bằng
101012 bằng Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ