Quadratic Equations Concepts 1 Solve Quadratic Equations by

Quadratic Equations

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Solve Quadratic Equations by Using the Zero Product Property If mn = 0, then m = 0 or n = 0

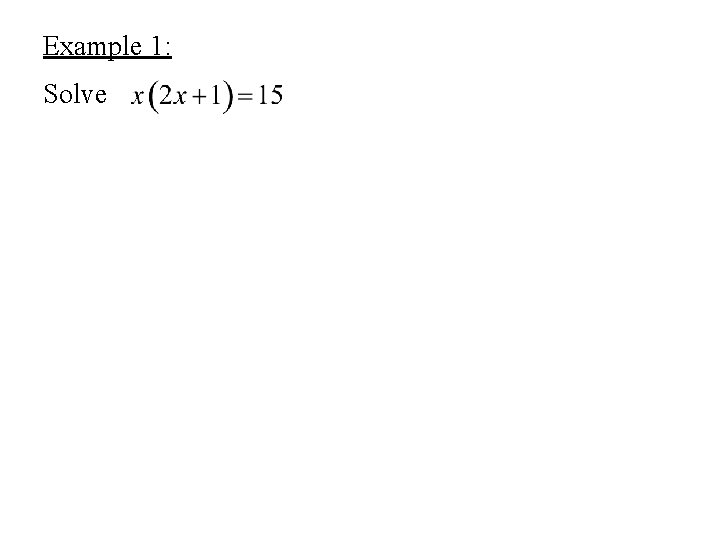
Example 1: Solve

Example 2: Solve

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Solve Quadratic Equations by Using the Square Root Property

Example 3: Solve

Example 4: Solve

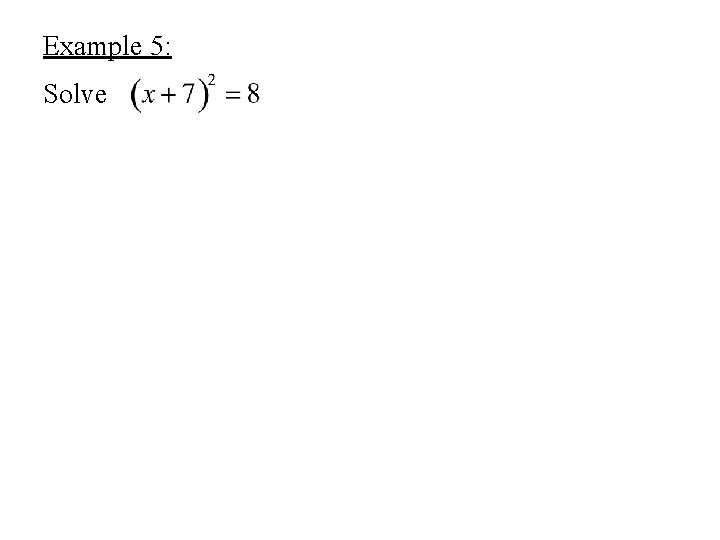
Example 5: Solve

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Complete the Square Step 1 Divide both sides by a to make the leading coefficient 1. Step 2 Isolate the variable terms on one side of the equation. Step 3 Complete the square. Add the square of one-half the linear term coefficient to both sides. Factor. Step 4 Apply the square root property and solve for x.

Example 6: Solve Step 1 Step 2 Step 3 Step 4

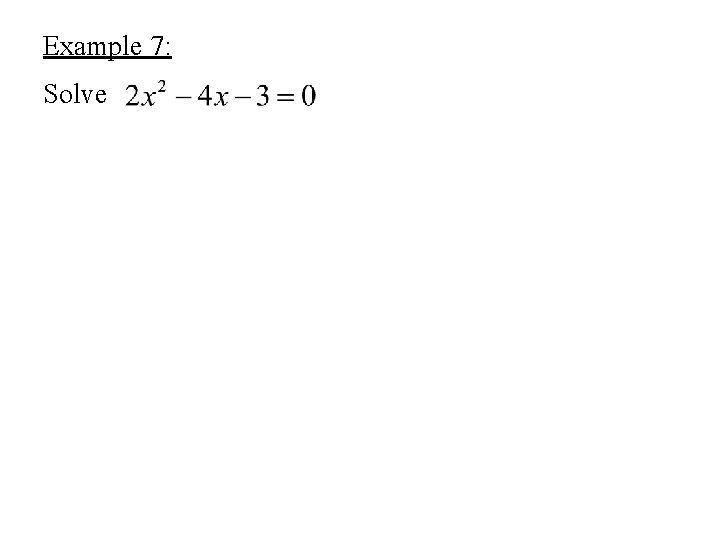
Example 7: Solve

Example 8: Solve

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Solve Quadratic Equations by Using the Quadratic Formula

Example 9: Solve

Example 9 continued: Solve (compare to completing the square)

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Use the Discriminant is called the discriminant.

Use the Discriminant is zero � 1 real solution

Use the Discriminant is positive � 2 real solutions

Use the Discriminant is negative � 2 imaginary solutions

Concepts 1. Solve Quadratic Equations by Using the Zero Product Property 2. Solve Quadratic Equations by Using the Square Root Property 3. Complete the Square 4. Solve Quadratic Equations by Using the Quadratic Formula 5. Use the Discriminant 6. Solve an Equation for a Specified Variable

Example 10: Solve for a

Example 11: Solve for x

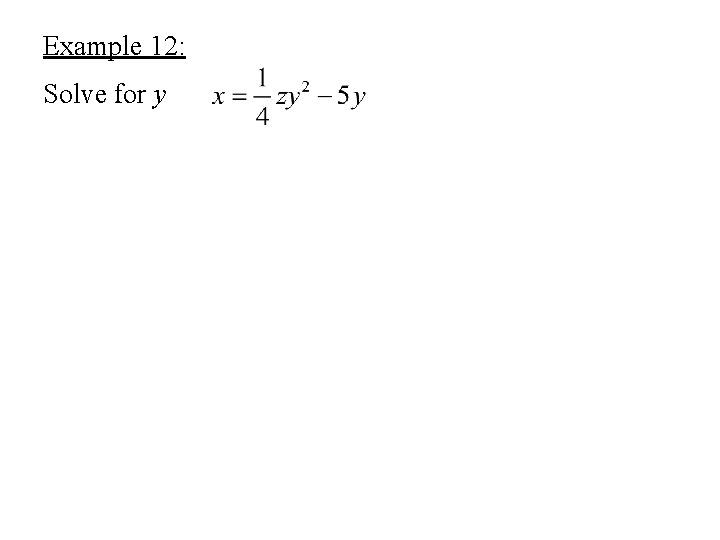
Example 12: Solve for y

Example 12 continued: