Solving Quadratic Equations Objective SWBAT solve quadratic equations

Solving Quadratic Equations Objective: SWBAT solve quadratic equations and systems, and determine roots of a higher order polynomial

Warm Up Factor the polynomial. 1. x 2 – 49 2. x 2 + 6 x + 5 3. 3 x 2 +10 x – 8 4. 3 x 2 -24 5. 8 x 2 + 38 x -10

Quadratic Equations A Quadratic Equation is written in the form: ax 2 + bx + c = 0 where a ≠ 0, and a, b, c represent real numbers. • This form is called standard form • “Second degree equation”

Methods Used to Solve Quadratic Equations 1. Graphing 2. Factoring 3. Square Root Property 4. Completing the Square 5. Quadratic Formula

Why so many methods? - Some methods will not work for all equations. - Some equations are much easier to solve using a particular method. - Variety is the spice of life.

Graphing � Graphing to solve quadratic equations does not always produce an accurate result. � If the solutions to the quadratic equation are irrational or complex, there is no way to tell what the exact solutions are by looking at a graph. � Graphing is very useful when solving contextual problems involving quadratic equations. � We are NOT going to focus on graphing in this course because of these reasons

Factoring � Factoring is typically one of the easiest and quickest ways to solve quadratic equations; HOWEVER… not all quadratic polynomials can be factored! � This means that factoring will not work to solve many quadratic equations.

Factor: 2 1. x – 24 = 0 (x + 4)(x – 6) = 0 x+4=0 x– 6=0 x=– 4 x=6
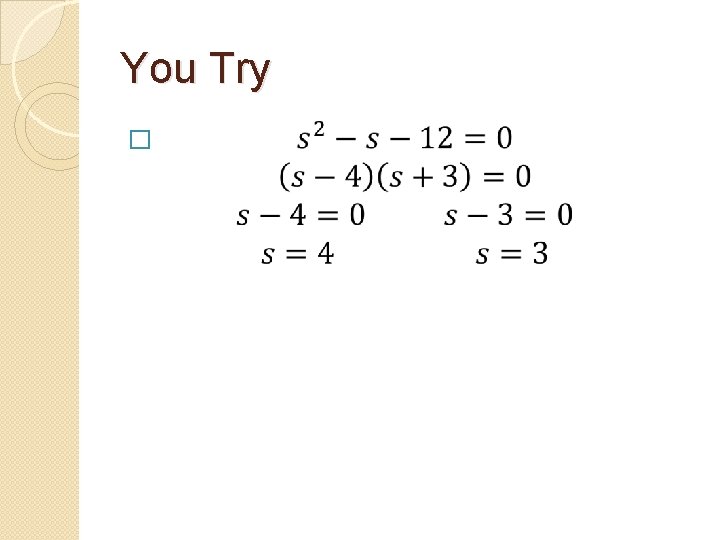
You Try �

Square Root Property � This method is also relatively quick and easy; HOWEVER… it only works for equations in which the quadratic polynomial is written in the following form: 2 2 x = n or (x + c) = n

Square Root Property Example: 2 1. x = 49 x=± 7

Square Root Property Example: 2 2. (x + 3) = 25 x+3=± 5 x+3=5 x=2 x + 3 = – 5 x = – 8

Homework Day 1 �Textbook Pages 440 -441 ◦ # 29, 30, 31, 33, 37, 39, 46
- Slides: 13