ALGEBRA 2 Section 5 3 Solving Quadratic Equations

ALGEBRA 2 Section 5. 3 Solving Quadratic Equations by Graphing and Factoring

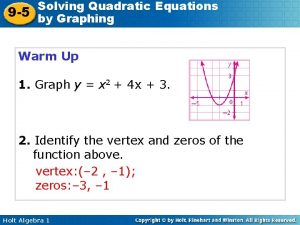
Zero(s) of a Function • • • When y = 0 x-intercepts Where the graph hits the x-axis Solutions 0 = ax 2 + bx + c 2 Solutions 1 Solution No Solutions

Symmetry • Zeros are symmetric about the axis of symmetry • Can find the h value by averaging the zeros

Use a graph or table to find the x-intercepts. A) By hand 1) Find the vertex and y-intercept 2) Make a table just like in sect 2 3) Use table or graph to estimate the xintercepts B) Can use a calculator to graph and estimate xintercepts (Must sketch graph for me to see!!!)

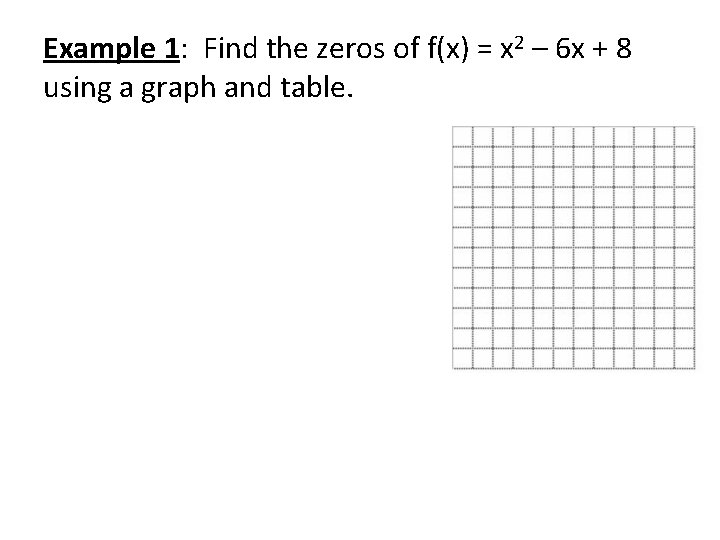
Example 1: Find the zeros of f(x) = x 2 – 6 x + 8 using a graph and table.

Use Factoring to Solve • Solve a Quadratic means finding the zeros • 0 = ax 2 + bx + c • Zero Product Property – When ab = 0, a = 0 or b = 0 • Solve by factoring – Factor Quadratic – Set each binomial = 0 – Solve each – These are your x-intercepts f(x) = x 2 – 5 x – 6

Example 2: Find the zeros of each function by factoring. A) f(x) = x 2 – 4 x – 12 B) g(x) = 3 x 2 + 18 x

Height Over Time Applications • As a ball is thrown in the air, gravity pulls it back down • If we graph its height over time, we get a parabola • h = -½gt 2 + v 0 t + h 0 – h = height at t seconds – g = gravity – v 0 = “v naught” = initial velocity = starting speed – h 0 = “h naught” = initial height • Gravity on Earth = 32 ft/sec 2 = 9. 8 m/sec 2 • Height Quadratics – h (in feet) = -16 t 2 + v 0 t + h 0 – h (in meters) = -4. 9 t 2 + v 0 t + h 0 No Air Resistance, No Wind, or Terminal Velocity

h = -16 t 2 + 20 t +5 • Height is in feet h (0. 6, 11. 2) • Initial velocity = 20 ft/sec • Initial height = 5 feet • Vertex = Max height (0. 6 sec, 11. 2 ft) • x-intercept: when it hits the ground: when height =0 1. 5 sec & -0. 2 sec (0, 5) (1. 5, 0) count by 0. 5’s on the x-axis t

Example 3: A golf ball is hit from ground level with an initial vertical velocity of 80 ft/s. After how many seconds will the ball hit the ground?

Quadratic Expressions • Can have one term = monomial 4 x 2 • Can have two terms = binomial 4 x 2 + 8 x • Can have three terms = trinomial 4 x 2 + 8 x - 24

2 Special Cases Expand (2 x + 3) (2 x – 3) Factoring 9 x 2 – 25 (2 x + 3)2 9 x 2 – 30 x + 25

Example 4: Find the roots of each equation by factoring. A) 4 x 2 = 25 B) 18 x 2 = 48 x – 32

Example 5: Write a quadratic function(rule) in standard form with zeros 4 and -7. 1) Write equations as factors. 2) FOIL

Assignment #3: Page 338 #’s 18 -46, (80)