Solving Quadratic Equations 8 6 by Factoring Warm

Solving Quadratic Equations 8 -6 by Factoring Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 1 Algebra 11 Holt Mc. Dougal

Solving Quadratic Equations 8 -6 by Factoring Warm Up Find each product. 1. (x + 2)(x + 7) 2. (x – 11)(x + 5) x 2 + 9 x + 14 x 2 – 6 x – 55 3. (x – 10)2 x 2 – 20 x + 100 Factor each polynomial. (x + 5)(x + 7) 4. x 2 + 12 x + 35 (x – 7)(x + 9) 5. x 2 + 2 x – 63 6. x 2 – 10 x + 16 (x – 2)(x – 8) 7. 2 x 2 – 16 x + 32 2(x – 4)2 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Objective Solve quadratic equations by factoring. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring You have solved quadratic equations by graphing. Another method used to solve quadratic equations is to factor and use the Zero Product Property. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 1 A: Use the Zero Product Property to solve the equation. Check your answer. (x – 7)(x + 2) = 0 x – 7 = 0 or x + 2 = 0 x = 7 or x = – 2 The solutions are 7 and – 2. Holt Mc. Dougal Algebra 1 Use the Zero Product Property. Solve each equation.

Solving Quadratic Equations 8 -6 by Factoring Example 1 A Continued Use the Zero Product Property to solve the equation. Check your answer. Check (x – 7)(x + 2) = 0 (7 – 7)(7 + 2) (0)(9) 0 Check (x – 7)(x + 2) = (– 2 – 7)(– 2 + 2) (– 9)(0) 0 Holt Mc. Dougal Algebra 1 0 0 0 0 Substitute each solution for x into the original equation.

Solving Quadratic Equations 8 -6 by Factoring Example 1 B: Use the Zero Product Property to solve each equation. Check your answer. (x – 2)(x) = 0 (x)(x – 2) = 0 x = 0 or x – 2 = 0 x=2 The solutions are 0 and 2. Check (x – 2)(x) = 0 (0 – 2)(0) (– 2)(0) 0 Holt Mc. Dougal Algebra 1 Use the Zero Product Property. Solve the second equation. (x – 2)(x) = 0 Substitute each (2 – 2)(2) 0 solution for x into (0)(2) 0 the original 0 0 equation. 0 0 0

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 1 a Use the Zero Product Property to solve each equation. Check your answer. (x)(x + 4) = 0 x = 0 or x + 4 = 0 x = – 4 The solutions are 0 and – 4. Check (x)(x + 4) = 0 (0)(0 + 4) (0)(4) 0 Holt Mc. Dougal Algebra 1 Use the Zero Product Property. Solve the second equation. (x)(x +4) = 0 Substitute each (– 4)(– 4 + 4) 0 solution for x into (– 4)(0) 0 the original 0 0 equation. 0 0 0

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 1 b Use the Zero Product Property to solve the equation. Check your answer. (x + 4)(x – 3) = 0 x + 4 = 0 or x – 3 = 0 x = – 4 or x=3 The solutions are – 4 and 3. Holt Mc. Dougal Algebra 1 Use the Zero Product Property. Solve each equation.

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 1 b Continued Use the Zero Product Property to solve the equation. Check your answer. (x + 4)(x – 3) = 0 Check (x + 4)(x – 3 ) = 0 (– 4 + 4)(– 4 – 3) 0 (0)(– 7) 0 0 0 Check (x + 4)(x – 3 ) = 0 (3 + 4)(3 – 3) (7)(0) 0 Holt Mc. Dougal Algebra 1 0 0 0 Substitute each solution for x into the original equation.

Solving Quadratic Equations 8 -6 by Factoring If a quadratic equation is written in standard form, ax 2 + bx + c = 0, then to solve the equation, you may need to factor before using the Zero Product Property. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Helpful Hint To review factoring techniques, see lessons 8 -3 through 8 -5. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 2 A: Solving Quadratic Equations by Factoring Solve the quadratic equation by factoring. Check your answer. x 2 – 6 x + 8 = 0 (x – 4)(x – 2) = 0 Factor the trinomial. x – 4 = 0 or x – 2 = 0 Use the Zero Product Property. x = 4 or x = 2 Solve each equation. The solutions are 4 and 2. Check x 2 – 6 x + 8 = 0 (4)2 – 6(4) + 8 0 (2)2 – 6(2) + 8 0 16 – 24 + 8 0 4 – 12 + 8 0 0 0 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 2 B: Solving Quadratic Equations by Factoring Solve the quadratic equation by factoring. Check your answer. x 2 + 4 x = 21 – 21 x 2 + 4 x – 21 = 0 The equation must be written in standard form. So subtract 21 from both sides. (x + 7)(x – 3) = 0 Factor the trinomial. x + 7 = 0 or x – 3 = 0 x = – 7 or x = 3 Use the Zero Product Property. Solve each equation. The solutions are – 7 and 3. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 2 B Continued Solve the quadratic equation by factoring. Check your answer. x 2 + 4 x = 21 Check Graph the related quadratic function. The zeros of the related function should be the same as the solutions from factoring. ● Holt Mc. Dougal Algebra 1 ● The graph of y = x 2 + 4 x – 21 shows that two zeros appear to be – 7 and 3, the same as the solutions from factoring.

Solving Quadratic Equations 8 -6 by Factoring Example 2 C: Solving Quadratic Equations by Factoring Solve the quadratic equation by factoring. Check your answer. x 2 – 12 x + 36 = 0 (x – 6) = 0 x – 6 = 0 or x – 6 = 0 x=6 or x=6 Factor the trinomial. Use the Zero Product Property. Solve each equation. Both factors result in the same solution, so there is one solution, 6. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 2 C Continued Solve the quadratic equation by factoring. Check your answer. x 2 – 12 x + 36 = 0 Check Graph the related quadratic function. The graph of y = x 2 – 12 x + 36 shows that one zero appears to be 6, the same as the solution from factoring. ● Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Example 2 D: Solving Quadratic Equations by Factoring Solve the quadratic equation by factoring. Check your answer. – 2 x 2 = 20 x + 50 The equation must be written in – 2 x 2 = 20 x + 50 +2 x 2 standard form. So add 2 x 2 to 0 = 2 x 2 + 20 x + 50 both sides. 2 x 2 + 20 x + 50 = 0 Factor out the GCF 2. 2(x 2 + 10 x + 25) = 0 2(x + 5) = 0 2≠ 0 or x+5=0 x = – 5 Holt Mc. Dougal Algebra 1 Factor the trinomial. Use the Zero Product Property. Solve the equation.

Solving Quadratic Equations 8 -6 by Factoring Example 2 D Continued Solve the quadratic equation by factoring. Check your answer. – 2 x 2 = 20 x + 50 Check – 2 x 2 = 20 x + 50 – 2(– 5)2 – 50 Holt Mc. Dougal Algebra 1 20(– 5) + 50 – 100 + 50 – 50 Substitute – 5 into the original equation.

Solving Quadratic Equations 8 -6 by Factoring Helpful Hint (x – 3) is a perfect square. Since both factors are the same, you solve only one of them. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 a Solve the quadratic equation by factoring. Check your answer. x 2 – 6 x + 9 = 0 Factor the trinomial. (x – 3) = 0 x – 3 = 0 or x – 3 = 0 Use the Zero Product Property. Solve each equation. x = 3 or x = 3 Both equations result in the same solution, so there is one solution, 3. Check x 2 – 6 x + 9 = 0 Substitute 3 into the original equation. (3)2 – 6(3) + 9 0 9 – 18 + 9 0 0 0 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 b Solve the quadratic equation by factoring. Check your answer. x 2 + 4 x = 5 – 5 x 2 + 4 x – 5 = 0 (x – 1)(x + 5) = 0 x – 1 = 0 or x + 5 = 0 x=1 or x = – 5 Write the equation in standard form. Add – 5 to both sides. Factor the trinomial. Use the Zero Product Property. Solve each equation. The solutions are 1 and – 5. Holt Mc. Dougal Algebra 1

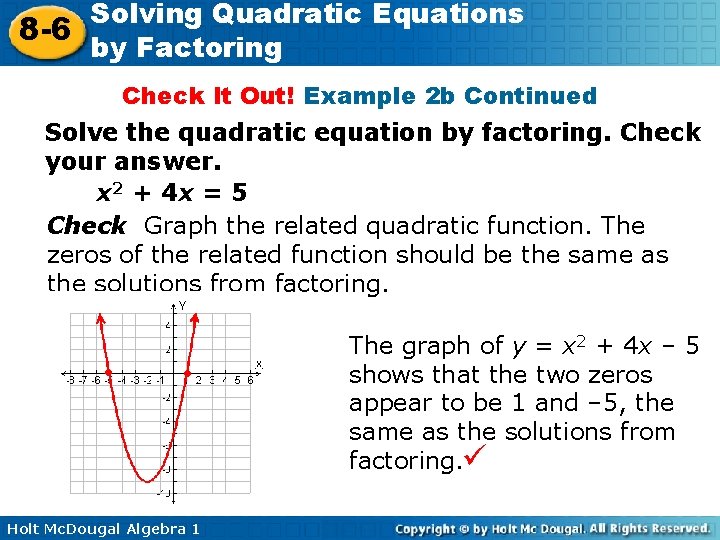
Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 b Continued Solve the quadratic equation by factoring. Check your answer. x 2 + 4 x = 5 Check Graph the related quadratic function. The zeros of the related function should be the same as the solutions from factoring. ● ● Holt Mc. Dougal Algebra 1 The graph of y = x 2 + 4 x – 5 shows that the two zeros appear to be 1 and – 5, the same as the solutions from factoring.

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 c Solve the quadratic equation by factoring. Check your answer. 30 x = – 9 x 2 – 25 – 9 x 2 – 30 x – 25 = 0 Write the equation in standard form. – 1(9 x 2 + 30 x + 25) = 0 Factor out the GCF, – 1(3 x + 5) = 0 Factor the trinomial. – 1 ≠ 0 Use the Zero Product Property. – 1 cannot equal 0. or 3 x + 5 = 0 Solve the remaining equation. Holt Mc. Dougal Algebra 1

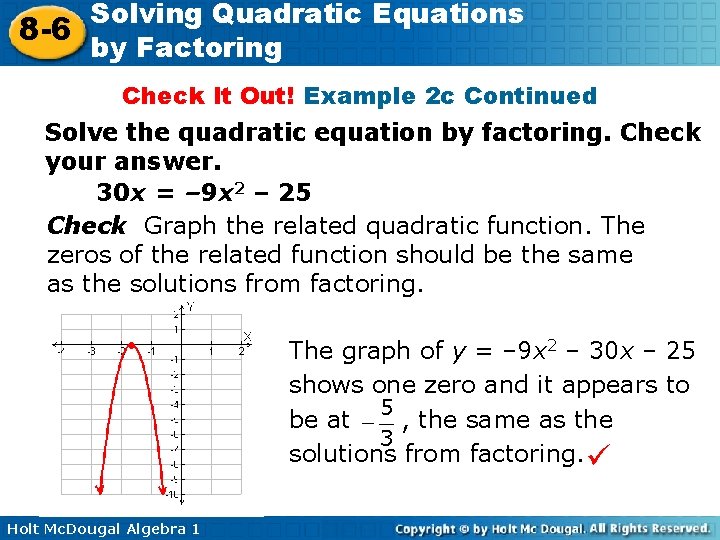
Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 c Continued Solve the quadratic equation by factoring. Check your answer. 30 x = – 9 x 2 – 25 Check Graph the related quadratic function. The zeros of the related function should be the same as the solutions from factoring. ● Holt Mc. Dougal Algebra 1 The graph of y = – 9 x 2 – 30 x – 25 shows one zero and it appears to be at , the same as the solutions from factoring.

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 d Solve the quadratic equation by factoring. Check your answer. 3 x 2 – 4 x + 1 = 0 (3 x – 1)(x – 1) = 0 3 x – 1 = 0 or x = 1 The solutions are Holt Mc. Dougal Algebra 1 Factor the trinomial. Use the Zero Product Property. Solve each equation. and x = 1.

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 2 d Continued Solve the quadratic equation by factoring. Check your answer. 3 x 2 – 4 x + 1 = 0 Check 3 x 2 – 4 x + 1 = 0 3 – 4 +1 0 Holt Mc. Dougal Algebra 1 0 0 Check 3 x 2 – 4 x + 1 = 3(1)2 – 4(1) + 1 3– 4+1 0 0 0

Solving Quadratic Equations 8 -6 by Factoring Example 3: Application The height in feet of a diver above the water can be modeled by h(t) = – 16 t 2 + 8 t + 8, where t is time in seconds after the diver jumps off a platform. Find the time it takes for the diver to reach the water. h = – 16 t 2 + 8 t + 8 0 = – 8(2 t 2 – t – 1) The diver reaches the water when h = 0. Factor out the GFC, – 8. 0 = – 8(2 t + 1)(t – 1) Factor the trinomial. 0= – 16 t 2 Holt Mc. Dougal Algebra 1 + 8 t + 8

Solving Quadratic Equations 8 -6 by Factoring Example 3 Continued Use the Zero Product – 8 ≠ 0, 2 t + 1 = 0 or t – 1= 0 Property. 2 t = – 1 or t = 1 It takes the diver 1 second to reach the water. Solve each equation. Since time cannot be negative, does not make sense in this situation. Check 0 = – 16 t 2 + 8 t + 8 0 – 16(1)2 + 8(1) + 8 Substitute 1 into the original equation. 0 – 16 + 8 0 0 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 3 What if…? The equation for the height above the water for another diver can be modeled by h = – 16 t 2 + 8 t + 24. Find the time it takes this diver to reach the water. h = – 16 t 2 + 8 t + 24 0= – 16 t 2 + 8 t + 24 The diver reaches the water when h = 0. 0 = – 8(2 t 2 – t – 3) Factor out the GFC, – 8. 0 = – 8(2 t – 3)(t + 1) Factor the trinomial. Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Check It Out! Example 3 Continued – 8 ≠ 0, 2 t – 3 = 0 or t + 1= 0 2 t = 3 or t = – 1 t = 1. 5 It takes the diver 1. 5 seconds to reach the water. Use the Zero Product Property. Solve each equation. Since time cannot be negative, – 1 does not make sense in this situation. Check 0 = – 16 t 2 + 8 t + 24 0 – 16(1. 5)2 + 8(1. 5) + 24 Substitute 1 into the 0 – 36 + 12 + 24 original equation. 0 0 Holt Mc. Dougal Algebra 1

Solving Quadratic Equations 8 -6 by Factoring Lesson Quiz: Part I Use the Zero Product Property to solve each equation. Check your answers. 1. (x – 10)(x + 5) = 0 10, – 5 2. (x + 5)(x) = 0 – 5, 0 Solve each quadratic equation by factoring. Check your answer. 3. x 2 + 16 x + 48 = 0 – 4, – 12 4. x 2 – 11 x = – 24 • Holt Mc. Dougal Algebra 1 3, 8

Solving Quadratic Equations 8 -6 by Factoring Lesson Quiz: Part II 5. 2 x 2 + 12 x – 14 = 0 1, – 7 6. x 2 + 18 x + 81 = 0 7. – 4 x 2 = 16 x + 16 – 9 – 2 8. The height of a rocket launched upward from a 160 foot cliff is modeled by the function h(t) = – 16 t 2 + 48 t + 160, where h is height in feet and t is time in seconds. Find the time it takes the rocket to reach the ground at the bottom of the cliff. 5 s Holt Mc. Dougal Algebra 1