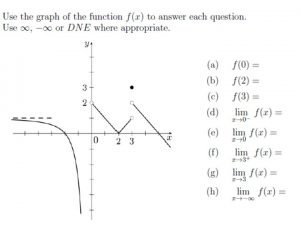
Solving Quadratics Algebraically Mrs Daniel Algebra 1 Table

Solving Quadratics Algebraically Mrs. Daniel- Algebra 1

Table of Contents 1. 2. 3. 4. 5. Introduction to Solving Quadratics Solving Quadratic Equations using Factoring Solving Quadratic Equations in Context Solving Quadratics using Square Roots Solving Quadratics using the Quadratic Formula

Solving Quadratics: Finding where the parabola intersects the x-axis. Also called finding the zeros of the function or the roots of the function because the function’s value is zero when x = p and x = q. p q

Requires a Calculator!

Solving Quadratic Equations with Factoring

Solving Equations with Factoring 1. Simplify equation into ax 2 + bx +c = 0 2. Factor equation. 3. Set each factor equal to zero and solve.

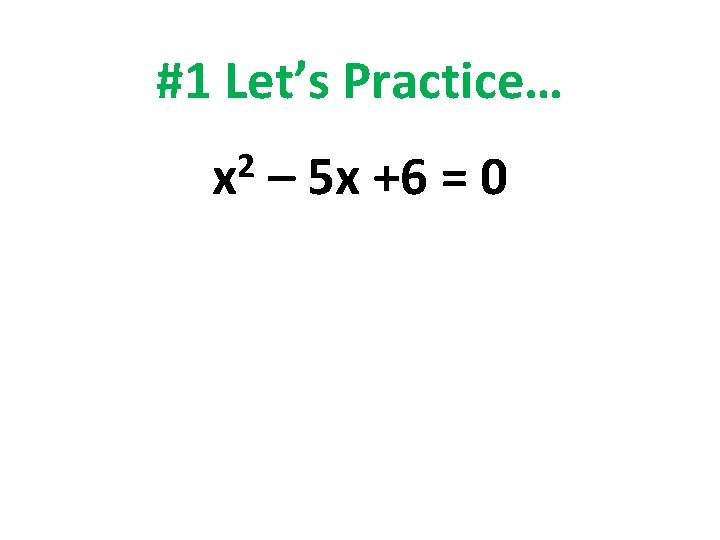
#1 Let’s Practice… 2 x – 5 x +6 = 0

2. A rectangular porch has dimension of (x + 12) and (x + 5) feet. If the area of the porch floor is 120 square feet, what are the length and the width?

3. The area of a rectangular fountain is (x 2 + 12 x + 20) square feet. A 2 -foot walkway is built around the fountain. Find the dimensions of the outside border of the walkway.

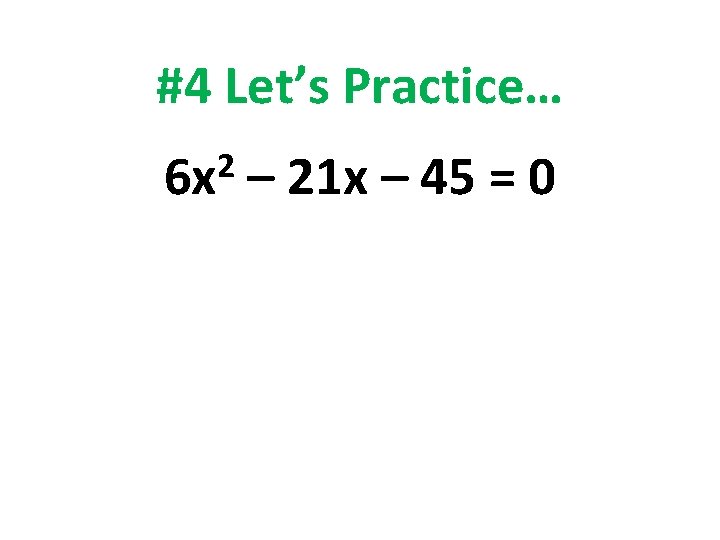
#4 Let’s Practice… 2 6 x – 21 x – 45 = 0

#5 Let’s Practice… 2 5 x + 30 x + 14 = 2 - 2 x

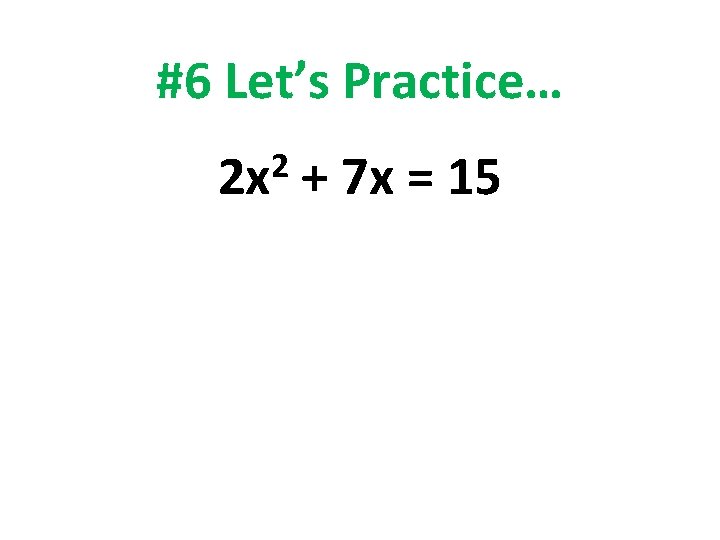
#6 Let’s Practice… 2 2 x + 7 x = 15

Solving Quadratic Equations in Context

Projectile Motion The height of a projectile at a time can be found using the formula h = -16 t 2 + vt + s. v = is the initial upwards velocity s = starting height in feet We generally solve for t and/or h.

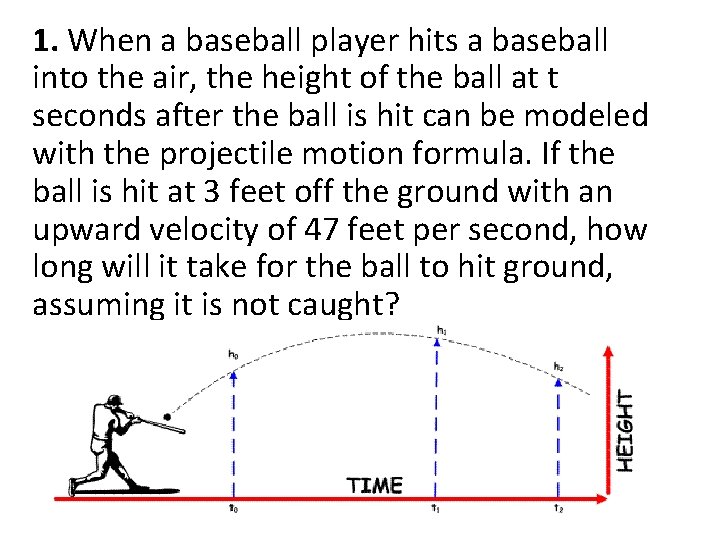
1. When a baseball player hits a baseball into the air, the height of the ball at t seconds after the ball is hit can be modeled with the projectile motion formula. If the ball is hit at 3 feet off the ground with an upward velocity of 47 feet per second, how long will it take for the ball to hit ground, assuming it is not caught?

2. A child standing on a river bank ten feet above the river throws a rock toward the river at a speed of 12 feet per second. How long does it take before the rock splashed into the river?

3. As a satellite drops from outer space onto Mars, its distance in miles from the planet is given by the formula d = -9 t 2 + 776 where t is the number of hours it has fallen. Find when the satellite will be 200 miles away from Mars.

4. A volleyball player sets the ball in the air, and the height of the ball after t seconds is given by h = -16 t 2 + 12 t + 6. A teammate wants to wait until the ball is 8 feet in the air before she spikes it. When (what time) should the teammate spike the ball? How many reasonable solutions are there to this problem?

5. An adventurous passenger jumps out of an airplane when the plane is 1000 feet above the ground. The jumper has an initial velocity of 60 feet per second downwards. How long does it take to fall from 1000 feet to 900 feet before the parachute opens?

6. A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16 t 2 + 40 ft + 1. 5. Find the maximum height attained by the ball.

Solving Quadratics using Square Roots

Square Root 1. Simplify equation. Get x 2 alone. 2. Take square root of each side. 3. Remember to consider positive and negative solutions.

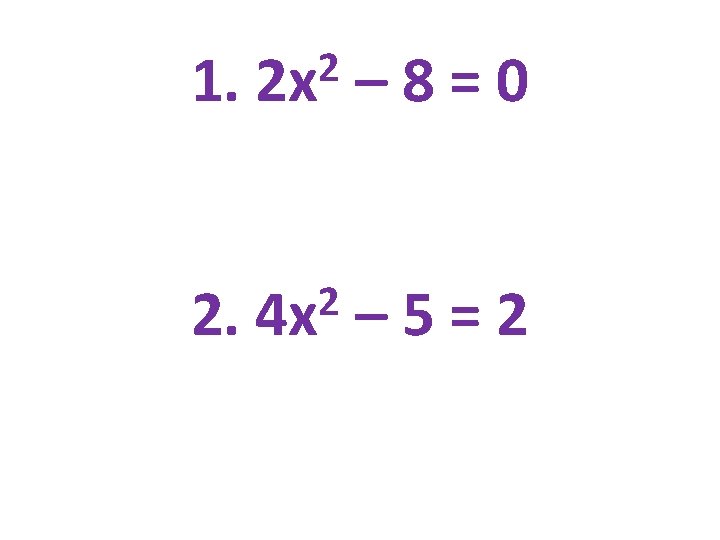
1. 2 2 x – 8=0 2. 2 4 x – 5=2

3. A contractor is building a fenced-in playground at a daycare. The playground will be rectangular with its width equal to half its length. The total area will be 5000 square feet. Determine how many feet of fencing the contractor will use.

4. (x + 2 5) = 36

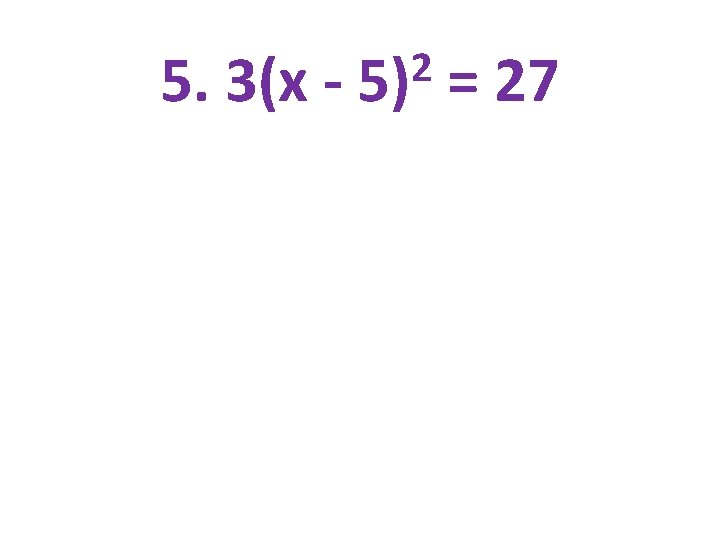
5. 3(x - 2 5) = 27

6. A person kicks a soccer ball from the ground with an initial upward velocity of 16 feet per second. What is the maximum height of the soccer ball? When will the soccer ball hit the ground?

Solving Quadratics using the Quadratic Formula

The Quadratic Formula 1. Identify a, b and c. 2. Plug in. 3. Simplify under radical. 4. Separate positive and negative solutions. 5. Solve.

Let’s Practice… 1. Solve:

Let’s Practice… 2. Solve:

Let’s Practice… Solve using the Quadratic Equation. 3. 2 x 2 + 5 x + 3 = 0

Let’s Practice… Solve using the Quadratic Equation. 4. 5 x 2 + 16 x – 84 = 0

The Discriminant You can use the discriminant to determine the number and type of solutions to the equation.

5. Find the discriminant and give the number of solutions of the equation.

Use the Discriminant to determine # of solutions; verify in context 6. A diver jumps from a platform 10 meters above the surface of the water. The diver’s height is given by the equation h = - 4. 9 t 2 + 3. 5 t + 10 where t is the time in seconds after the diver jumps. For what time t is the diver’s height 1 meter?

Use the Discriminant to determine # of solutions; verify in context 7. The height in meters of a model rocket on a particular launch can be modeled by the equation h = -4. 9 t 2 + 102 t + 100, where t is the time in seconds after its engine burns out 100 meters above the ground. When will the rocket reach a height of 600 meters?

9. The height of a ball t seconds after it’s thrown into the air from the top of a 74 ft tall building can be modeled by h(t) = – 16 t 2 + 48 t + 74, where h(t) is height in feet. The ball then lands on another building that is 10 feet off the ground. How long does it take for the ball to land on the second building?