Solving Quadratics by Completing the Square Quadratic Formula

Solving Quadratics by Completing the Square & Quadratic Formula By: Jeffrey Bivin Lake Zurich High School jeff. bivin@lz 95. org Last Updated: October 24, 2007

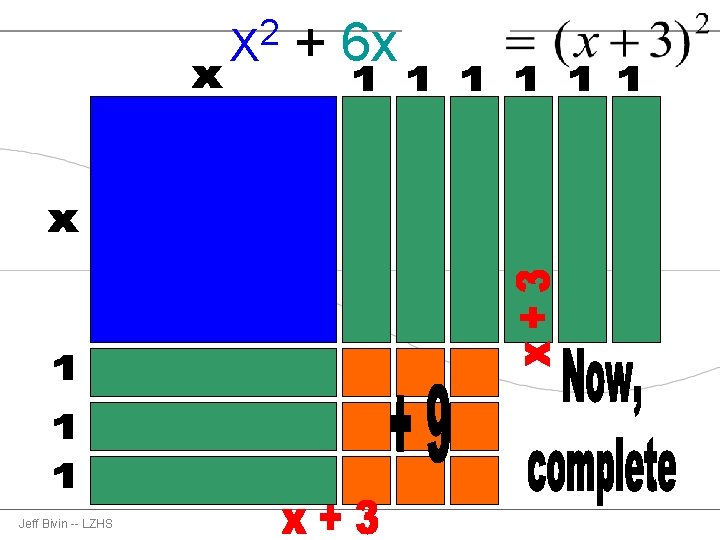
2 X Jeff Bivin -- LZHS + 6 x + 9

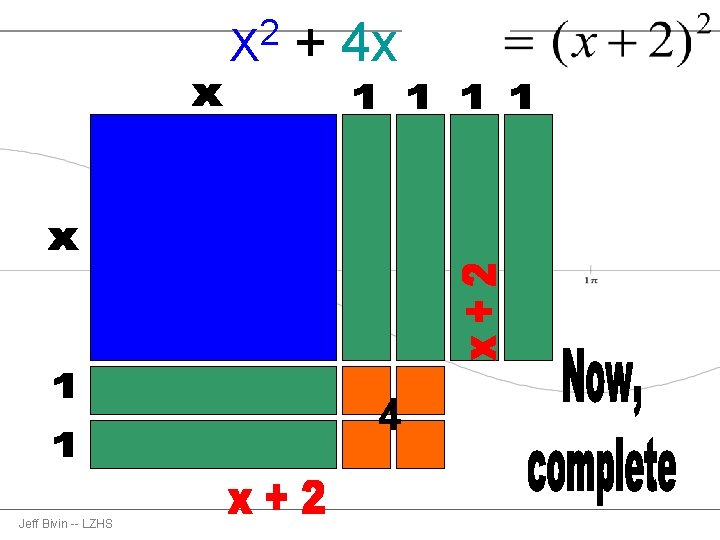
2 X + 4 x + 4 4 Jeff Bivin -- LZHS

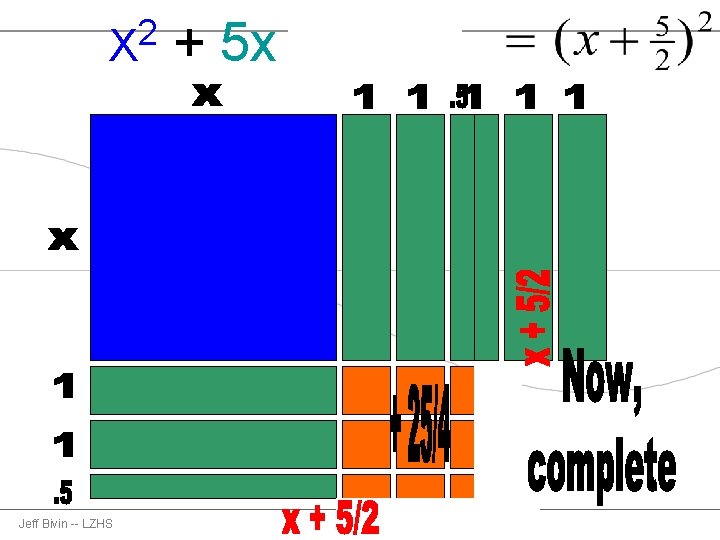
2 X Jeff Bivin -- LZHS + 5 x + 25/4

2 X Jeff Bivin -- LZHS - 6 x + 9

Solve by Completing the Square x 2 + 10 x + 8 = 0 (x 2 + 10 x (5)2 = 25 ) = -8 (x 2 + 10 x + (5)2) = -8 + 25 (x + 5)2 = 17 Jeff Bivin -- LZHS

Solve by Completing the Square 3 x 2 + 24 x + 12 = 0 3 x 2 + 8 x + 4 = 0 (x 2 + 8 x (4)2 = 16 ) = -4 (x 2 + 8 x + (4)2) = -4 + 16 (x + 4)2 = 12 Jeff Bivin -- LZHS

Solve by Completing the Square 2 x 2 + 5 x - 12 = 0 2 Jeff Bivin -- LZHS

Solve by Completing the Square 2 x 2 - 12 x - 11 = 0 2 Jeff Bivin -- LZHS

Solve by Completing the Square -5 x 2 + 12 x + 19 = 0 -5 Jeff Bivin -- LZHS

Solve by Completing the Square 5 x 2 - 30 x + 45 = 0 5 Jeff Bivin -- LZHS

Solve by Completing the Square 5 x 2 - 30 x + 75 = 0 5 Jeff Bivin -- LZHS

Convert to vertex form y = x 2 + 10 x + 8 (5)2 = 25 y - 8 = (x 2 + 10 x ) y - 8 + 25 = (x 2 + 10 x + (5)2) y + 17 = (x + 5)2 - 17 x+5=0 Axis of symmetry: Vertex: (-5, -17) Jeff Bivin -- LZHS x = -5

Convert to vertex form y = 5 x 2 - 30 x + 46 5(-3)2 = 45 y - 46 = 5(x 2 - 6 x ) y - 46 + 45 = 5(x 2 - 6 x + (-3)2) y - 1 = 5(x - 3)2 + 1 x-3=0 Axis of symmetry: Vertex: (3, 1) Jeff Bivin -- LZHS x=3

Solve by Completing the Square ax 2 + bx + c = 0 a Jeff Bivin -- LZHS

Solve using the Quadratic Formula 3 x 2 + 7 x - 4 = 0 a=3 b=7 c = -4 Jeff Bivin -- LZHS

Solve using the Quadratic Formula 6 x 2 + 9 x + 2 = 0 a=6 b=9 c=2 Jeff Bivin -- LZHS

Solve using the Quadratic Formula 5 x 2 - 8 x + 1 = 0 a=5 b = -8 c=1 Jeff Bivin -- LZHS

Solve using the Quadratic Formula 6 x 2 - 17 x - 14 = 0 a=6 b = -17 c = -14 Jeff Bivin -- LZHS

Solve using the Quadratic Formula x 2 + 6 x + 9 = 0 a=1 b=6 c=9 Jeff Bivin -- LZHS

Solve using the Quadratic Formula 3 x 2 + 7 x + 5 = 0 a=3 b=7 c=5 Jeff Bivin -- LZHS

Why do some quadratic equations have 2 real solutions some have 1 real solution and some have two imaginary solutions?

Now Consider ax 2 + bx + c = 0 89 -011 If discriminant > 0, then 2 real solutions If discriminant = 0, then 1 real solution If discriminant < 0, then 2 imaginary solutions Jeff Bivin -- LZHS

Jeff Bivin -- LZHS