Solving one step equations with algebra tiles Standard

Solving one step equations with algebra tiles Standard 6. 10 A

Algebra Tiles: l We have 2 types of tiles we will be working with this year: x x 1 1 So, we name the tiles by their areas: x’s and ones (unit tiles).

How can we show zero with the tiles? l l l A zero is a positive and negative tile of the same type. We show a negative with the tiles by it’s color. The RED side is negative. If we are drawing a picture, the NON-shaded tile is Negative. Ex: =0 =0

Why do we need to solve equations? We need to find the value of the variable that makes the equation true. How to solve equations: a) Make zeros to get rid of unit tiles…put the same number of tiles on BOTH sides of the equal sign. b) Divide (partition) up unit tiles on one side so EACH “x” tile receives the same number of unit tiles. c) If “x” tiles are negative, flip all tiles to their opposite sign. d) If an “x” tile is being divided into parts, EACH part has the SAME number of unit tiles in it. Count how many unit tiles are in the WHOLE “x” tile. Let’s look at each step separately!

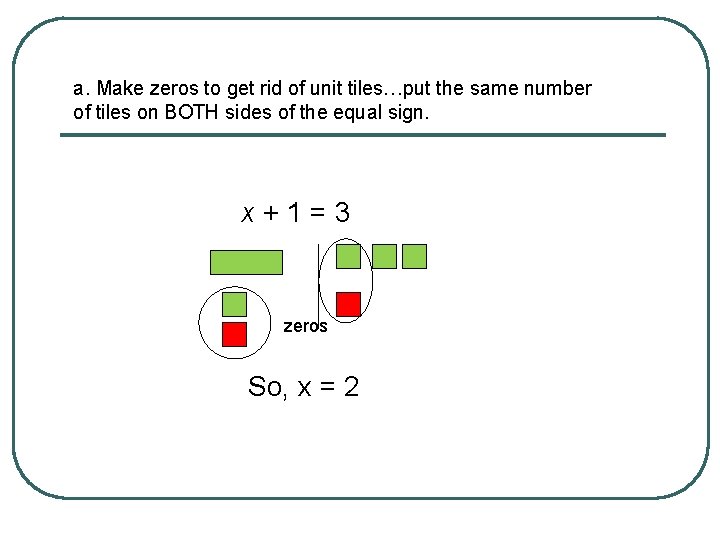
a. Make zeros to get rid of unit tiles…put the same number of tiles on BOTH sides of the equal sign. x+1=3 zeros So, x = 2

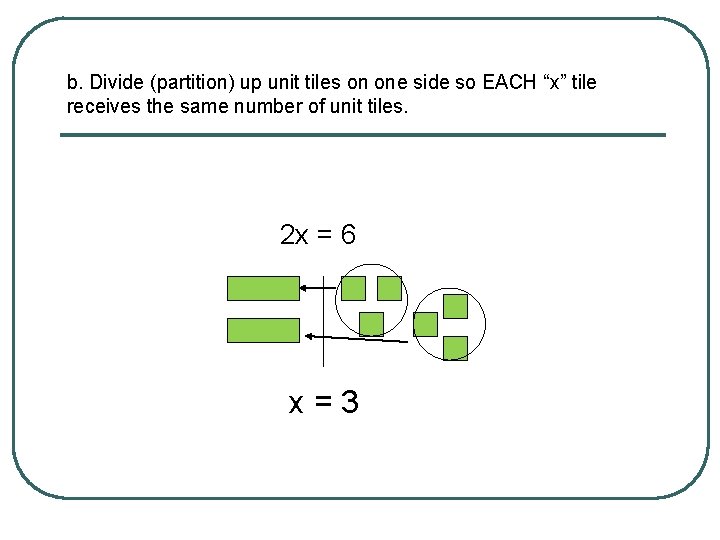
b. Divide (partition) up unit tiles on one side so EACH “x” tile receives the same number of unit tiles. 2 x = 6 x=3

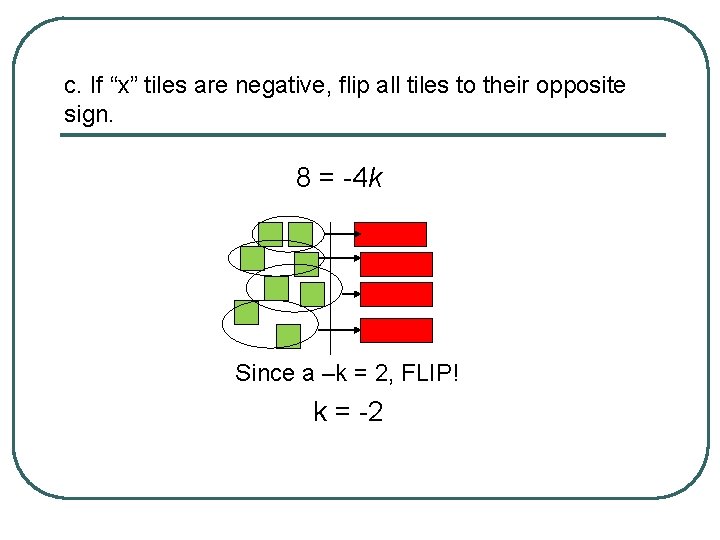
c. If “x” tiles are negative, flip all tiles to their opposite sign. 8 = -4 k Since a –k = 2, FLIP! k = -2

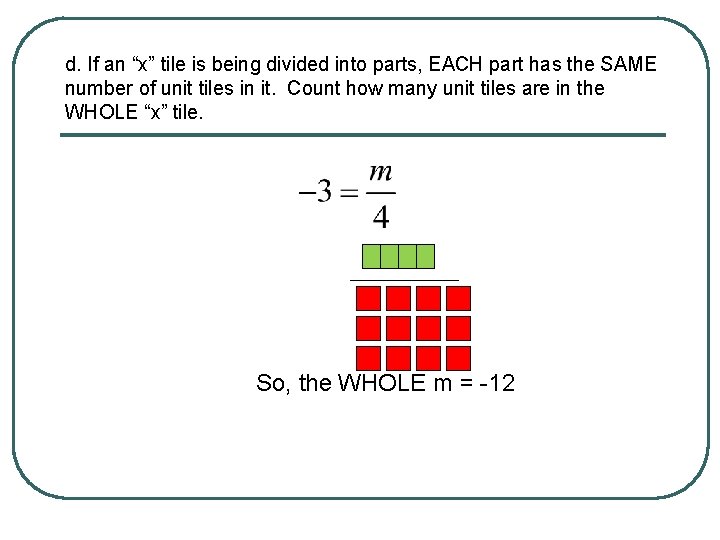
d. If an “x” tile is being divided into parts, EACH part has the SAME number of unit tiles in it. Count how many unit tiles are in the WHOLE “x” tile. So, the WHOLE m = -12