12 VECTORS AND THE GEOMETRY OF SPACE VECTORS














































































- Slides: 108

12 VECTORS AND THE GEOMETRY OF SPACE

VECTORS AND THE GEOMETRY OF SPACE 12. 2 Vectors In this section, we will learn about: Vectors and their applications.

VECTOR The term vector is used by scientists to indicate a quantity (such as displacement or velocity or force) that has both magnitude and direction.

REPRESENTING A VECTOR A vector is often represented by an arrow or a directed line segment. § The length of the arrow represents the magnitude of the vector. § The arrow points in the direction of the vector.

DENOTING A VECTOR We denote a vector by either: § Printing a letter in boldface (v) § Putting an arrow above the letter ( )

VECTORS For instance, suppose a particle moves along a line segment from point A to point B.

VECTORS The corresponding displacement vector v has initial point A (the tail) and terminal point B (the tip). § We indicate this by writing v =.

VECTORS Notice that the vector u = has the same length and the same direction as v even though it is in a different position. § We say u and v are equivalent (or equal) and write u = v.

ZERO VECTOR The zero vector, denoted by 0, has length 0. § It is the only vector with no specific direction.

COMBINING VECTORS Suppose a particle moves from A to B. So, its displacement vector is .

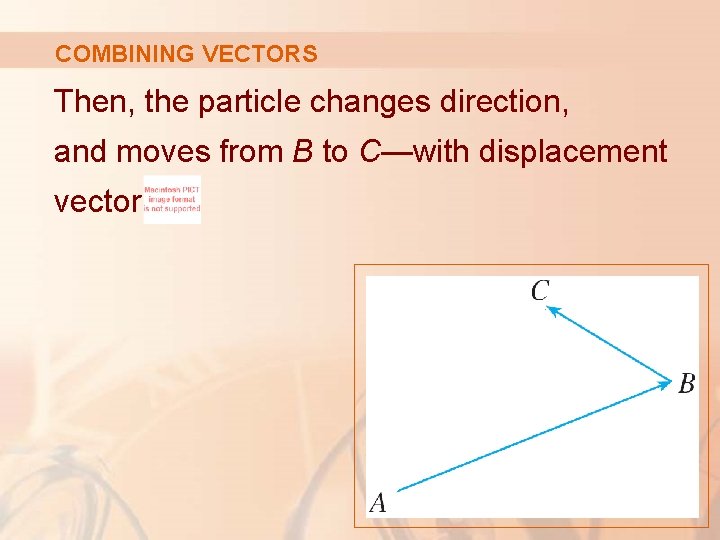
COMBINING VECTORS Then, the particle changes direction, and moves from B to C—with displacement vector .

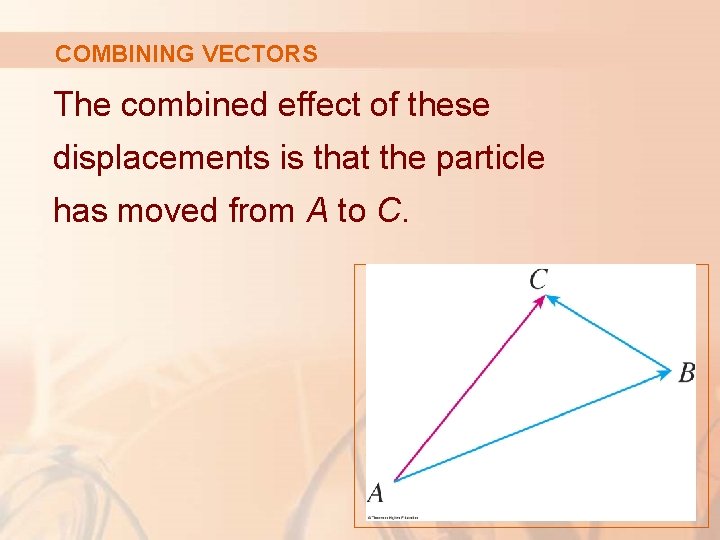
COMBINING VECTORS The combined effect of these displacements is that the particle has moved from A to C.

COMBINING VECTORS The resulting displacement vector is called the sum of We write: and .

ADDING VECTORS In general, if we start with vectors u and v, we first move v so that its tail coincides with the tip of u and define the sum of u and v as follows.

VECTOR ADDITION—DEFINITION If u and v are vectors positioned so the initial point of v is at the terminal point of u, then the sum u + v is the vector from the initial point of u to the terminal point of v.

VECTOR ADDITION The definition of vector addition is illustrated here.

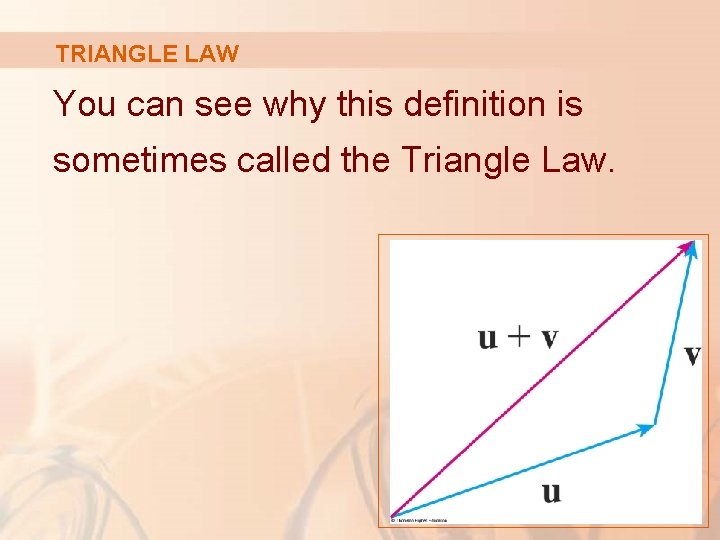
TRIANGLE LAW You can see why this definition is sometimes called the Triangle Law.

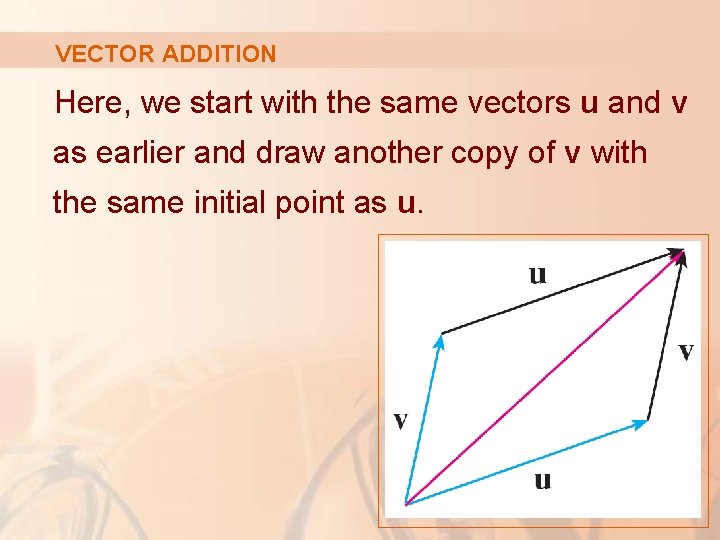
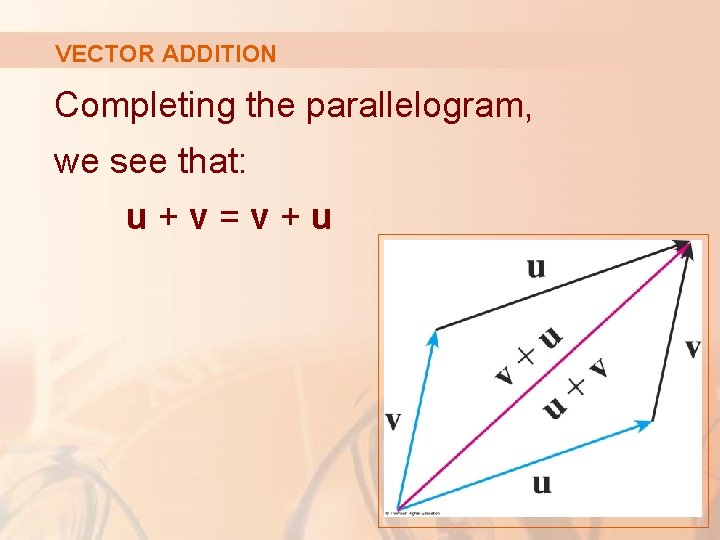
VECTOR ADDITION Here, we start with the same vectors u and v as earlier and draw another copy of v with the same initial point as u.

VECTOR ADDITION Completing the parallelogram, we see that: u+v=v+u

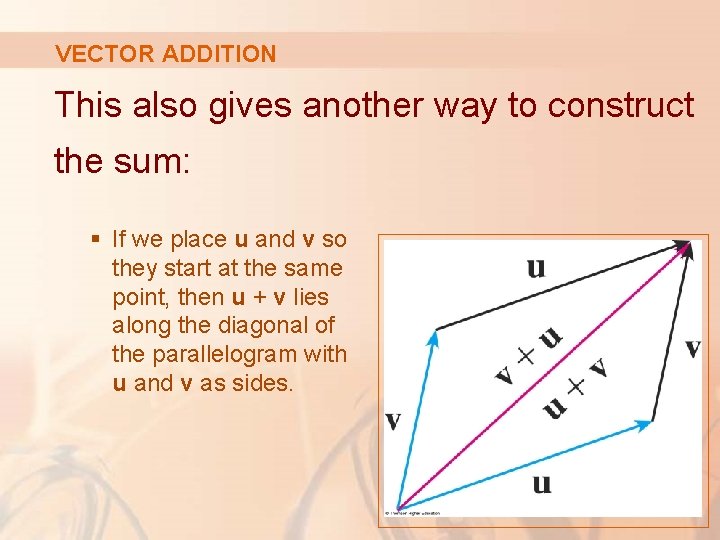
VECTOR ADDITION This also gives another way to construct the sum: § If we place u and v so they start at the same point, then u + v lies along the diagonal of the parallelogram with u and v as sides.

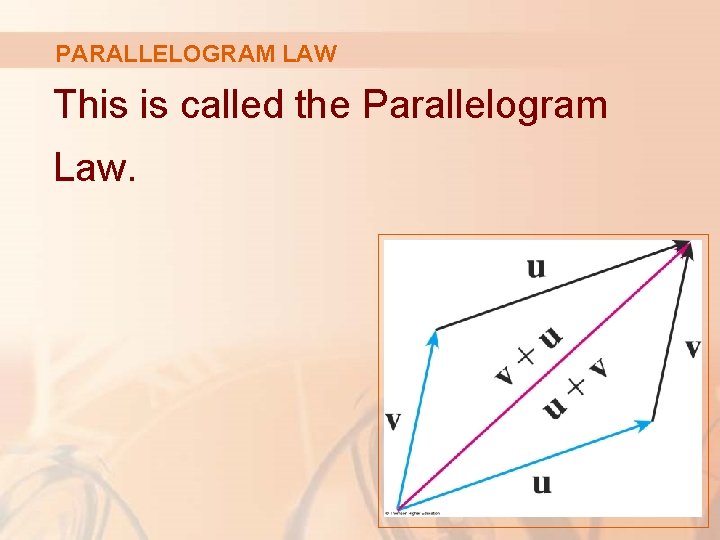
PARALLELOGRAM LAW This is called the Parallelogram Law.

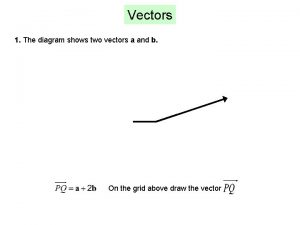
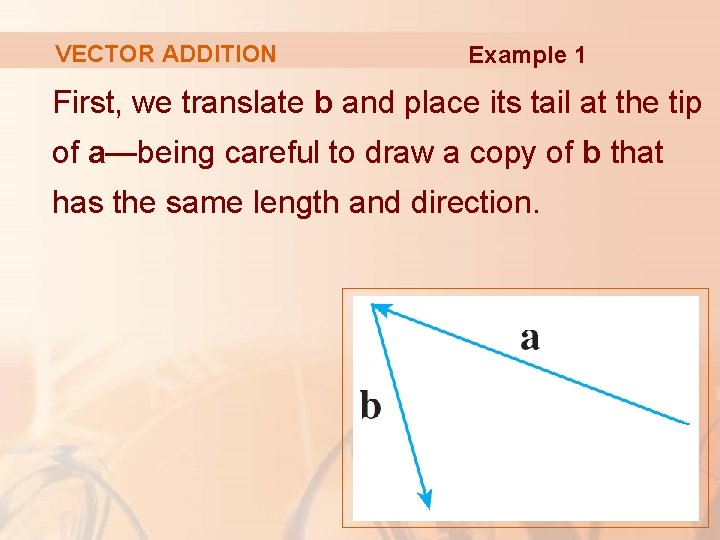
VECTOR ADDITION Example 1 Draw the sum of the vectors a and b shown here.

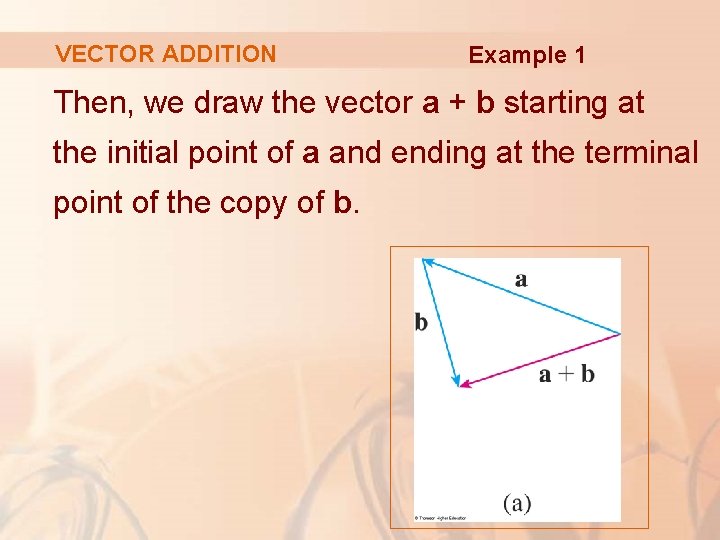
VECTOR ADDITION Example 1 First, we translate b and place its tail at the tip of a—being careful to draw a copy of b that has the same length and direction.

VECTOR ADDITION Example 1 Then, we draw the vector a + b starting at the initial point of a and ending at the terminal point of the copy of b.

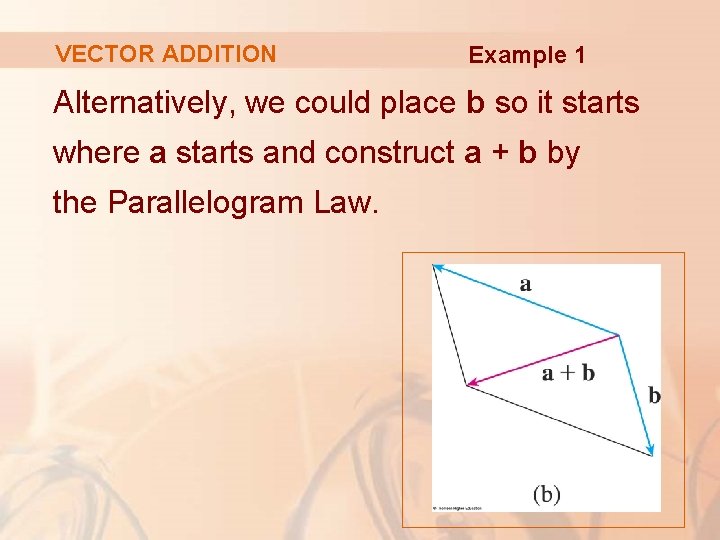
VECTOR ADDITION Example 1 Alternatively, we could place b so it starts where a starts and construct a + b by the Parallelogram Law.

MULTIPLYING VECTORS It is possible to multiply a vector by a real number c.

SCALAR In this context, we call the real number c a scalar—to distinguish it from a vector.

MULTIPLYING SCALARS For instance, we want 2 v to be the same vector as v + v, which has the same direction as v but is twice as long. In general, we multiply a vector by a scalar as follows.

SCALAR MULTIPLICATION—DEFINITION If c is a scalar and v is a vector, the scalar multiple cv is: The vector whose length is |c| times the length of v and whose direction is the same as v if c > 0 and is opposite to v if c < 0. § If c = 0 or v = 0, then cv = 0.

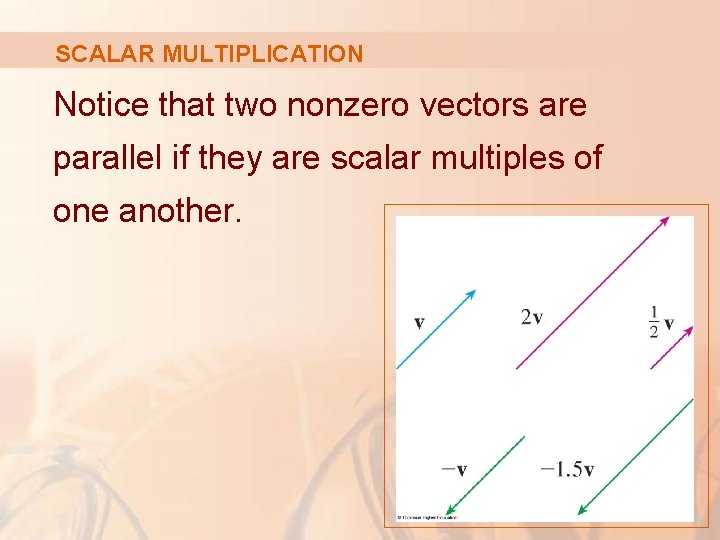
SCALAR MULTIPLICATION The definition is illustrated here. § We see that real numbers work like scaling factors here. § That’s why we call them scalars.

SCALAR MULTIPLICATION Notice that two nonzero vectors are parallel if they are scalar multiples of one another.

SCALAR MULTIPLICATION In particular, the vector –v = (– 1)v has the same length as v but points in the opposite direction. § We call it the negative of v.

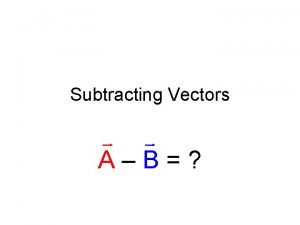
SUBTRACTING VECTORS By the difference u – v of two vectors, we mean: u – v = u + (–v)

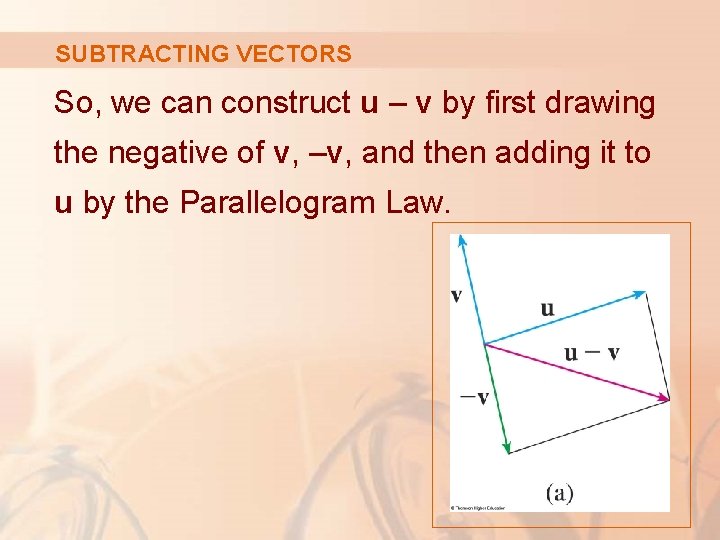
SUBTRACTING VECTORS So, we can construct u – v by first drawing the negative of v, –v, and then adding it to u by the Parallelogram Law.

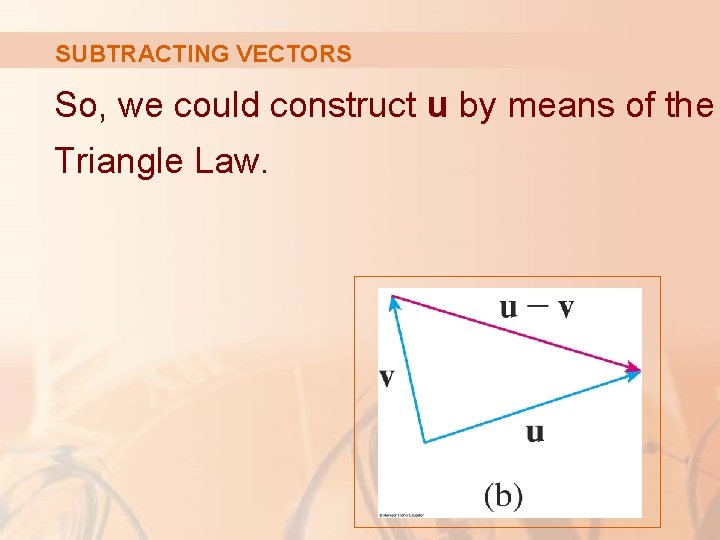
SUBTRACTING VECTORS Alternatively, since v + (u – v) = u, the vector u – v, when added to v, gives u.

SUBTRACTING VECTORS So, we could construct u by means of the Triangle Law.

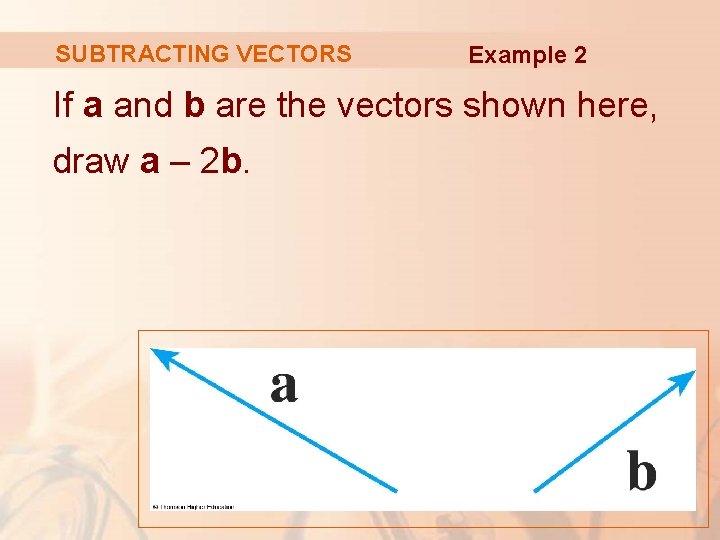
SUBTRACTING VECTORS Example 2 If a and b are the vectors shown here, draw a – 2 b.

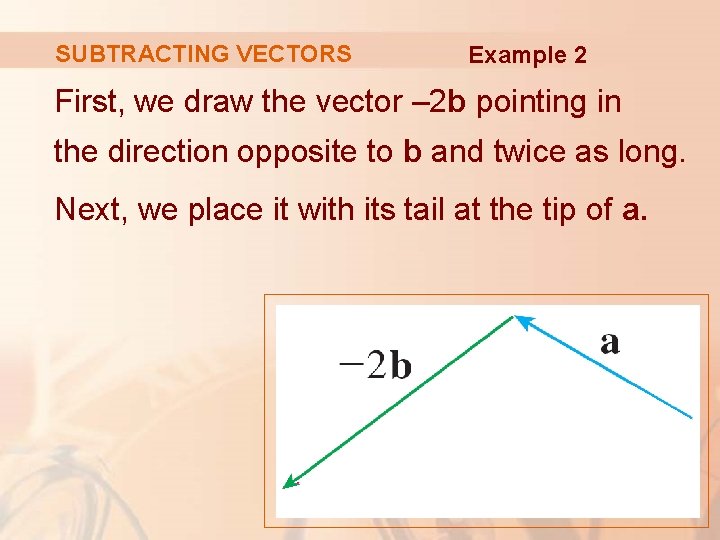
SUBTRACTING VECTORS Example 2 First, we draw the vector – 2 b pointing in the direction opposite to b and twice as long. Next, we place it with its tail at the tip of a.

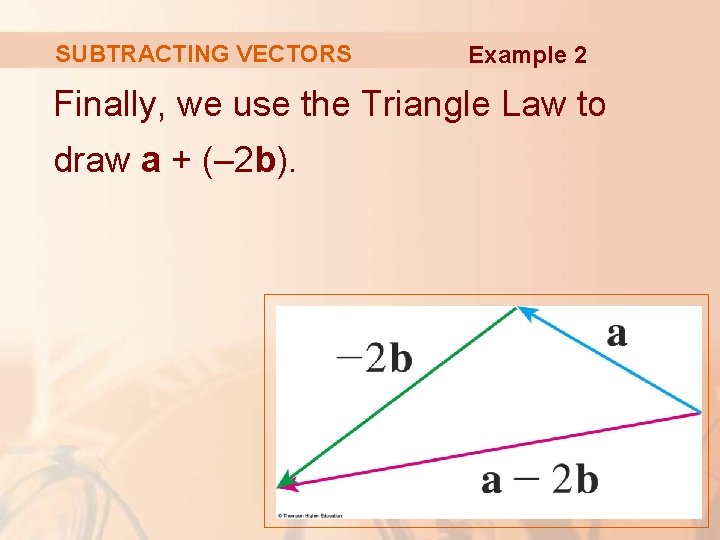
SUBTRACTING VECTORS Example 2 Finally, we use the Triangle Law to draw a + (– 2 b).

COMPONENTS For some purposes, it’s best to introduce a coordinate system and treat vectors algebraically.

COMPONENTS Let’s place the initial point of a vector a at the origin of a rectangular coordinate system.

COMPONENTS Then, the terminal point of a has coordinates of the form (a 1, a 2) or (a 1, a 2, a 3). § This depends on whether our coordinate system is two- or three-dimensional.

COMPONENTS These coordinates are called the components of a and we write: a = ‹a 1, a 2› or a = ‹a 1, a 2, a 3›

COMPONENTS We use the notation ‹a 1, a 2› for the ordered pair that refers to a vector so as not to confuse it with the ordered pair (a 1, a 2) that refers to a point in the plane.

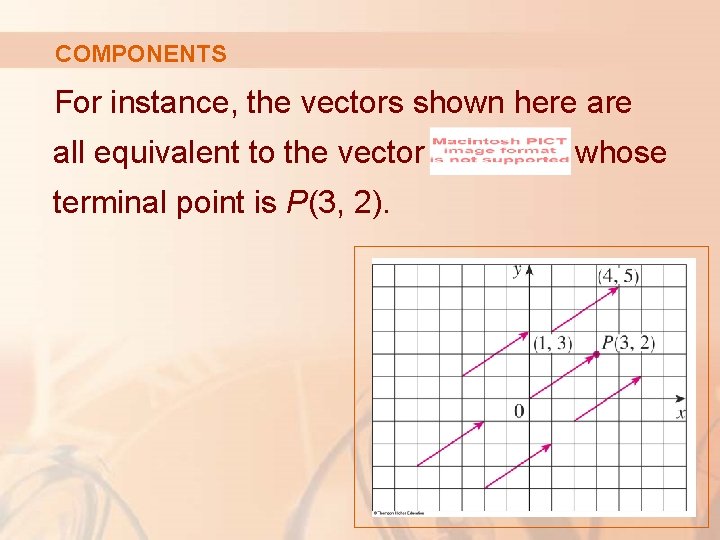
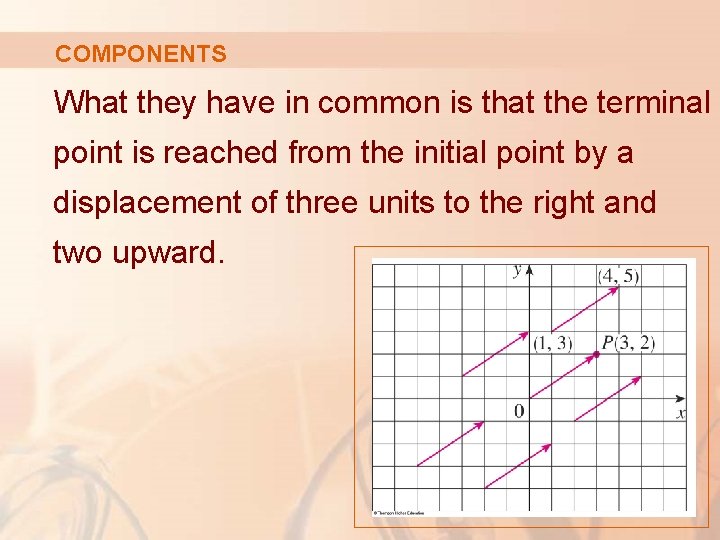
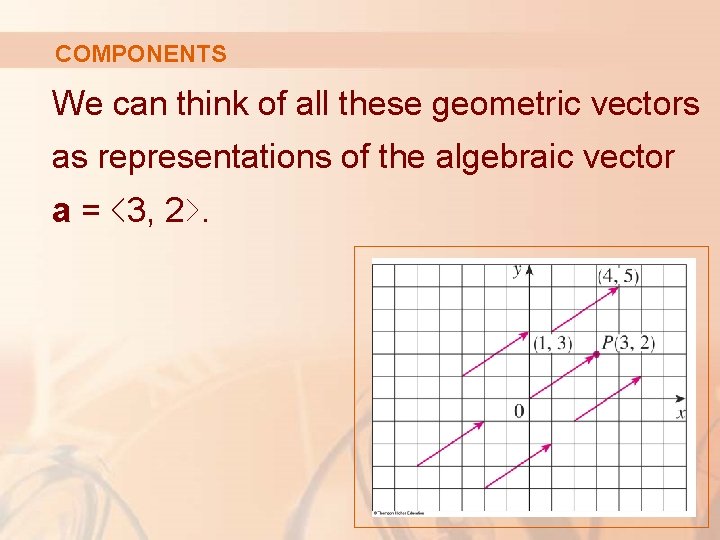
COMPONENTS For instance, the vectors shown here all equivalent to the vector terminal point is P(3, 2). whose

COMPONENTS What they have in common is that the terminal point is reached from the initial point by a displacement of three units to the right and two upward.

COMPONENTS We can think of all these geometric vectors as representations of the algebraic vector a = ‹ 3, 2›.

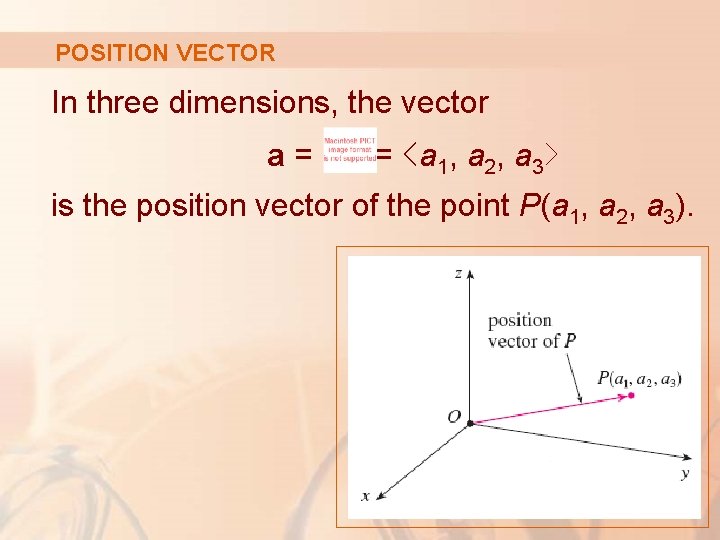
POSITION VECTOR The particular representation from the origin to the point P(3, 2) is called the position vector of the point P.

POSITION VECTOR In three dimensions, the vector a= = ‹a 1, a 2, a 3› is the position vector of the point P(a 1, a 2, a 3).

COMPONENTS Let’s consider any other representation of a, where the initial point is A(x 1, y 1, z 1) and the terminal point is B(x 2, y 2, z 2).

COMPONENTS Then, we must have: x 1 + a 1 = x 2, y 1 + a 2 = y 2, z 1 + a 3 = z 2 a 2 = y 2 – y 1, a 3 = z 2 – z 1 Thus, a 1 = x 2 – x 1, § Thus, we have the following result.

COMPONENTS Equation 1 Given the points A(x 1, y 1, z 1) and B(x 2, y 2, z 2), the vector a with representation is: a = ‹x 2 – x 1, y 2 – y 1, z 2 – z 1›

COMPONENTS Example 3 Find the vector represented by the directed line segment with initial point A(2, – 3, 4) and terminal point B(– 2, 1, 1). § By Equation 1, the vector corresponding to is: a = ‹– 2 – 2, 1 – (– 3), 1 – 4› = ‹– 4, 4, – 3›

LENGTH OF VECTOR The magnitude or length of the vector v is the length of any of its representations. § It is denoted by the symbol |v| or║v║.

LENGTH OF VECTOR By using the distance formula to compute the length of a segment the following formulas. , we obtain

LENGTH OF 2 -D VECTOR The length of the two-dimensional (2 -D) vector a = ‹a 1, a 2› is:

LENGTH OF 3 -D VECTOR The length of the three-dimensional (3 -D) vector a = ‹a 1, a 2, a 3› is:

ALGEBRAIC VECTORS How do we add vectors algebraically?

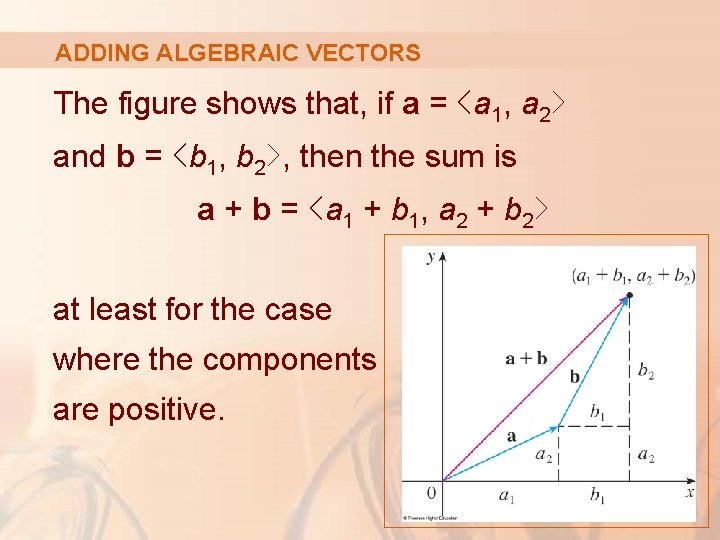
ADDING ALGEBRAIC VECTORS The figure shows that, if a = ‹a 1, a 2› and b = ‹b 1, b 2›, then the sum is a + b = ‹a 1 + b 1, a 2 + b 2› at least for the case where the components are positive.

ADDING ALGEBRAIC VECTORS In other words, to add algebraic vectors, we add their components.

SUBTRACTING ALGEBRAIC VECTORS Similarly, to subtract vectors, we subtract components.

ALGEBRAIC VECTORS From the similar triangles in the figure, we see that the components of ca are ca 1 and ca 2.

MULTIPLYING ALGEBRAIC VECTORS So, to multiply a vector by a scalar, we multiply each component by that scalar.

2 -D ALGEBRAIC VECTORS If a = ‹a 1, a 2› and b = ‹b 1, b 2›, then a + b = ‹a 1 + b 1, a 2 + b 2› a – b = ‹a 1 – b 1 , a 2 – b 2› ca = ‹ca 1, ca 2›

3 -D ALGEBRAIC VECTORS Similarly, for 3 -D vectors,

ALGEBRAIC VECTORS Example 4 If a = ‹ 4, 0, 3› and b = ‹– 2, 1, 5›, find: |a| and the vectors a + b, a – b, 3 b, 2 a + 5 b

ALGEBRAIC VECTORS |a| Example 4

ALGEBRAIC VECTORS Example 4

ALGEBRAIC VECTORS Example 4

ALGEBRAIC VECTORS Example 4

ALGEBRAIC VECTORS Example 4

COMPONENTS We denote: § V 2 as the set of all 2 -D vectors § V 3 as the set of all 3 -D vectors

COMPONENTS More generally, we will later need to consider the set Vn of all n-dimensional vectors. § An n-dimensional vector is an ordered n-tuple a = ‹a 1, a 2, …, an› where a 1, a 2, …, an are real numbers that are called the components of a.

COMPONENTS Addition and scalar multiplication are defined in terms of components just as for the cases n = 2 and n = 3.

PROPERTIES OF VECTORS If a, b, and c are vectors in Vn and c and d are scalars, then

PROPERTIES OF VECTORS These eight properties of vectors can be readily verified either geometrically or algebraically.

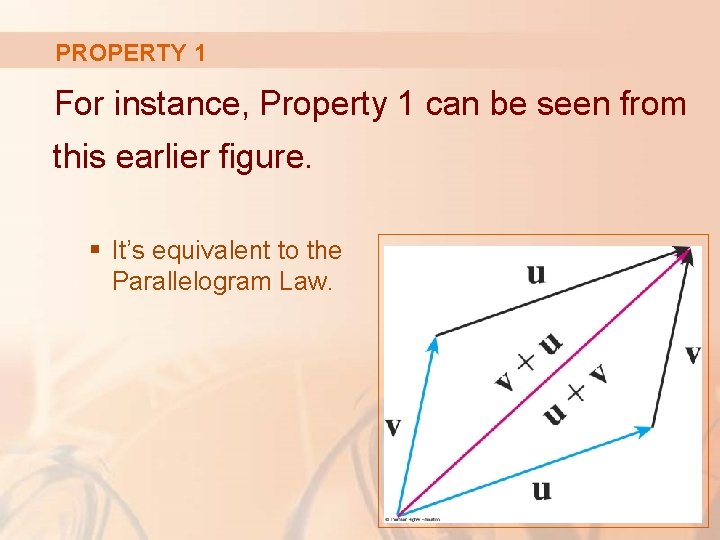
PROPERTY 1 For instance, Property 1 can be seen from this earlier figure. § It’s equivalent to the Parallelogram Law.

PROPERTY 1 It can also be seen as follows for the case n = 2: a + b = ‹a 1, a 2› + ‹b 1, b 2› = ‹a 1 + b 1, a 2 + b 2› = ‹b 1 + a 1, b 2 + a 2› = ‹b 1, b 2› + ‹a 1, a 2› =b+a

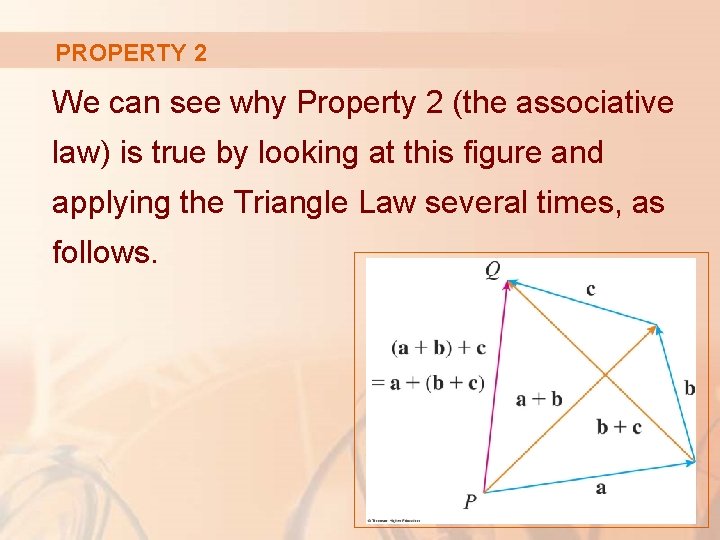
PROPERTY 2 We can see why Property 2 (the associative law) is true by looking at this figure and applying the Triangle Law several times, as follows.

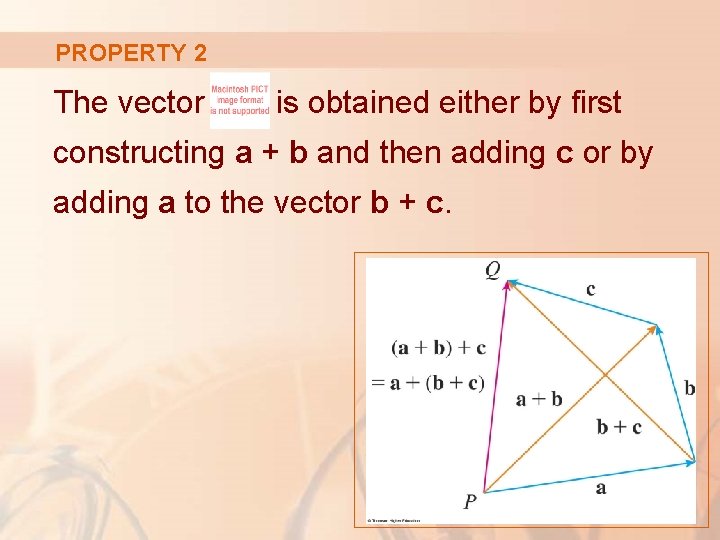
PROPERTY 2 The vector is obtained either by first constructing a + b and then adding c or by adding a to the vector b + c.

VECTORS IN V 3 Three vectors in V 3 play a special role.

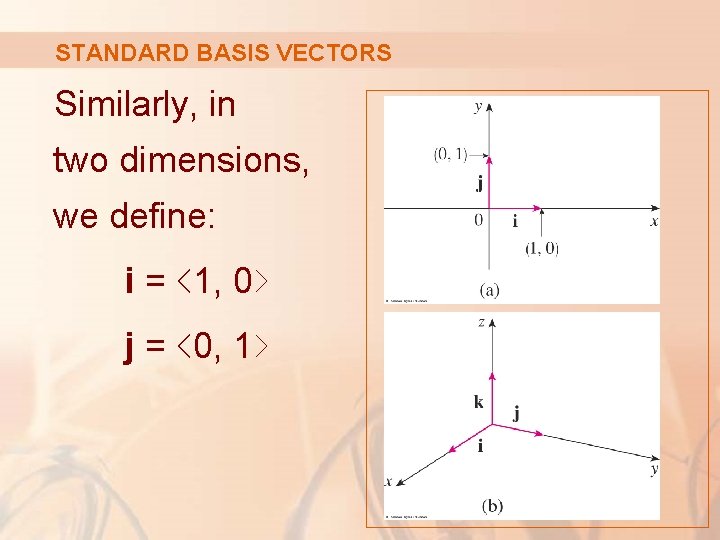
VECTORS IN V 3 Let i = ‹ 1, 0, 0› j = ‹ 0, 1, 0› k = ‹ 0, 0, 1›

STANDARD BASIS VECTORS These vectors i, j, and k are called the standard basis vectors. § They have length 1 and point in the directions of the positive x-, y-, and z-axes.

STANDARD BASIS VECTORS Similarly, in two dimensions, we define: i = ‹ 1, 0› j = ‹ 0, 1›

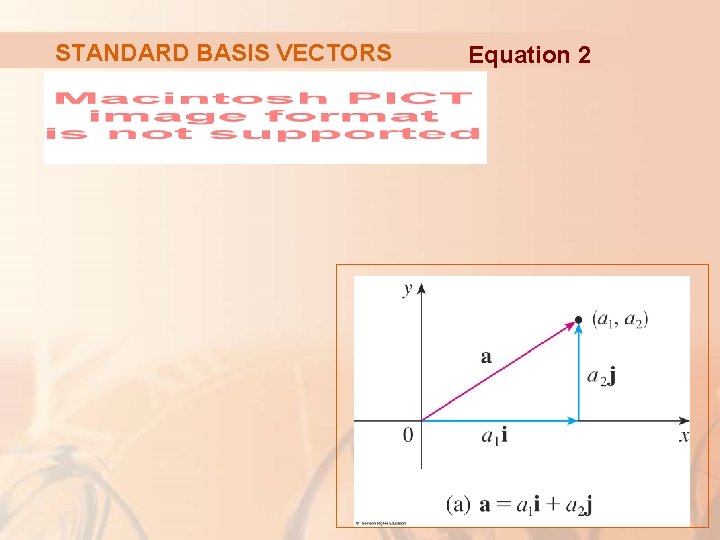
STANDARD BASIS VECTORS If a = ‹a 1, a 2, a 3›, then we can write:

STANDARD BASIS VECTORS Equation 2

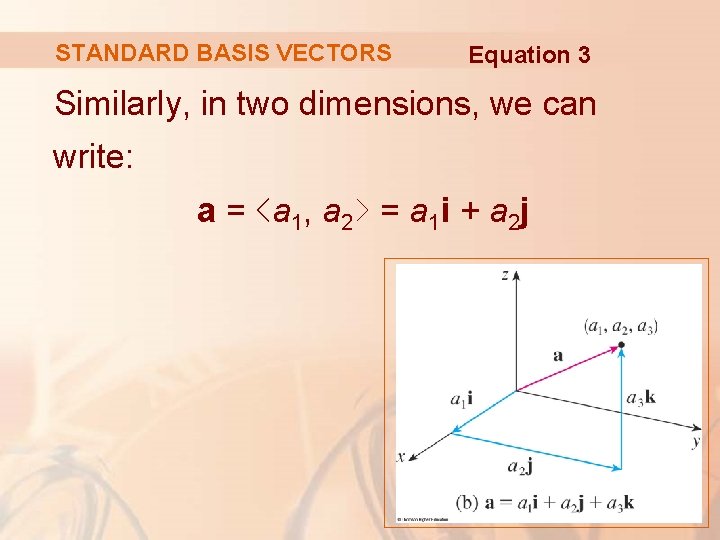
STANDARD BASIS VECTORS Thus, any vector in V 3 can be expressed in terms of i, j, and k.

STANDARD BASIS VECTORS For instance, ‹ 1, – 2, 6› = i – 2 j + 6 k

STANDARD BASIS VECTORS Equation 3 Similarly, in two dimensions, we can write: a = ‹a 1, a 2› = a 1 i + a 2 j

COMPONENTS Compare the geometric interpretation of Equations 2 and 3 with the earlier figures.

COMPONENTS Example 5 If a = i + 2 j – 3 k and b = 4 i + 7 k, express the vector 2 a + 3 b in terms of i, j, and k.

COMPONENTS Example 5 Using Properties 1, 2, 5, 6, and 7 of vectors, we have: 2 a + 3 b = 2(i + 2 j – 3 k) + 3(4 i + 7 k) = 2 i + 4 j – 6 k + 12 i + 21 k = 14 i + 4 j + 15 k

UNIT VECTOR A unit vector is a vector whose length is 1. § For instance, i, j, and k are all unit vectors.

UNIT VECTORS Equation 4 In general, if a ≠ 0, then the unit vector that has the same direction as a is:

UNIT VECTORS In order to verify this, we let c = 1/|a|. § Then, u = ca and c is a positive scalar; so, u has the same direction as a. § Also,

UNIT VECTORS Example 6 Find the unit vector in the direction of the vector 2 i – j – 2 k.

UNIT VECTORS Example 6 The given vector has length § So, by Equation 4, the unit vector with the same direction is:

APPLICATIONS Vectors are useful in many aspects of physics and engineering. § In Chapter 13, we will see how they describe the velocity and acceleration of objects moving in space. § Here, we look at forces.

FORCE A force is represented by a vector because it has both a magnitude (measured in pounds or newtons) and a direction. § If several forces are acting on an object, the resultant force experienced by the object is the vector sum of these forces.

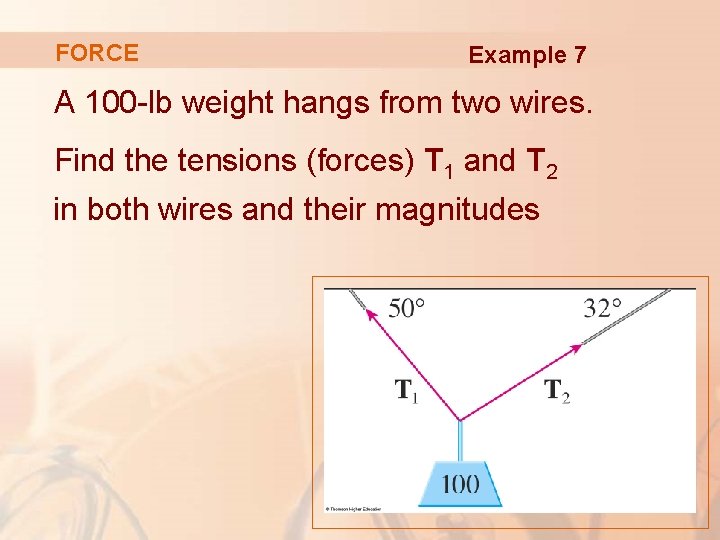
FORCE Example 7 A 100 -lb weight hangs from two wires. Find the tensions (forces) T 1 and T 2 in both wires and their magnitudes

FORCE Example 7 First, we express T 1 and T 2 in terms of their horizontal and vertical components.

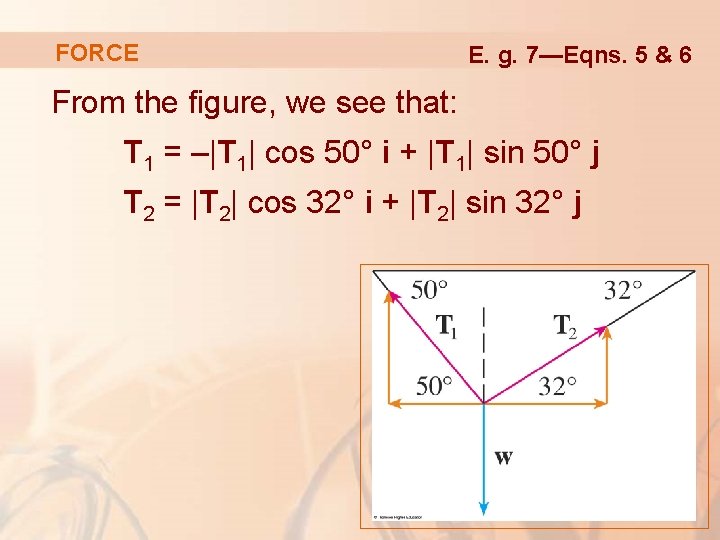
FORCE E. g. 7—Eqns. 5 & 6 From the figure, we see that: T 1 = –|T 1| cos 50° i + |T 1| sin 50° j T 2 = |T 2| cos 32° i + |T 2| sin 32° j

FORCE Example 7 The resultant T 1 + T 2 of the tensions counterbalances the weight w. So, we must have: T 1 + T 2 = –w = 100 j

FORCE Example 7 Thus, (–|T 1| cos 50° + |T 2| cos 32°) i + (|T 1| sin 50° + |T 2| sin 32°) j = 100 j

FORCE Example 7 Equating components, we get: –|T 1| cos 50° + |T 2| cos 32° = 0 |T 1| sin 50° + |T 2| sin 32° = 100

FORCE Example 7 Solving the first of these equations for |T 2| and substituting into the second, we get:

FORCE Example 7 So, the magnitudes of the tensions are:

FORCE Example 7 Substituting these values in Equations 5 and 6, we obtain the tension vectors T 1 ≈ – 55. 05 i + 65. 60 j T 2 ≈ 55. 05 i + 34. 40 j
 Vectors and the geometry of space
Vectors and the geometry of space Dot product
Dot product Chapter 12 vectors and the geometry of space
Chapter 12 vectors and the geometry of space Dot product
Dot product Vectors and the geometry of space
Vectors and the geometry of space Dot product
Dot product Lewis structure of pf3
Lewis structure of pf3 Electron domain geometry vs molecular geometry
Electron domain geometry vs molecular geometry Electron geometry vs molecular geometry
Electron geometry vs molecular geometry Cartesian space trajectory planning
Cartesian space trajectory planning Space junk the space age began
Space junk the space age began Camera space to world space
Camera space to world space Cartesian space vs joint space
Cartesian space vs joint space World space to screen space
World space to screen space Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Chụp phim tư thế worms-breton
Chụp phim tư thế worms-breton Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia Kể tên các môn thể thao
Kể tên các môn thể thao Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng xinh xinh thế chỉ nói điều hay thôi
Cái miệng xinh xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V. c c
V. c c Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Fecboak
Fecboak Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Số nguyên là gì
Số nguyên là gì Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Sơ đồ cơ thể người
Sơ đồ cơ thể người Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Big ed mona multimodal text
Big ed mona multimodal text Unit vector
Unit vector A storm system moves 5000 km due east
A storm system moves 5000 km due east Tan-1(ry/rx)
Tan-1(ry/rx) Vector direction
Vector direction A vector has both direction and:
A vector has both direction and: The diagram shows a quadrilateral pqrs
The diagram shows a quadrilateral pqrs Two dimensional motion examples
Two dimensional motion examples Scalar quantity characteristics
Scalar quantity characteristics Entropy is scalar or vector
Entropy is scalar or vector General vector spaces
General vector spaces Linearly dependent and independent vectors
Linearly dependent and independent vectors Linear independence of vectors
Linear independence of vectors Lesson plan on vectors and scalars
Lesson plan on vectors and scalars Vectors have magnitude and direction
Vectors have magnitude and direction Trigonometry and vectors
Trigonometry and vectors The diagram shows two vectors that point west and north.
The diagram shows two vectors that point west and north. Composition of vectors
Composition of vectors Vectors and matrices
Vectors and matrices Collinear vector
Collinear vector Units physical quantities and vectors
Units physical quantities and vectors Chapter 1 physical quantities and measurement
Chapter 1 physical quantities and measurement Magnitude of unit vector formula
Magnitude of unit vector formula A student adds two vectors with magnitudes of 200 and 40
A student adds two vectors with magnitudes of 200 and 40 Fall vectors
Fall vectors You are adding vectors of length 20 and 40 units
You are adding vectors of length 20 and 40 units Parallel and perpendicular lines unit 3
Parallel and perpendicular lines unit 3 2-5 reasoning in algebra and geometry
2-5 reasoning in algebra and geometry Geometry statements and reasons
Geometry statements and reasons Axe notation chart
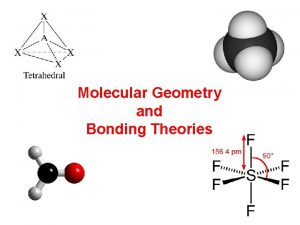
Axe notation chart Molecular geometry and bonding theories
Molecular geometry and bonding theories Bent lewis dot structure
Bent lewis dot structure Introduction to geometry points lines and planes
Introduction to geometry points lines and planes Adjacent vs perpendicular
Adjacent vs perpendicular Chapter 12 test geometry
Chapter 12 test geometry Chapter 9 conic sections and analytic geometry
Chapter 9 conic sections and analytic geometry Geometry statements and reasons
Geometry statements and reasons What is a minor arc
What is a minor arc Practice 8-4 sine and cosine ratios
Practice 8-4 sine and cosine ratios 2-5 think about a plan reasoning in algebra and geometry
2-5 think about a plan reasoning in algebra and geometry Geometry statements and reasons
Geometry statements and reasons Nets and drawings for visualizing geometry
Nets and drawings for visualizing geometry Deductive reasoning
Deductive reasoning Geometry greek meaning
Geometry greek meaning 6-6 practice trapezoids and kites
6-6 practice trapezoids and kites Ratios and proportions geometry
Ratios and proportions geometry Differences between deductive and inductive reasoning
Differences between deductive and inductive reasoning Ratios and proportions 7-1
Ratios and proportions 7-1 Geometry chapter 7 proportions and similarity answers
Geometry chapter 7 proportions and similarity answers Lesson 1 nets and drawings for visualizing geometry
Lesson 1 nets and drawings for visualizing geometry Geometric design of railway
Geometric design of railway Honors geometry parallel lines and transversals worksheet
Honors geometry parallel lines and transversals worksheet Proof parallel and perpendicular lines
Proof parallel and perpendicular lines