Graphing and Solving Systems of Linear Inequalities ACT

Graphing and Solving Systems of Linear Inequalities

ACT WARM-UP

Objectives Solve systems of inequalities by graphing Determine the coordinates of the vertices of a region formed by the graph of a system of inequalities.

Essential Question How do you determine the solution set of a system of inequalities?

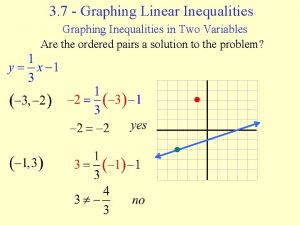
A short review on graphing inequalities. In order to graph the inequality y > 3 – x first graph the equation y = 3 – x. This line will be the borderline between the points that make y > 3 – x true and the points that make y < 3 – x true. In y = mx + b form we have y = -x + 3. In this case we have a line whose slope is – 1 and whose yintercept is 3. Now we have to decide which side of the line satisfies y > 3 – x.

A short review on graphing inequalities. All we have to do is to choose one point that is off the line and test it in the original inequality. If the point satisfies the inequality then we are on the correct side of the line and we shade that side. If the point does not satisfy the line, we shade the other side. The most popular point to use in the shading test is (0, 0) if it is not on the line. THE TEST: substitute (0, 0) into y > 3 – x and see if you get a true statement. 0>3 -0 0 > 3, which is false.

Since (0, 0) did not satisfy the inequality y > 3 – x we conclude that (0, 0) is on the wrong side of the tracks and we shade the other side. Our conclusion is that every point in the shaded area is part of the solution set for y > 3 – x. You can reinforce this idea by testing several points in the shaded area. (2, 2) 2>3– 2 2>1 (0, 3) 3>3– 0 3>3 (4, 1) 1>3– 4 1 > -1 Each point that we pick in the shaded area generates a true statement.

Steps for Graphing 1. Graph the lines and appropriate shading for each inequality on the same coordinate plane. 2. Be sure to pay attention to whether the lines are dotted or solid. 3. The final shaded area is the section where all the shadings overlap. * Sometimes it helps to use a different colored pencil for each line and shaded region. It makes it easier to determine the overlapped shaded regions.

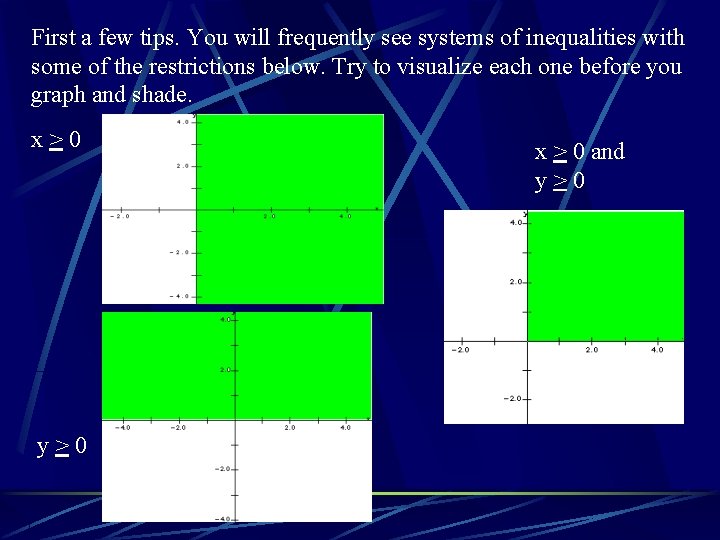
First a few tips. You will frequently see systems of inequalities with some of the restrictions below. Try to visualize each one before you graph and shade. x>0 y>0 x > 0 and y>0

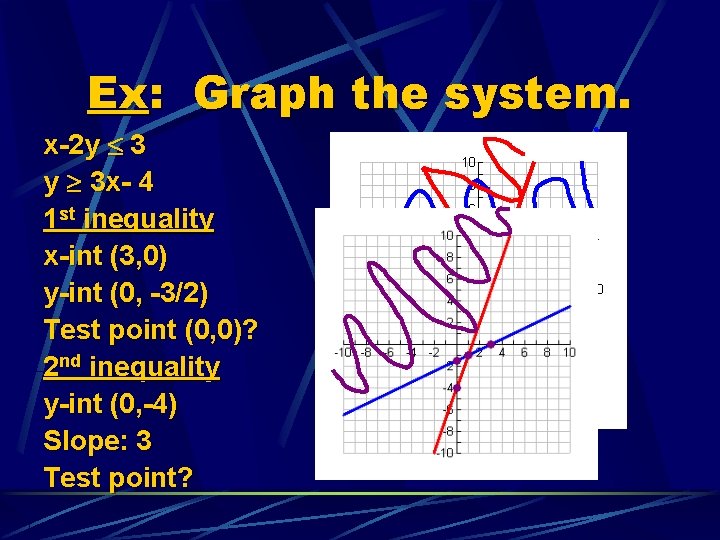
Ex: Graph the system. x-2 y 3 x- 4 1 st inequality x-int (3, 0) y-int (0, -3/2) Test point (0, 0)? 2 nd inequality y-int (0, -4) Slope: 3 Test point?

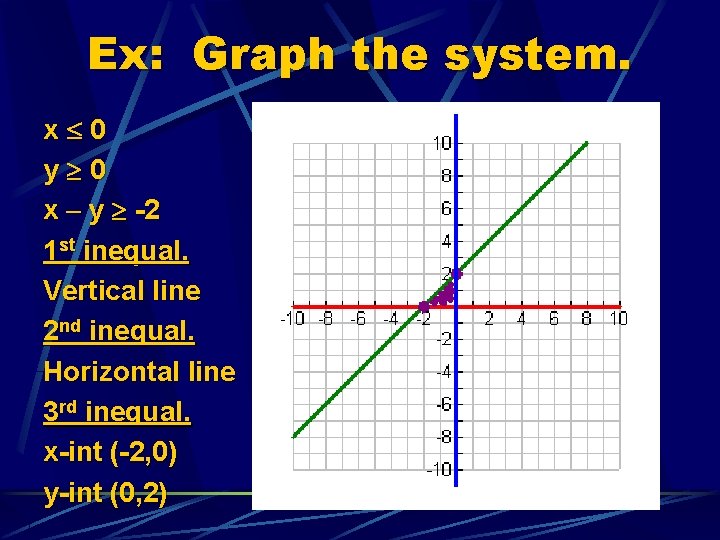
Ex: Graph the system. x 0 y 0 x – y -2 1 st inequal. Vertical line 2 nd inequal. Horizontal line 3 rd inequal. x-int (-2, 0) y-int (0, 2)

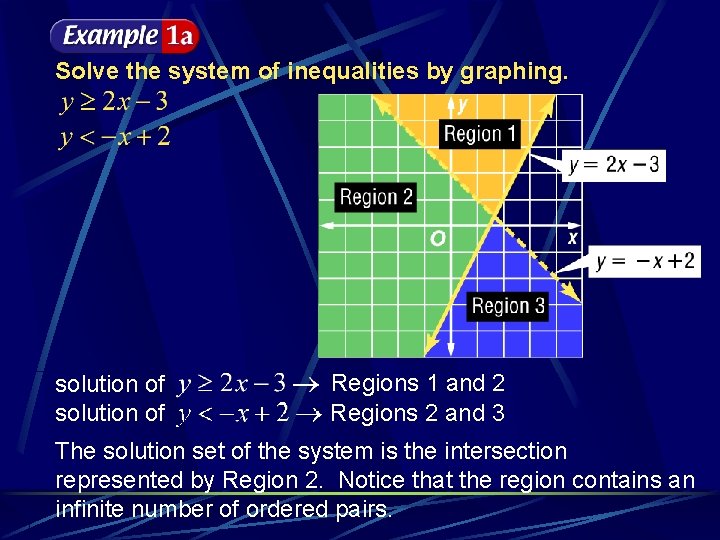
Solve the system of inequalities by graphing. solution of Regions 1 and 2 Regions 2 and 3 The solution set of the system is the intersection represented by Region 2. Notice that the region contains an infinite number of ordered pairs.

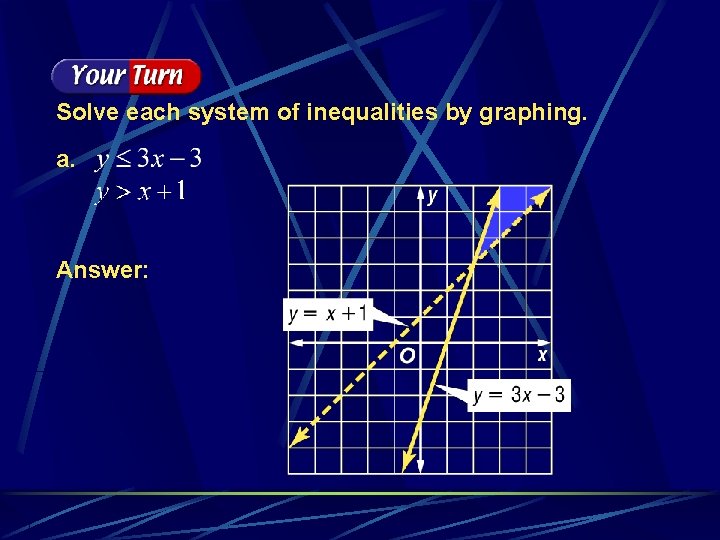
Solve each system of inequalities by graphing. a. Answer:

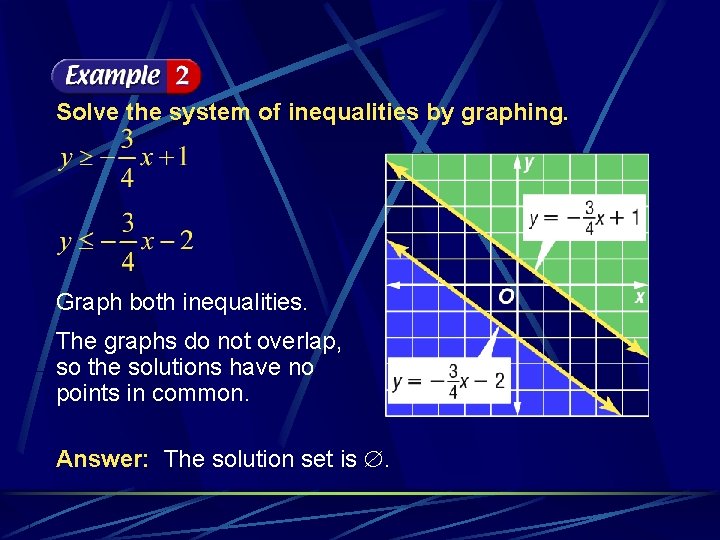
Solve the system of inequalities by graphing. Graph both inequalities. The graphs do not overlap, so the solutions have no points in common. Answer: The solution set is .

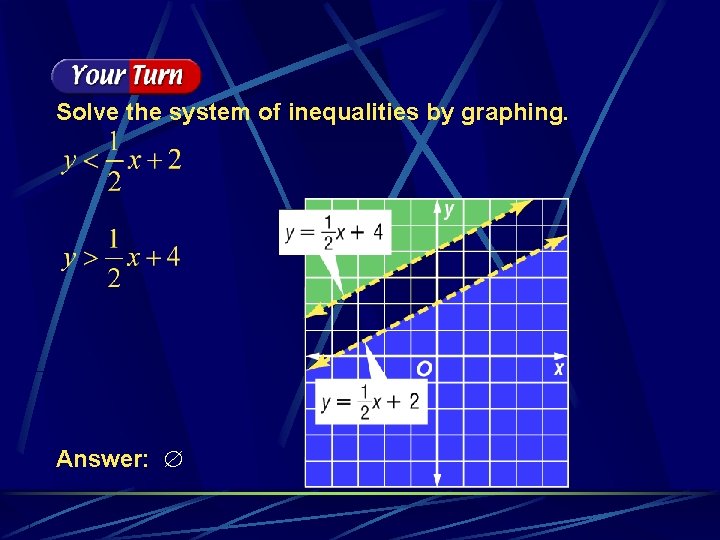
Solve the system of inequalities by graphing. Answer:

Find the coordinates of the vertices of the figure formed by and Graph each inequality. The intersection of the graphs forms a triangle. Answer: The vertices of the triangle are at (0, 1), (4, 0), and (1, 3).

If a vertex cannot be determined by graphing, solve the system of equations algebraically that form the intersection. Previous example: Find the coordinates of the vertices of the figure formed by and Let be equation #1, equation #2, and equation #3 will be Solve by elimination to get (1, 3) for the intersection of #1 and #2. Do the same for the intersections of equations #1 and #3 for (0, 1), and equations #2 and #3 for the point (4, 0).

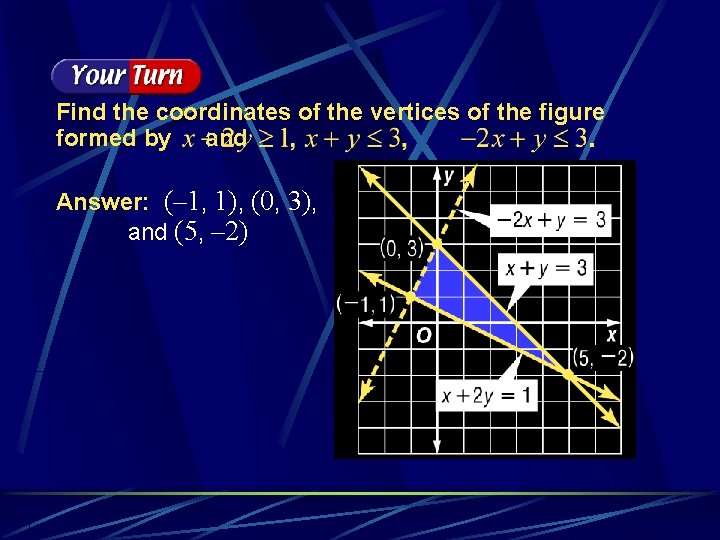
Find the coordinates of the vertices of the figure formed by and Answer: (– 1, 1), (0, 3), and (5, – 2)

Essential Question How do you determine the solution set of a system of inequalities? Graph the inequalities on the same coordinate plane. The solution set is represented by the intersection of the graphs.

Math Humor Why didn’t the chicken cross to the other side of the inequality? It couldn’t get past the boundary line.