Square Roots and Solving Quadratics with Square Roots



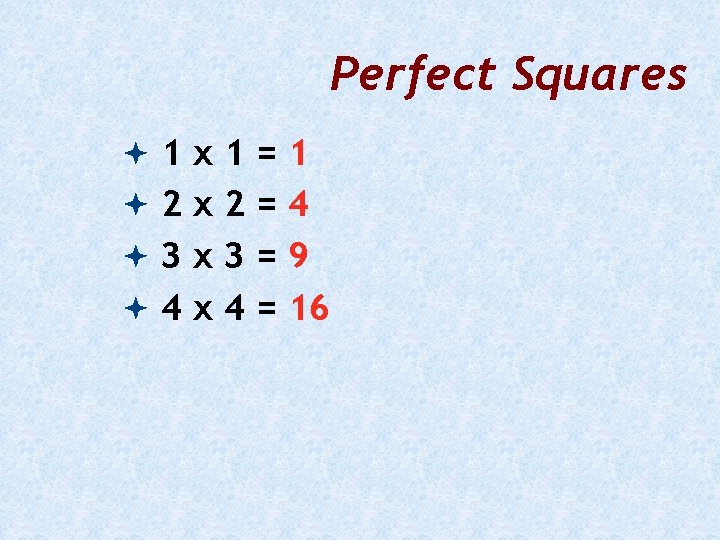

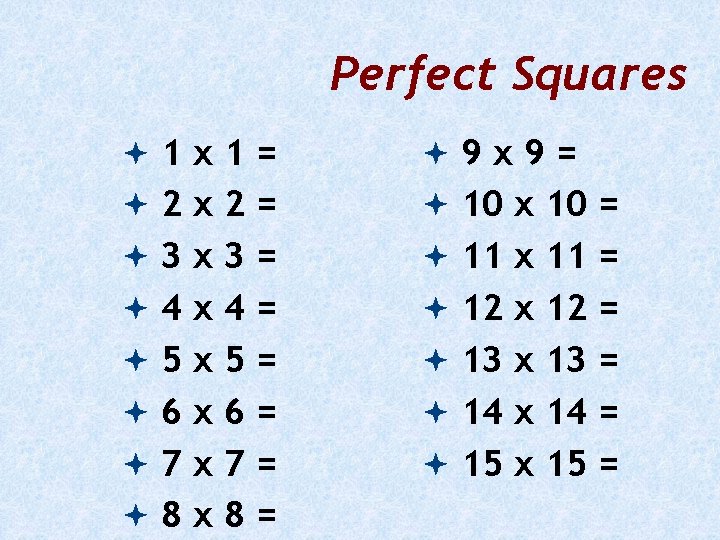



























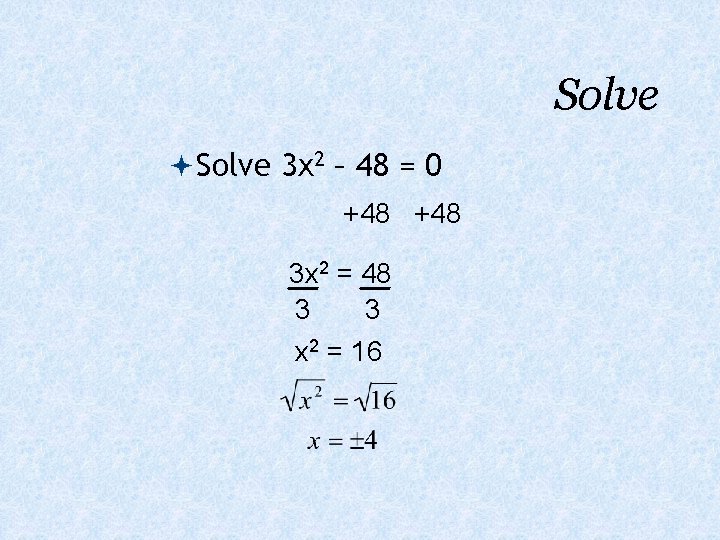
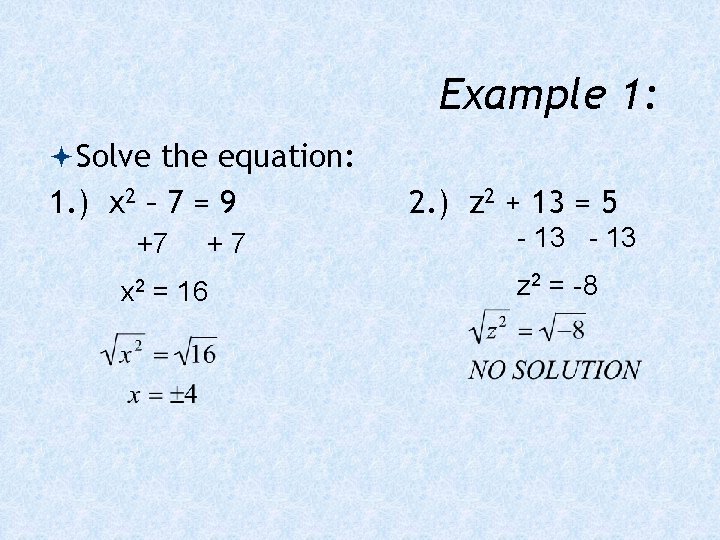

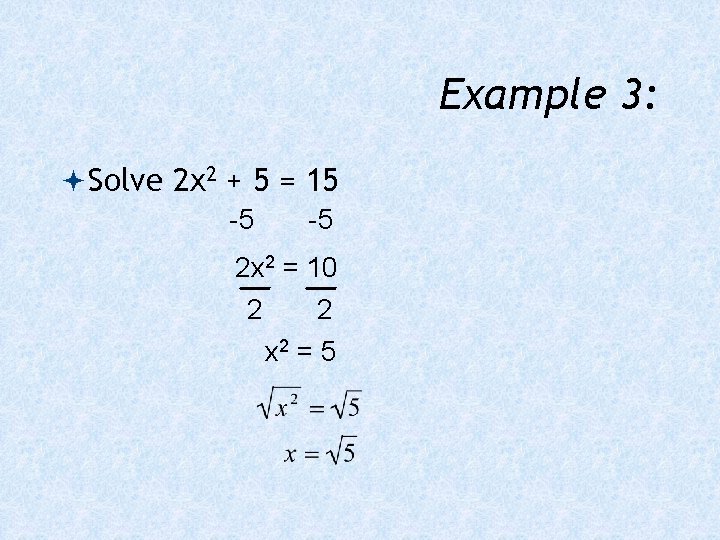
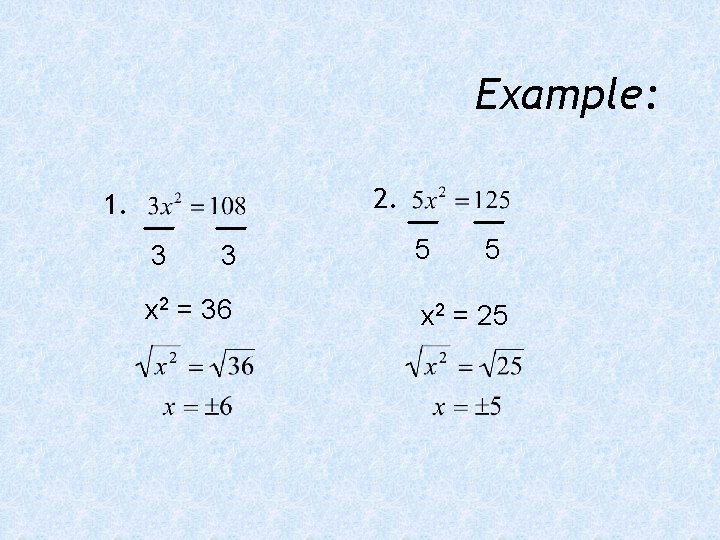
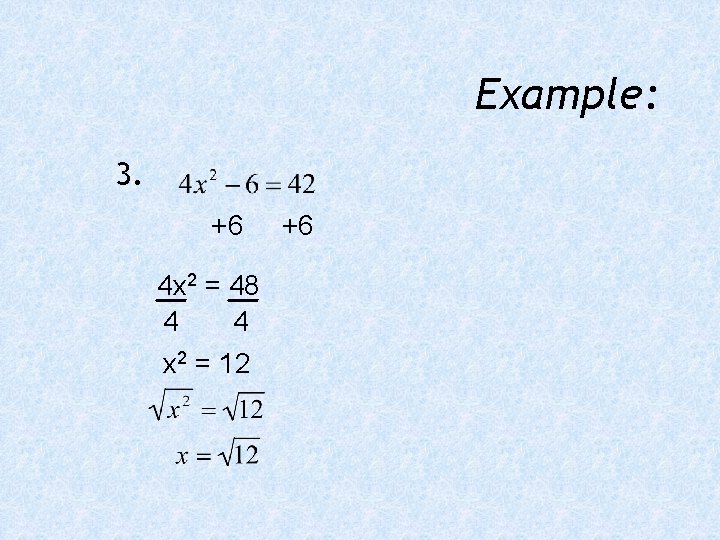
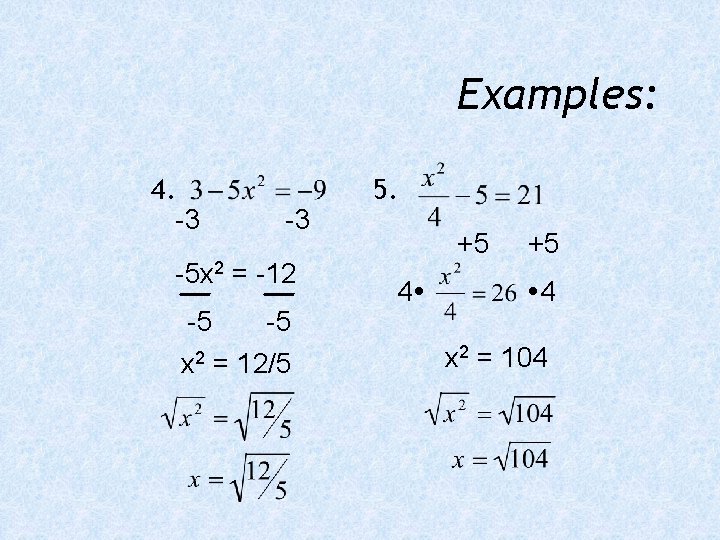
- Slides: 44

Square Roots and Solving Quadratics with Square Roots 1. 4

GET YOUR COMMUNICATORS!!!!

Warm Up Simplify. 1. 52 25 2. 82 3. 122 144 4. 152 5. 202 400 64 225

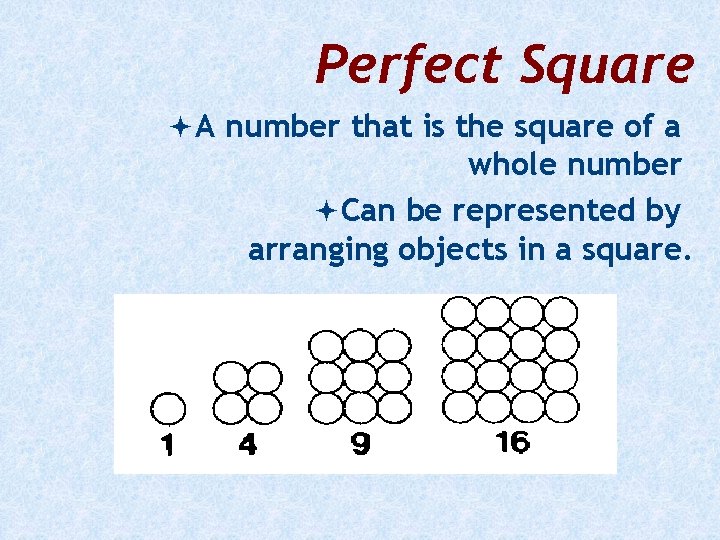
Perfect Square A number that is the square of a whole number Can be represented by arranging objects in a square.

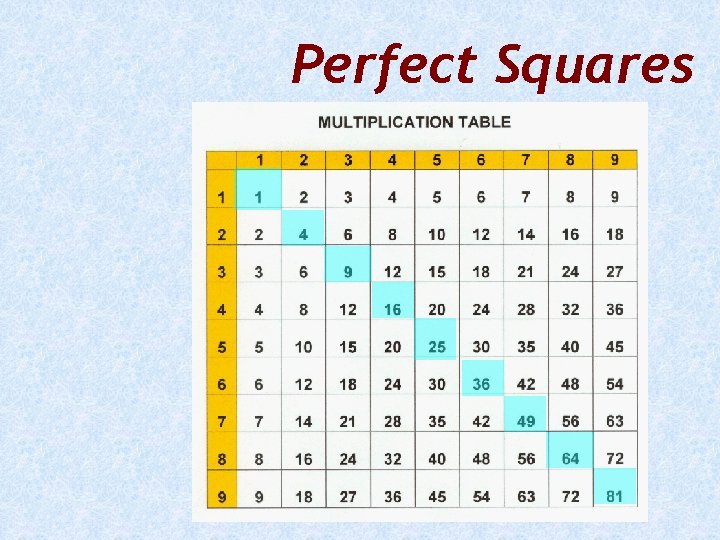
Perfect Squares
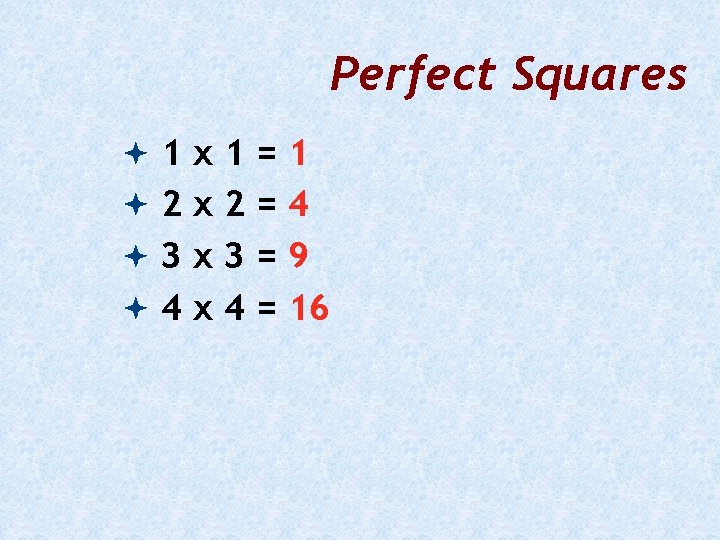
Perfect Squares 1 x 1=1 2 x 2=4 3 x 3=9 4 x 4 = 16

Perfect Squares 1 x 1=1 2 x 2=4 3 x 3=9 4 x 4 = 16 Activity: Calculate the perfect squares up to 152…
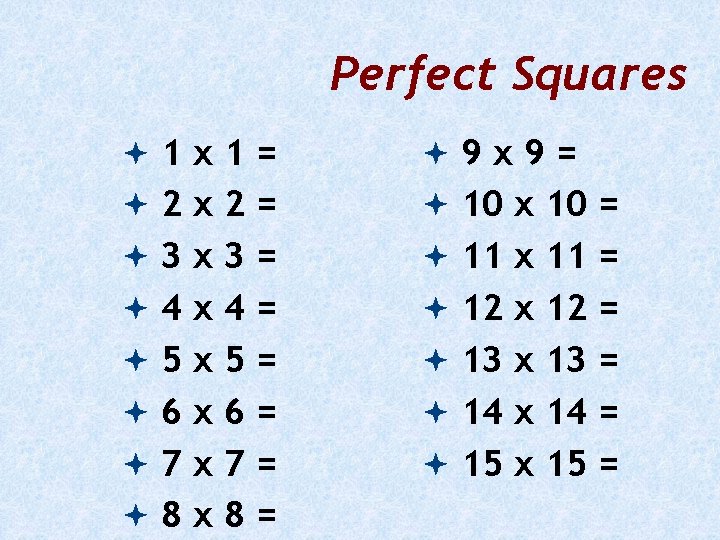
Perfect Squares 1 x 1= 9 x 9= 2 x 2= 10 x 10 = 3 x 3= 11 x 11 = 4 x 4= 12 x 12 = 5 x 5= 13 x 13 = 6 x 6= 14 x 14 = 7 x 7= 15 x 15 = 8 x 8=

Activity: Identify the following numbers as perfect squares or not. 16 ii. 15 iii. 146 iv. 300 v. 324 vi. 729 i.

Activity: Identify the following numbers as perfect squares or not. 16 = 4 x 4 ii. 15 iii. 146 iv. 300 v. 324 = 18 x 18 vi. 729 = 27 x 27 i.

Perfect Squares: Numbers whose square roots are integers or quotients of integers.

video perfect squares and cubes video math mashup https: //www. youtube. com/watch? v=BSfvry_h 3 Q

Perfect Squares One property of a perfect 4 cm 16 cm 2 square is that it can be represented by a square array. Each small square in the array shown has a side length of 1 cm. The large square has a side length of 4 cm.

Perfect Squares The large square has an area of 4 cm x 4 cm = 16 cm 2. 4 cm 16 cm 2 The number 4 is called the square root of 16. We write: 4 = 16

Square Root A number which, when multiplied by itself, results in another number. Ex: 5 is the square root of 25. 5 = 25

Finding Square Roots We can think “what” times “what” equals the larger number. 36 = ___ x ___ Is there another answer? SO ± 6 IS THE SQUARE ROOT OF 36

Finding Square Roots We can think “what” times “what” equals the larger number. 256 = ___ x ___ Is there another answer? SO ± 16 IS THE SQUARE ROOT OF 256

Estimating Square Roots 25 = ?

Estimating Square Roots 25 = ± 5

Estimating Square Roots - 49 = ?

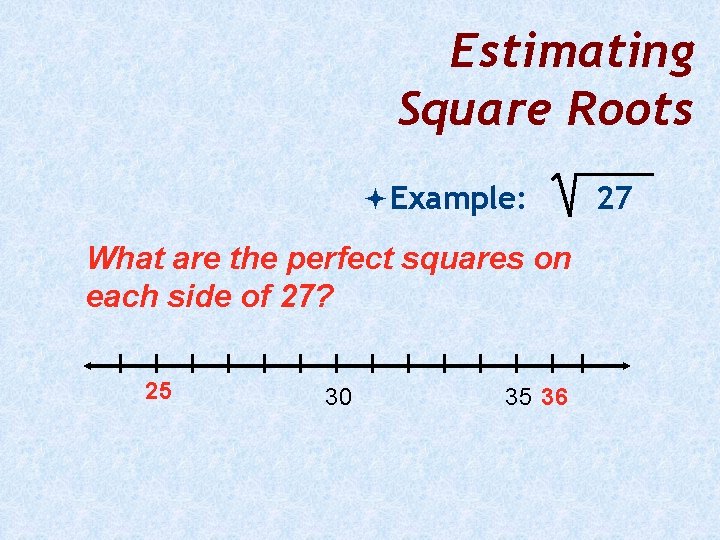
Estimating Square Roots 27 = ?

Estimating Square Roots 27 = ? Since 27 is not a perfect square, we will leave it in a radical because that is an EXACT ANSWER. If you put in your calculator it would give you 5. 196, which is a decimal apporximation.

Estimating Square Roots Not all numbers are perfect squares. Not every number has an Integer for a square root. We have to estimate square roots for numbers between perfect squares.

Estimating Square Roots To calculate the square root of a non-perfect square 1. Place the values of the adjacent perfect squares on a number line. 2. Interpolate between the points to estimate to the nearest tenth.

Estimating Square Roots Example: What are the perfect squares on each side of 27? 25 30 35 36 27

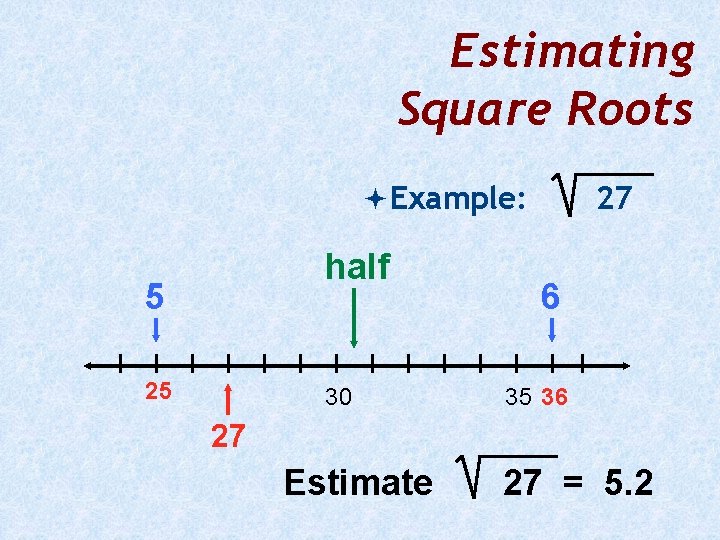
Estimating Square Roots Example: half 5 25 30 27 6 35 36 27 Estimate 27 = 5. 2

Estimating Square Roots Example: Estimate: 27 = 5. 2 Check: (5. 2) = 27. 04 27

Find the two square roots of each number. A. 49 7 is a square root, since 7 • 7 = 49. 49 = 7 49 = – 7 is also a square root, since – 7 • – 7 = 49. B. 100 = 10 10 is a square root, since 10 • 10 = 100 = – 10 is also a square root, since – 10 • – 10 = 100. C. 225 = 15 15 is a square root, since 15 • 15 = 225 = – 15 is also a square root, since – 15 • – 15 = 225.

Find the two square roots of each number. A. 25 25 = – 5 B. 144 = 12 5 is a square root, since 5 • 5 = 25. – 5 is also a square root, since – 5 • – 5 = 25. 12 is a square root, since 12 • 12 = 144 = – 12 is also a square root, since – 12 • – 12 = 144. C. 289 = 17 17 is a square root, since 17 • 17 = 289 = – 17 is also a square root, since – 17 • – 17 = 289.


Evaluate a Radical Expression EXAMPLE SHOWN BELOW

Evaluate a Radical #1 Expression

Evaluate a Radical #2 Expression

Evaluate a Radical #3 Expression

Evaluate a Radical #4 Expression

SOLVING EQUATIONS SOLVING MEANS “ISOLATE” THE VARIABLE x = ? ? ? y = ? ? ?

Solving quadratics Solve each equation. a. x 2 = 4 b. x 2 = 5 SQUARE ROOT BOTH SIDES c. x 2 = 0 d. x 2 = -1
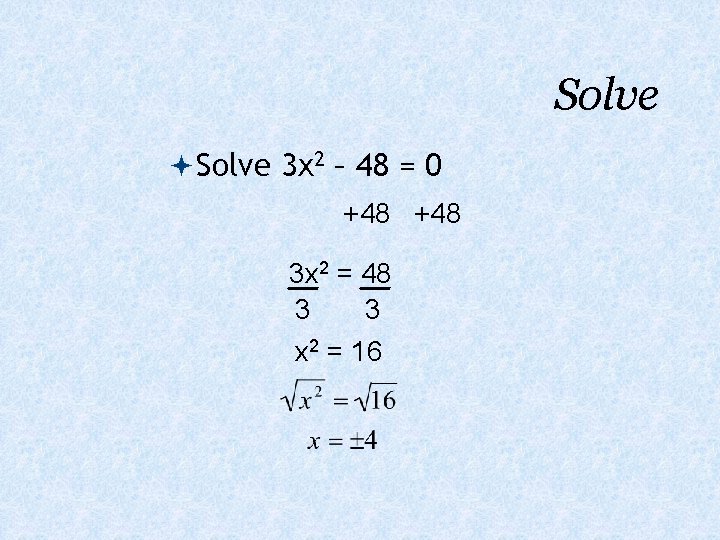
Solve 3 x 2 – 48 = 0 +48 3 x 2 = 48 3 3 x 2 = 16
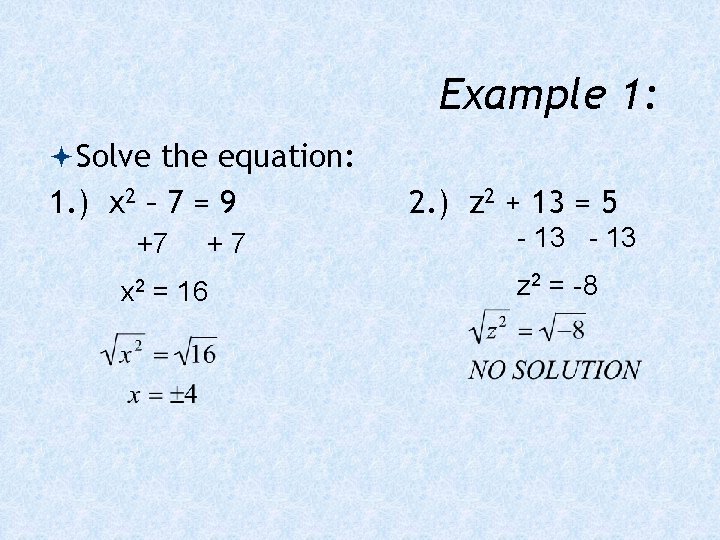
Example 1: Solve the equation: 1. ) x 2 – 7 = 9 +7 x 2 +7 = 16 2. ) z 2 + 13 = 5 - 13 z 2 = -8

Example 2: Solve 9 m 2 = 169 9 m 2 = 9
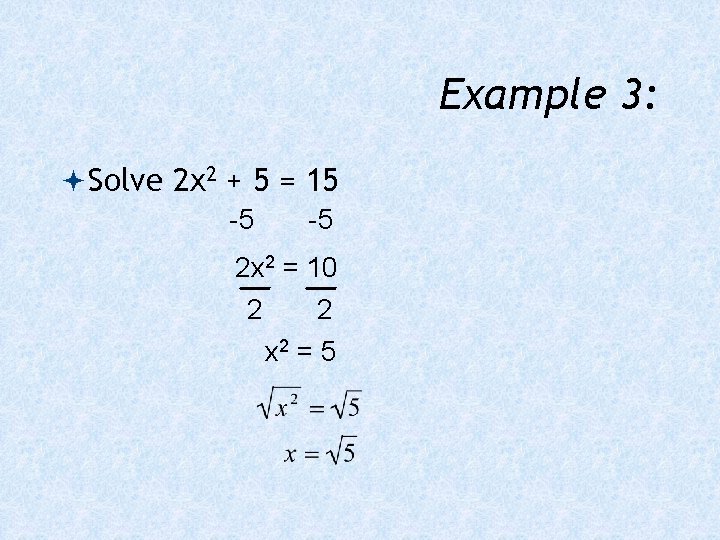
Example 3: Solve 2 x 2 + 5 = 15 -5 -5 2 x 2 = 10 2 2 x 2 = 5
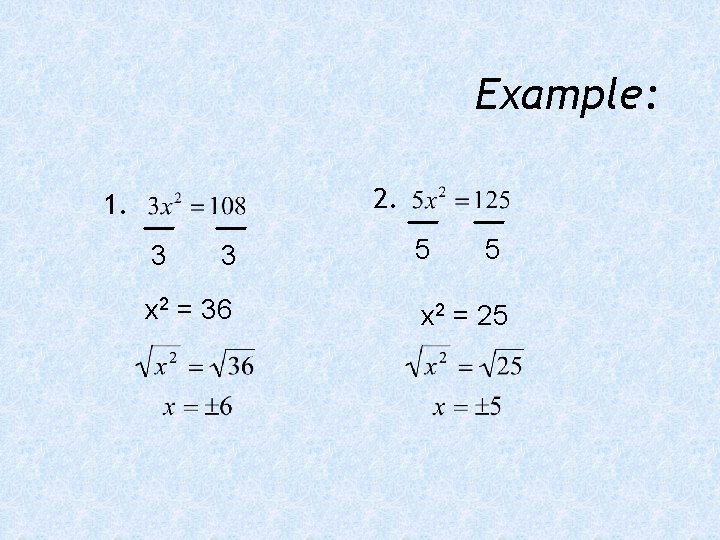
Example: 2. 1. 3 3 x 2 = 36 5 5 x 2 = 25
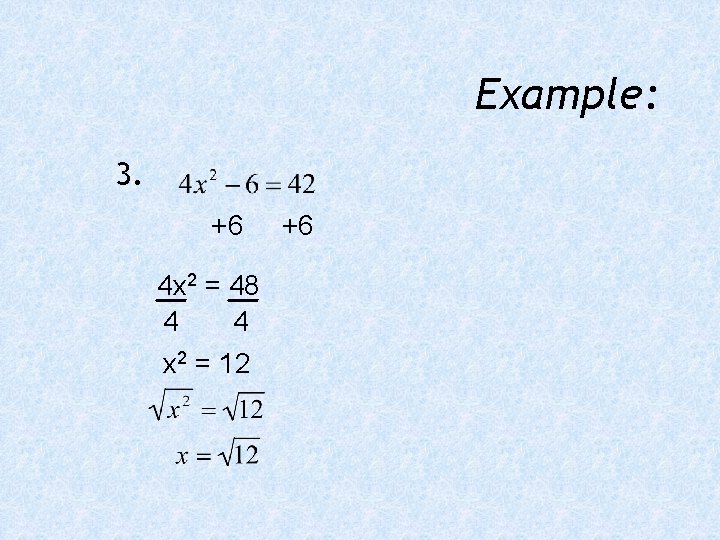
Example: 3. +6 4 x 2 = 48 4 4 x 2 = 12 +6
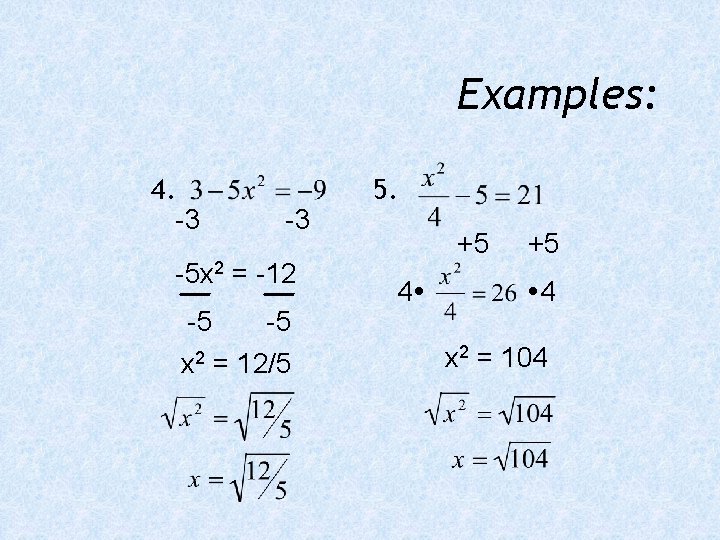
Examples: 4. -3 -3 -5 x 2 = -12 -5 -5 x 2 = 12/5 5. +5 4 x 2 = 104