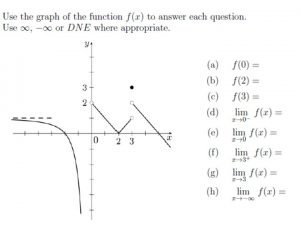
Solving Systems of Equations Algebraically Substitution Method The

Solving Systems of Equations Algebraically Substitution Method

The substitution method is used to eliminate one of the variables by replacement when solving a system of equations. Think of it as “grabbing” what one variable equals from one equation and “plugging” it into the other equation.

Solve this system of equations using the substitution method. Step 1 3 y – 2 x = 11 Y + 2 x = 9 Solve one of the equations for either “x” or “y”. In this example it is easier to solve the second equation for “y”, since it only involves one step. Y = 9 – 2 x

Step 2 Replace the “y” value in the first equation by what “y” now equals (y = 9 – 2 x). Grab the “y” value and plug it into the other equation. 3 y – 2 x = 11 3(9 – 2 x) – 2 x = 11

Step 3 Solve this new equation for “x”. 3(9 – 2 x) – 2 x = 11 27 – 6 x – 2 x = 11 27 – 8 x = 11 -8 x = -16 x=2

Step 4 Now that we know the “x” value (x = 2), we place it into either of the ORIGINAL equations in order to solve for “y”. Pick the easier one to work with! Y + 2 x = 9 y + 2(2) = 9 y+4=9 y=5

Step 5 Check: substitute x = 2 and y = 5 into BOTH ORIGINAL equations. If these answers are correct BOTH equations will be true! 3 y – 2 x = 11 3(5) – 2(2) = 11 15 – 4 = 11 11 = 11 True? Y + 2 x = 9 5 + 2(2) = 9 5+4=9 9 = 9 True?

The Substitution Method • Step 1 Solve one equation for x (or y). • Step 2 Substitute the expression from Step 1 into the other equation. • Step 3 Solve for y (or x). • Step 4 Take the value of y (or x) found in Step 3 and substitute it into one of the original equations. Then solve for the other variable. • Step 5 The ordered pair of values from Steps 3 and 4 is the solution. If the system has no solution, a contradictory statement will result in either Step 3 or 4.

Use the substitution method to solve each system of equations. Check your answers.

Solving systems of equations in real-world problems. April sold 75 tickets to a school play and collected a total of $495. If the adult tickets cost $8 each and child tickets cost $5 each, how many adult tickets and how many child tickets did she sell? Solution: Let a represent the adult tickets and c represent the child tickets. Individual tickets sold equaled 75, so a + c = 75 All total April sold $495 in tickets, since adult tickets are $8 and child tickets are $5, so 8 a + 5 c = 495. System of Equations a + c = 75 8 a + 5 c == 495

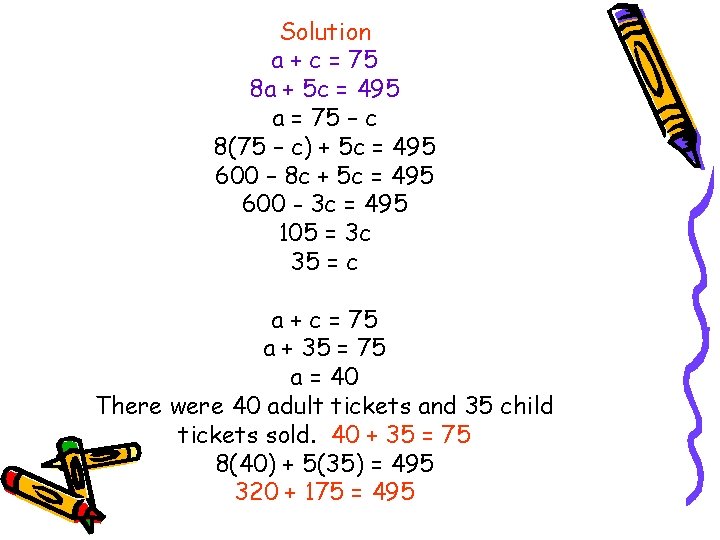
Solution a + c = 75 8 a + 5 c = 495 a = 75 – c 8(75 – c) + 5 c = 495 600 – 8 c + 5 c = 495 600 - 3 c = 495 105 = 3 c 35 = c a + c = 75 a + 35 = 75 a = 40 There were 40 adult tickets and 35 child tickets sold. 40 + 35 = 75 8(40) + 5(35) = 495 320 + 175 = 495

Write a system of equations and solve. At a baseball game, Jose bought five hot dogs and three sodas for $17. At the same time, Allison bought two hot dogs and four sodas for $11. Find the cost of one hot dog and one soda.

Solving Systems of Equations Elimination method

You can use the Addition and Subtraction Properties of Equality to solve a system by the elimination method. You can add or subtract equations to eliminate (getting rid of) a variable. If you add the two equations Step 1 together, the +6 y and -6 y each other out because 5 x – 6 y = -32 cancel of the Property of Additive Inverse 3 x + 6 y = 48 Eliminate y because the sum of the coefficients of y is zero 5 x – 6 y = -32 3 x + 6 y = 48 8 x + 0 = 16 Addition Property of Equality Solve for x x = 2

Step 2 Solve for the eliminated variable y using either of the original equations. Remember x = 2 3 x + 6 y = 48 3(2) + 6 y = 48 6 y = 42 y = 7 Choose the 2 nd equation Substitute 2 for x Simplify. Then solve for y.

Since x = 2 and y = 7, the solution is (2, 7) Check 5 x – 6 y = -32 3 x + 6 y = 48 5(2) – 6(7) = -32 3(2) + 6(7) = 48 10 – 42 = -32 6 + 42 = 48 -32 = -32 48 = 48 True Remember, the order pair (2, 7) must make both equations true.

Suppose your community center sells a total of 292 tickets for a basketball game. An adult ticket cost $3. A student ticket cost $1. The sponsors collected $470 in ticket sales. Write and solve a system to find the number of each type of ticket sold.

Let a = number of adult tickets Let s = number of student tickets total number of ticket total number of sales a + s = 292 3 a + 1 s = 470 Solve by elimination (get rid of s) because the difference of the coefficients of s is zero. a + s = 292 3 a + s = 470 This is the number That means you must subtract of adult tickets -2 a + 0 = -178 the two equations so, sold. -3 a – a = -470 is what you must a = 89 subtract. Next Step

Solve for the eliminated variable using either of the original equations. This is the number of student tickets sold. a + s = 292 89 + s = 292 s = 203 There were 89 adult tickets sold and 203 student tickets sold. Is the solution reasonable? The total number of tickets is 89 + 203 = 292. The total sales is $3(89) + $1(203) = $470. The solution is correct.

If you have noticed in the last few examples that to eliminate a variable its coefficients must have a sum or difference of zero. Sometime you may need to multiply one or both of the equations by a nonzero number first so that you can then add or subtract the equations to eliminate one of the We can add these two equations We can add these two variables. together to eliminate the y variable. 2 x + 5 y = 17 6 x – 5 y = -19 equations together to eliminate the x variable. 7 x + 2 y = 10 -7 x + y = -16 2 x + 5 y = -22 10 x + 3 y = 22 If you notice the systems of equations above, two of them have something in common. The third doesn’t. What are we going to do with these equations, can’t eliminate a variable the way they are written?

Multiplying One Equation Be careful when you subtract. All the signs in the equation that is being subtracted change. -10 x – 3 y = -22 Solve by Elimination 2 x + 5 y = -22 10 x + 3 y = 22 Start with the given system. Step 1 2 x + 5 y = -22 10 x + 3 y = 22 To prepare for eliminating x, multiply the first equation by 5. 5(2 x + 5 y = -22) 10 x + 3 y = 22 Ask: Is one coefficient a factor of the other coefficient for the same variable? Subtract the equations to eliminate x. 10 x + 25 y = -110 -(10 x + 3 y = 22) 0 + 22 y = -132 y = -6 NEXT

Step 2 Solve for the eliminated variable using either of the original equations. 2 x + 5 y = -22 2 x +5(-6) = -22 2 x – 30 = -22 2 x = 8 x=4 Choose the first equation. Substitute -6 for y. Solve for x. The solution is (4, -6).

Solve by elimination. -2 x + 5 y = -32 7 x – 5 y = 17 3 x – 10 y = -25 4 x + 40 y = 20 2 x – 3 y = 61 2 x + y = -7 Ask: Is one coefficient a factor of the other coefficient for the same variable?

Multiplying Both Equations To eliminate a variable, you may need to multiply both equations in a system by a nonzero number. Multiply each equation by values such that when you write equivalent equations, you can then add or subtract to eliminate a variable. In these two equations you cannot use graphing or substitution very easily. However if we multiply the first equation by 3 and the second by 2, we can eliminate the y variable. 4 x + 2 y = 14 7 x + 3 y = -8 4 x 7 = 28 2 x 3=6 Find the least common multiple LCM of the coefficients of one variable, since working with smaller numbers tends to reduce the likelihood of errors. NEXT

Add the equations to eliminate y. 4 X + 2 Y = 14 7 X – 3 Y = - 8 Start with the given system. 3(4 X + 2 Y = 14) 2(7 X – 3 Y = -8) 12 X + 6 Y = 42 14 X – 6 Y = -16 26 X + 0 = 26 To prepare to eliminate y, multiply the first equation by 3 and the second equation by 2. 26 X = 26 X = 1 Solve for the eliminated variable y using either of the original equations. 4 x + 2 y = 14 4(1) + 2 y = 14 4 + 2 y = 14 2 y = 10 y= 5 The solution is (1, 5).

Practice and Problem Solving Solve by elimination: 1) 2 x + 5 y = 17 6 x + 5 y = -9 2) 7 x + 2 y = 10 -7 x + y = -16 3) 2 x – 3 y = 61 2 x + y = -7 4) 24 x + 2 y = 52 6 x – 3 y = -36 5) y = 2 x y=x– 1 You choose what method you what to use to solve question 5 thru 10. 6) 9 x + 5 y = 34 8 x – 2 y = -2 Word Problems

7) The sum of two numbers is 20. Their difference is 4. Write and solve a system of equations. 8) Your school sold 456 tickets for a school play. An adult ticket cost $3. 50. A student ticket cost $1. Total ticket sales equaled $1131. Let a = adult tickets sold, and s = student tickets sold. How many tickets of each were sold? 9) Suppose the band sells cans of popcorn for $5 each and mixed nuts for $8 each. The band sells a total of 240 cans and makes a total of $1614. Find the number of cans of each sold. One more problem, my favorite.

10) A farmer raises chicken and cows. He has a total of 34 animals in his barnyard. His sixyear son came in one day all excited saying, “Daddy, did you know all your animals have a total of 110 legs. ” Write a system of equations to represent this situation. How many chickens and how many cows does the farmer have?

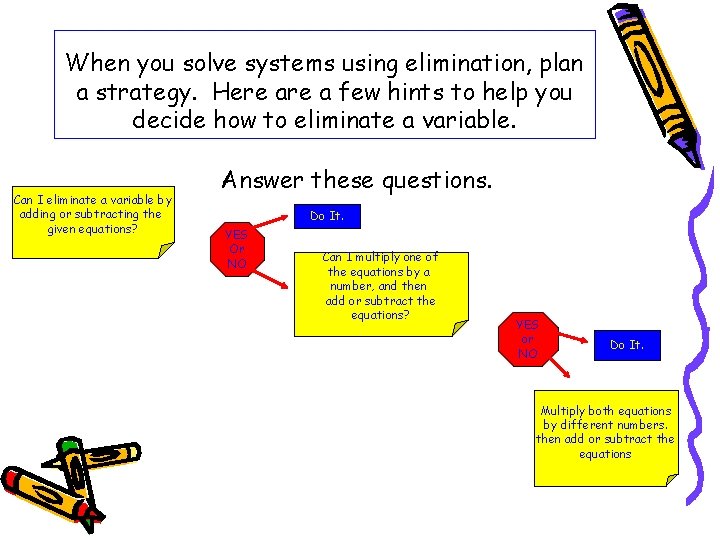
When you solve systems using elimination, plan a strategy. Here a few hints to help you decide how to eliminate a variable. Can I eliminate a variable by adding or subtracting the given equations? Answer these questions. Do It. YES Or NO Can I multiply one of the equations by a number, and then add or subtract the equations? YES or NO Do It. Multiply both equations by different numbers. then add or subtract the equations