Solving Systems of Equations using Elimination Steps 1

NOW solve these using elimination: 1. 2 x + 4 y =1 x -

Using Elimination to Solve a Word Problem: Two angles are supplementary. The measure of

Using Elimination to Solve a Word Problem: Solve x + y = 180 x

Using Elimination to Solve a Word Problem: The sum of two numbers is 70

Using Elimination to Solve a Word Problem: x + y =70 x - y

Slides: 17

Download presentation

Solving Systems of Equations using Elimination Steps: 1. Place both equations in Standard Form, Ax + By = C. 2. Determine which variable to eliminate with Addition or Subtraction. 3. Solve for the variable left. 4. Go back and use the found variable in step 3 to find second variable. 5. Check the solution in both equations of the system.

EXAMPLE #1: 5 x + 3 y = 11 5 x = 2 y + 1 STEP 1: Write both equations in Ax + By = C form. 5 x + 3 y =1 5 x - 2 y =1 STEP 2: Use subtraction to eliminate 5 x. 5 x + 3 y =11 5 x + 3 y = 11 -(5 x - 2 y =1) Note: the -5 x(-)+ is 2 ydistributed. = -1 STEP 3: Solve for the variable. 5 x + 3 y =11 -5 x + 2 y = -1 5 y =10 y=2

5 x + 3 y = 11 5 x = 2 y + 1 STEP 4: Solve for the other variable by substituting into either equation. 5 x + 3 y =11 5 x + 3(2) =11 5 x + 6 =11 5 x = 5 x=1 The solution to the system is (1, 2).

5 x + 3 y= 11 5 x = 2 y + 1 Step 5: Check the solution in both equations. The solution to the system is (1, 2). 5 x + 3 y = 11 5(1) + 3(2) =11 5 + 6 =11 11=11 5 x = 2 y + 1 5(1) = 2(2) + 1 5=4+1 5=5

Solving Systems of Equations using Elimination Steps: 1. Place both equations in Standard Form, Ax + By = C. 2. Determine which variable to eliminate with Addition or Subtraction. 3. Solve for the remaining variable. 4. Go back and use the variable found in step 3 to find the second variable. 5. Check the solution in both equations of the system.

Example #2: x + y = 10 5 x – y = 2 Step 1: The equations are already in standard form: x + y = 10 5 x – y = 2 Step 2: Adding the equations will eliminate y. x + y = 10 +(5 x – y = 2) +5 x – y = +2 Step 3: Solve for the variable. x + y = 10 +5 x – y = +2 6 x = 12 x=2

x + y = 10 5 x – y = 2 Step 4: Solve for the other variable by substituting into either equation. x + y = 10 2 + y = 10 y=8 Solution to the system is (2, 8).

x + y = 10 5 x – y = 2 Step 5: Check the solution in both equations. Solution to the system is (2, 8). x + y =10 2 + 8 =10 10=10 5 x – y =2 5(2) - (8) =2 10 – 8 =2 2=2

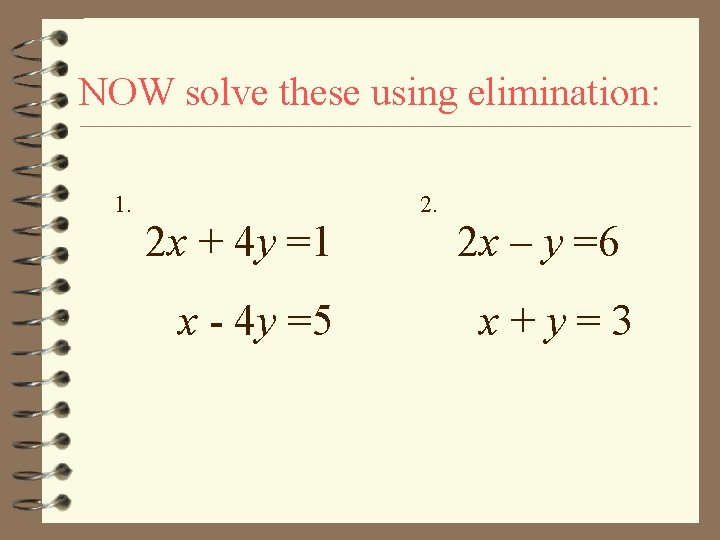
NOW solve these using elimination: 1. 2 x + 4 y =1 x - 4 y =5 2 x – y =6 x+y=3

Using Elimination to Solve a Word Problem: Two angles are supplementary. The measure of one angle is 10 degrees more than three times the other. Find the measure of each angle.

Using Elimination to Solve a Word Problem: Two angles are supplementary. The measure of one angle is 10 more than three times the other. Find the measure of each angle. x = degree measure of angle #1 y = degree measure of angle #2 Therefore x + y = 180

Using Elimination to Solve a Word Problem: Two angles are supplementary. The measure of one angle is 10 more than three times the other. Find the measure of each angle. x + y = 180 x =10 + 3 y

Using Elimination to Solve a Word Problem: Solve x + y = 180 x =10 + 3 y x + y = 180 -(x - 3 y = 10) 4 y =170 y = 42. 5 x + 42. 5 = 180 x = 180 - 42. 5 x = 137. 5 (137. 5, 42. 5)

Using Elimination to Solve a Word Problem: The sum of two numbers is 70 and their difference is 24. Find the two numbers.

Using Elimination to Solve a Word problem: The sum of two numbers is 70 and their difference is 24. Find the two numbers. x = first number y = second number Therefore, x + y = 70

Using Elimination to Solve a Word Problem: The sum of two numbers is 70 and their difference is 24. Find the two numbers. x + y = 70 x – y = 24

Using Elimination to Solve a Word Problem: x + y =70 x - y = 24 2 x = 94 x = 47 47 + y = 70 – 47 y = 23 (47, 23)