Use factoring to solve the quadratic equation x






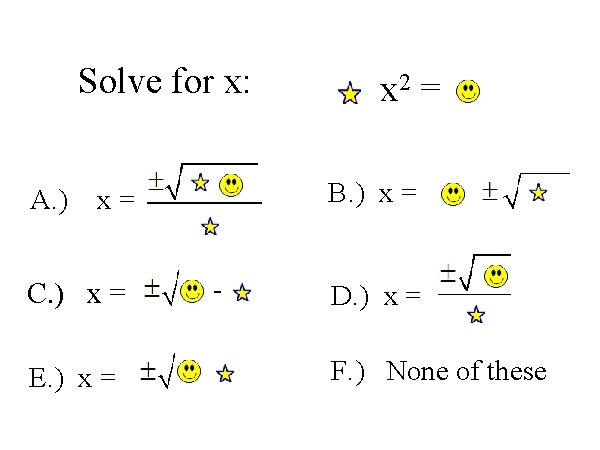
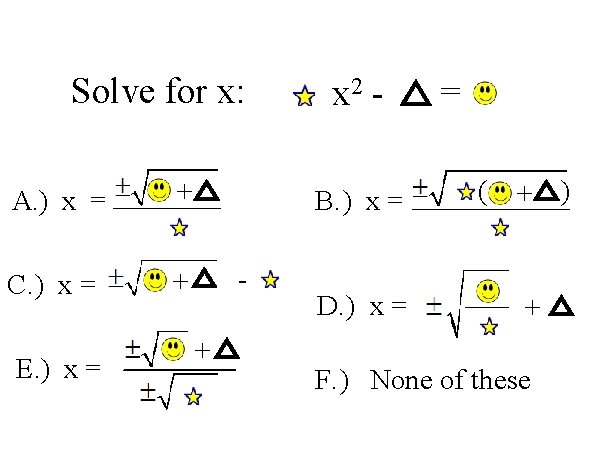

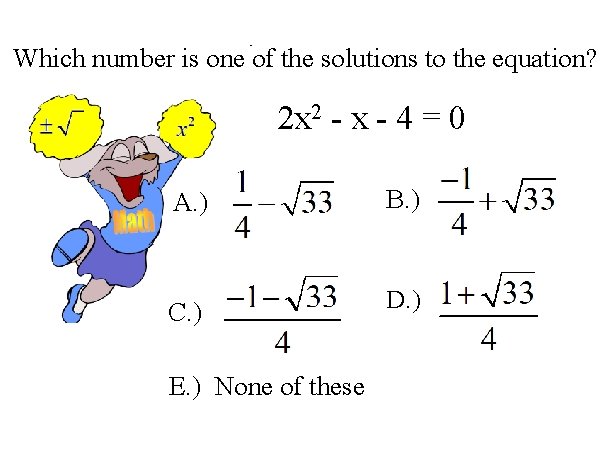

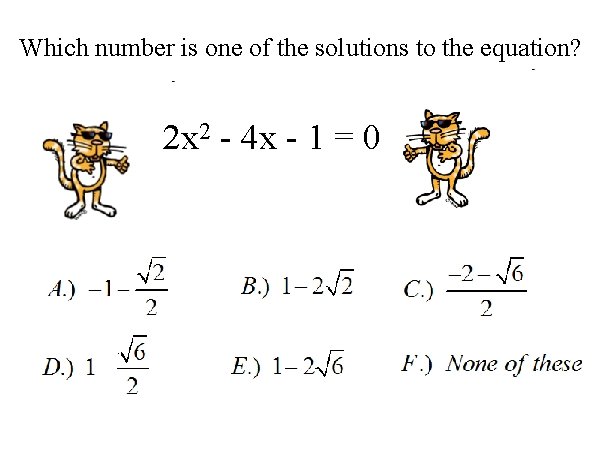



- Slides: 15

Use factoring to solve the quadratic equation. x 2 - 4 x = 32 The sum of the solutions is: A. ) 12 B. ) 4 C. ) -12 F. ) None of these D. ) -4 E. ) 0

Solve by factoring: (x+2)(x-1) = 4 The sum of the solutions is: A. ) 1 B. ) -5 C. ) -2 D. ) 5 E. ) -1 F. ) None of these

Solve by factoring: (2 x-3) (x-4) = (x-5)(x+3) + 7 The sum of the solutions is: A. ) 1 B. ) 9 C. ) -2 D. ) -9 F. ) None of these E. ) -1

Ms. Pain, the algebra teacher, has a habit of standing in front of crucial information. If she did the problem correctly (and she always does!), what is she blocking? Solve: x= 2 3 x = -1 2 6 x 2 =0 A. ) -x - 1 B. ) 2 x - 3 C. ) 3 x - 2 D. ) x + 1 E. ) -x - 2 F. ) None of these

Two of these quadratic equations share a common solution (i. e. one number is a solution to both equations). Find the two equations. I. ) x 2 = 24 - 5 x II. ) 2 x 2 + 2 x = 24 III. ) x 2+ 32 = 12 x Ice Cream is always a solution! A. ) I and II B. ) II and III C. ) I and III

Two of these quadratic equations share a common solution (i. e. one number is a solution to both equations). Find the two equations. I. ) 2 x 2 - 3 x = 35 II. ) 3 x 2+ 11 x - 20 = 0 III. ) 6 x 2 +29 x = - 28 A. ) I and II B. ) II and III C. ) I and III
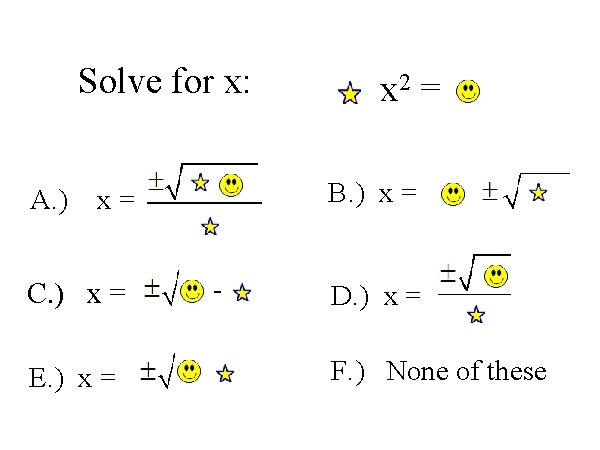
Solve for x: A. ) B. ) x = x= C. ) x = E. ) x = x 2 = - D. ) x = F. ) None of these
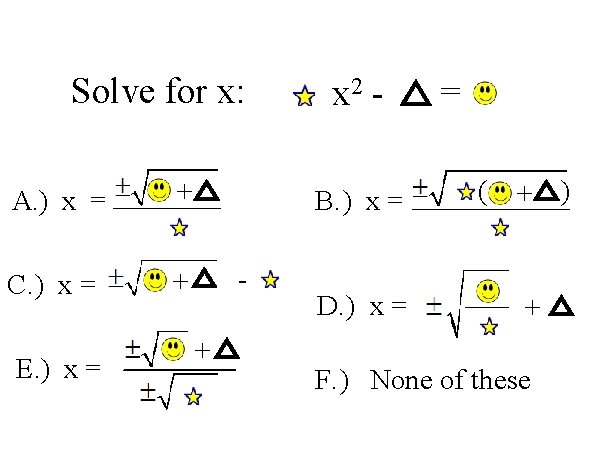
Solve for x: A. ) x = + C. ) x = + E. ) x = x 2 B. ) x = + D. ) x = = ( + ) + F. ) None of these

Ms. Pain, the algebra teacher, has a habit of standing in front of crucial information. If she did the problem correctly (and she always does!), what number is she blocking? x=1 x=4 A. ) 3/2 D. ) 9/4 B. ) 9/2 E. ) 7/2 5 2 (x- )2 = C. ) 3/4 F. ) None of these
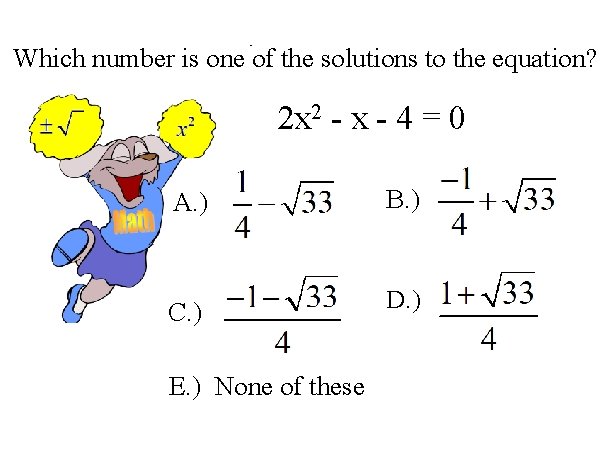
Which number is one of the solutions to the equation? 2 x 2 - x - 4 = 0 A. ) B. ) C. ) D. ) E. ) None of these

Which number is one of the solutions to the equation? 3 x 2 - 5 x - 1 = 0
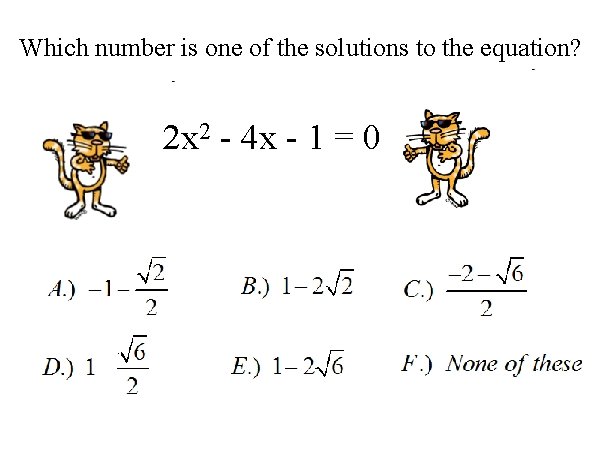
Which number is one of the solutions to the equation? 2 x 2 - 4 x - 1 = 0

Which number is one of the solutions to the equation? 7 x 2 - 8 x + 2 = 0

While solving a quadratic equation using the quadratic a = 2 b= -3 c = -5 formula, a study group spilled coffee on their paper. Which of the equations below could have been the original equation? A. ) 2(x 2 - x) = x + 5 B. ) (2 x+5)(x - 1) = 0 C. ) 2 x 2 - 1 = 3 x - 4 D. ) 2 x 2 - 5 x + 2 = 7 - 2 x E. ) 3 x - 5 = -2 x 2 F. ) None of these

Which statements are True? ? I. ) If x 2 = p and p ≥ 0, then x = II. ) If AB = 0, then A = 0 or B = 0 or both are = 0 III. ) If AB > 0, then either A > 0 and B > 0 or both > 0 A. ) I B. ) II C. ) III D. ) 1, II E. ) I, III F. ) II, III