Solving Quadratic Equations by Factoring Ways of finding

Solving Quadratic Equations by Factoring

Ways of finding the factors/ zeros 1. Quadratic formula 2. Factorization using zero property 3. By taking square roots 4. By squaring

Types of solutions 1. 2. 3. 4. Real roots Imaginary roots/ complex roots Fractions Decimals

Zero Product Property For any real numbers a and b, if ab=0, then either a=0, b=0, or both.

STEPS Solving a Quadratic Equation by Factoring Step 1 Write the equation in standard form. Step 2 Factor completely. Step 3 Use the zero-factor property. Set each factor with a variable equal to zero. Step 4 Solve each equation produced in step 3.

Quadratic Equations Standard Form

In this first example, the equation is already factored and is set equal to zero. To solve, simply set the individual factors equal to zero. The solutions are -3 and 1/2.

In this example, you must first factor the equation. Notice the familiar pattern. After factoring, set the individual factors equal to zero. Factor using “difference of two squares. ”

Now, try several problems. Write these on your own paper, showing all steps carefully.

Here are the answers. If all are correct, you’re finished!

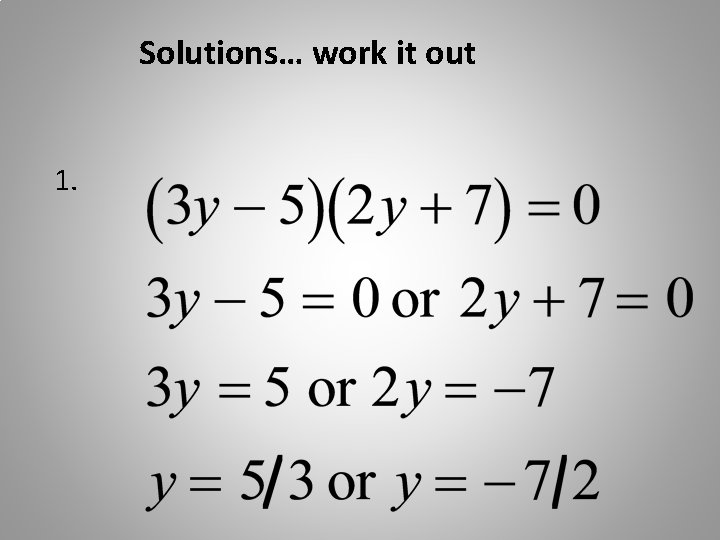
Solutions… work it out 1.

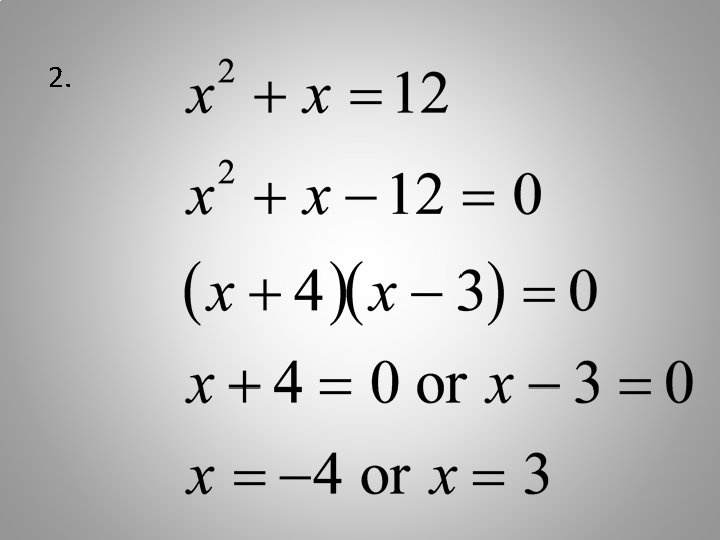
2.

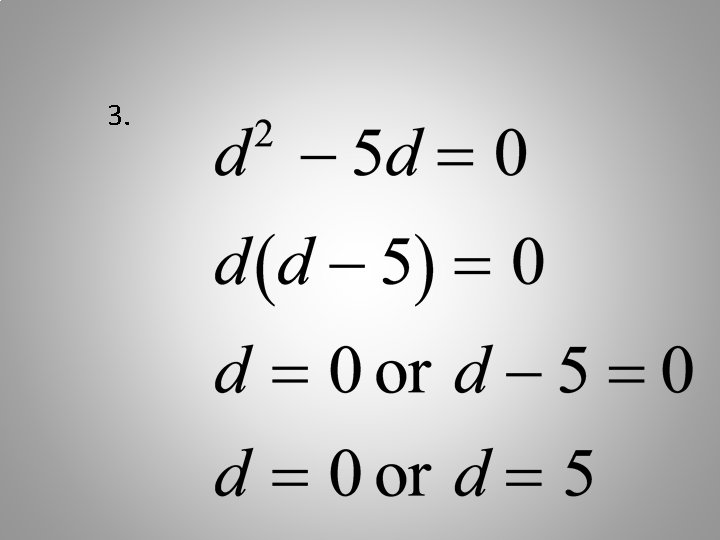
3.

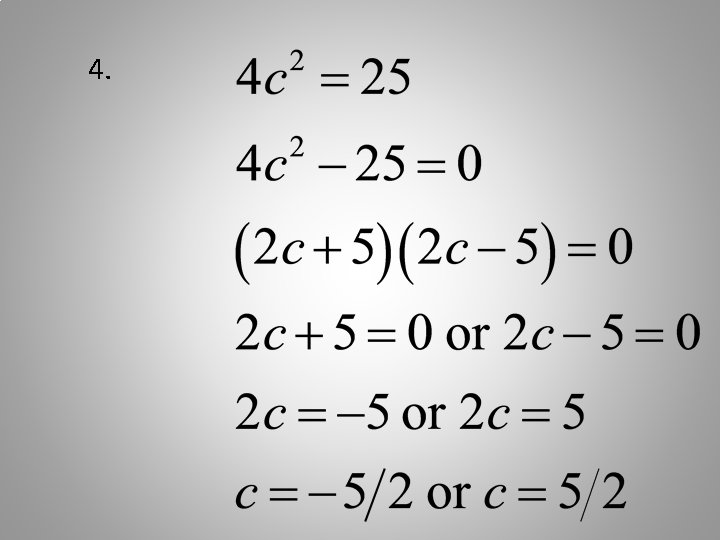
4.

How to factor a quadratic equation? Factoring a polynomial means expressing it as a product of other polynomials.

Factoring Method using difference of squares Factoring polynomials that are a difference of squares.

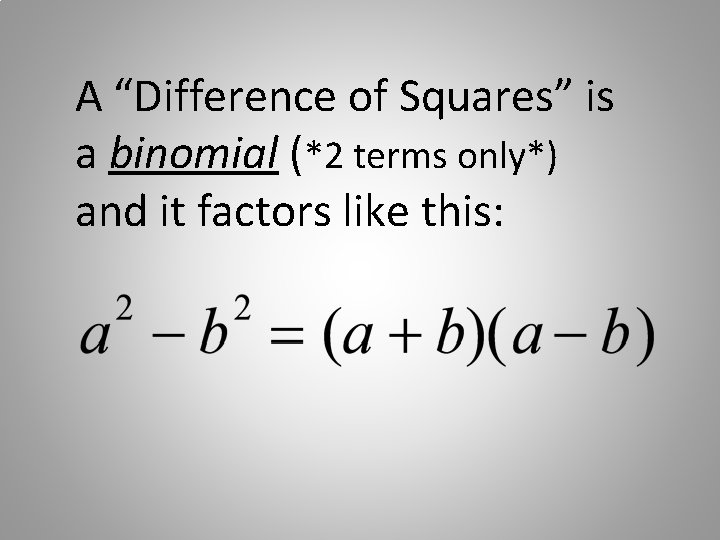
A “Difference of Squares” is a binomial (*2 terms only*) and it factors like this:

To factor, express each term as a square of a monomial then apply the rule. . .

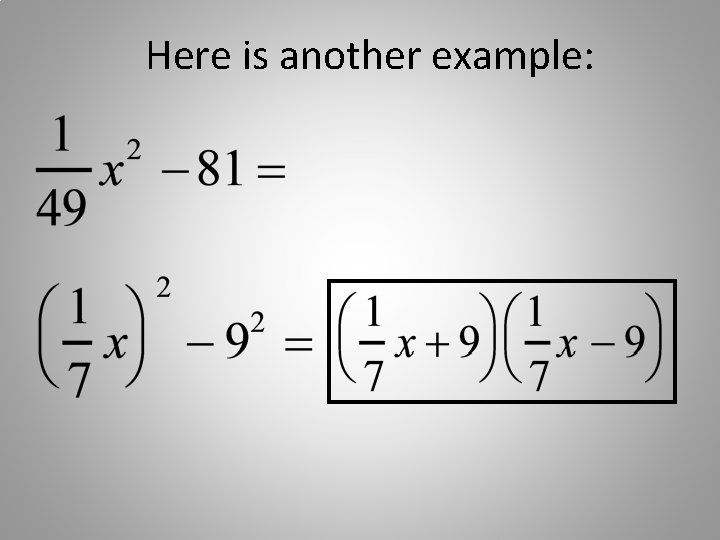
Here is another example:

Try these on your own:

Factoring Method Finding gcf Factoring polynomials with a common monomial factor (using GCF). **Always look for a GCF before using any other factoring method.

Steps: 1. Find the greatest common factor (GCF). 2. Divide the polynomial by the GCF. The quotient is the other factor. 3. Express the polynomial as the product of the quotient and the GCF.

This one uses a different technique than the previous ones. Really, this is something you should consider at the beginning of every factoring problem. See if you can solve it. Did you take out GCF?

Step 1: Step 2: Divide by GCF

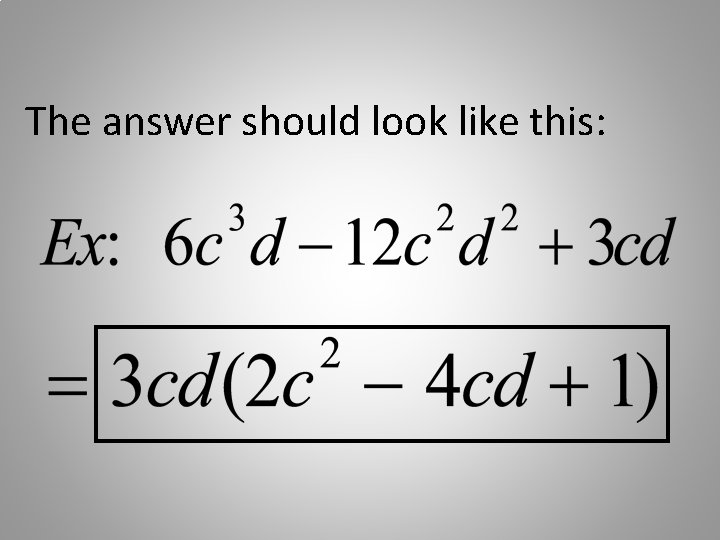
The answer should look like this:

Factor these on your own looking for a GCF.

Factoring Method Factoring a trinomial in the form:

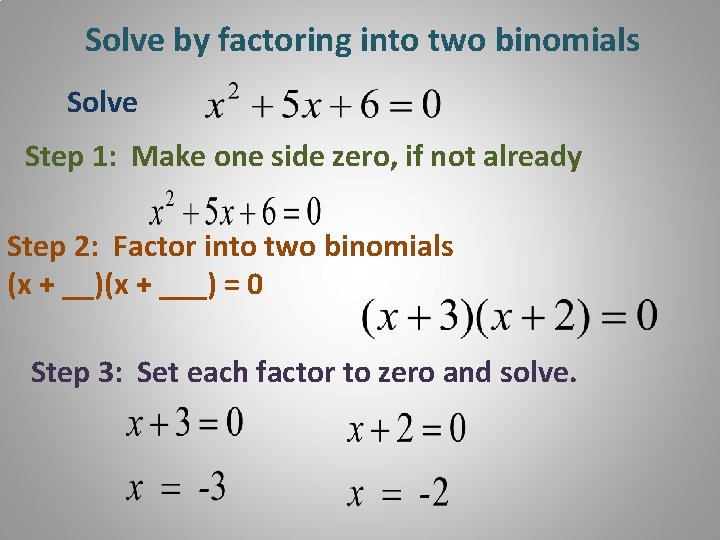
Solve by factoring into two binomials Solve Step 1: Make one side zero, if not already Step 2: Factor into two binomials (x + __)(x + ___) = 0 Step 3: Set each factor to zero and solve.

Factoring a trinomial: 1. Write two sets of parenthesis, ( )( ). These will be the factors of the trinomial. 2. Product of first terms of both binomials must equal first term of the trinomial. Next

Factoring a trinomial: 3. The product of last terms of both binomials must equal last term of the trinomial (c). 4. Think of the FOIL method of multiplying binomials, the sum of the outer and the inner products must equal the middle term (bx).

x x -2 -4 O + I = bx ? Factors of +8: 1&8 1 x + 8 x = 9 x 2&4 2 x + 4 x = 6 x -1 & -8 -1 x - 8 x = -9 x -2 & -4 -2 x - 4 x = -6 x

Check your answer by using FOIL F O I L

In the next example, you must set the equation equal to zero before factoring. Then set the individual factors equal to zero and solve.

Re-write this example in the proper form. Notice that the leading coefficient is not one. Use an appropriate factoring technique. Then solve as you have done before.

Practice Solve One side needs to be zero first!

Practice Solve Divide both sides by GCF first!

Factoring Technique continued Factoring a perfect square trinomial in the form:

Perfect Square Trinomials can be factored just like other trinomials (guess and check), but if you recognize the perfect squares pattern, follow the formula!

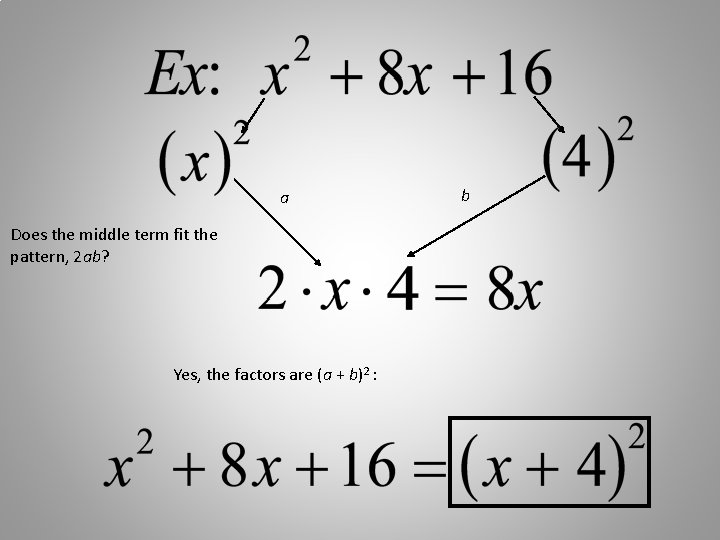
a Does the middle term fit the pattern, 2 ab? Yes, the factors are (a + b)2 : b

Practice Solve One side needs to be zero first!

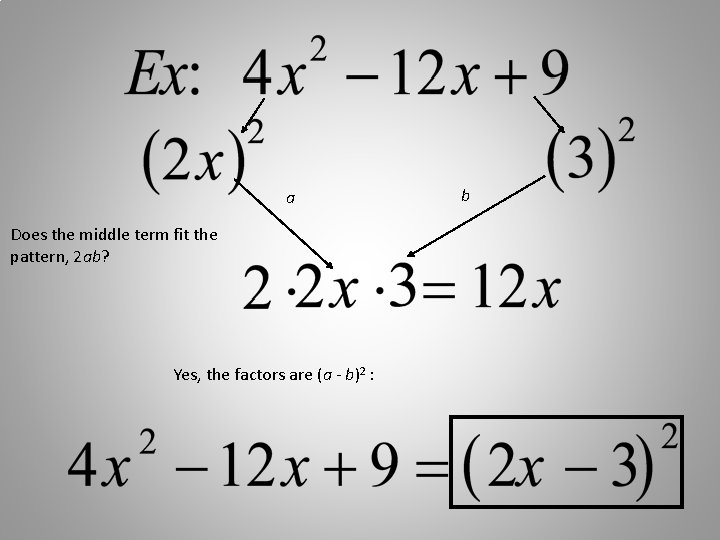
a Does the middle term fit the pattern, 2 ab? Yes, the factors are (a - b)2 : b

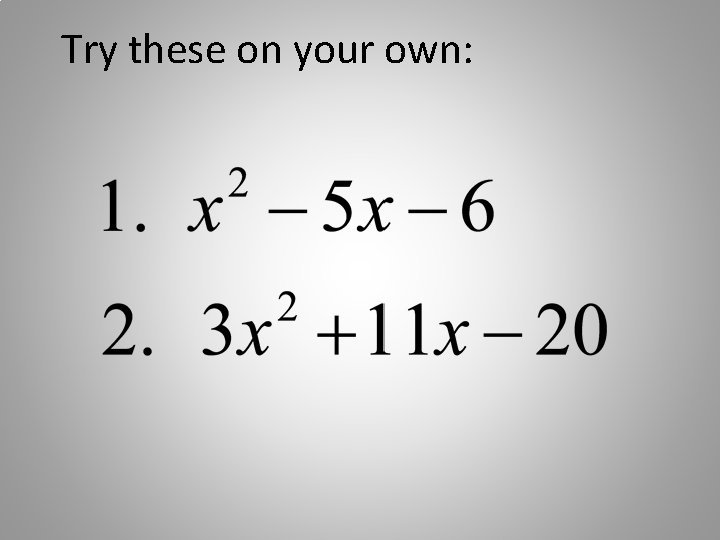
Try these on your own:

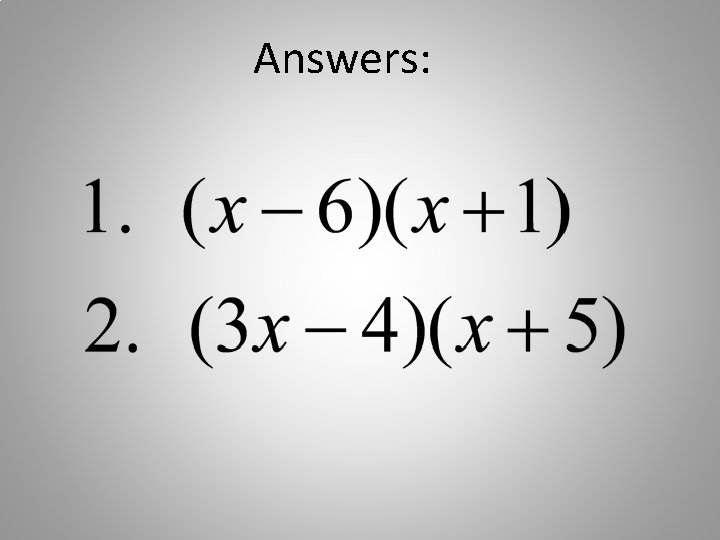
Answers:

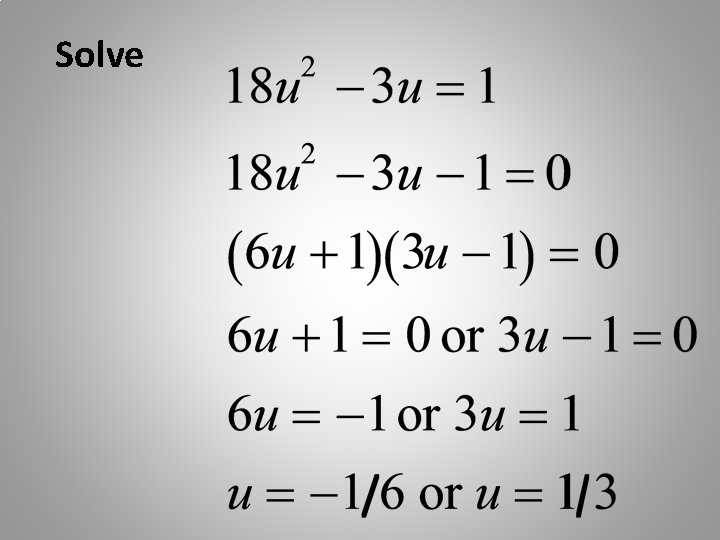
Solve

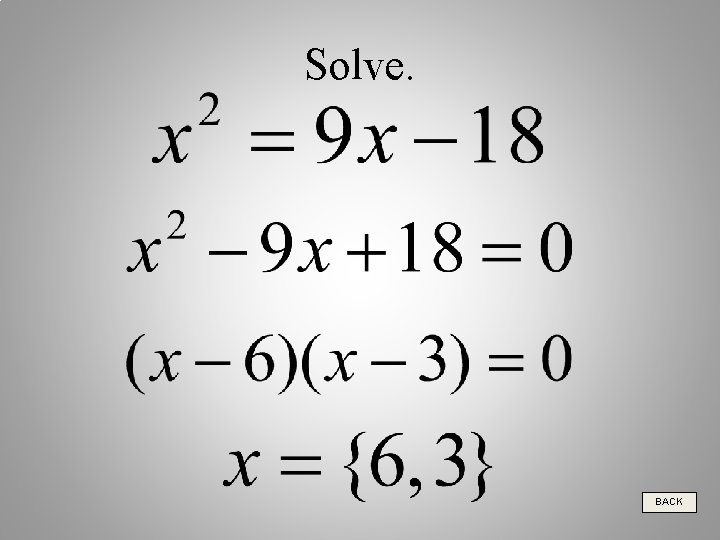
Solve. BACK

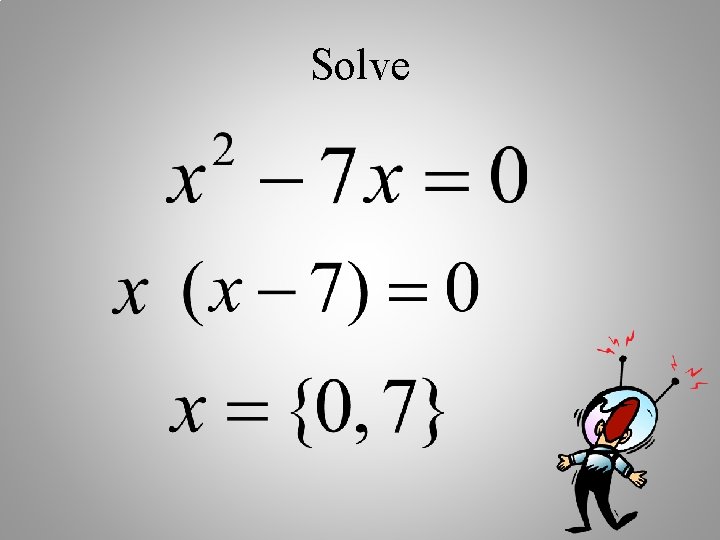
Solve

Number Of Solutions • The degree of a polynomial is equal to the number of solutions. Three solutions!!!

Solve the following equations. 1. x 2 – 25 = 0 2. x 2 + 7 x – 8 = 0 3. x 2 – 12 x + 36 = 0 4. c 2 – 8 c = 0

1. Get a value of zero on one side of the equation. 2. Factor the polynomial if possible. 3. Apply the zero product property by setting each factor equal to zero. 4. Solve for the variable.

SOLVING QUADRATIC EQUATIONS- When to use what? ? ? Get the equation in standard form: If there is no middle term (b = 0) then get the x 2 alone and square root both sides (if you get a negative under the square root there are no real solutions). If there is no constant term (c = 0) then factor out the common x and solve (set each factor = 0). If a, b and c are non-zero, see if you can factor and use the factor law to solve. If it doesn't factor or is hard to factor, use the quadratic formula to solve (if you get a negative under the square root there are no real solutions).

Vocabulary • If b 2 = a then b is a square root of a. • All positive real numbers have two square roots – A positive square root (or principle square root) and a negative square root. – This is written as

Vocabulary • A square root is written with the radical symbol • The number or expression inside the radical symbol is the radicand.

Vocabulary • The square of an integer is called a perfect square. Give some examples of perfect squares

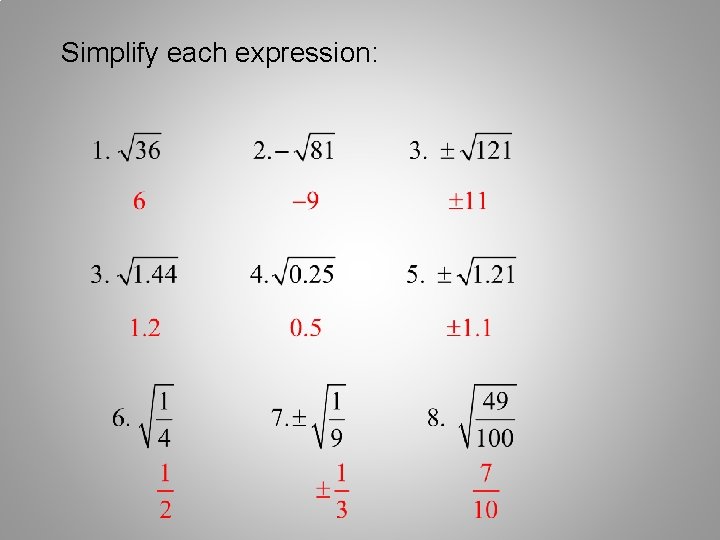
Simplify each expression:

Solving Quadratic Equations: 
 Solving by Taking Square Roots • Isolate the squared variable term • Put the number over on the other side

Solving quadratics by taking square roots • Solve each equation. a. x 2=4 b. x 2=5 c. x 2=0 d. x 2=-1 x 2=4 has two solutions, x = 2, x = -2 x 2=5 has two solutions, x =√ 5, x =- √ 5 x 2=0 has one solution, x = 0 x 2=-1 has no real solution

x 2 – 4 = 0 
x 2 = 4 I know that, when solving an equation, I can do whatever I like to that equation as long as I do the same thing to both sides of the equation. On the left -hand side of this particular equation, I have an x 2, and I need a plain x. To turn an x 2 into an x, I can take the square root of each side of the equation: 
x = ± 2 Then the solution is x = ± 2

Example 2: • Solve 9 m 2 = 169

Example 1: • Solve the equation: – x 2 – 7 = 9 – z 2 + 13 = 5

Solve x 2 – 50 = 0. This quadratic has a squared part and a number part. I'll start by adding the numerical term to the other side of the equaion (so the squared part is by itself), and then I'll square-root both sides. I'll need to remember to simplify the square root:

Solve by rewriting equation • Solve 3 x 2 – 48 = 0 3 x 2 – 48 + 48 = 0 + 48 3 x 2 = 48 3 x 2 / 3 = 48 / 3 x 2 = 16 After taking square root of both sides, x=± 4

Solving Quadratics by Using Square Roots Solve each equation. Ex. 5 Ex. 6 Ex. 7 ß Can’t take the square root of a negative.

Solving Quadratics by Using Square Roots Solve the following for x. Ex. 4 Add 98 to both sides. Divide both sides by 2. Square root both sides. Remember: When you square root something, it gives you a plus and a minus answer.

Example 3: • Solve 2 x 2 + 5 = 15

Example 4: • Solve 3(x + 3)2 = 39

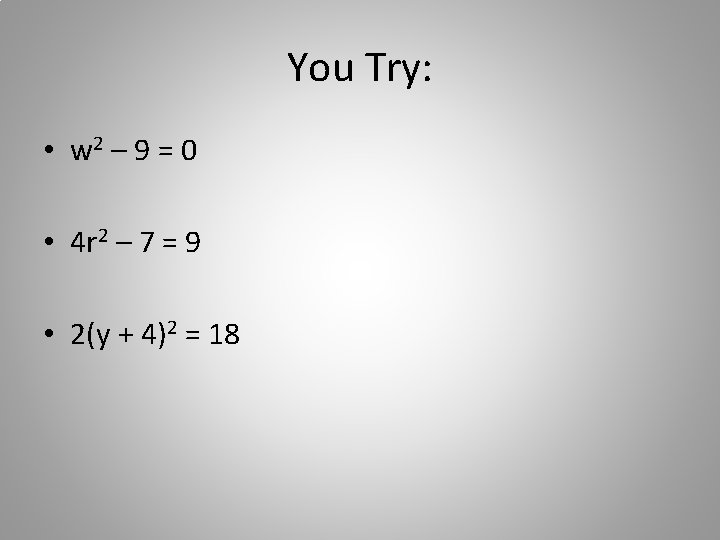
You Try: • w 2 – 9 = 0 • 4 r 2 – 7 = 9 • 2(y + 4)2 = 18

Equation of a falling object • When an object is dropped, the speed with which it falls continues to increase. Ignoring air resistance, its height h can be approximated by the falling object model. h is the height in feet above the ground t is the number of seconds the object has been falling s is the initial height from which the object was dropped

Application An engineering student is in an “egg dropping contest. ” The goal is to create a container for an egg so it can be dropped from a height of 32 feet without breaking the egg. To the nearest tenth of a second, about how long will it take for the egg’s container to hit the ground? Assume there is no air resistance.

• The question asks to find the time it takes for the container to hit the ground. • Initial height (s) = 32 feet • Height when its ground (h) = 0 feet • Time it takes to hit ground (t) = unknown

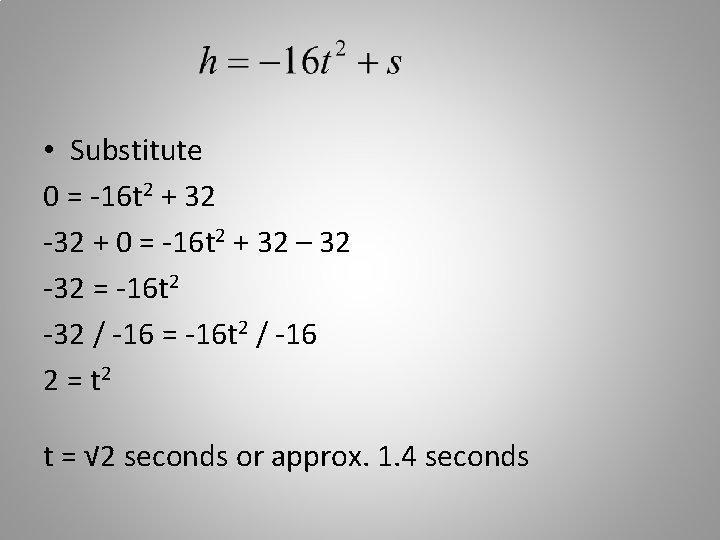
• Substitute 0 = -16 t 2 + 32 -32 + 0 = -16 t 2 + 32 – 32 -32 = -16 t 2 -32 / -16 = -16 t 2 / -16 2 = t 2 t = √ 2 seconds or approx. 1. 4 seconds

Solving Quadratic Equations by Completing the Square

Perfect Square Trinomials l l Examples x 2 + 6 x + 9 x 2 - 10 x + 25 x 2 + 12 x + 36

Creating a Perfect Square Trinomial l In the following perfect square trinomial, the constant term is missing. X 2 + 14 x + ____ Find the constant term by squaring half the coefficient of the linear term. (14/2)2 X 2 + 14 x + 49

Perfect Square Trinomials l l Create perfect square trinomials. x 2 + 20 x + ___ x 2 - 4 x + ___ x 2 + 5 x + ___ 100 4 25/4

Solving Quadratic Equations by Completing the Square Solve the following equation by completing the square: Step 1: Move quadratic term, and linear term to left side of the equation

Solving Quadratic Equations by Completing the Square Step 2: Find the term that completes the square on the left side of the equation. Add that term to both sides.

Solving Quadratic Equations by Completing the Square Step 3: Factor the perfect square trinomial on the left side of the equation. Simplify the right side of the equation.

Solving Quadratic Equations by Completing the Square Take the square root of each side Step 4:

Solving Quadratic Equations by Completing the Square Step 5: Set up the two possibilities and solve

Completing the Square-Example #2 Solve the following equation by completing the square: Step 1: Move quadratic term, and linear term to left side of the equation, the constant to the right side of the equation.

Solving Quadratic Equations by Completing the Square Step 2: Find the term that completes the square on the left side of the equation. Add that term to both sides. The quadratic coefficient must be equal to 1 before you complete the square, so you must divide all terms by the quadratic coefficient first.

Solving Quadratic Equations by Completing the Square Step 3: Factor the perfect square trinomial on the left side of the equation. Simplify the right side of the equation.

Solving Quadratic Equations by Completing the Square Step 4: Take the square root of each side

Ex 4 Solve by completing the square

Solving Quadratic Equations by Completing the Square: Try the following examples. Do your work on your paper and then check your answers.

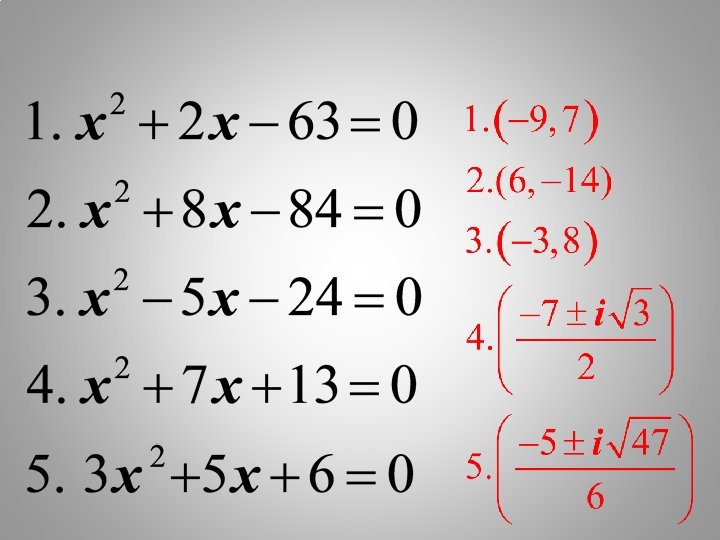
Solving Equations by graphing When we talk about solving these equations, we want to find the value of x when y = 0. These values, where the graph crosses the x-axis, are called the x-intercepts. These values are also referred to as solutions, zeros, or roots.

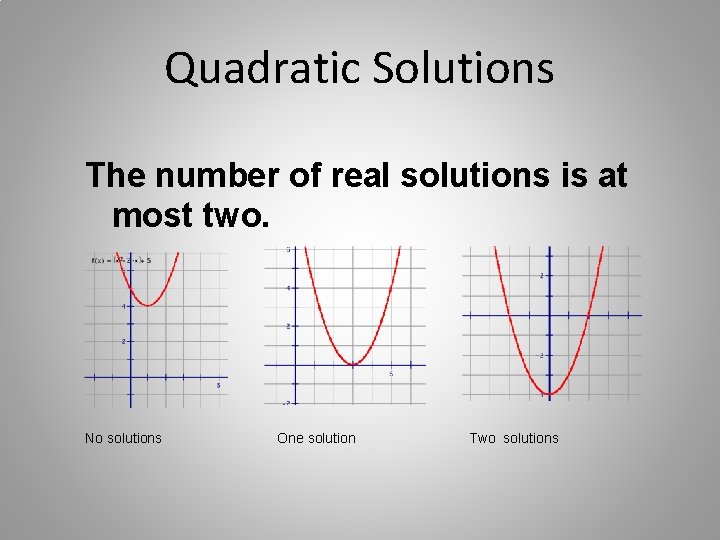
Quadratic Solutions The number of real solutions is at most two. No solutions One solution Two solutions

Graphing Quadratic Equations The graph of a quadratic equation is a parabola. The roots or zeros are the xintercepts. The vertex is the maximum or minimum point. All parabolas have an axis of symmetry.

Graph y= -x 2 - 2 x + 8 and find its roots. Vertex: (-1, 9) Roots: (-4, 0) (2, 0) Viewing window: Xmin= -10 Xmax=10 Ymin= -10 Ymax= 10

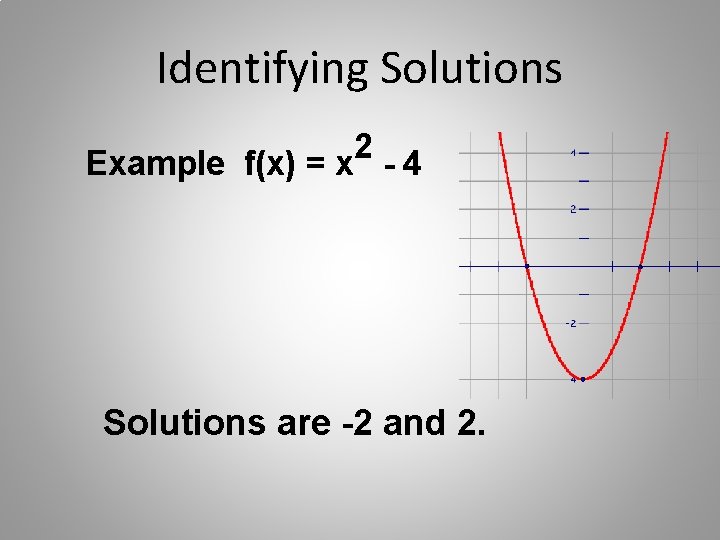
Identifying Solutions 2 Example f(x) = x - 4 Solutions are -2 and 2.

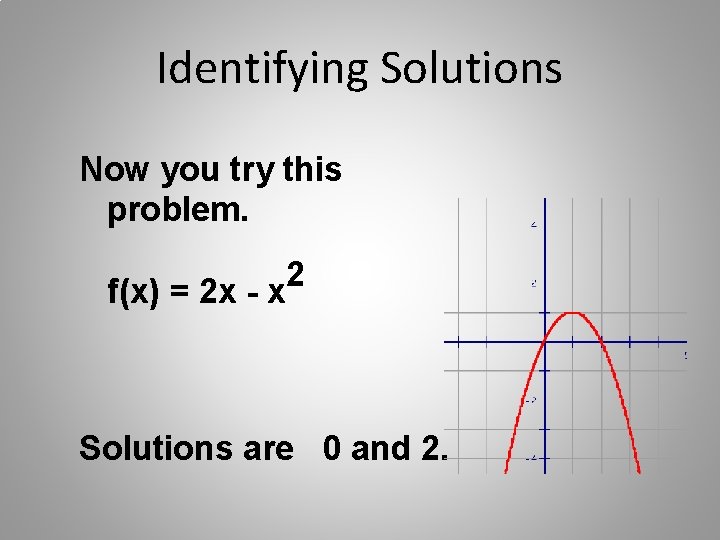
Identifying Solutions Now you try this problem. f(x) = 2 x - x 2 Solutions are 0 and 2.

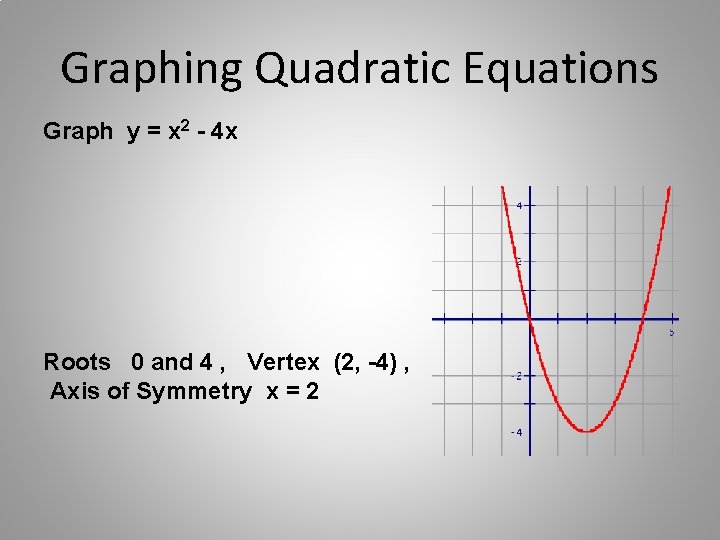
Graphing Quadratic Equations Graph y = x 2 - 4 x Roots 0 and 4 , Vertex (2, -4) , Axis of Symmetry x = 2

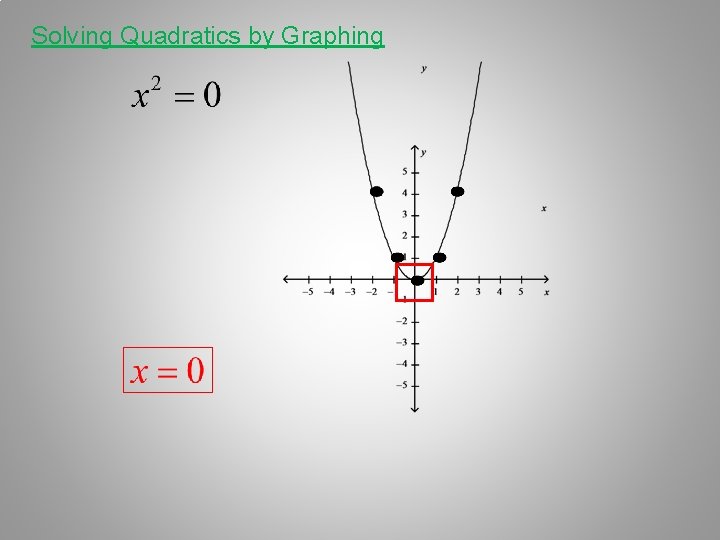
Solving Quadratics by Graphing

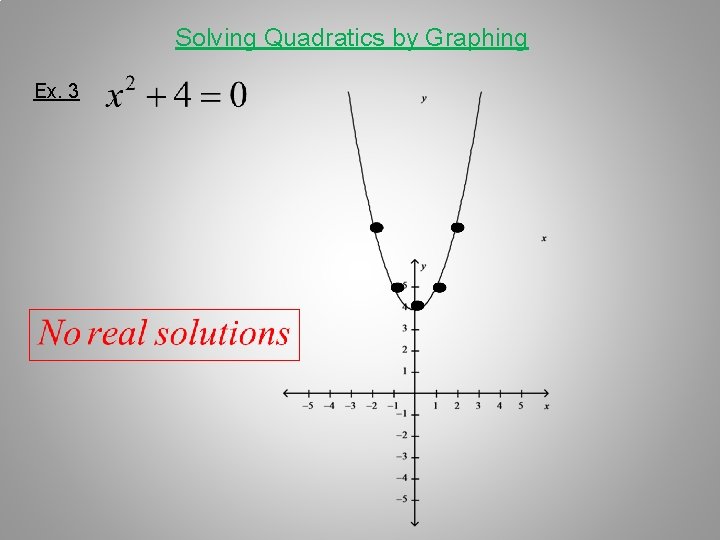
Solving Quadratics by Graphing Ex. 3

I can solve quadratic equations by graphing. I can solve quadratic equations by using square roots.