PRESSURE I am teaching Engineering Thermodynamics to a










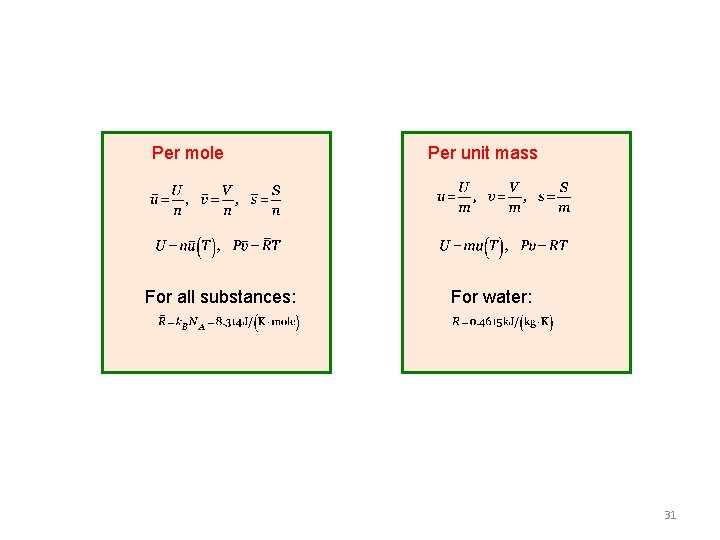





















- Slides: 67

PRESSURE • I am teaching Engineering Thermodynamics to a class of 75 undergraduate students. • These slides follow closely my written notes (http: //imechanica. org/node/288). • I went through these slides in three 90 -minute lectures. Zhigang Suo, Harvard University

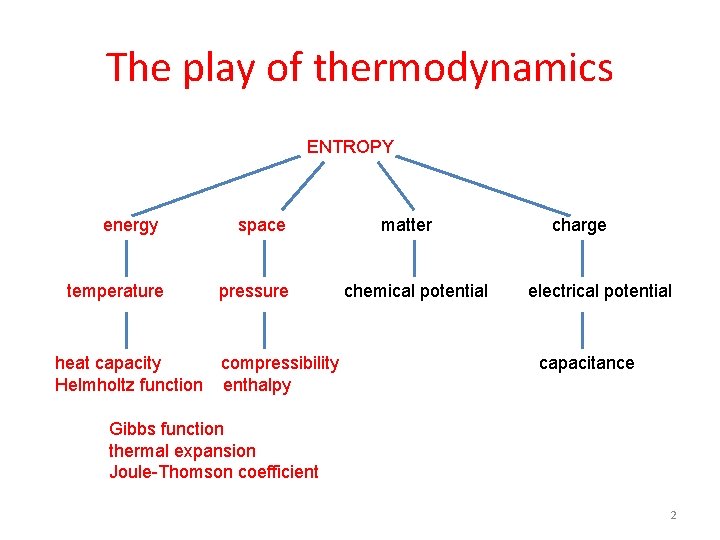
The play of thermodynamics ENTROPY energy temperature heat capacity Helmholtz function space pressure compressibility enthalpy matter chemical potential charge electrical potential capacitance Gibbs function thermal expansion Joule-Thomson coefficient 2

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 3

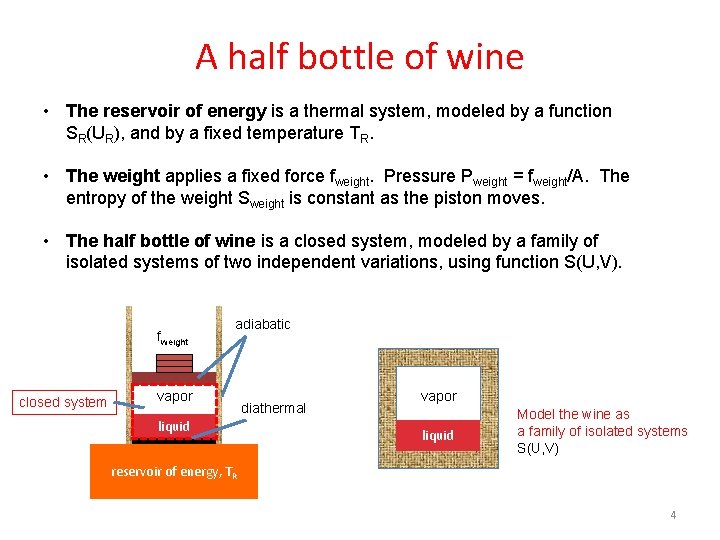
A half bottle of wine • The reservoir of energy is a thermal system, modeled by a function SR(UR), and by a fixed temperature TR. • The weight applies a fixed force fweight. Pressure Pweight = fweight/A. The entropy of the weight Sweight is constant as the piston moves. • The half bottle of wine is a closed system, modeled by a family of isolated systems of two independent variations, using function S(U, V). fweight closed system adiabatic vapor liquid diathermal O vapor 2 liquid Model the wine as a family of isolated systems S(U, V) reservoir of energy, TR 4

The basic algorithm of thermodynamics Entropy = log (number of quantum states). Entropy is additive. 1. Construct an isolated system with an internal variable, x. 2. When the internal variable is constrained at x, the isolated system has entropy S(x). 3. After the constraint is lifted, x changes to maximize S(x). 5

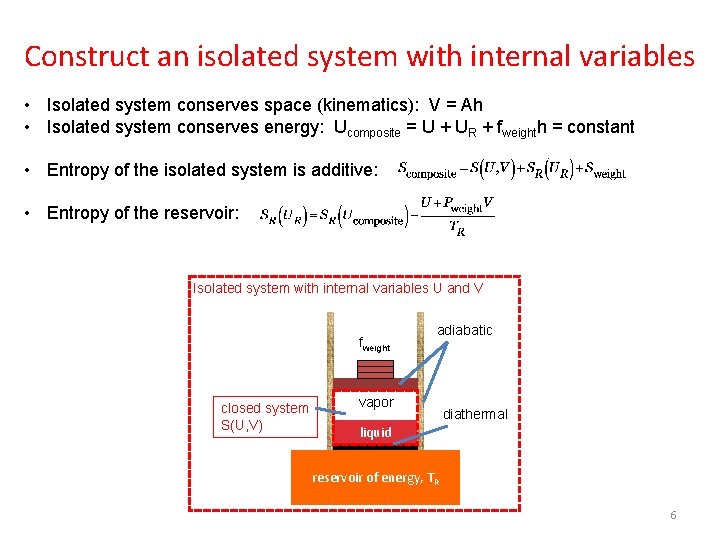
Construct an isolated system with internal variables • Isolated system conserves space (kinematics): V = Ah • Isolated system conserves energy: Ucomposite = U + UR + fweighth = constant • Entropy of the isolated system is additive: • Entropy of the reservoir: Isolated system with internal variables U and V fweight closed system S(U, V) adiabatic vapor diathermal liquid reservoir of energy, TR 6

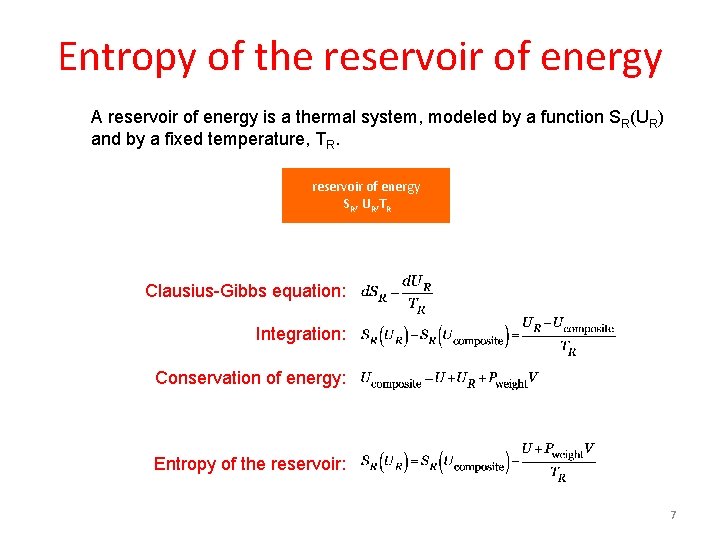
Entropy of the reservoir of energy A reservoir of energy is a thermal system, modeled by a function SR(UR) and by a fixed temperature, TR. reservoir of energy SR, UR, TR Clausius-Gibbs equation: Integration: Conservation of energy: Entropy of the reservoir: 7

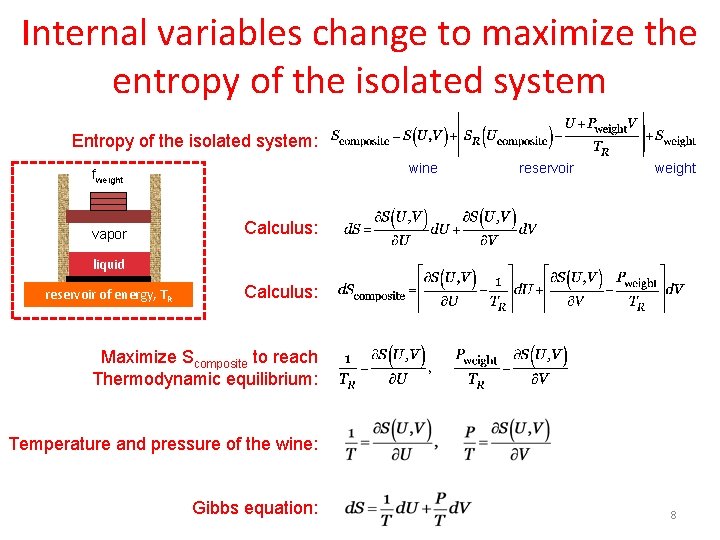
Internal variables change to maximize the entropy of the isolated system Entropy of the isolated system: wine fweight vapor reservoir weight Calculus: liquid reservoir of energy, TR Calculus: Maximize Scomposite to reach Thermodynamic equilibrium: Temperature and pressure of the wine: Gibbs equation: 8

Count the number of quantum states of a half bottle of wine Experimental determination of S(U, V) O vapor 2 liquid • • A family of isolated systems Five properties: U, V, S, P, T Two independent variables, U, V Measure V by geometry Measure U by calorimetry (e. g. , pass an electric current through a resistor) Measure T by thermometry Measure P by force/area • Obtain S by integrating the Gibbs equation 9

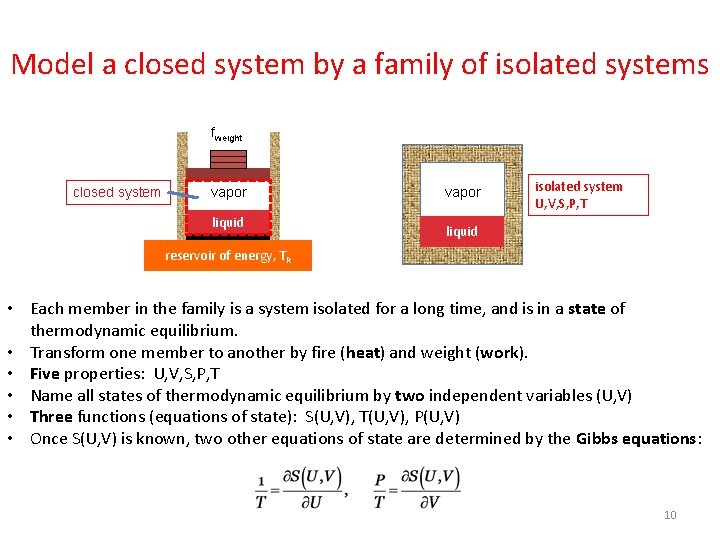
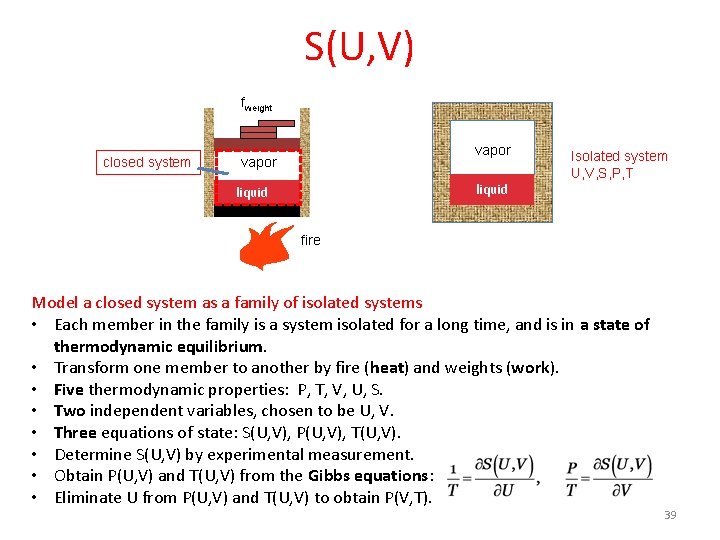
Model a closed system by a family of isolated systems fweight closed system vapor liquid O vapor 2 isolated system U, V, S, P, T liquid reservoir of energy, TR • Each member in the family is a system isolated for a long time, and is in a state of thermodynamic equilibrium. • Transform one member to another by fire (heat) and weight (work). • Five properties: U, V, S, P, T • Name all states of thermodynamic equilibrium by two independent variables (U, V) • Three functions (equations of state): S(U, V), T(U, V), P(U, V) • Once S(U, V) is known, two other equations of state are determined by the Gibbs equations: 10

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 11

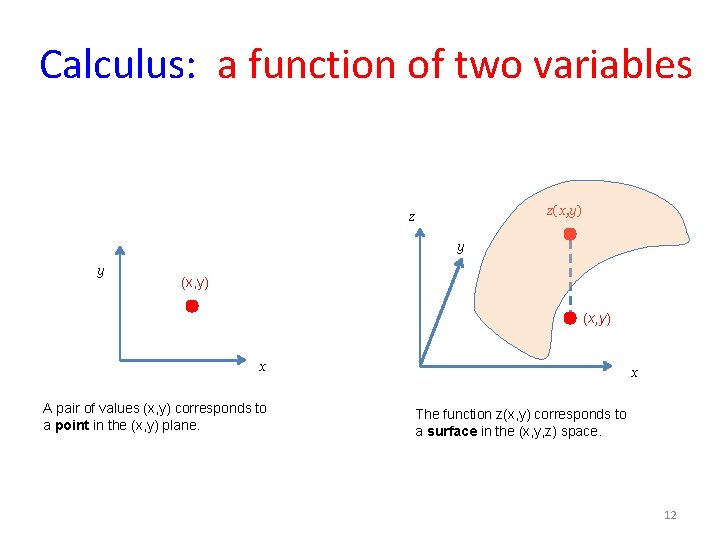
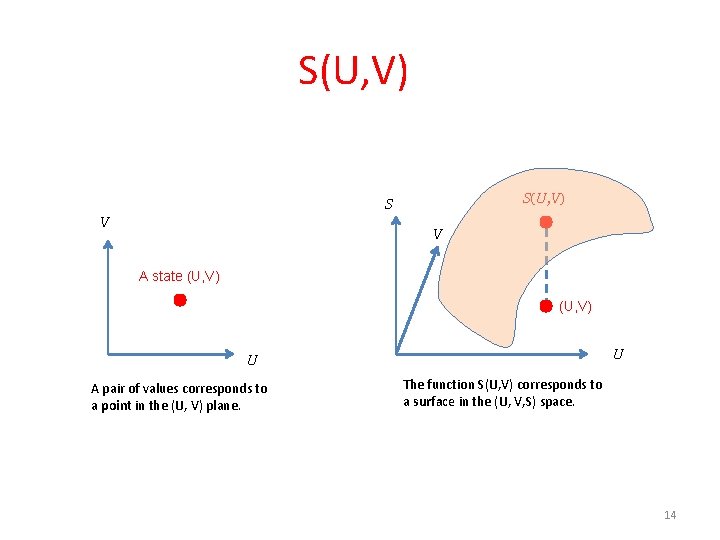
Calculus: a function of two variables z(x, y) z y y (x, y) x A pair of values (x, y) corresponds to a point in the (x, y) plane. x The function z(x, y) corresponds to a surface in the (x, y, z) space. 12

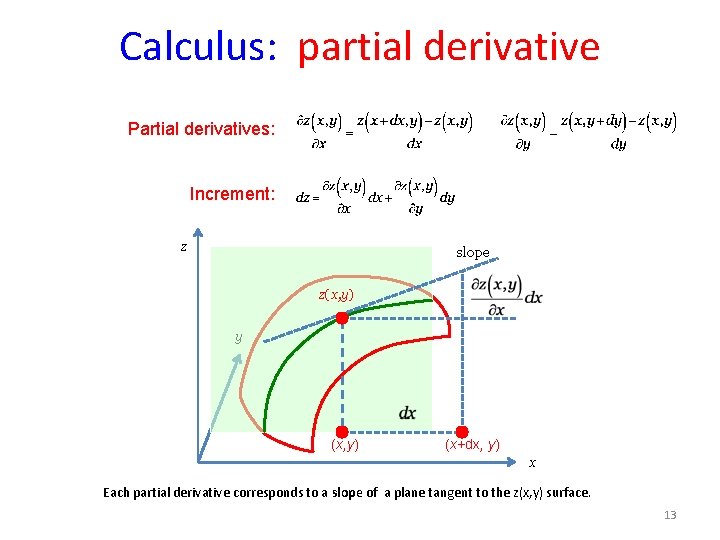
Calculus: partial derivative Partial derivatives: Increment: z slope z(x, y) y (x, y) (x+dx, y) x Each partial derivative corresponds to a slope of a plane tangent to the z(x, y) surface. 13

S(U, V) S V V A state (U, V) U U A pair of values corresponds to a point in the (U, V) plane. The function S(U, V) corresponds to a surface in the (U, V, S) space. 14

T(U, V) and P(U, V) • Given a state (U, V), draw a plane tangent to the surface S(U, V) • The two slopes of the tangent plane give T(U, V) and P(U, V). S V (P, T) (U, V) U 15

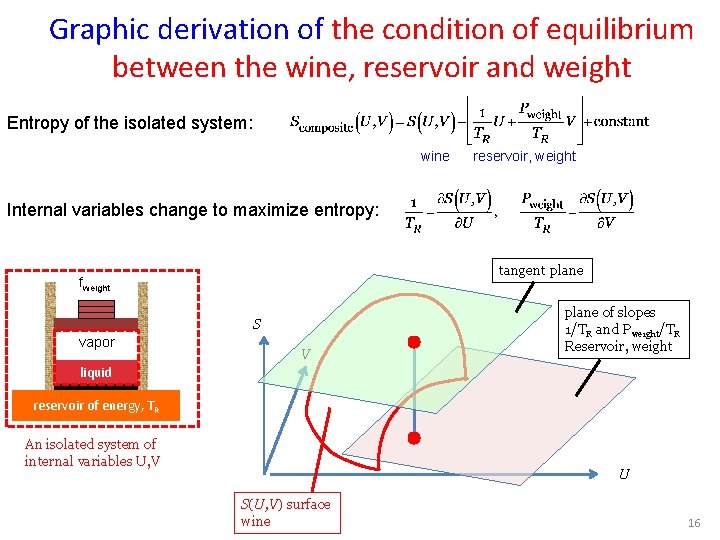
Graphic derivation of the condition of equilibrium between the wine, reservoir and weight Entropy of the isolated system: wine reservoir, weight Internal variables change to maximize entropy: tangent plane fweight S vapor V plane of slopes 1/TR and Pweight/TR Reservoir, weight liquid reservoir of energy, TR An isolated system of internal variables U, V U S(U, V) surface wine 16

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 17

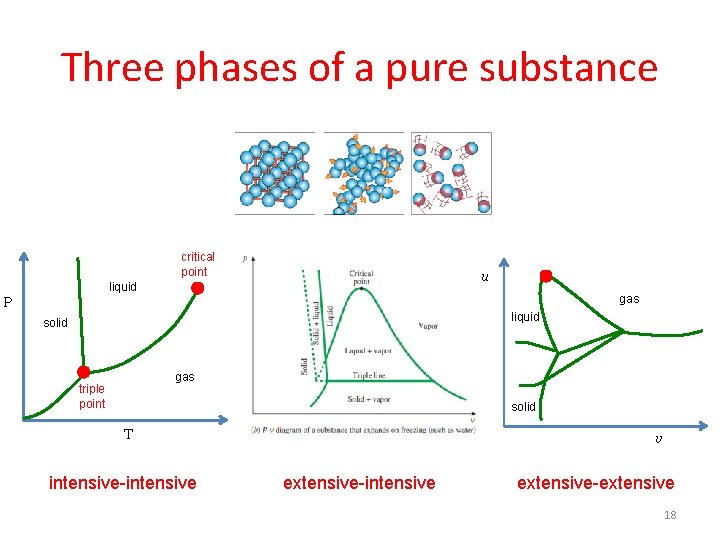
Three phases of a pure substance critical point u liquid gas P liquid solid gas triple point solid T intensive-intensive v extensive-intensive extensive-extensive 18

Calculus: convex function A function of two variables: Partial derivatives: Equivalent statements • z(x, y) is convex • Each tangent plane touches the surface at a single point. • Roll the tangent plane with two degrees of freedom • One-to-one correspondence: (M, N) (x, y). z y tangent plane of slopes M and N z(x, y) x 19

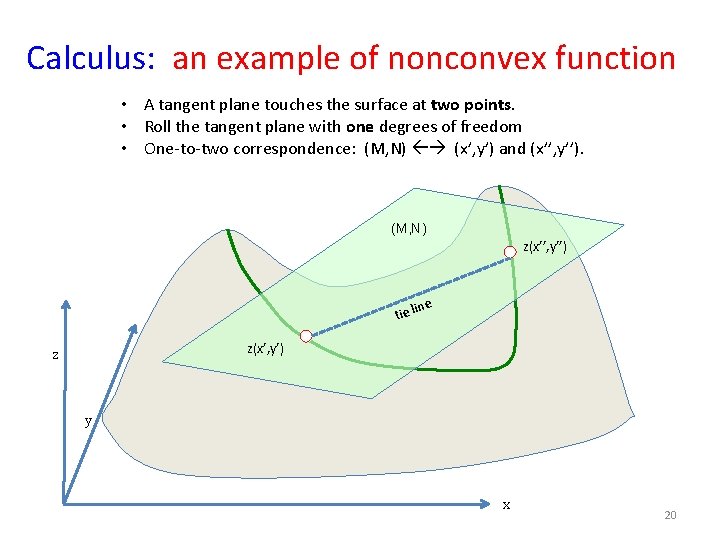
Calculus: an example of nonconvex function • A tangent plane touches the surface at two points. • Roll the tangent plane with one degrees of freedom • One-to-two correspondence: (M, N) (x’, y’) and (x’’, y’’). (M, N) z(x’’, y’’) ine tie l z(x’, y’) z y x 20

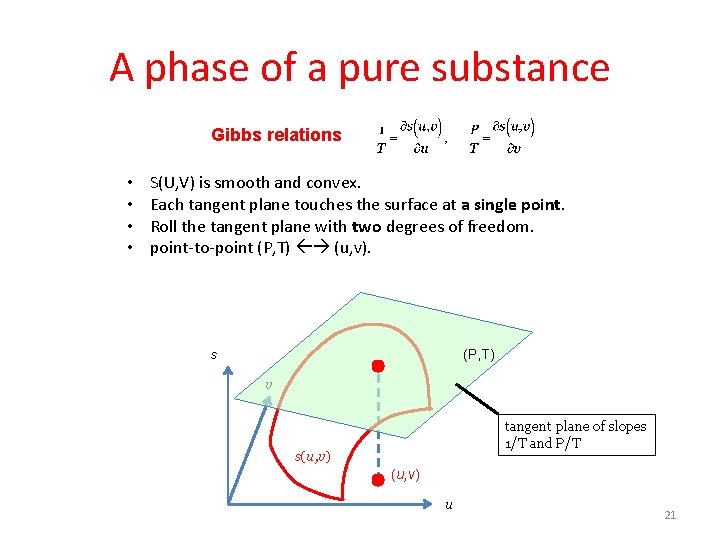
A phase of a pure substance Gibbs relations • • S(U, V) is smooth and convex. Each tangent plane touches the surface at a single point. Roll the tangent plane with two degrees of freedom. point-to-point (P, T) (u, v). s (P, T) v tangent plane of slopes 1/T and P/T s(u, v) u 21

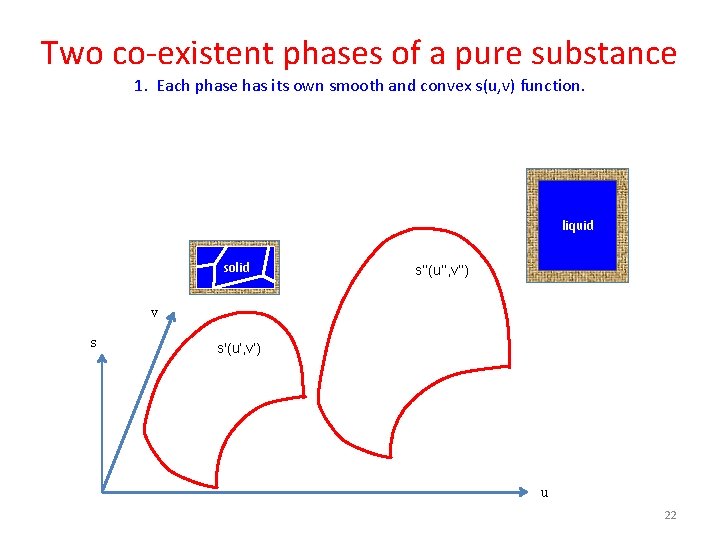
Two co-existent phases of a pure substance 1. Each phase has its own smooth and convex s(u, v) function. liquid solid s’’(u’’, v’’) v s s'(u’, v’) u 22

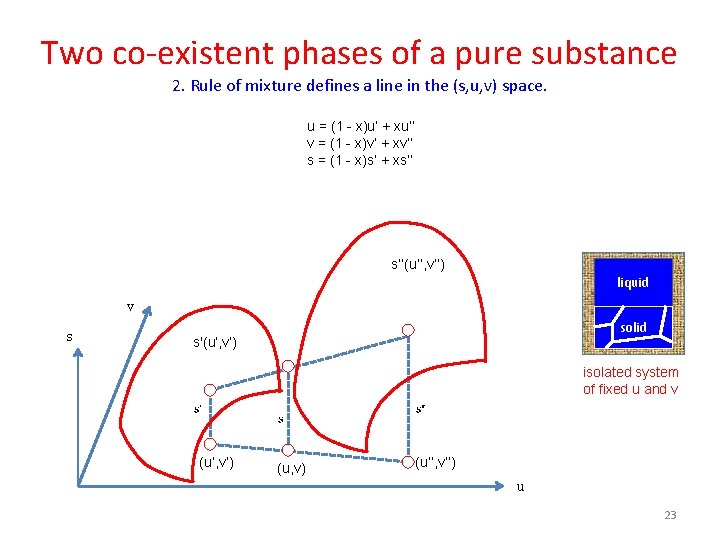
Two co-existent phases of a pure substance 2. Rule of mixture defines a line in the (s, u, v) space. u = (1 - x)u’ + xu’’ v = (1 - x)v’ + xv’’ s = (1 - x)s’ + xs’’ s’’(u’’, v’’) liquid v s solid s'(u’, v’) isolated system of fixed u and v (u’, v’) (u, v) (u’’, v’’) u 23

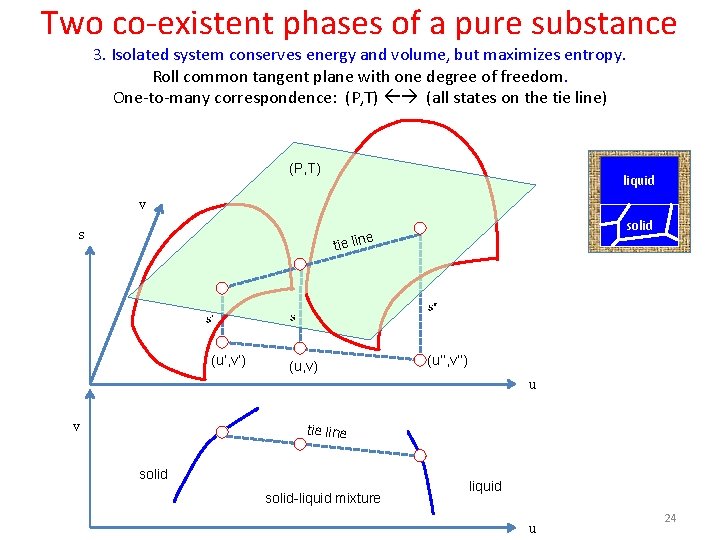
Two co-existent phases of a pure substance 3. Isolated system conserves energy and volume, but maximizes entropy. Roll common tangent plane with one degree of freedom. One-to-many correspondence: (P, T) (all states on the tie line) (P, T) liquid v s solid e line ti (u’, v’) (u, v) (u’’, v’’) u v tie line solid-liquid mixture liquid u 24

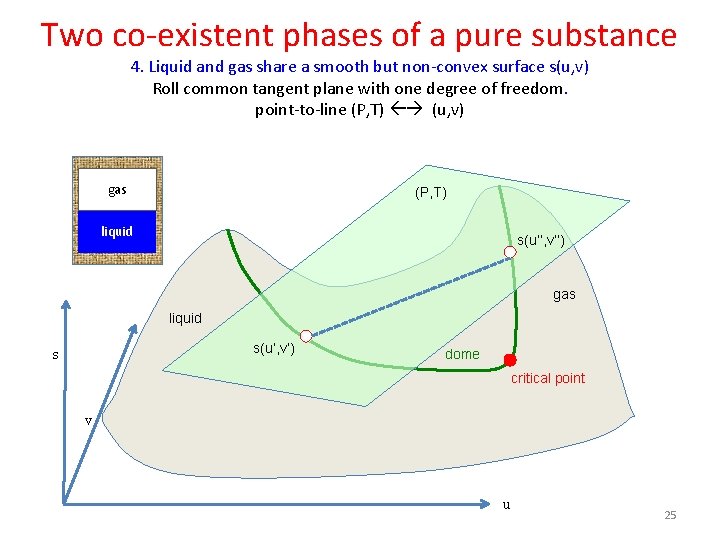
Two co-existent phases of a pure substance 4. Liquid and gas share a smooth but non-convex surface s(u, v) Roll common tangent plane with one degree of freedom. point-to-line (P, T) (u, v) gas (P, T) liquid s(u’’, v’’) gas liquid s(u’, v’) s dome critical point v u 25

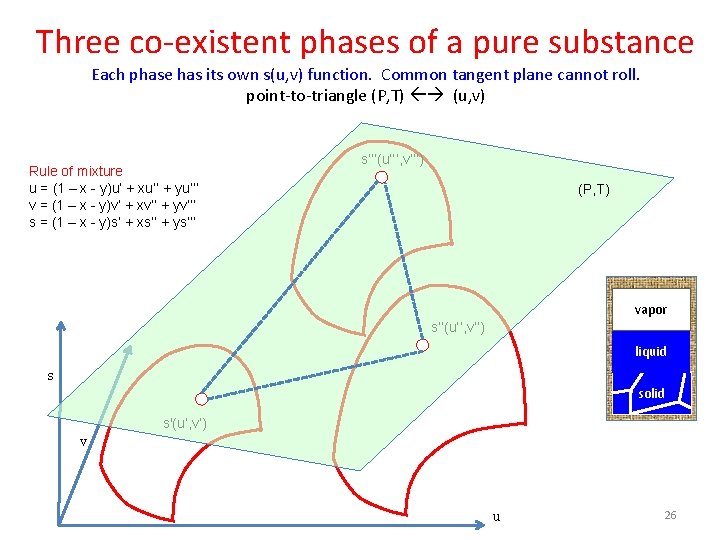
Three co-existent phases of a pure substance Each phase has its own s(u, v) function. Common tangent plane cannot roll. point-to-triangle (P, T) (u, v) Rule of mixture u = (1 – x - y)u’ + xu’’ + yu’’’ v = (1 – x - y)v’ + xv’’ + yv’’’ s = (1 – x - y)s’ + xs’’ + ys’’’(u’’’, v’’’) (P, T) vapor s’’(u’’, v’’) liquid s solid s'(u’, v’) v u 26

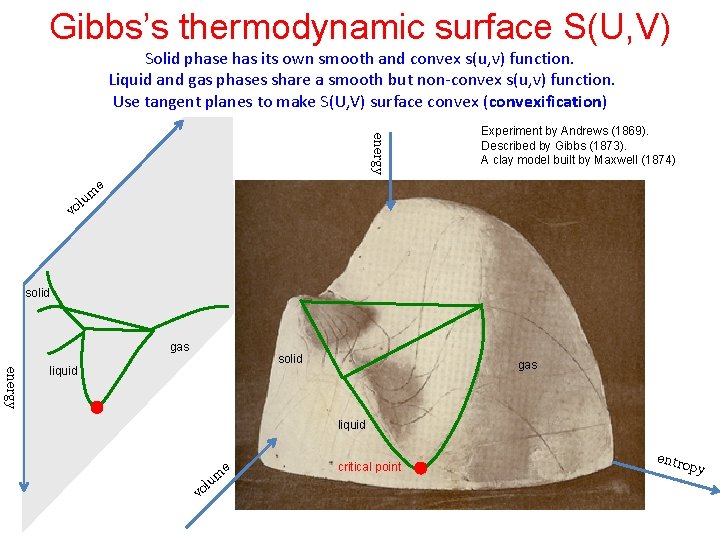
Gibbs’s thermodynamic surface S(U, V) Solid phase has its own smooth and convex s(u, v) function. Liquid and gas phases share a smooth but non-convex s(u, v) function. Use tangent planes to make S(U, V) surface convex (convexification) energy Experiment by Andrews (1869). Described by Gibbs (1873). A clay model built by Maxwell (1874) e um l vo solid gas solid energy liquid gas liquid e vo l um critical point entro py

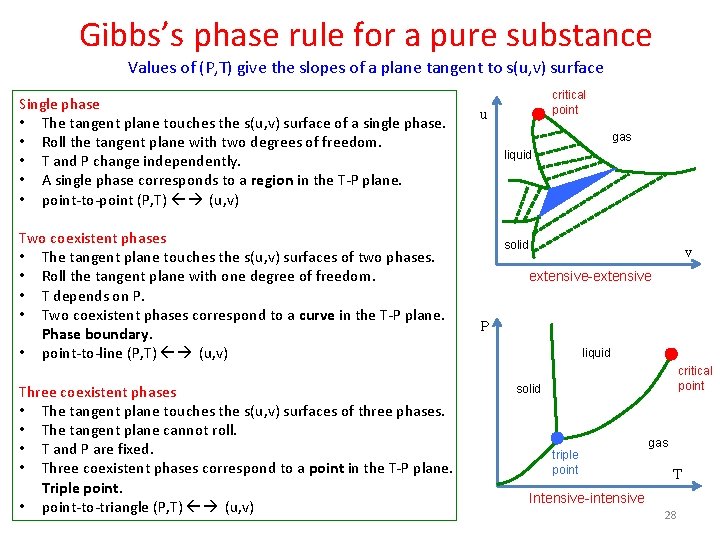
Gibbs’s phase rule for a pure substance Values of (P, T) give the slopes of a plane tangent to s(u, v) surface Single phase • The tangent plane touches the s(u, v) surface of a single phase. • Roll the tangent plane with two degrees of freedom. • T and P change independently. • A single phase corresponds to a region in the T-P plane. • point-to-point (P, T) (u, v) Two coexistent phases • The tangent plane touches the s(u, v) surfaces of two phases. • Roll the tangent plane with one degree of freedom. • T depends on P. • Two coexistent phases correspond to a curve in the T-P plane. Phase boundary. • point-to-line (P, T) (u, v) Three coexistent phases • The tangent plane touches the s(u, v) surfaces of three phases. • The tangent plane cannot roll. • T and P are fixed. • Three coexistent phases correspond to a point in the T-P plane. Triple point. • point-to-triangle (P, T) (u, v) critical point u gas liquid solid v extensive-extensive P liquid critical point solid triple point gas T Intensive-intensive 28

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 29

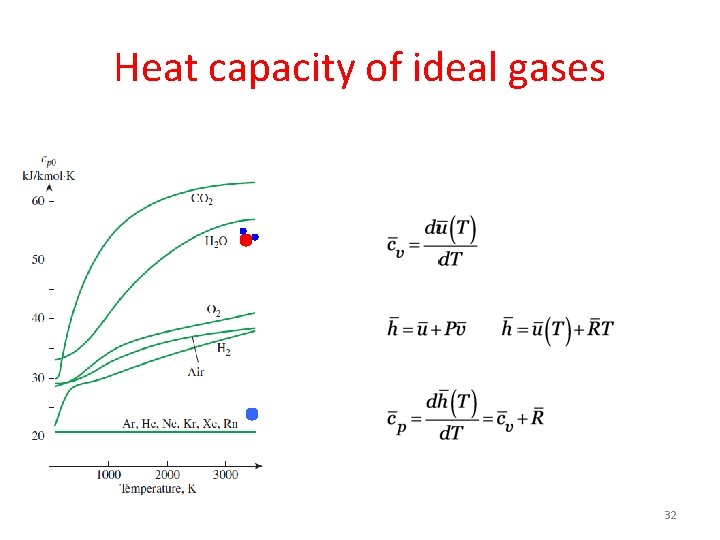
Ideal gas U, V, S, P, T, N, W When molecules are far apart, the probability of finding a molecule is independent of the location in the container, and of the presence of other molecules. Number of quantum states of the gas scales with VN Definition of entropy S = k. Blog W Gibbs equations: Equations of state for ideal gases: 30
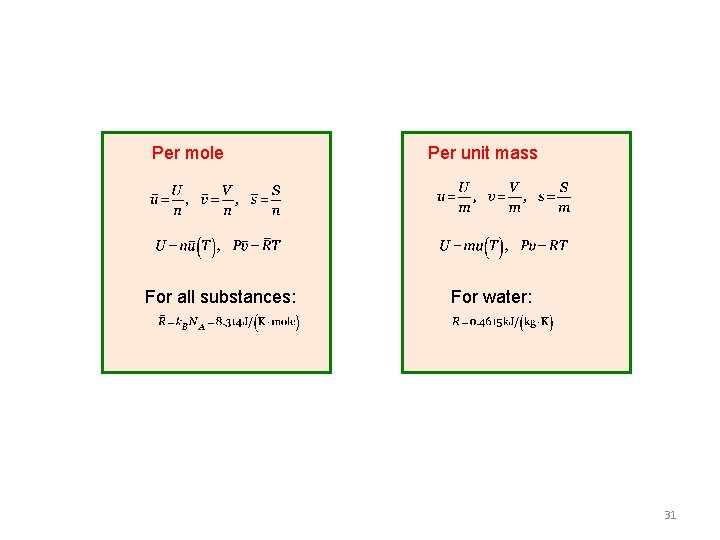
Per mole For all substances: Per unit mass For water: 31

Heat capacity of ideal gases 32

Entropy of ideal gas Gibbs equation: Laws of ideal gases: Increment for ideal gas: Approximation of constant specific heat isentropic process: 33

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 34

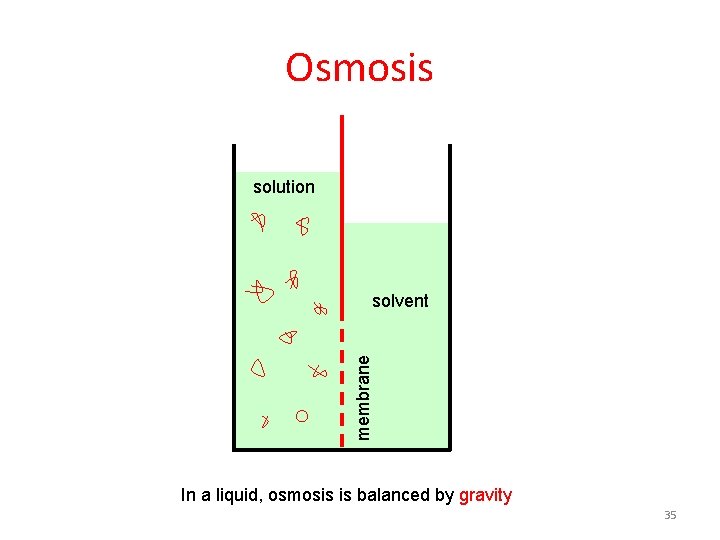
Osmosis solution membrane solvent In a liquid, osmosis is balanced by gravity 35

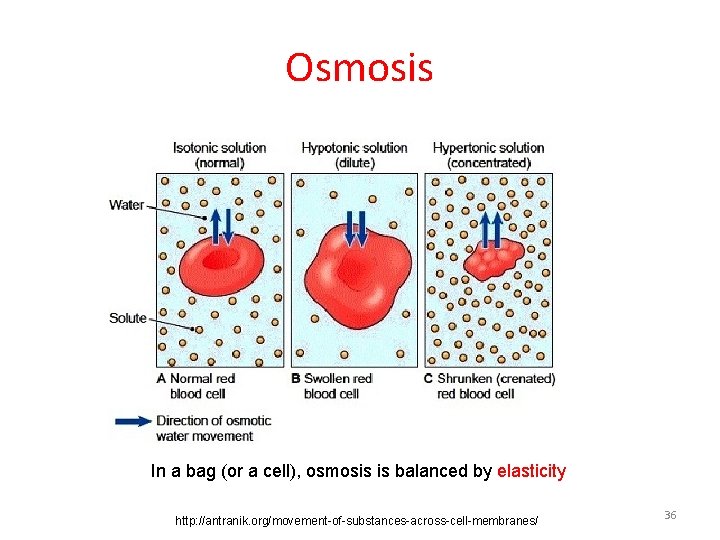
Osmosis In a bag (or a cell), osmosis is balanced by elasticity http: //antranik. org/movement-of-substances-across-cell-membranes/ 36

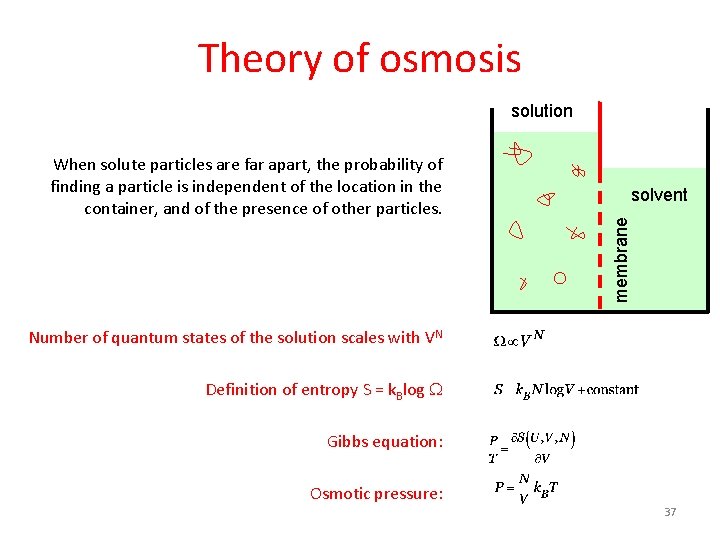
Theory of osmosis solution solvent membrane When solute particles are far apart, the probability of finding a particle is independent of the location in the container, and of the presence of other particles. Number of quantum states of the solution scales with VN Definition of entropy S = k. Blog W Gibbs equation: Osmotic pressure: 37

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 38

S(U, V) fweight closed system O vapor 2 vapor liquid Isolated system U, V, S, P, T fire Model a closed system as a family of isolated systems • Each member in the family is a system isolated for a long time, and is in a state of thermodynamic equilibrium. • Transform one member to another by fire (heat) and weights (work). • Five thermodynamic properties: P, T, V, U, S. • Two independent variables, chosen to be U, V. • Three equations of state: S(U, V), P(U, V), T(U, V). • Determine S(U, V) by experimental measurement. • Obtain P(U, V) and T(U, V) from the Gibbs equations: • Eliminate U from P(U, V) and T(U, V) to obtain P(V, T). 39

Calculus: Notation Function: Partial derivative: Name partial derivatives: Derivatives are functions: 40

U(S, V) When V is fixed, S increases with U. Invert S(U, V) to obtain U(S, V). S S(U, V) U(S, V) V(U, S) V U Gibbs equation: Another Gibbs equation Calculus: More Gibbs equations 41

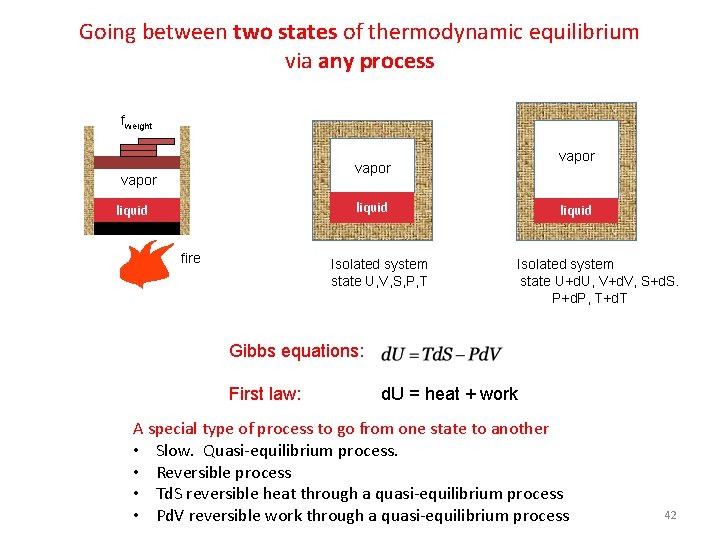
Going between two states of thermodynamic equilibrium via any process fweight 2 O O vapor liquid vapor 2 vapor liquid fire Isolated system state U, V, S, P, T Isolated system state U+d. U, V+d. V, S+d. S. P+d. P, T+d. T Gibbs equations: First law: d. U = heat + work A special type of process to go from one state to another • Slow. Quasi-equilibrium process. • Reversible process • Td. S reversible heat through a quasi-equilibrium process • Pd. V reversible work through a quasi-equilibrium process 42

Calculus: Legendre transform Turn a derivative into an independent variable A function of two variables: Partial derivatives: Increment: Define a Legendre transform: Product rule: Increment: Partial derivatives: A new function of two variables: 43

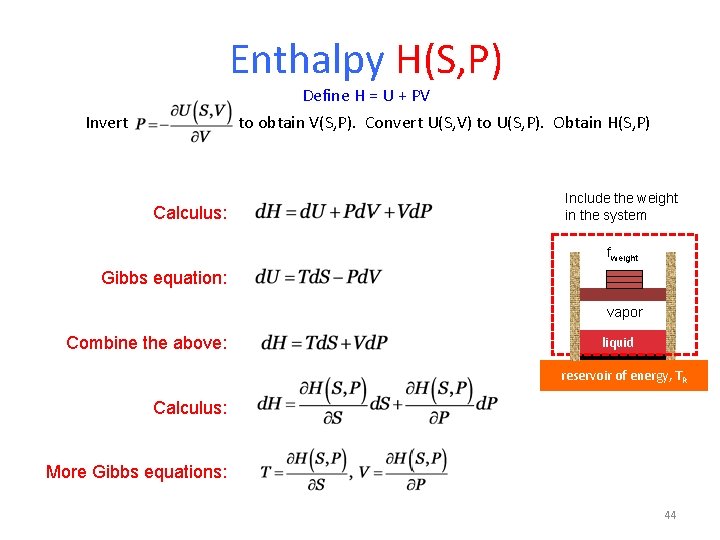
Enthalpy H(S, P) Define H = U + PV to obtain V(S, P). Convert U(S, V) to U(S, P). Obtain H(S, P) Invert Calculus: Include the weight in the system fweight Gibbs equation: vapor Combine the above: liquid reservoir of energy, TR Calculus: More Gibbs equations: 44

Helmholtz function F(T, V) Define F = U - TS Invert to obtain S(T, V). Convert U(T, V) to U(T, P). Obtain F(T, V) Calculus: Gibbs equation: Combine the above: Calculus: More Gibbs equations: 45

Gibbs function G(T, P) Define G = U - TS + PV G = H – TS = F - PV Calculus: Gibbs equation: Combine the above: Calculus: More Gibbs equations: 46

Heat capacity under two conditions fweight O vapor 2 vapor liquid fire 47

Name more partial derivatives Coefficient of thermal expansion: Isothermal compressibility: Joule-Thomson coefficient: 48

Calculus: second derivatives 49

Maxwell relation Gibbs equation: Gibbs relations: Maxwell relation: 50

Mathematical manipulation of dubious value Find a reason to be unhappy with Gibbs equations: Make up a excuse to study a different function: Calculus: Clausius-Gibbs equation: Constant V: Maxwell relation: A pointless equation: 51

Another pointless equation A pointless equation: Gibbs equation: Another pointless equation: 52

Breed thermodynamic properties like rabbits A single function S(U, V) produces all other functions. Inbreeding functions! • Obtain T(U, V) and P(U, V) from the Gibbs equations, • • • Eliminate U from T(U, V) and P(U, V) to obtain P(V, T). Invert S(U, V) to obtain U(S, V). Use Legendre transform of U(S, V) to define H(S, P), F(T, V), G(P, T). Invert T(U, V) to obtain U(T, V). Name lots of partial derivatives: CV(T, V), CP(T, P), a(T, P), b(T, P), m(P, H), … 53

Plan • • A system with variable energy and volume Graphic representations Theory of co-existent phases Theory of ideal gases Theory of osmosis Breed properties and equations of state Basic algorithm of thermodynamics in terms of free energy 54

S(U, V, Y) vapor liquid Y = number of molecules in the vapor • • • Fix U and V, but let Y change. The system is an isolated system with an internal variable Y. Y changes to maximize S(U, V, Y). 55

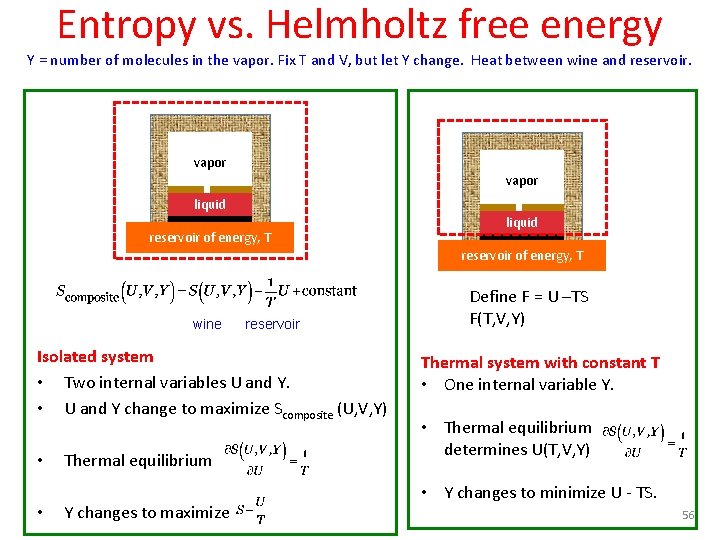
Entropy vs. Helmholtz free energy Y = number of molecules in the vapor. Fix T and V, but let Y change. Heat between wine and reservoir. vapor liquid reservoir of energy, T wine reservoir Isolated system • Two internal variables U and Y. • U and Y change to maximize Scomposite (U, V, Y) • • Thermal equilibrium Y changes to maximize Define F = U –TS F(T, V, Y) Thermal system with constant T • One internal variable Y. • Thermal equilibrium determines U(T, V, Y) • Y changes to minimize U - TS. 56

Entropy vs. Gibbs free energy Y = number of molecules in the vapor. Fix P and T, but let Y change. Energy between wine, weight, reservoir. fweight vapor liquid reservoir of energy, T wine Define G = U - TS + PV G(T, P, Y) reservoir, weight Isolated system • Three internal variables U, V and Y. • U, V and Y change to maximize Scomposite (U, V, Y) Closed system with constant T and P • One internal variable Y. • Thermal equilibrium • Mechanical equilibrium • U(T, P, Y), V(T, P, Y), S(T, P, Y) • Y changes to maximize • Y changes to minimize U-TS +PV. 57

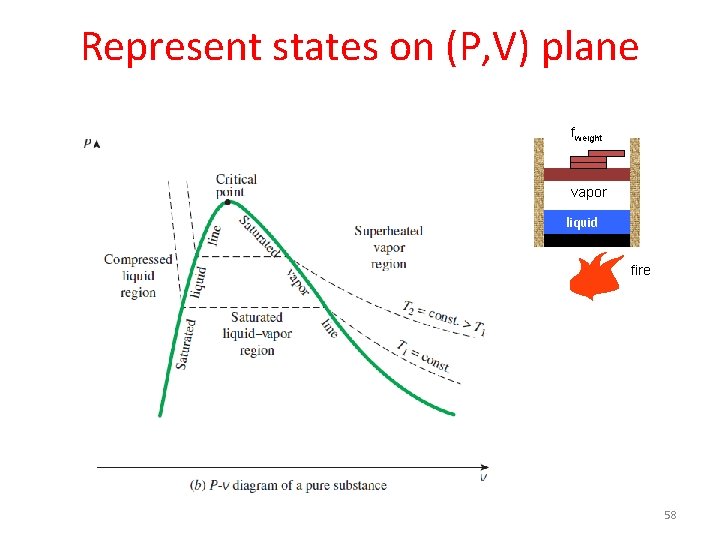
Represent states on (P, V) plane fweight vapor liquid fire 58

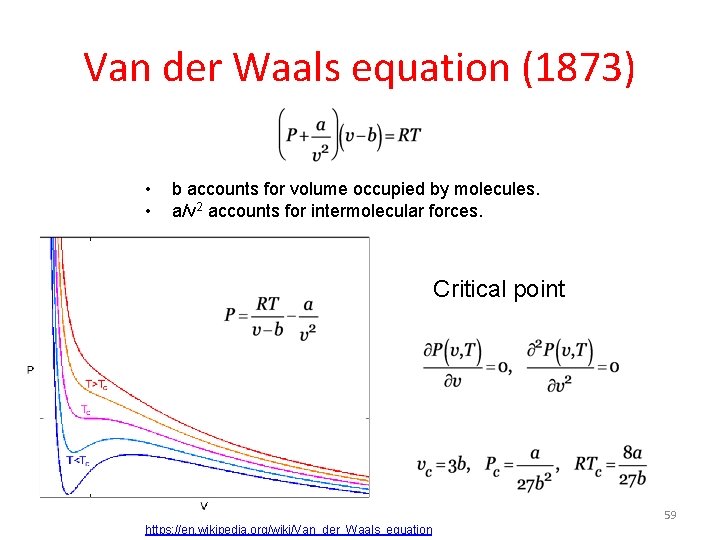
Van der Waals equation (1873) • • b accounts for volume occupied by molecules. a/v 2 accounts for intermolecular forces. Critical point 59 https: //en. wikipedia. org/wiki/Van_der_Waals_equation

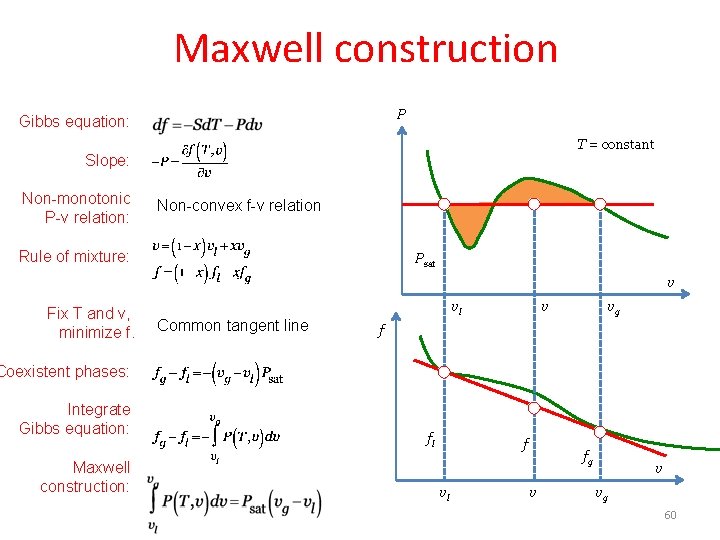
Maxwell construction P Gibbs equation: T = constant Slope: Non-monotonic P-v relation: Non-convex f-v relation Rule of mixture: Psat v Fix T and v, minimize f. Common tangent line vl v vg f Coexistent phases: Integrate Gibbs equation: Maxwell construction: fl f vl fg v v vg 60

Lu and Suo Large conversion of energy in dielectric elastomers by electromechanical phase transition. Acta Mechanica Sinica 28, 1106 -1114 (2012). 61

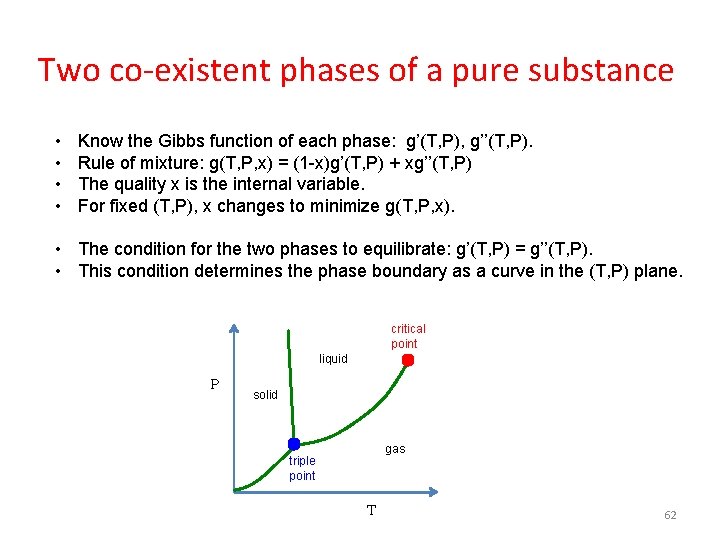
Two co-existent phases of a pure substance • • Know the Gibbs function of each phase: g’(T, P), g’’(T, P). Rule of mixture: g(T, P, x) = (1 -x)g’(T, P) + xg’’(T, P) The quality x is the internal variable. For fixed (T, P), x changes to minimize g(T, P, x). • The condition for the two phases to equilibrate: g’(T, P) = g’’(T, P). • This condition determines the phase boundary as a curve in the (T, P) plane. critical point liquid P solid gas triple point T 62

Claypeyron equation All quantities are for two coexistent phases of a pure substance P liquid gas T Phase boundary: Definition of the Gibbs function: Increment along the phase boundary: Gibbs equation: Claypeyron equation: 63

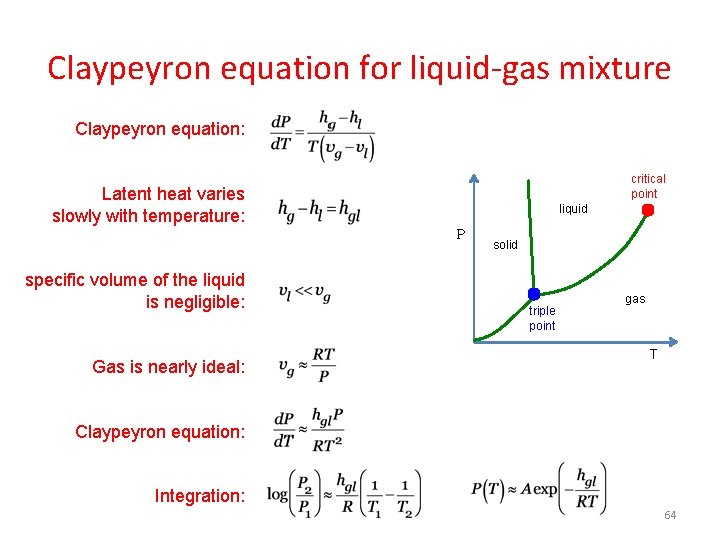
Claypeyron equation for liquid-gas mixture Claypeyron equation: critical point Latent heat varies slowly with temperature: liquid P specific volume of the liquid is negligible: Gas is nearly ideal: solid triple point gas T Claypeyron equation: Integration: 64

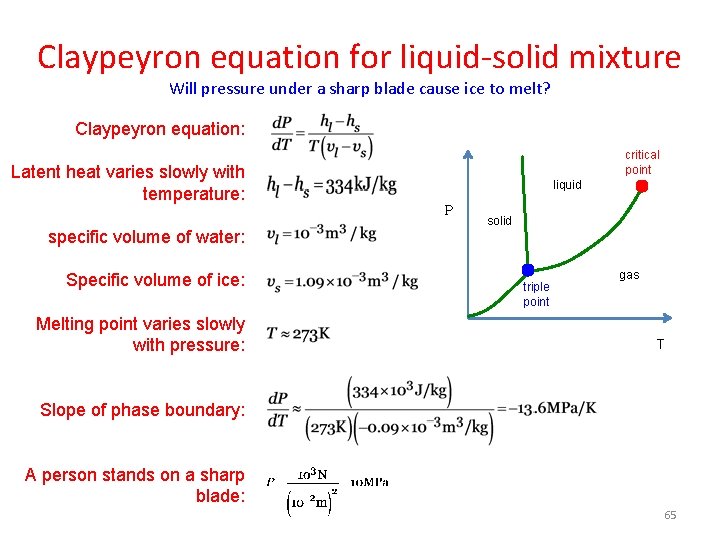
Claypeyron equation for liquid-solid mixture Will pressure under a sharp blade cause ice to melt? Claypeyron equation: Latent heat varies slowly with temperature: specific volume of water: Specific volume of ice: Melting point varies slowly with pressure: critical point liquid P solid triple point gas T Slope of phase boundary: A person stands on a sharp blade: 65

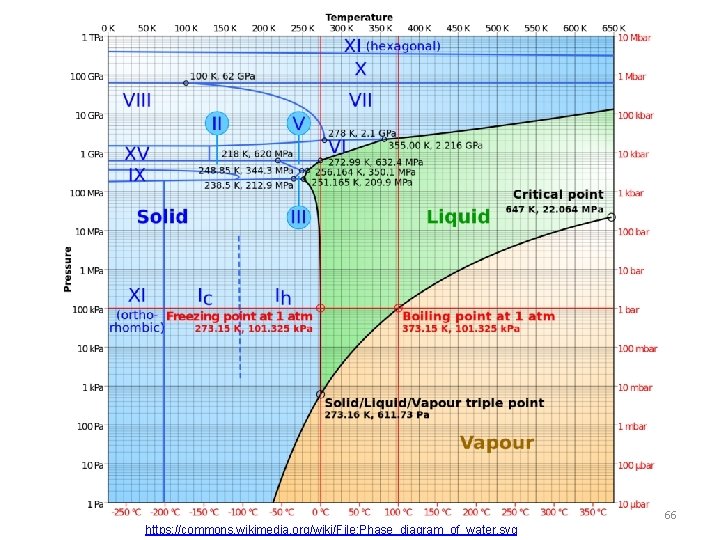
66 https: //commons. wikimedia. org/wiki/File: Phase_diagram_of_water. svg

fweight Summary • Model a closed system as a family of isolated systems. vapor liquid • Gibbs’s thermodynamic surface, S(U, V). • Tangent plane of S(U, V). Gibbs equations • Theory of phases (rule of mixture. convexification. single phases, two coexistent phases, three coexistent phases, critical point). • Ideal gas has two basic equations of state: U(T), PV = Nk. BT. • For a closed system, S(U, V) generates all thermodynamic properties and equations of state (Alternative independent variables, Partial derivatives, Legendre transforms, Maxwell relations). • Basic algorithm of thermodynamics in terms of Gibbs function, G = U - TS - PV. For a closed system of fixed P and T, the internal variable Y changes to minimize G(P, T, Y). 67 fire
 Engineering thermodynamics
Engineering thermodynamics Chemical engineering thermodynamics 8th solution chapter 6
Chemical engineering thermodynamics 8th solution chapter 6 Chemical engineering thermodynamics 8th solution chapter 3
Chemical engineering thermodynamics 8th solution chapter 3 Thermodynamics for chemical engineering
Thermodynamics for chemical engineering Chapter 6
Chapter 6 Thermodynamics : an engineering approach
Thermodynamics : an engineering approach Thermodynamics chapter 2
Thermodynamics chapter 2 Chemical engineering thermodynamics 8th solution chapter 10
Chemical engineering thermodynamics 8th solution chapter 10 Duhem theorem
Duhem theorem Thermodynamics an engineering approach
Thermodynamics an engineering approach Thermodynamics an engineering approach
Thermodynamics an engineering approach Throchlea
Throchlea Pressure support vs pressure control
Pressure support vs pressure control Pressure mapping for pressure ulcers
Pressure mapping for pressure ulcers Intrapulmonary pressure vs intrapleural pressure
Intrapulmonary pressure vs intrapleural pressure Starling's equation
Starling's equation Partial pressure formula
Partial pressure formula Transpulmonary pressure meaning
Transpulmonary pressure meaning Metamorphic
Metamorphic Pressure support vs pressure control
Pressure support vs pressure control Bernoulli equation mass flow rate
Bernoulli equation mass flow rate Oncotic vs hydrostatic pressure
Oncotic vs hydrostatic pressure Interstitial fluid hydrostatic pressure
Interstitial fluid hydrostatic pressure Osmolarity vs osmolality
Osmolarity vs osmolality Oncotic pressure vs hydrostatic pressure
Oncotic pressure vs hydrostatic pressure Dynamothermal
Dynamothermal Adrenaline
Adrenaline How to find partical pressure
How to find partical pressure P support in ventilator
P support in ventilator High pressure and low pressure
High pressure and low pressure High pressure area
High pressure area Microteaching definition
Microteaching definition Btec level 2 information and creative technology
Btec level 2 information and creative technology Computer based system engineering in software engineering
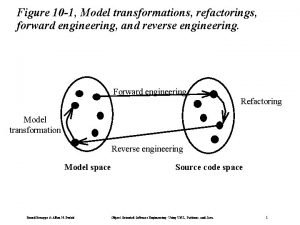
Computer based system engineering in software engineering Forward engineering in software engineering
Forward engineering in software engineering Dicapine
Dicapine Elegant systems
Elegant systems Reverse engineering vs forward engineering
Reverse engineering vs forward engineering Pressure is state function or path function
Pressure is state function or path function Thermodynamics ppt
Thermodynamics ppt Rubbing hands together energy
Rubbing hands together energy Property tables thermodynamics
Property tables thermodynamics Entropy equation temperature
Entropy equation temperature Nozzle and diffuser
Nozzle and diffuser Sssf thermodynamics
Sssf thermodynamics Thermodynamics deals with
Thermodynamics deals with Third tds equation
Third tds equation Thermodynamic probability ppt
Thermodynamic probability ppt Thermodynamic
Thermodynamic Newtons third law of thermodynamics
Newtons third law of thermodynamics Thermodynamics laws
Thermodynamics laws Isobaric process formula
Isobaric process formula Brayton cycle process
Brayton cycle process Residual properties in thermodynamics
Residual properties in thermodynamics Laws of thermodynamics simple
Laws of thermodynamics simple Statistical thermodynamics is a study of
Statistical thermodynamics is a study of Ronald temple
Ronald temple What is reversible process
What is reversible process Change in entropy formula
Change in entropy formula Thermodynamics equation sheet
Thermodynamics equation sheet Van't hoff reaction isotherm
Van't hoff reaction isotherm Refrigeration cycle thermodynamics
Refrigeration cycle thermodynamics Entropy thermodynamics
Entropy thermodynamics Pure substance thermodynamics
Pure substance thermodynamics Thermodynamics study guide
Thermodynamics study guide Maxwell relations applications
Maxwell relations applications State second law of thermodynamics
State second law of thermodynamics Joule's first law of thermodynamics
Joule's first law of thermodynamics