THERMODYNAMICS THERMODYNAMICS HEAT WORK THERMODYNAMICS Two common ways

THERMODYNAMICS

THERMODYNAMICS HEAT & WORK

THERMODYNAMICS Two common ways are Heat Work The energy of a system may increase or decrease in several ways

THERMODYNAMICS Heat (q) Ø It is a form of energy which flows from one system to another because of the difference in temperature. Sign Convention : When heat is absorbed… q is positive When heat is released … q is negative Heat refers to random form of energy

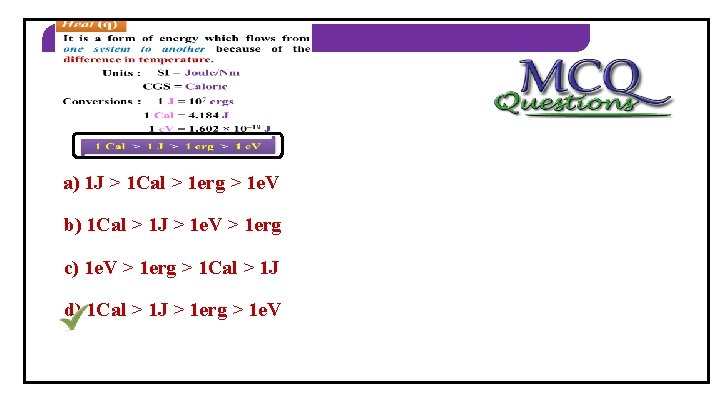
THERMODYNAMICS Heat (q) Ø It is a form of energy which flows from one system to another because of the difference in temperature. Units : SI = Joule/Nm CGS = Calorie Conversions : 1 J = 107 ergs 1 Cal = 4. 184 J 1 e. V = 1. 602 × 10– 19 J 1 Cal > 1 J > 1 erg > 1 e. V Heat refers to random form of energy

THERMODYNAMICS Work (W) : Work is a form of energy transfers from the system to the surroundings or from the surroundings to the system. Types of Work : Work refers to organized form of energy 1. Mechanical work 2. Electrical work 3. Gravitational work Sign Convention : When work is done on the system… W is positive When work is done by the system… W is negative

THERMODYNAMICS Work (W) : Work is a form of energy transfers from the system to the surroundings or from the surroundings to the system. Units : SI = Joule/Nm CGS = Erg / dyne cm Conversions : 1 J = 107 ergs 1 Cal = 4. 184 J 1 e. V = 1. 602 × 10– 19 J 1 L-atm = 101. 3 J 1 L-atm = 24. 22 Cal Work refers to organized form of energy

THERMODYNAMICS 1) When heat is absorbed, its sign convention is… a) positive b) negative c) positive / negative d) none of these

THERMODYNAMICS 2) Identify the correct order a) 1 J > 1 Cal > 1 erg > 1 e. V b) 1 Cal > 1 J > 1 e. V > 1 erg c) 1 e. V > 1 erg > 1 Cal > 1 J d) 1 Cal > 1 J > 1 erg > 1 e. V

THERMODYNAMICS INTERNAL ENERGY AS A STATE FUNCTION

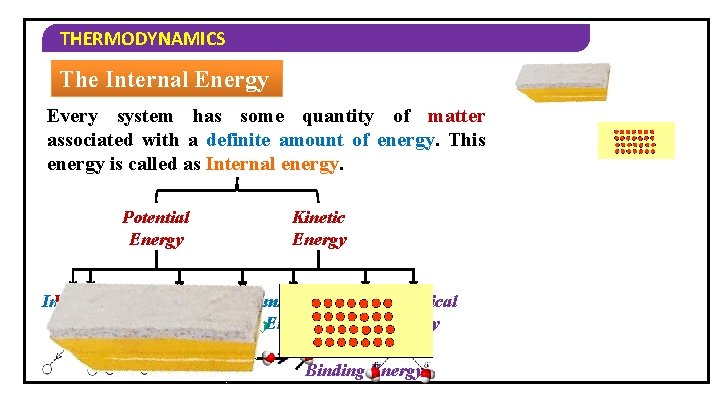
THERMODYNAMICS The Internal Energy Every system has some quantity of matter associated with a definite amount of energy. This energy is called as Internal energy. Potential Energy Kinetic Energy Intermolecular Vibrational Rotational Intramolecular Translational. Nuclear Electronical Energy Or Binding Energy

THERMODYNAMICS Characteristic of Internal Energy ( U ) : 1. It is an extensive property. 2. It is a state function. 3. It. The is not dependent onsystem path followed. property of the whose depends only on and final 4. value There is no change ininitial the internal energy in a cyclic process. state is called as state function 5. Internal energy of an ideal gas is a A system undergoing series of process, function of temperature only. once again returns to its original state is Units – called joulesas(SI) andprocess ergs (CGS) cyclic

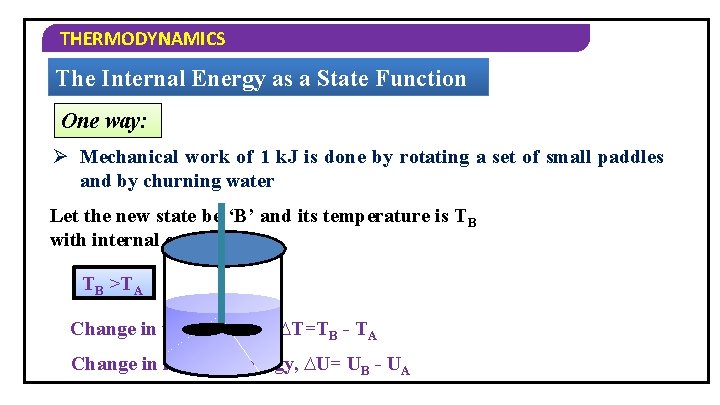
THERMODYNAMICS The Internal Energy as a State Function Let us see the change in internal energy by doing work 1 Take a system containing some quantity of water in an insulated thermos flask. 2 Let us bring the change in the internal energy of the system by doing some work on it. 3 Let us call the initial state of the system as state A, its temperature as Ta and internal energy as UA.

THERMODYNAMICS The Internal Energy as a State Function We can change the state of the system in two different ways.

THERMODYNAMICS The Internal Energy as a State Function One way: Ø Mechanical work of 1 k. J is done by rotating a set of small paddles and by churning water Let the new state be ‘B’ and its temperature is TB with internal energy is UB. TB >TA Change in temperature, ∆T=TB - TA Change in internal energy, ∆U= UB - UA

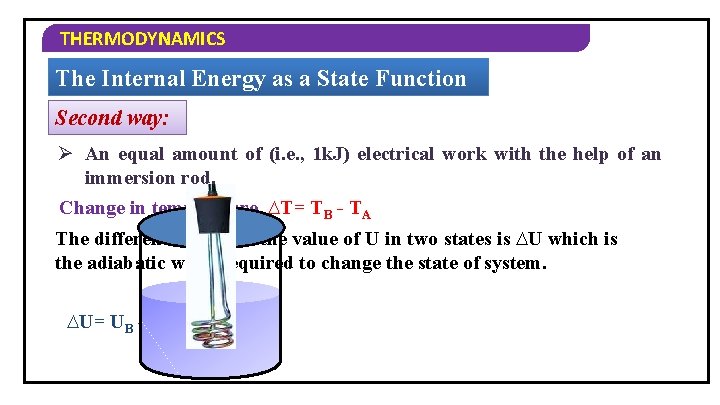
THERMODYNAMICS The Internal Energy as a State Function Second way: Ø An equal amount of (i. e. , 1 k. J) electrical work with the help of an immersion rod. Change in temperature, ∆T= TB - TA The difference between the value of U in two states is ∆U which is the adiabatic work required to change the state of system. ∆U= UB – UA = wad

THERMODYNAMICS The Internal Energy as a State Function Conclusion: The change in the internal energy is same in the above experiments, i. e. , internal energy is a state function.

THERMODYNAMICS 1) Internal energy does not include… a) Vibrational energy b) Rotational energy c) Energy arising by gravitational pull d) Nuclear energy

THERMODYNAMICS 2) Types of potential energy are… a) intermolecular b) intramolecular c) binding d) all of these

THERMODYNAMICS EXPRESSION FOR ISOTHERMAL WORK DONE

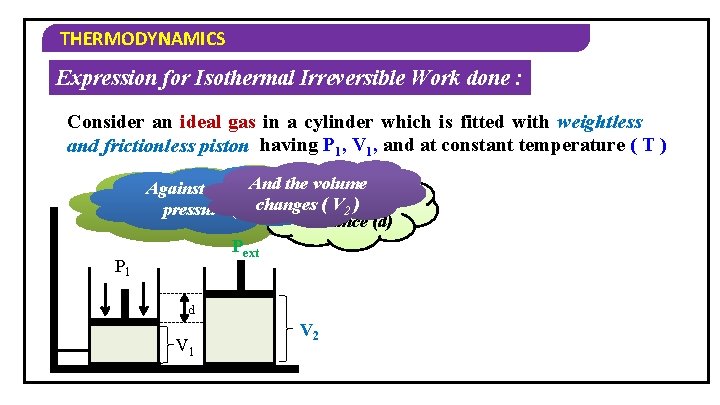
THERMODYNAMICS Expression for Isothermal Irreversible Work done : Consider an ideal gas in a cylinder which is fitted with weightless and frictionless piston having P 1, V 1, and at constant temperature ( T ) And the volume Against an external If the gas expands, it pushes Through changes ( V 2 ) a pressure ( P ) ext the piston upwards distance (d) Pext P 1 d V 1 V 2

THERMODYNAMICS Expression for Isothermal Irreversible Work done : Consider an ideal gas in a cylinder which is fitted with weightless and frictionless piston having P 1, V 1, and at constant temperature ( T ) Work done (W) = Opposing force Work done (W) = × displacement –f × d Work done (W) =sign… – Pext × A × Negative because it d is an expansion Work done (W) = – Pext × ( V 2 – V 1 ) Work done (W) = – Pext ∆V

THERMODYNAMICS Expression for Isothermal Irreversible Work done : Sign Convention for Work (Expansion & Compression) W = – P∆V During Expansion V 2 > V 1 ∆V is positive W = Negative During Compression V 2 < V 1 ∆V is negative W = Positive

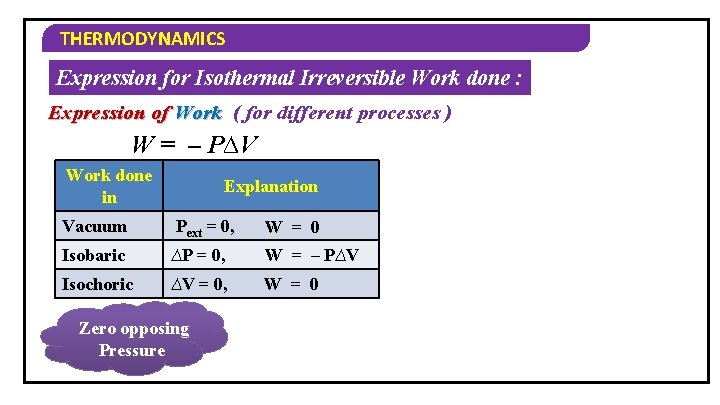
THERMODYNAMICS Expression for Isothermal Irreversible Work done : Expression of Work ( for different processes ) W = – P∆V Work done in Explanation Vacuum Pext = 0, W = 0 Isobaric ∆P = 0, W = – P∆V Isochoric ∆V = 0, W = 0 Zero opposing Pressure

THERMODYNAMICS Formula W P V L – atm L Joules Nm– 2 m 3 Joules Pa m 3 1 lit atm = 24. 22 calories = 101. 3 joules = 101. 3 x 107 ergs 1 joule = 107 ergs = 0. 2389 calories W = – P∆V

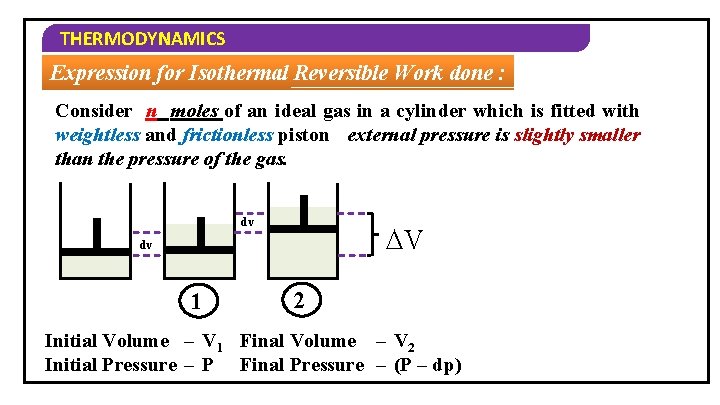
THERMODYNAMICS Expression for Isothermal Reversible Work done : Consider n moles of an ideal gas in a cylinder which is fitted with weightless and frictionless piston external pressure is slightly smaller than the pressure of the gas. dv ∆V dv 1 2 Initial Volume – V 1 Final Volume – V 2 Initial Pressure – P Final Pressure – (P – dp)

THERMODYNAMICS Expression for Isothermal Reversible Work done : W = – Pext ∆V d. W = – Pext d. V But Pext = P – d. P d. W = – (P – d. P) d. V d. W = – Pd. V + d. P. d. V But d. P & d. V are small, hence the product is even smaller. Therefore, neglecting the product d. P. d. V, we get d. W = – Pd. V Work done at

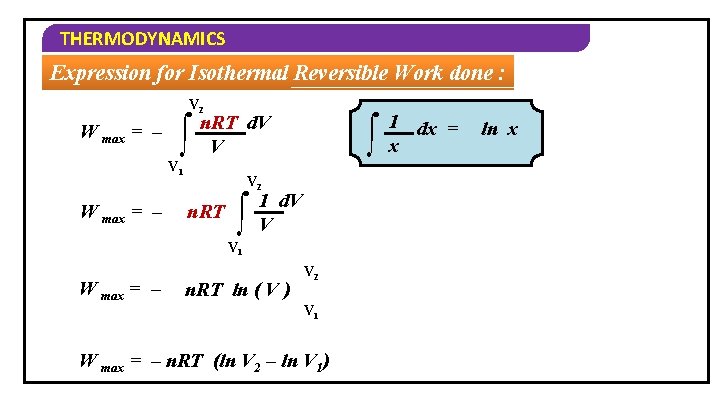
THERMODYNAMICS Expression for Isothermal Reversible Work done : The total work done in the entire expansion from volume V 1 to V 2 will be V 2 2 1 ∫d. W = – ∫Pd. V V 2 V 1 W max = ∫ – Pd. V V 1 The ideal gas equation for n mole of a gas is PV = n. RT Hence P = n. RT V

THERMODYNAMICS Expression for Isothermal Reversible Work done : V 2 W max = – ∫ n. RT d. V V V 1 W max = – ∫ V 2 n. RT ∫ 1 d. V V V 1 W max = – n. RT ln ( V ) V 2 V 1 W max = – n. RT (ln V 2 – ln V 1) 1 dx = x ln x

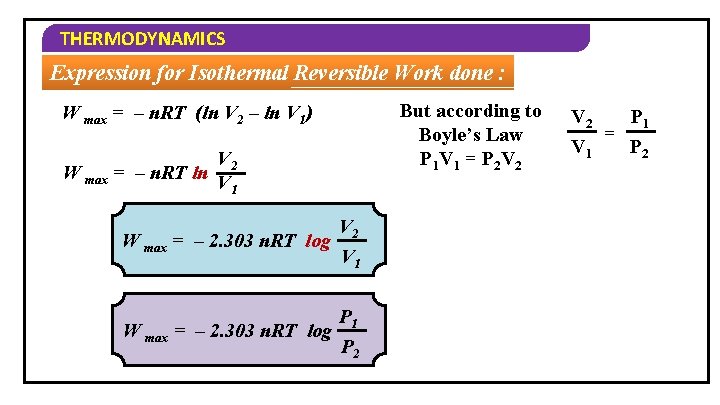
THERMODYNAMICS Expression for Isothermal Reversible Work done : But according to Boyle’s Law P 1 V 1 = P 2 V 2 W max = – n. RT (ln V 2 – ln V 1) W max = – n. RT ln V 2 V 1 W max = – 2. 303 n. RT log V 2 V 1 P 2 V 2 P 1 = P 2 V 1

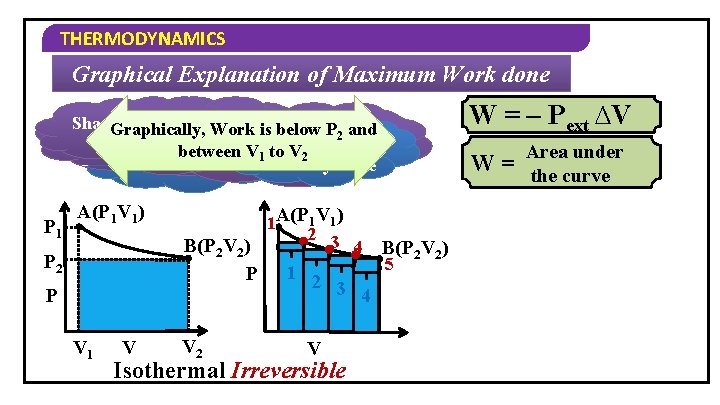
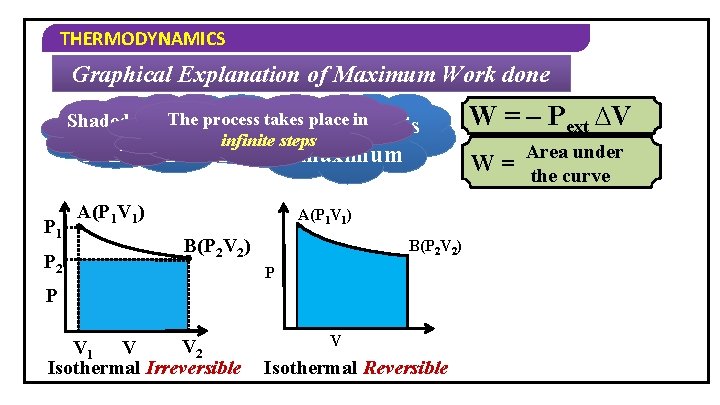
THERMODYNAMICS Graphical Explanation of Maximum Work done Shaded portion Suppose, we consider the Graphically, Work iswe below P 2 and Work isthe Suppose, consider a Suppose, process takes System goes from P = P Work done is W = – P ∆V increases ext final 2 same process 2 V between V 42 steps P –B 1 relatively Vtoingraph place point A todone point more P 1 A(P 1 V 1) B(P 2 V 2) P P 2 P V 1 V V 2 1 A(P 1 V 1) 2 3 4 B(P 2 V 2) 5 1 2 3 4 V Isothermal Irreversible W = – Pext ∆V Area under W = the curve

THERMODYNAMICS Graphical Explanation of Maximum Work done process placedone in Shaded is thetakes Suppose, portion we The consider Work more same process infinite steps is Area under maximum P 1 P 2 A(P 1 V 1) W = the curve A(P 1 V 1) B(P 2 V 2) P P V 2 V 1 V Isothermal Irreversible W = – Pext ∆V V Isothermal Reversible

THERMODYNAMICS 1) Formula of work done is… a) W = – Pext ∆V b) W = – P∆V c) W = – Pd. V d) All of these

THERMODYNAMICS 2) Formula of maximum work done is… a) b) c) d) All of these

THERMODYNAMICS FIRST LAW OF THERMODYNAMICS First Law of Thermodynamics

THERMODYNAMICS First Law of Thermodynamics : 1) Energy can neither be created nor destroyed, only it can be converted from one form to another. 2) The total amount of energy in the Universe remains constant. 3) Whenever a given quantity of energy of one kind disappears, then equivalent amount of energy appears in some other kind. Energy transformation 4) It is not possible for a perpetual motion machine to do work without Energy consuming some form of energy. before after 5) Total energy of an isolated system remains constant. 0

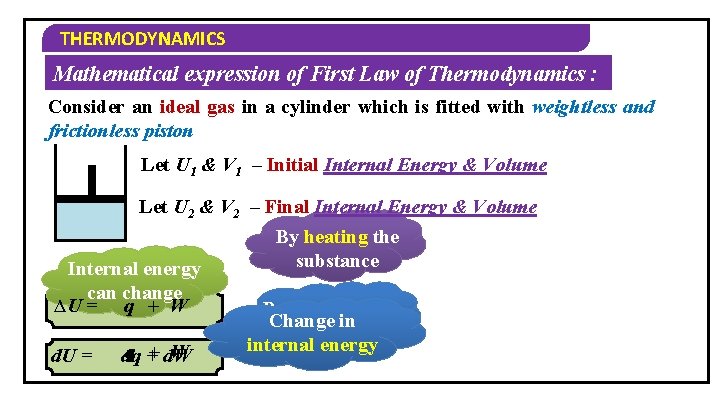
THERMODYNAMICS Mathematical expression of First Law of Thermodynamics : Consider an ideal gas in a cylinder which is fitted with weightless and frictionless piston Let U 1 & V 1 – Initial Internal Energy & Volume Let U 2 & V 2 – Final Internal Energy & Volume By heating the substance Internal energy can change ∆U = q + W d. U = W q + d. W dq By doing work Change in on the system internal energy

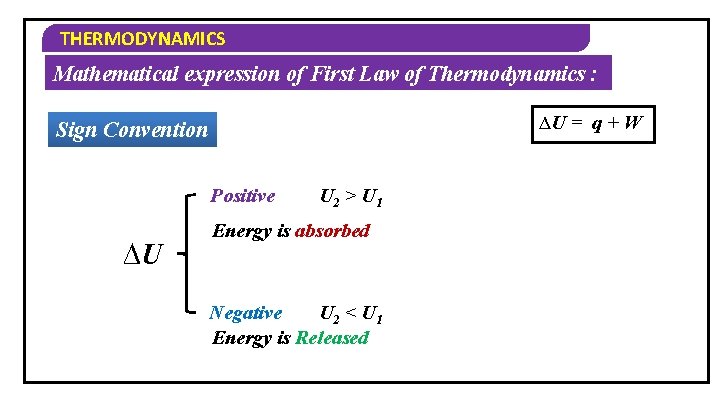
THERMODYNAMICS Mathematical expression of First Law of Thermodynamics : ∆U = q + W Sign Convention Positive ∆U U 2 > U 1 Energy is absorbed Negative U 2 < U 1 Energy is Released

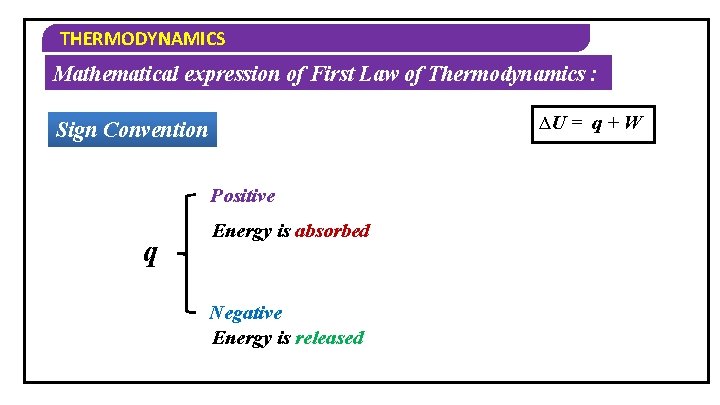
THERMODYNAMICS Mathematical expression of First Law of Thermodynamics : ∆U = q + W Sign Convention Positive q Energy is absorbed Negative Energy is released

THERMODYNAMICS Mathematical expression of First Law of Thermodynamics : ∆U = q + W Sign Convention Compression (On the system) Positive W Expansion Negative (By the system)

THERMODYNAMICS Limitation of First Law of Thermodynamics Ø It does not explain the mass – energy relationship. Ø It does not tell about the direction of flow of energy. Ø It does not tell the spontaneity of the process.

THERMODYNAMICS 1) Limitation of first law of thermodynamics is… a) It does not explain the mass – energy relationship b) It does not tell about the direction of flow of energy c) It does not tell the spontaneity of the process d) All of these

THERMODYNAMICS 2) Mathematical expression of first law of thermodynamics is… a) ∆U = dq + d. W b) q = ∆U + W c) W = ∆U + q d) All of these

THERMODYNAMICS FIRST LAW OF THERMODYNAMICS FOR DIFFERENT PROCESSES

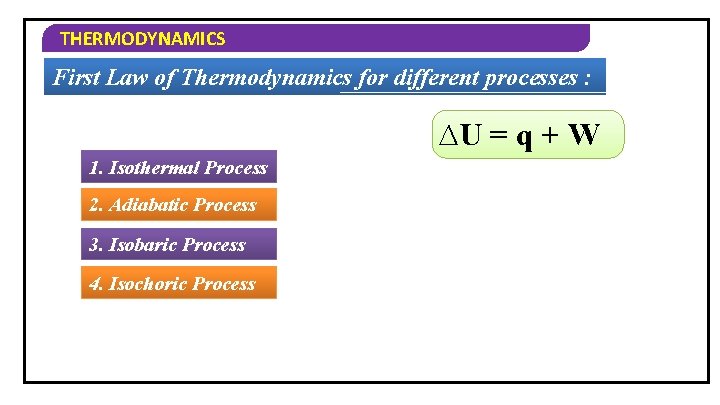
THERMODYNAMICS First Law of Thermodynamics for different processes : ∆U = q + W 1. Isothermal Process 2. Adiabatic Process 3. Isobaric Process 4. Isochoric Process

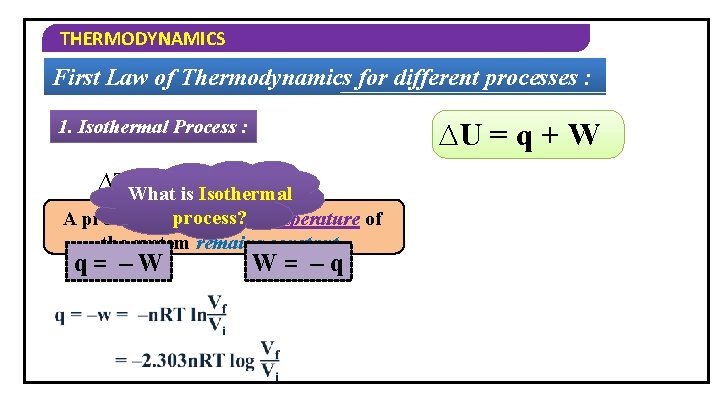
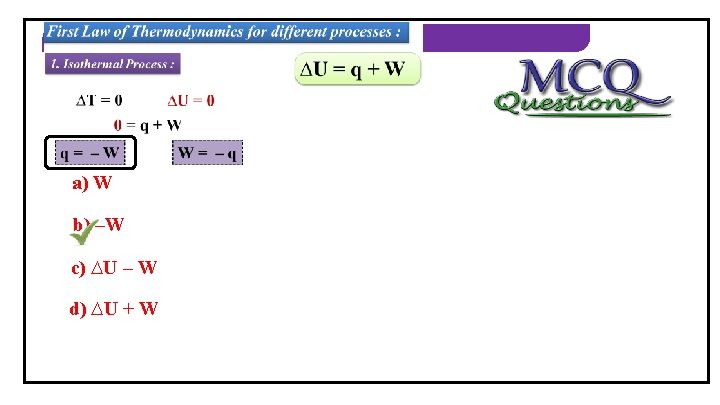
THERMODYNAMICS First Law of Thermodynamics for different processes : 1. Isothermal Process : ∆U = q + W ∆TWhat = 0 is Isothermal ∆U = 0 process? A process in 0 which = q +the Wtemperature of the system remains constant. q= –W W= –q

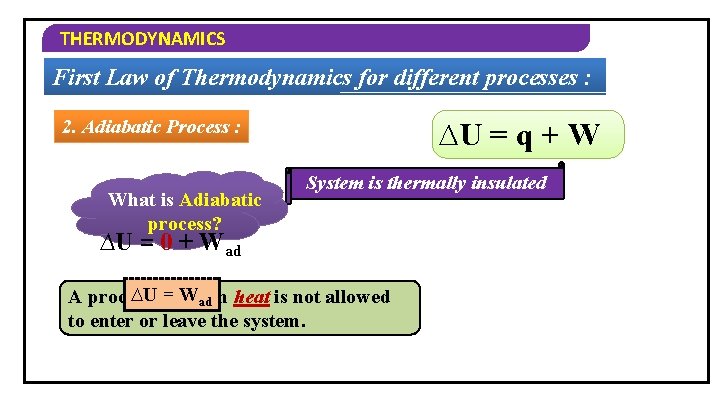
THERMODYNAMICS First Law of Thermodynamics for different processes : 2. Adiabatic Process : q=0 What is Adiabatic ∆U = q + W System is thermally insulated process? ∆U = 0 + Wad ∆Uin= which Wad heat is not allowed A process to enter or leave the system.

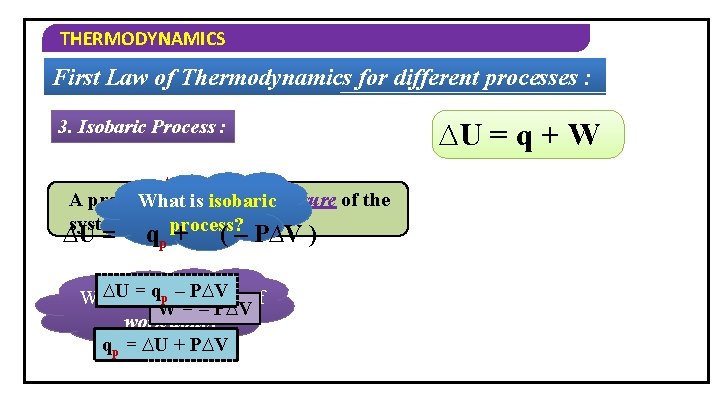
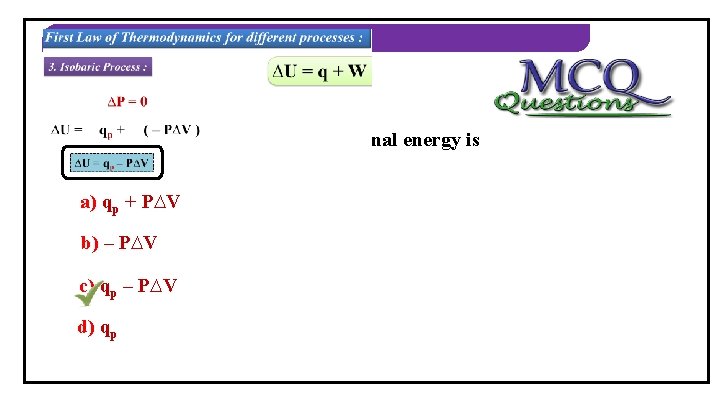
THERMODYNAMICS First Law of Thermodynamics for different processes : 3. Isobaric Process : ∆P = 0 A process in which the pressure of the What is isobaric system remains constant. process? ∆U = qp + ( – P∆V ) ∆Uis=the qp –formula P∆V of What W = – P∆V work done? qp = ∆U + P∆V ∆U = q + W

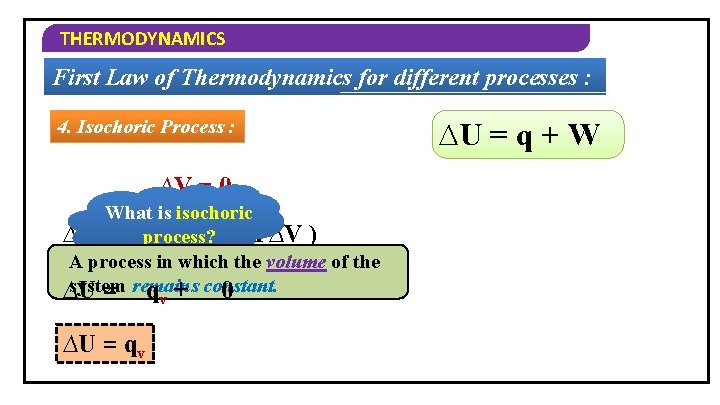
THERMODYNAMICS First Law of Thermodynamics for different processes : 4. Isochoric Process : ∆V = 0 What is isochoric ∆U = process? qv + ( – P∆V ) A process in which the volume of the system ∆U = remains q + constant. 0 v ∆U = q + W

THERMODYNAMICS 1) In isothermal process, q =_____. a) W b) –W c) ∆U – W d) ∆U + W

THERMODYNAMICS 2) In isobaric process, change in internal energy is equal to… a) qp + P∆V b) – P∆V c) qp – P∆V d) qp

THERMODYNAMICS Thank you…