PGT 315 RF AND MICROWAVE TECHNOLOGY CHAPTER 3

PGT 315 RF AND MICROWAVE TECHNOLOGY CHAPTER 3: MICROWAVE NETWORK ANALYSIS

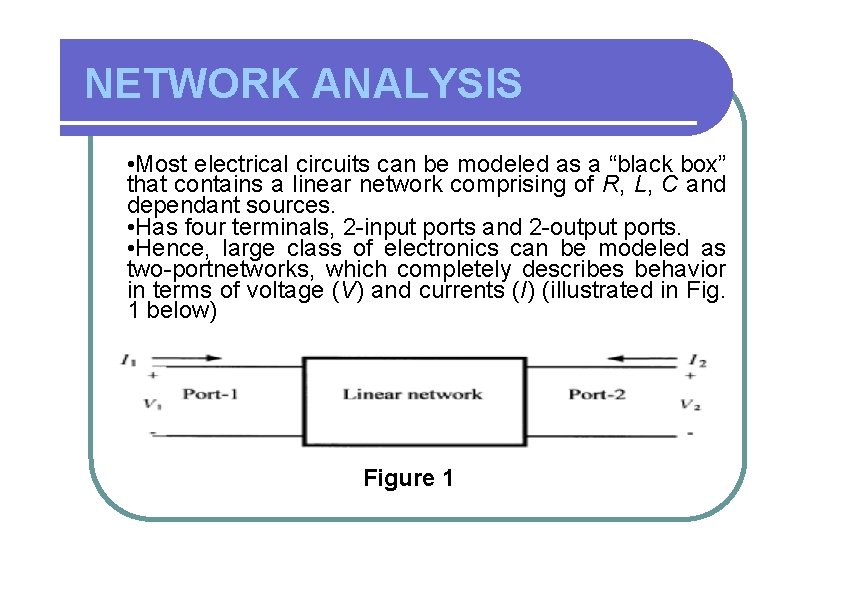
NETWORK ANALYSIS • Most electrical circuits can be modeled as a “black box” that contains a linear network comprising of R, L, C and dependant sources. • Has four terminals, 2 -input ports and 2 -output ports. • Hence, large class of electronics can be modeled as two-portnetworks, which completely describes behavior in terms of voltage (V) and currents (I) (illustrated in Fig. 1 below) Figure 1

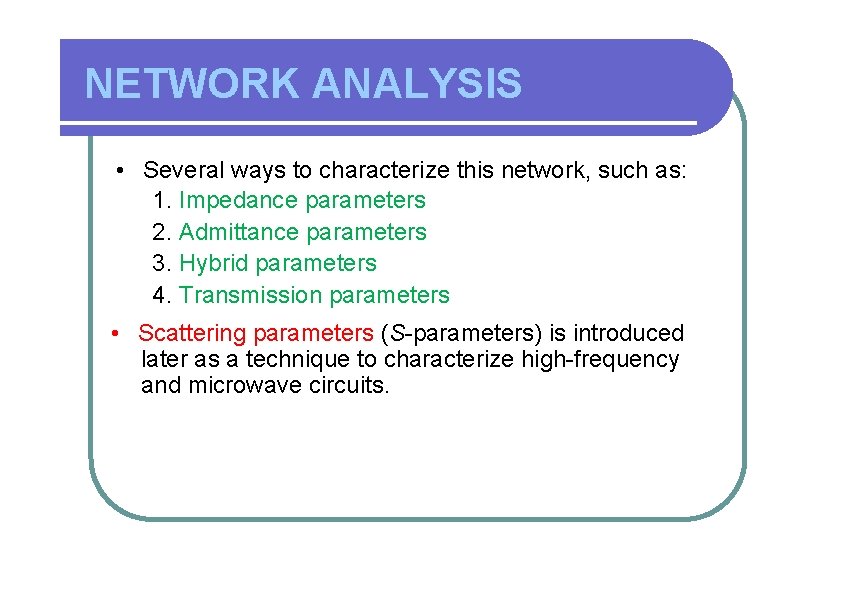
NETWORK ANALYSIS • Several ways to characterize this network, such as: 1. Impedance parameters 2. Admittance parameters 3. Hybrid parameters 4. Transmission parameters • Scattering parameters (S-parameters) is introduced later as a technique to characterize high-frequency and microwave circuits.

NETWORK ANALYSIS Impedance Parameters • Considering Figure 1, considering network is linear, principle of superposition can be applied. Voltage, V 1 at port 1 can be expressed in terms of 2 currents as follow; V 1 = Z 11 I 1 + Z 12 I 2 • Since V 1 is in Volts, I 1 and I 2 are in Amperes, Z 11 and Z 12 must be in Ohms. These are called impedance parameters. • Similarly, for V 2, we can write V 2 in terms of I 1 and I 2 as follow; V 2 = Z 21 I 1 + Z 22 I 2

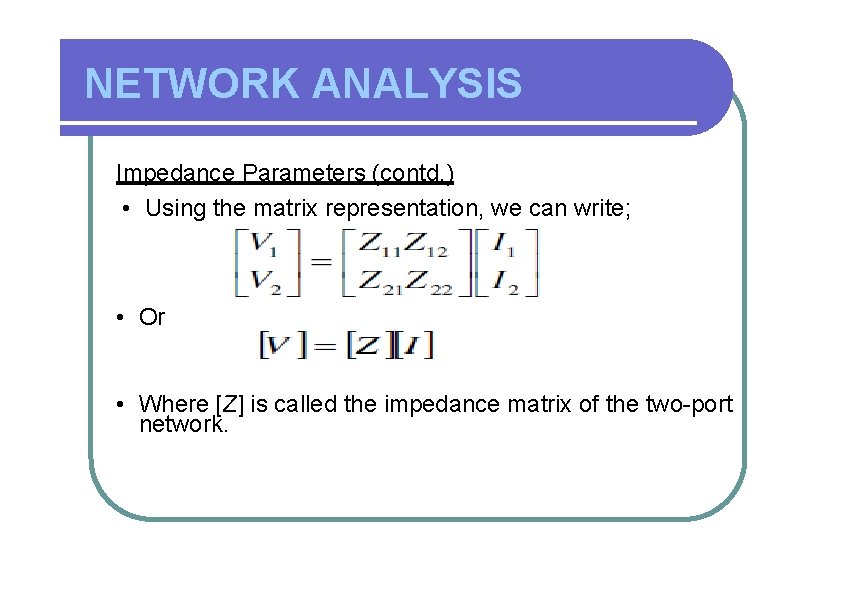
NETWORK ANALYSIS Impedance Parameters (contd. ) • Using the matrix representation, we can write; • Or • Where [Z] is called the impedance matrix of the two-port network.

NETWORK ANALYSIS Impedance Parameters (contd. ) • If port 2 of the network is left open, then I 2 will be zero. In this condition; V 1 V Z 11 = and Z 21 = 2 I 1 I =0 I 1 I 2 =0 2 • Similarly, when port 1 of the network is left open, then I 1 will be zero. In this condition; Z 12 = V 1 I 2 and I 1 =0 V 2 Z 22 = I 2 I 1 =0

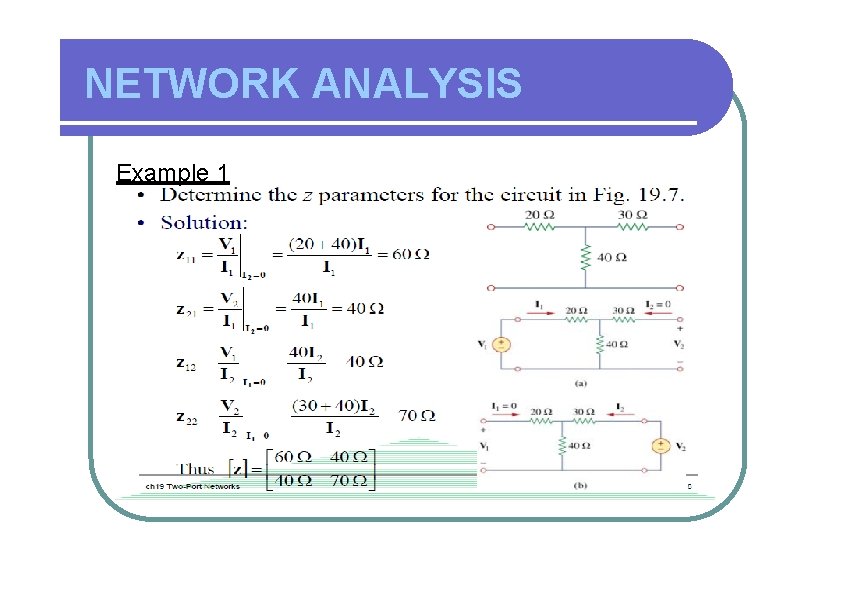
NETWORK ANALYSIS Example 1

NETWORK ANALYSIS Admittance Parameters • Consider again Figure 1. Assuming the network is linear, principle of superposition can be applied. Current, I 1 at port 1 can be expressed in terms of 2 voltages as follow; I 1 = Y 11 V 1+Y 12 V 2 • Since I 1 is in Amperes, V 1 and V 2 are in Volts, Y 11 and Y 12 must be in Siemens. These are called admittance parameters. • Similarly, we can write I 2 in terms of V 1 and V 2 as follow; I 2 = Y 21 V 1+Y 22 V 2

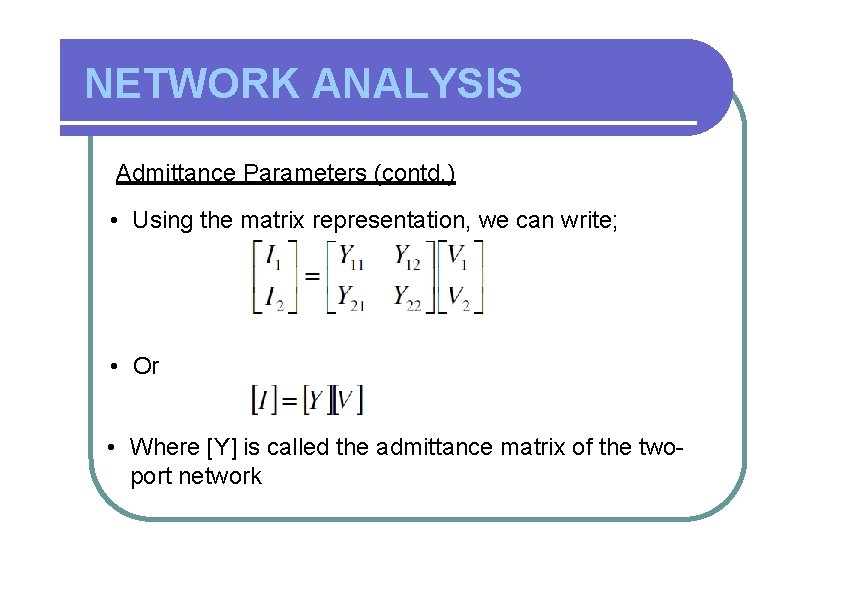
NETWORK ANALYSIS Admittance Parameters (contd. ) • Using the matrix representation, we can write; • Or • Where [Y] is called the admittance matrix of the twoport network

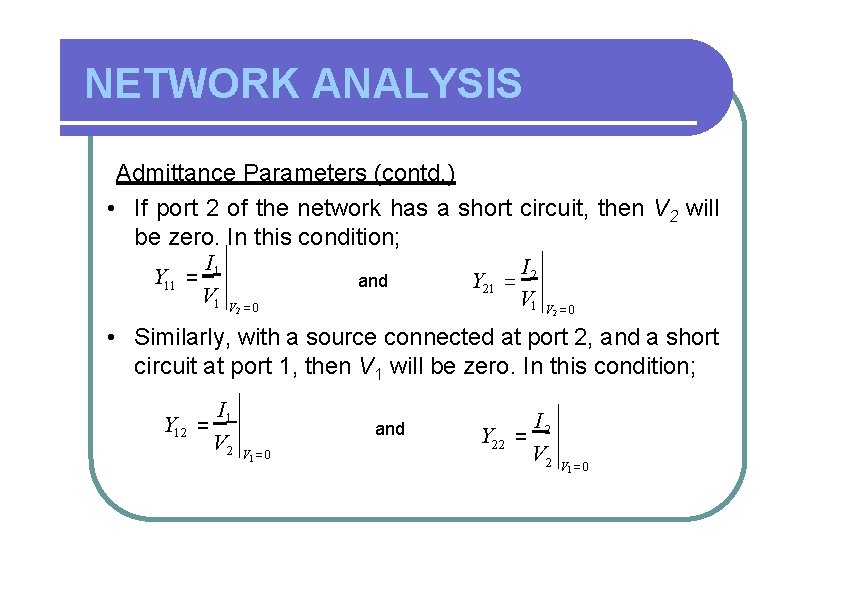
NETWORK ANALYSIS Admittance Parameters (contd. ) • If port 2 of the network has a short circuit, then V 2 will be zero. In this condition; I 1 I Y 11 = and Y 21 = 2 V 1 V =0 2 2 • Similarly, with a source connected at port 2, and a short circuit at port 1, then V 1 will be zero. In this condition; Y 12 = I 1 V 2 and V 1 =0 I 2 Y 22 = V 2 V 1 =0

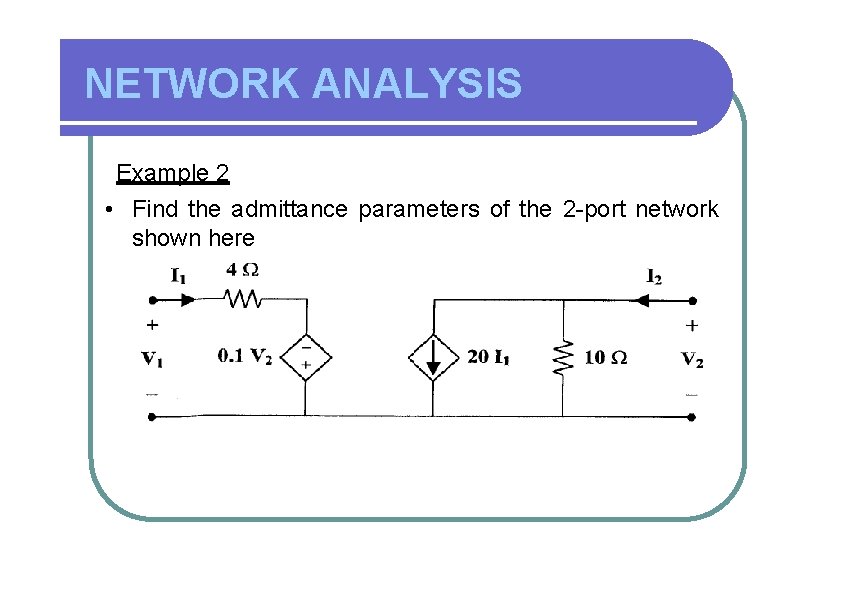
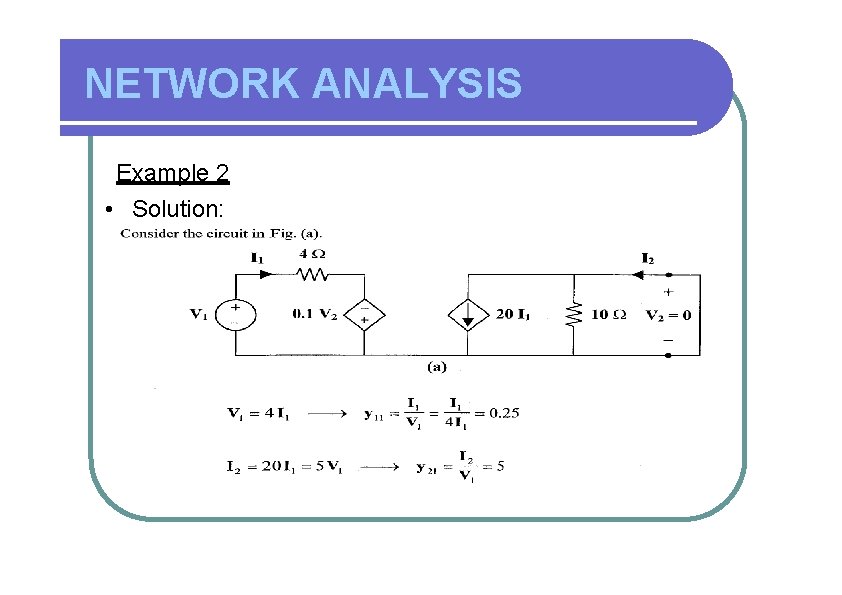
NETWORK ANALYSIS Example 2 • Find the admittance parameters of the 2 -port network shown here

NETWORK ANALYSIS Example 2 • Solution:

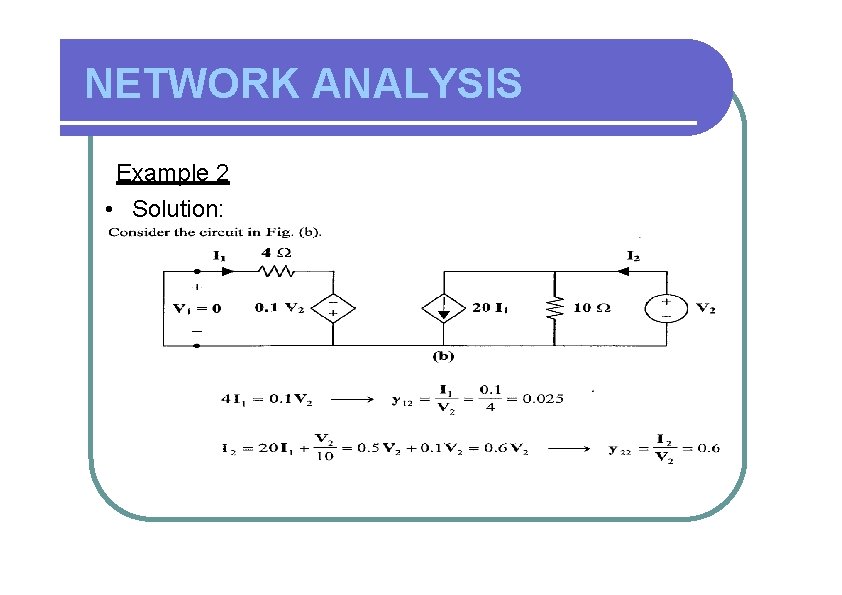
NETWORK ANALYSIS Example 2 • Solution:

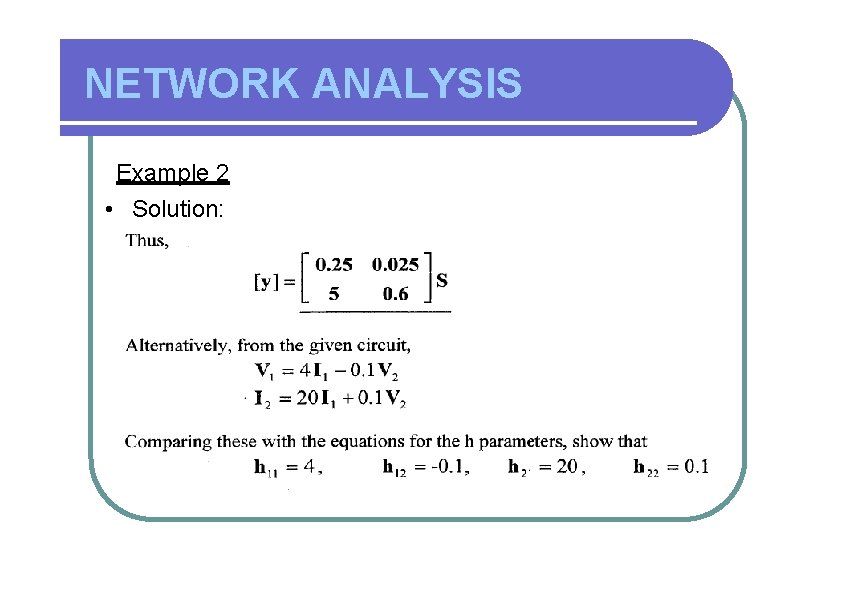
NETWORK ANALYSIS Example 2 • Solution:

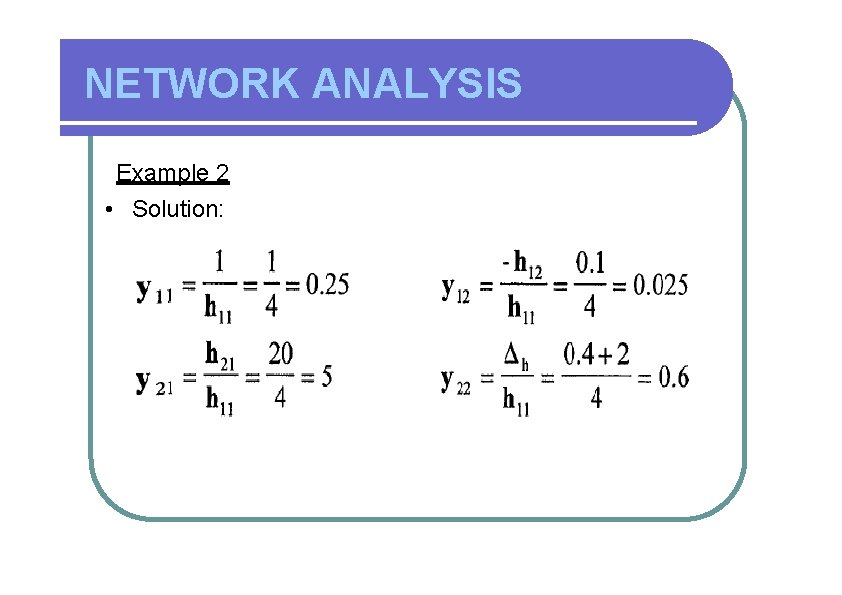
NETWORK ANALYSIS Example 2 • Solution:

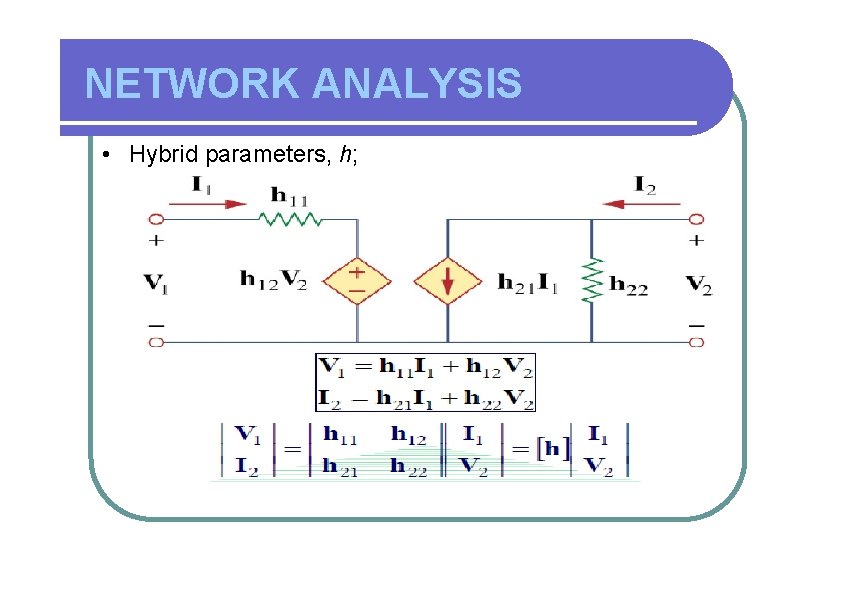
NETWORK ANALYSIS Hybrid Parameters • Consider again Figure 1. Assuming the network is linear, principle of superposition can be applied. Voltage, V 1 at port-1 can be expressed interms of current I 1 at port-2 and voltage V 2 at port-2, as follow; V 1 = h 11 I 1 + h 12 V 2 • Similarly, we can write I 2 in terms of I 1 and V 2 as follow; I 2 = h 21 I 1 + h 22 V 2 • Since V 1 and V 2 are in volts, while I 1 and I 2 are in amperes, parameter h 11 must be in ohms, h 12 and h 21 must be dimensionless, and h 22 must be in Siemens. • These are called hybrid parameters.

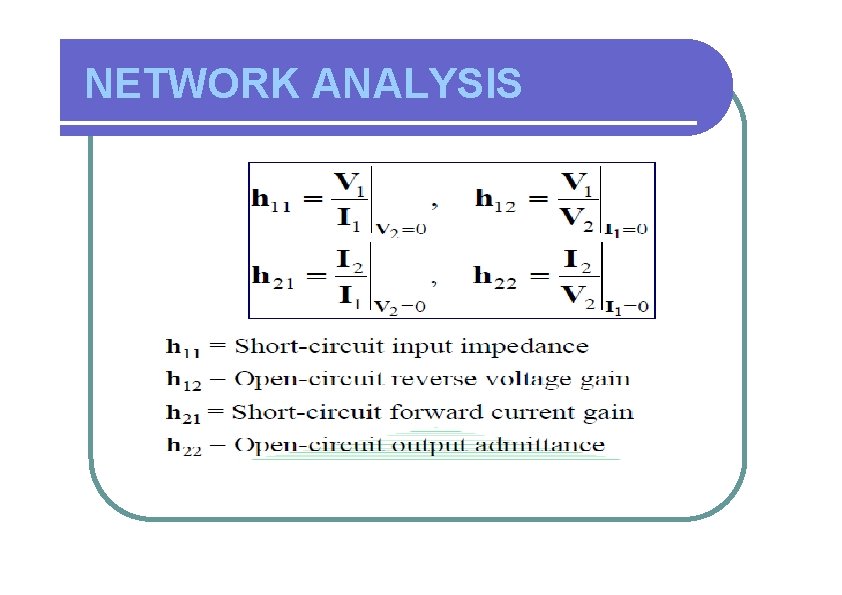
NETWORK ANALYSIS Hybrid Parameters (contd. ) • Using the matrix representation, we can write; • Hybrid parameters are especially important in transistor circuit analysis. The parameters are defined as follow; If port-2 has a short circuit, then V 2 will be zero. • This condition gives; V 1 h 11 = I 1 V 2 =0 and h 21 = I 2 I 1 V 2 =0

NETWORK ANALYSIS Hybrid Parameters (contd. ) • Using the matrix representation, we can write; h 12 = V 1 V 2 and I 1 =0 I 2 h 22 = V 2 I 1 =0 • Hybrid parameters are especially important in transistor circuit analysis. The parameters are defined as follow; If port-2 has a short circuit, then V 2 will be zero. • Similarly, h 12 and h 22 represent reverse voltage gain and the output admittance, respectively, when port-1 has an open circuit. • In circuit analysis, these are generally denoted as hi, hf, hr and ho, respectively.

NETWORK ANALYSIS • Hybrid parameters, h;

NETWORK ANALYSIS

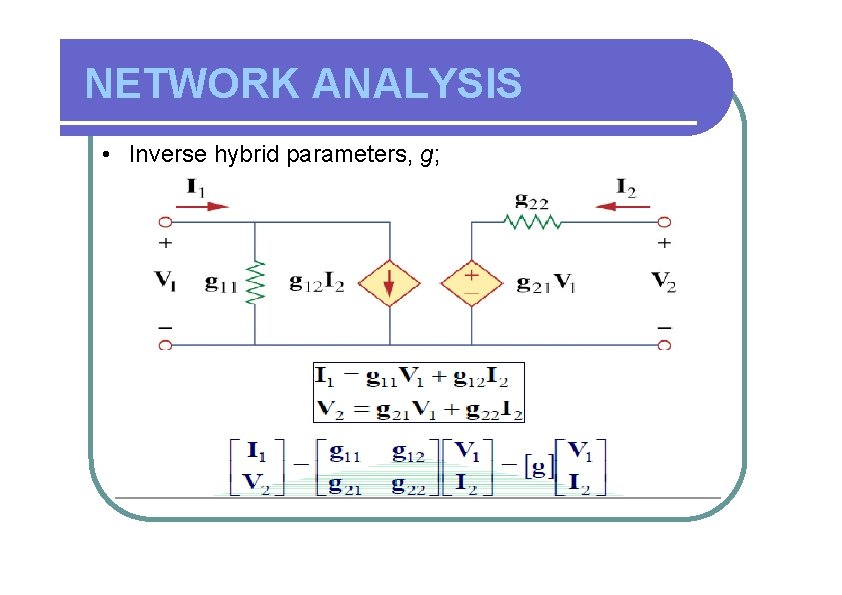
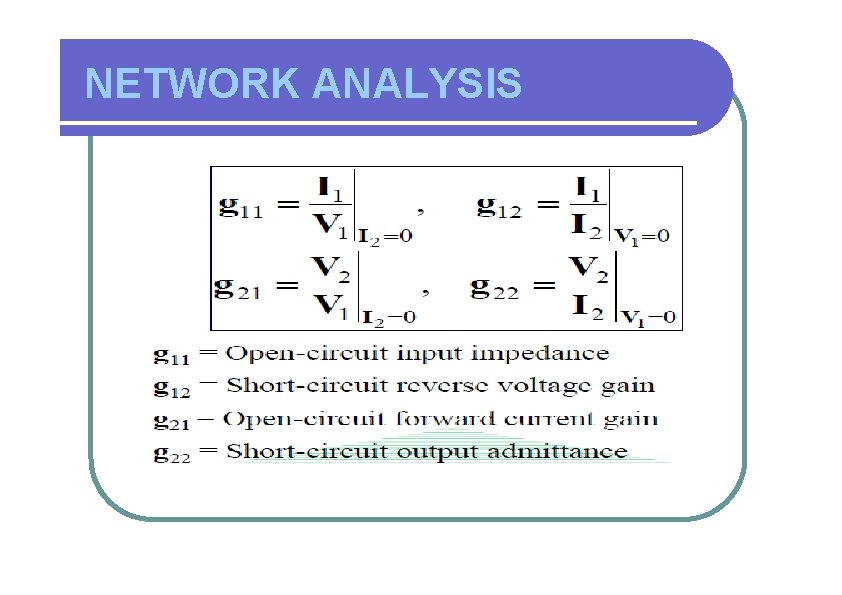
NETWORK ANALYSIS • Inverse hybrid parameters, g;

NETWORK ANALYSIS

NETWORK ANALYSIS Example 3: Hybrid parameters • Find hybrid parameters of the 2 -port network shown here

NETWORK ANALYSIS • Solution:

NETWORK ANALYSIS • Solution:

NETWORK ANALYSIS Transmission Parameters • Consider again Figure 1. Since the network is linear, the superposition principle can be applied. Assuming that it contains no independent sources, Voltage V 1 and current at port 1 can be expressed in terms of current I 2 and voltage V 2 at port-2, as follow; V 1 = AV 2 − BI 2 • Similarly, we can write I 1 in terms of I 2 and V 2 as follow; I 1 = CV 2 − DI 2 • Since V 1 and V 2 are in volts, while I 1 and I 2 are in amperes, parameter A and D must be in dimensionless, B must be in Ohms, and C must be in Siemens.

NETWORK ANALYSIS Transmission Parameters (contd. ) • Using the matrix representation, we can write; • Transmission parameters, also known as elements of chain matrix, are especially important for analysis of circuits connected in cascade. These parameters are determined as follow; If port-2 has a short circuit, then V 2 will be zero. • This condition gives; V B= 1 − I 2 and V 2 =0 I D= 1 − I 2 V 2 =0

NETWORK ANALYSIS Transmission Parameters (contd. ) • Similarly, with a source connected at port-1 while port 2 is open, we find; I 1 V and A= 1 C= V 2 I =0 2 2

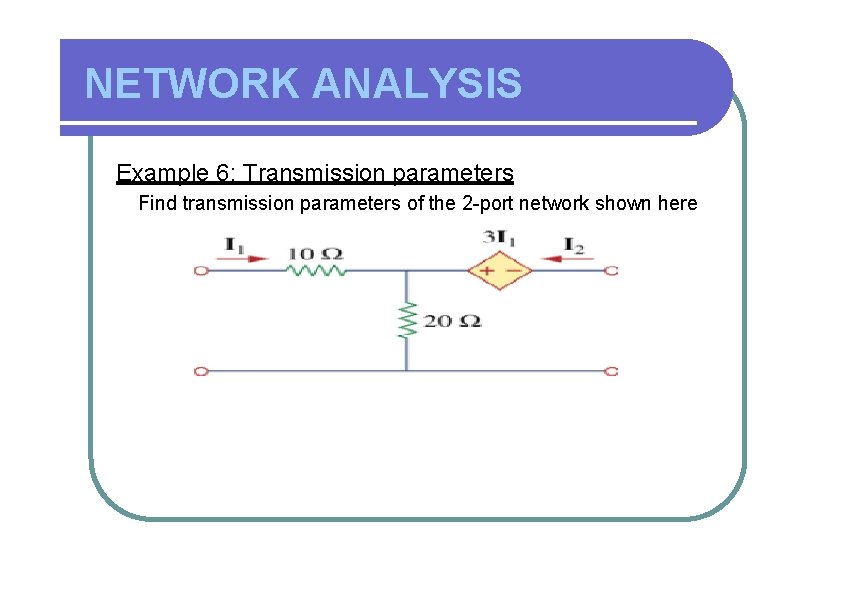
NETWORK ANALYSIS Example 6: Transmission parameters Find transmission parameters of the 2 -port network shown here

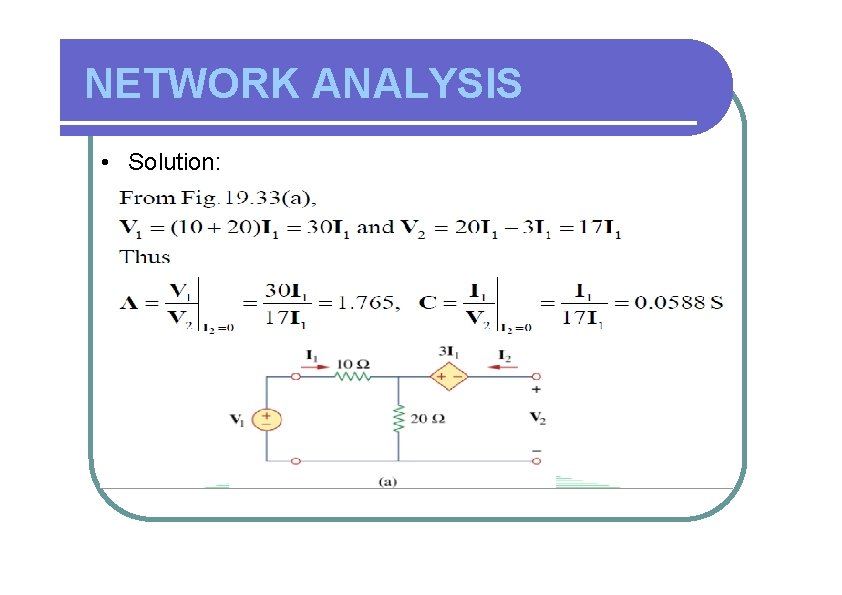
NETWORK ANALYSIS • Solution:

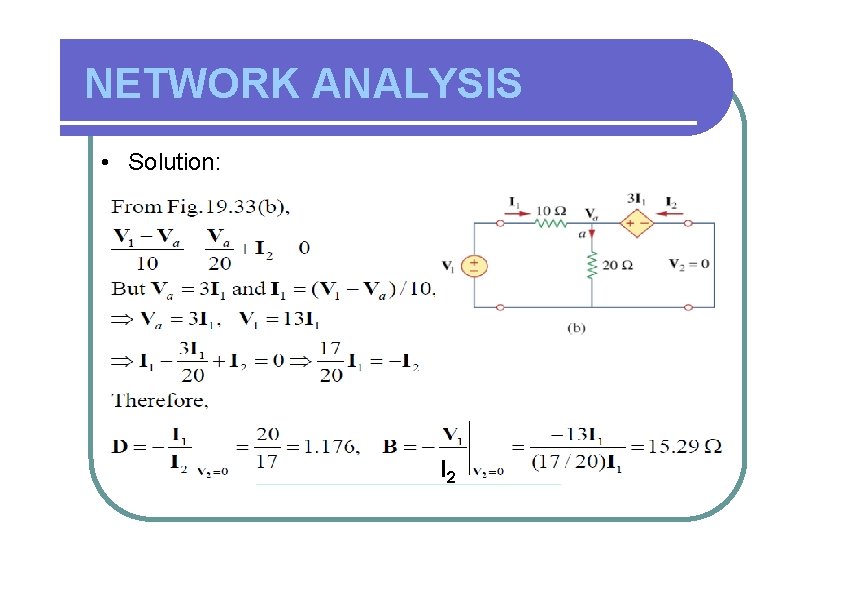
NETWORK ANALYSIS • Solution: I 2

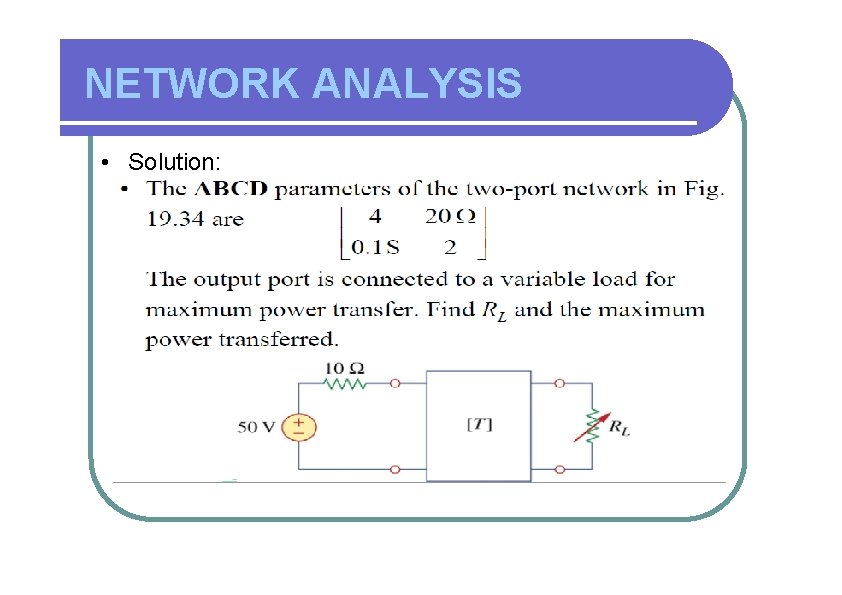
NETWORK ANALYSIS • Solution:

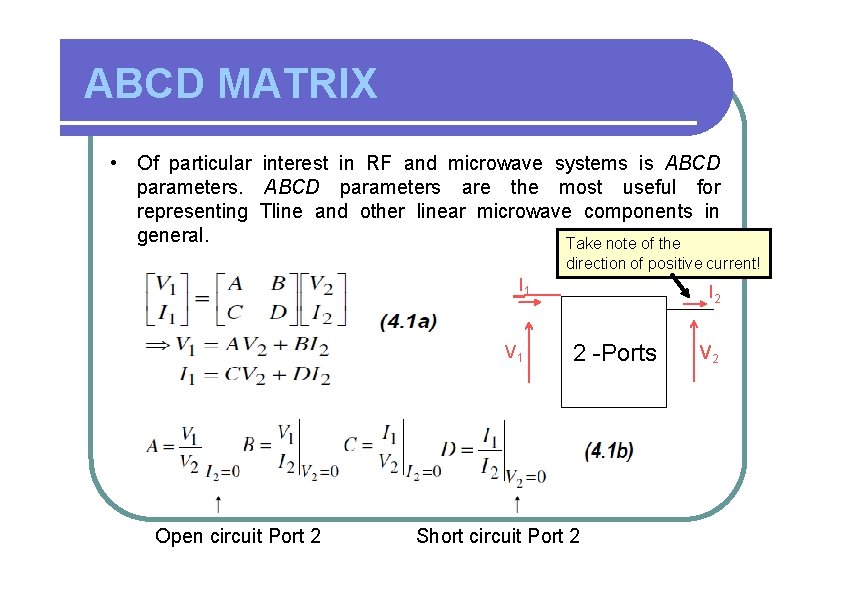
ABCD MATRIX • Of particular interest in RF and microwave systems is ABCD parameters are the most useful for representing Tline and other linear microwave components in general. Take note of the direction of positive current! I 1 V 1 Open circuit Port 2 I 2 2 -Ports Short circuit Port 2 V 2

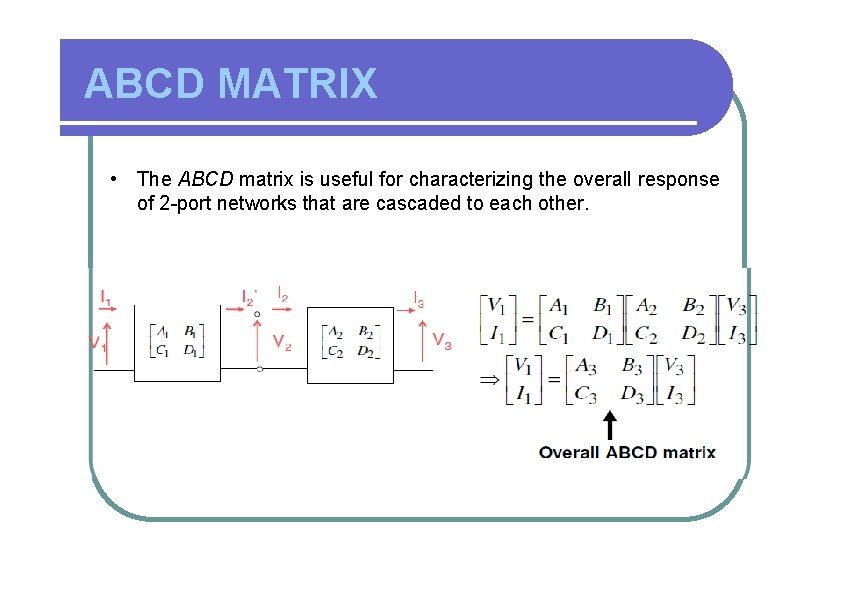
ABCD MATRIX • The ABCD matrix is useful for characterizing the overall response of 2 -port networks that are cascaded to each other.

NETWORK ANALYSIS • Many times we are only interested in the voltage (V) and current (I) relationship at the terminals/ports of a complex circuit. • If mathematical relations can be derived for V and I, the circuit can be considered as a black box. • For a linear circuit, the I-V relationship is linear and can be written in the form of matrix equations. • A simple example of linear 2 -port circuit is shown below. Each port is associated with 2 parameters, the V and I. Convention for positive polarity current and voltage I 1 Port 1 V 1 R I 2 + C V 2 Port 2 -

NETWORK ANALYSIS

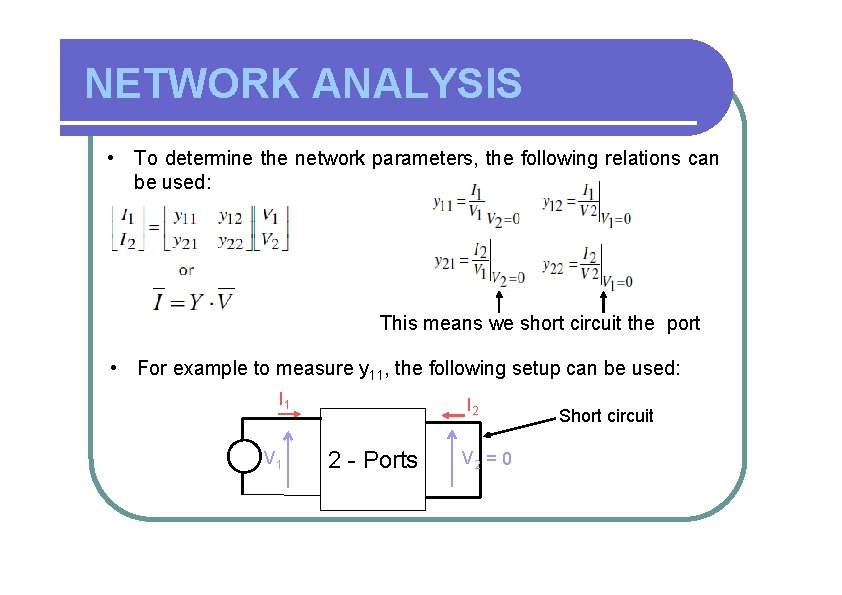
NETWORK ANALYSIS • To determine the network parameters, the following relations can be used: This means we short circuit the port • For example to measure y 11, the following setup can be used: I 1 V 1 I 2 2 - Ports V 2 = 0 Short circuit

NETWORK ANALYSIS • By choosing different combination of independent variables, different network parameters can be defined. This applies to all linear circuits no matter how complex. • Furthermore this concept can be generalized to more than 2 ports, called N - port networks. I 1 V 1 Linear circuit, because all elements have linear I-V relation V 1 I 2 V 2 2 - Ports I 2 V 2

THE SCATTERING MATRIX • Usually we use Y, Z, H or ABCD parameters to describe a linear two port network. • These parameters require us to open or short a network to find the parameters. • At radio frequencies it is difficult to have a proper short or open circuit, there are parasitic inductance and capacitance in most instances. • Open/short condition leads to standing wave, can cause oscillation and destruction of device. • For non-TEM propagation mode, it is not possible to measure voltage and current. We can only measure power from E and H fields.

THE SCATTERING MATRIX • Hence a new set of parameters (S) is needed which § Do not need open/short condition. § Do not cause standing wave. § Relates to incident and reflected power waves, instead of voltage and current. • As oppose to V and I, S-parameters relate the reflected and incident voltage waves. • S-parameters have the following advantages: 1. Relates to familiar measurement such as reflection coefficient, gain, loss etc. 2. Can cascade S-parameters of multiple devices to predict system performance (similar to ABCD parameters). 3. Can compute Z, Y or H parameters from S-parameters if needed.

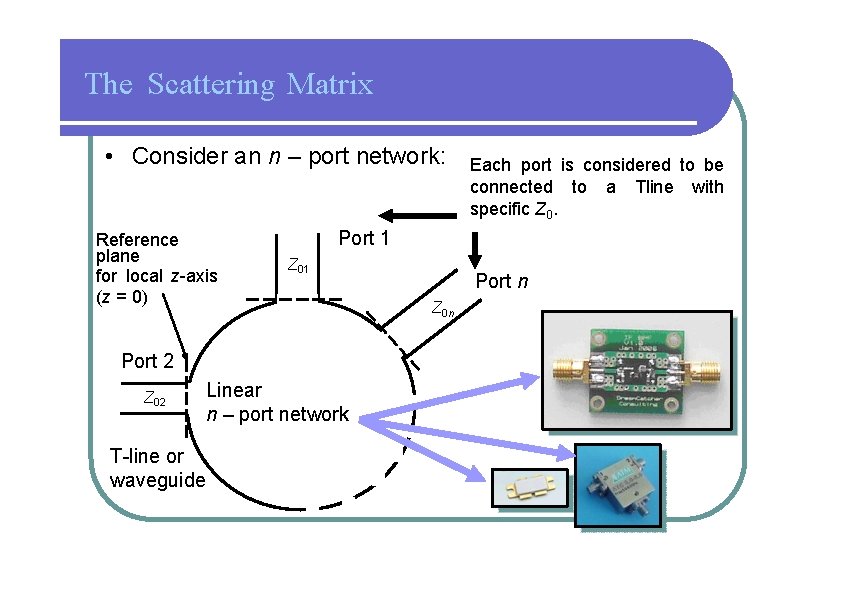
The Scattering Matrix • Consider an n – port network: Reference plane for local z-axis (z = 0) Port 1 Z 01 Port 2 Z 02 Linear n – port network T-line or waveguide Each port is considered to be connected to a Tline with specific Z 0. Port n Z 0 n

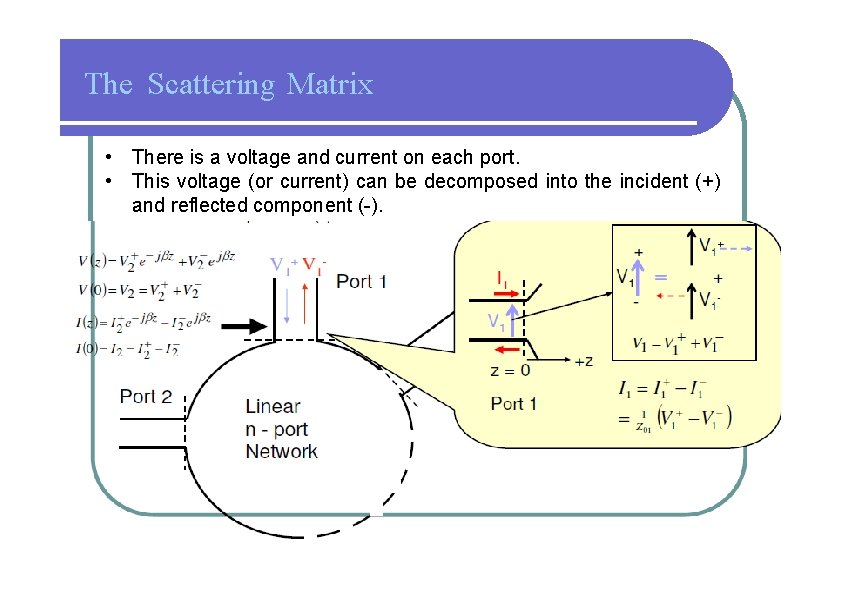
The Scattering Matrix • There is a voltage and current on each port. • This voltage (or current) can be decomposed into the incident (+) and reflected component (-).

The Scattering Matrix • The port voltage and current can be normalized with respect to the impedance connected to it. • It is customary to define normalized voltage waves at each port as: + V Normalized ai = i incident waves (4. 3 a) i = 1, 2, 3 … n Z 0 i + ai =I i Z 0 i − V bi = i Z 0 i − bi =I i Z 0 i Normalized reflected waves (4. 3 b)

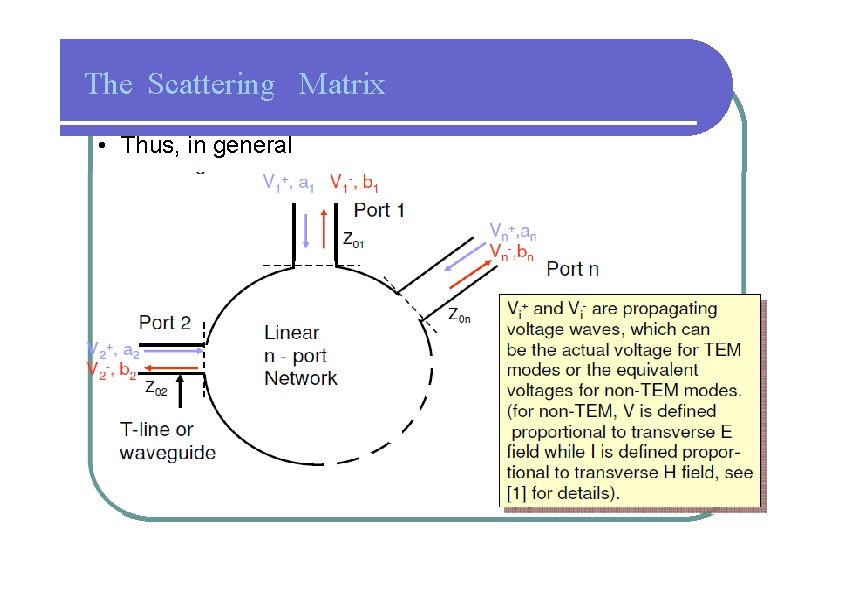
The Scattering Matrix • Thus, in general + -

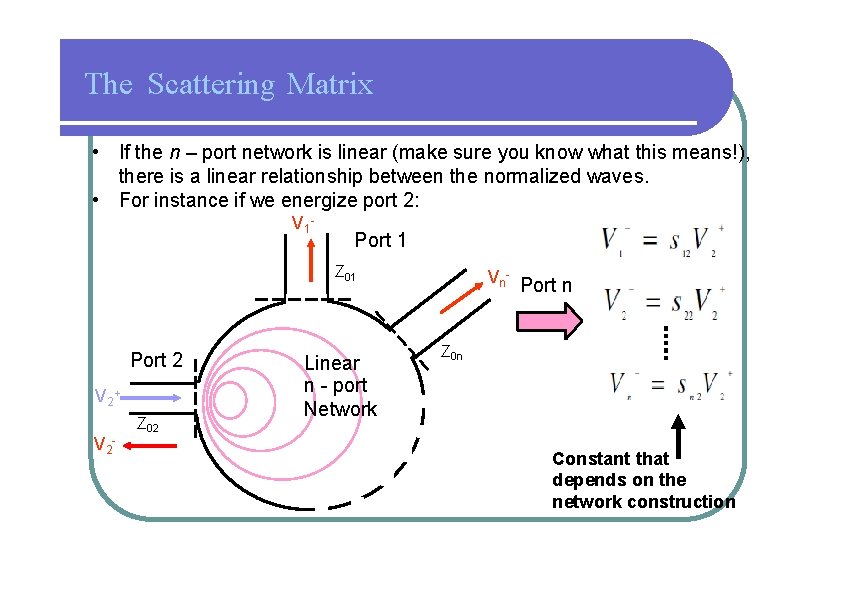
The Scattering Matrix • If the n – port network is linear (make sure you know what this means!), there is a linear relationship between the normalized waves. • For instance if we energize port 2: V 1 - Port 1 Z 01 Port 2 V 2 + V 2 - Z 02 Linear n - port Network Vn- Port n Z 0 n Constant that depends on the network construction

The Scattering Matrix • Considering that we can send energy into all ports, this can be generalized to: • Or written in Matrix equation: • Where sij is known as the generalized Scattering (S) parameter, or just S-parameters for short. From (4. 3), each port i can have different characteristic impedance Z 0 i.

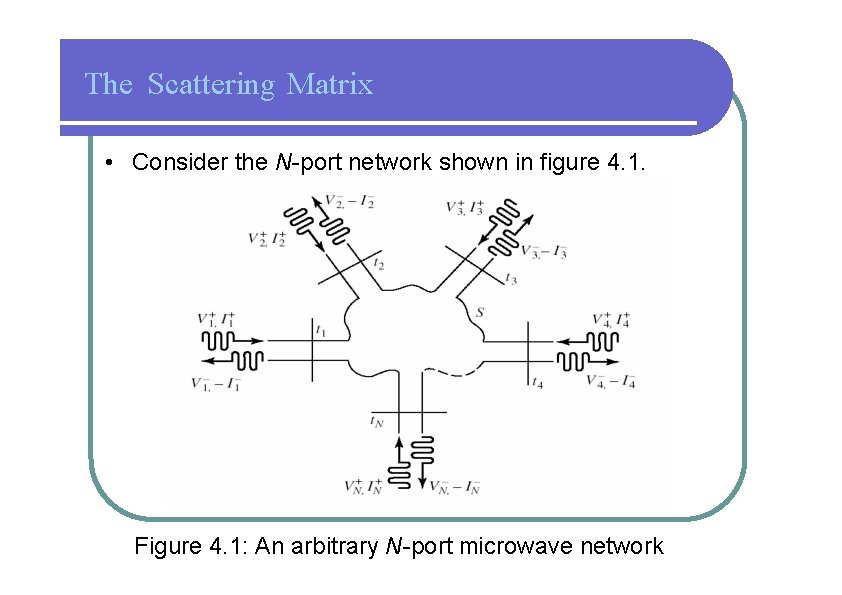
The Scattering Matrix • Consider the N-port network shown in figure 4. 1. Figure 4. 1: An arbitrary N-port microwave network

The Scattering Matrix • Vn+ is the amplitude of the voltage wave incident on port n. • Vn- is the amplitude of the voltage wave reflected from port n. • The scattering matrix or [S] matrix, is defined in relation to these incident and reflected voltage wave as: [4. 1 a]

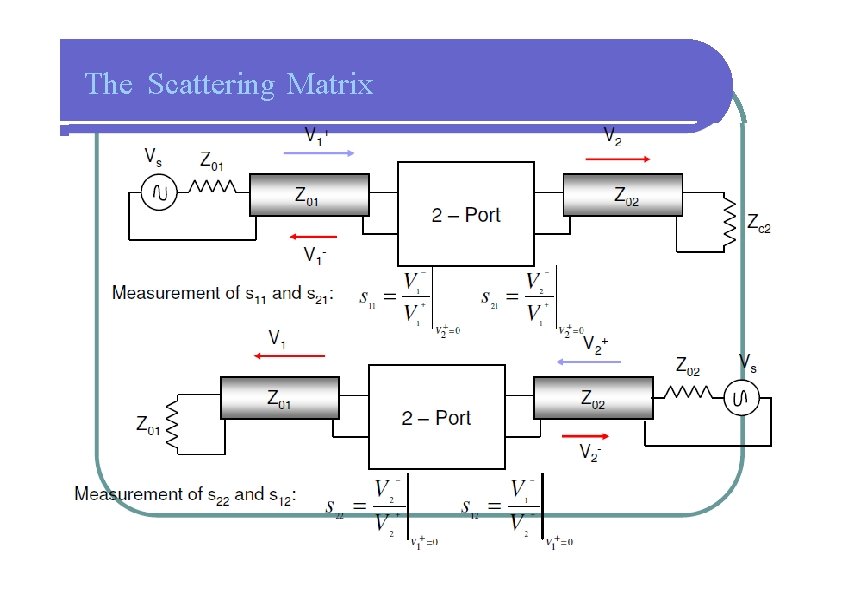
The Scattering Matrix or [V− ] =[S][V+] [4. 1 b] • A specific element of the [S] matrix can be determined as: [4. 2] • Sij is found by driving port j with an incident wave Vj+, and measuring the reflected wave amplitude, Vi-, coming out of port i. • The incident waves on all ports except j-th port are set to zero (which means that all ports should be terminated in matched load to avoid reflections). • Thus, Sii is the reflection coefficient seen looking into port i when all other ports are terminated in matched loads, and Sij is the transmission coefficient from port j to port i when all other ports are terminated in matched loads.

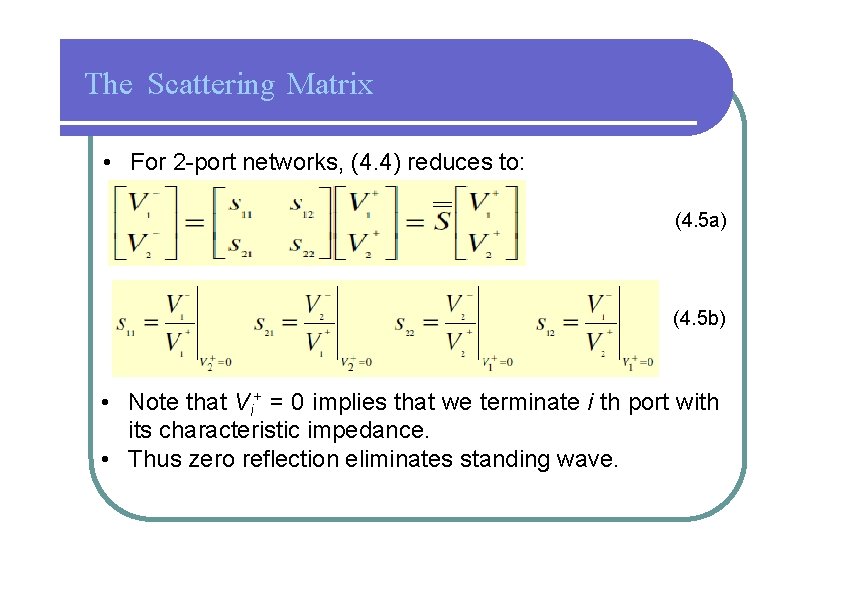
The Scattering Matrix • For 2 -port networks, (4. 4) reduces to: (4. 5 a) (4. 5 b) • Note that Vi+ = 0 implies that we terminate i th port with its characteristic impedance. • Thus zero reflection eliminates standing wave.

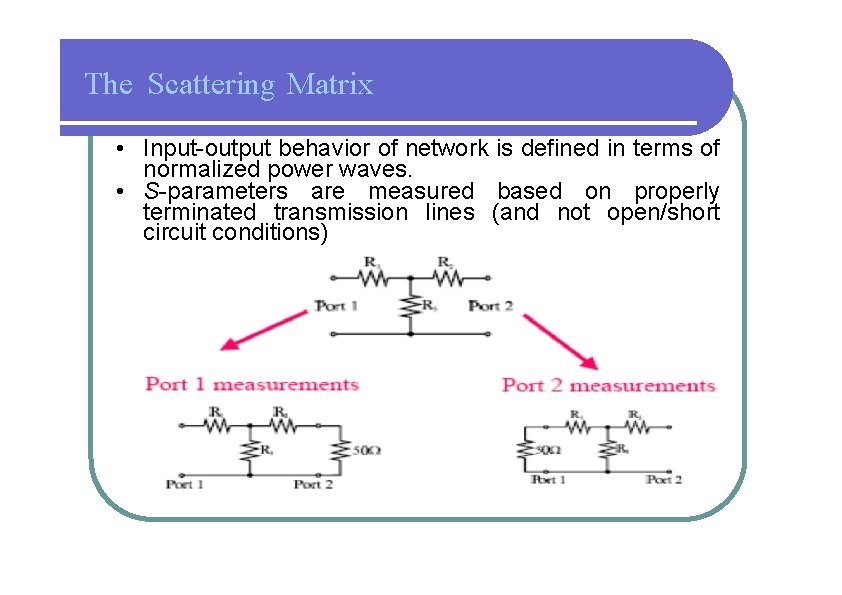
The Scattering Matrix • Input-output behavior of network is defined in terms of normalized power waves. • S-parameters are measured based on properly terminated transmission lines (and not open/short circuit conditions)

The Scattering Matrix

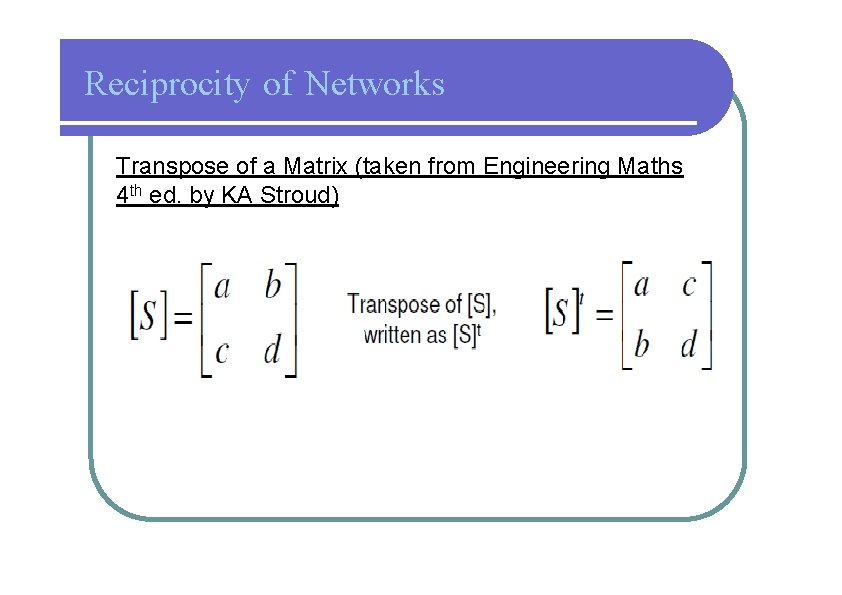
Reciprocity of Networks Reciprocal and symmetric networks “A network is reciprocal if a zero impedance source and a zero impedance ammeter can be placed at any locations in a network and their positions interchanged without changing the ammeter reading” - Lorentz Reciprocity results with network elements that are linear and bilateral; they have the same behavior for currents flowing in either direction. A symmetric network happens when: [s] = [s]t (4. 6 a)

Reciprocity of Networks Transpose of a Matrix (taken from Engineering Maths 4 th ed. by KA Stroud)

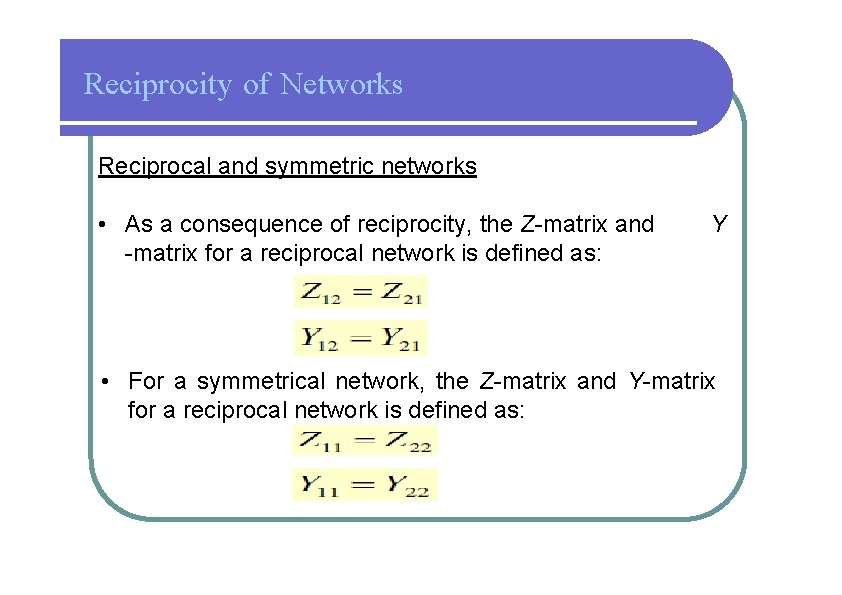
Reciprocity of Networks Reciprocal and symmetric networks • As a consequence of reciprocity, the Z-matrix and -matrix for a reciprocal network is defined as: Y • For a symmetrical network, the Z-matrix and Y-matrix for a reciprocal network is defined as:

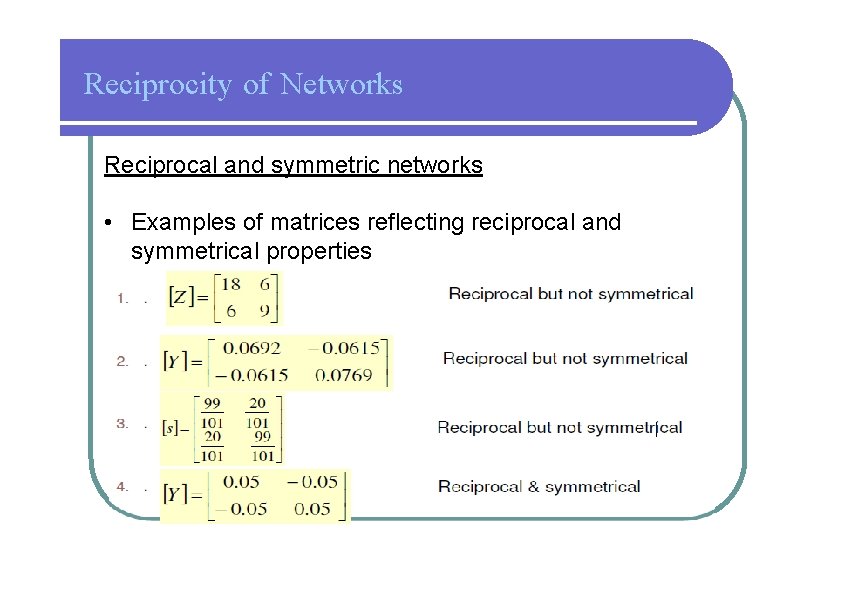
Reciprocity of Networks Reciprocal and symmetric networks • Examples of matrices reflecting reciprocal and symmetrical properties

Reciprocity of Networks Reciprocal and symmetric networks • Summary of reciprocity and symmetry:

Lossless Networks Lossless networks • A lossless network happens when: (4. 6 b) • It is also purely imaginary for lossless network (no real power can be delivered to the network). • A matrix that satisfies the condition of (4. 6 b) is called a unitary matrix, which can be re-written as: (4. 7)

Lossless Networks Lossless networks (Contd. ) • Which also can be re-written (for a 2 -port network): • Examples of lossless matrices;

Lossless Networks Lossless networks (Contd. ) • Proof? This circuit is symmetrical as well as reciprocal.

Lossless Networks Lossless networks (Contd. ) Example 1 • Proof that the S parameter below is unitary (lossless)

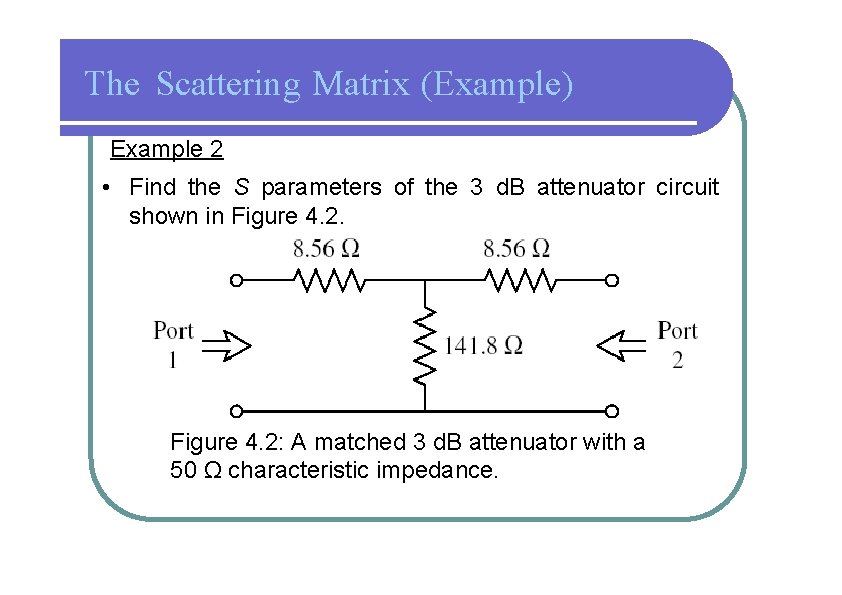
The Scattering Matrix (Example) Example 2 • Find the S parameters of the 3 d. B attenuator circuit shown in Figure 4. 2: A matched 3 d. B attenuator with a 50 Ω characteristic impedance.

The Scattering Matrix (Example) • From the following formula, S 11 can be found as the reflection coefficient seen at port 1 when port 2 is terminated with a matched load (Z 0 =50 Ω); • The equation becomes;

The Scattering Matrix (Example) • To calculate Zin(1), we can use the following formula; • Thus S 11 = 0. Because of the symmetry of the circuit, S 22 = 0. • S 21 can be found by applying an incident wave at port 1, V 1+, and measuring the outcome at port 2, V 2 -. This is equivalent to the transmission coefficient from port 1 to port 2:

The Scattering Matrix (Example) • From the fact that S 11 = S 22 = 0, we know that V 1 - = 0 when port 2 is terminated in Z 0 = 50Ω, and that V 2+ = 0. In this case we have V 1+ = V 1 and V 2 - = V 2. • Where 41. 44 = (141. 8//58. 56) is the combined resistance of 50Ω and 8. 56Ω paralled with the 141. 8Ω resistor. Thus, S 21 = S 12 = 0. 707.

The Scattering Matrix (Example) Example 3 • A two port network is known to have the following scattering matrix: a) Determine if the network is reciprocal and lossless. b) If port 2 is terminated with a matched load, what is the return loss seen at port 1? c) If port 2 is terminated with a short circuit, what is the return loss seen at port 1?

The Scattering Matrix (Example) • Q: Determine if the network is reciprocal and lossless. • From the matrix, [S] is not symmetric and not reciprocal. To determine whether it is lossless; So the network is not lossless. • Q: If port two is terminated with a matched load, what is the return loss seen at port 1? • When port 2 is terminated with a matched load, the reflection coefficient seen at port 1 is Γ = S 11 = 0. 15. So the return loss is; RL = − 20 log | G |= − 20 log(0. 15) =16. 5 d. B

The Scattering Matrix (Example) • Q: If port two is terminated with a short circuit, what is the return loss seen at port 1? • When port 2 is terminated with a short circuit, the reflection coefficient seen at port 1 can be found as follow. • From the definition of the scattering matrix and the fact that V 2+ = - V 2 - (for a short circuit at port 2), we can write:

The Scattering Matrix (Example) • The second equation gives; • Dividing the first equation by V 1+ and using the above result gives the reflection coefficient seen as port 1 as;

The Scattering Matrix (Example) • The return loss is; RL = -20 log 10|G|= -20 log 10(0. 452) = 6. 9 d. B • Important points to note: § Reflection coefficient looking into port n is not equal to Snn, unless all other ports are matched. § Transmission coefficient from port m to port n is not equal to Snm, unless all other ports are matched. § S parameters of a network are properties only of the network itself (assuming the network is linear). § It is defined under the condition that all ports are matched. § Changing the termination or excitation of a network does not change its S parameters, but may change the reflection coefficient seen at a given