PGT 104 DIGITAL ELECTRONICS COMBINATIONAL ARITHMETIC CIRCUITS PGT

PGT 104: DIGITAL ELECTRONICS COMBINATIONAL ARITHMETIC CIRCUITS PGT 104 DIGITAL ELECTRONICS

Combinational Arithmetic Circuits �Addition �Half-Adder �Full-Adder �Parallel Binary Adder �Comparator �Decoder �Encoder �Multiplexer �Demultiplexer PGT 104 DIGITAL ELECTRONICS

Half-Adder �Basic rules for binary addition: � 0 + 0 = 0 � 0 + 1 = 1 � 1 + 0 = 1 � 1 + 1 = 10 Sum of 0 with a carry of 0 Sum of 1 with a carry of 0 Sum of 0 with a carry of 1 �Operations are performed by a logic circuit called a half-adder. �Half-adder accepts two binary digits on its input and produces two binary digits on its outputs, a sum bit and a carry bit. PGT 104 DIGITAL ELECTRONICS

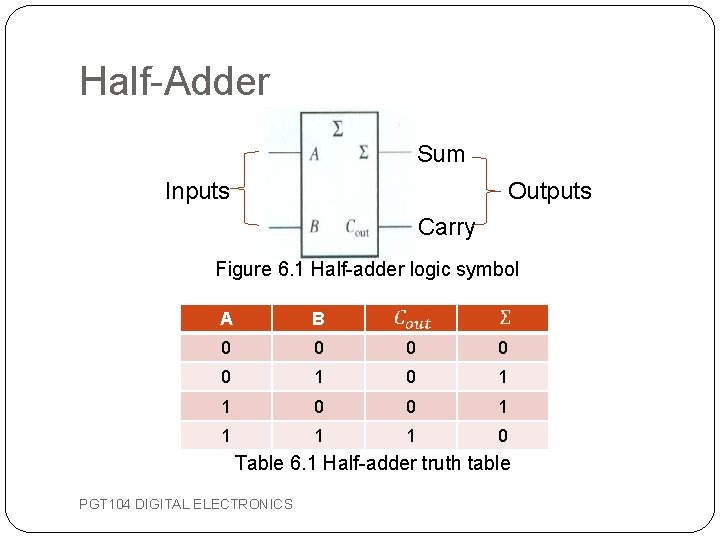
Half-Adder Sum Inputs Outputs Carry Figure 6. 1 Half-adder logic symbol A B 0 0 0 1 1 0 Table 6. 1 Half-adder truth table PGT 104 DIGITAL ELECTRONICS

Half-Adder �The sum output (∑) is a 1 if the input variables, A and B, are not equal. It can be expressed as the exclusive OR of the input variables. �The output carry (Cout) carry is a 1 only when both A and B are 1 s. It can be expressed as the AND of the input variables. Figure 6. 2 Half-adder logic diagram PGT 104 DIGITAL ELECTRONICS

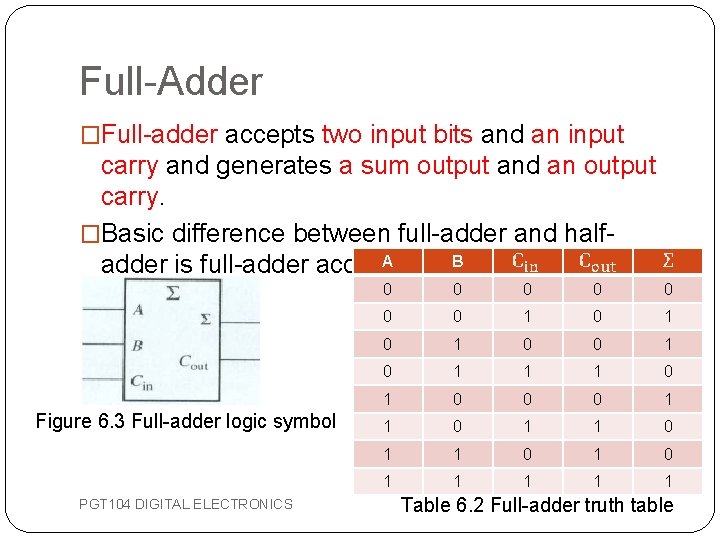
Full-Adder �Full-adder accepts two input bits and an input carry and generates a sum output and an output carry. �Basic difference between full-adder and half. A an input B adder is full-adder accepts carry. Figure 6. 3 Full-adder logic symbol PGT 104 DIGITAL ELECTRONICS 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 Table 6. 2 Full-adder truth table

Full-Adder �The full-adder must add the two input bits and the input carry. The sum output of the full-adder is: �The output carry (Cout) is a 1 when both inputs the first XOR gate are 1 s or when both inputs to the second XOR gate are 1 s. So the output carry can be expressed as: PGT 104 DIGITAL ELECTRONICS

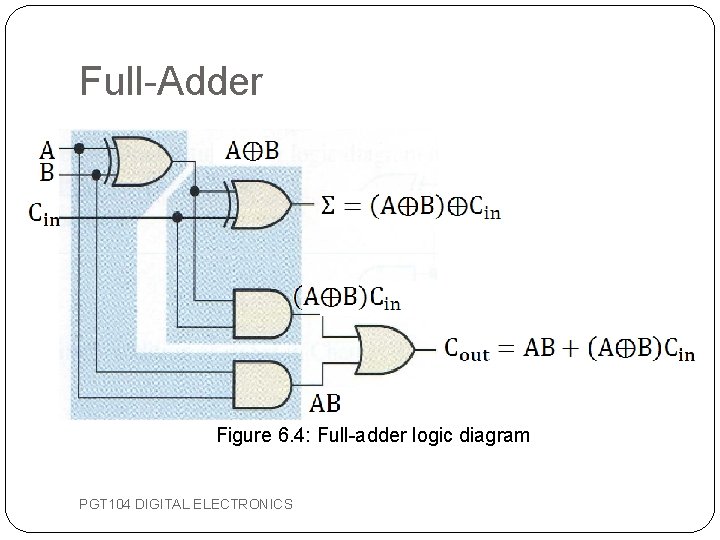
Full-Adder Figure 6. 4: Full-adder logic diagram PGT 104 DIGITAL ELECTRONICS

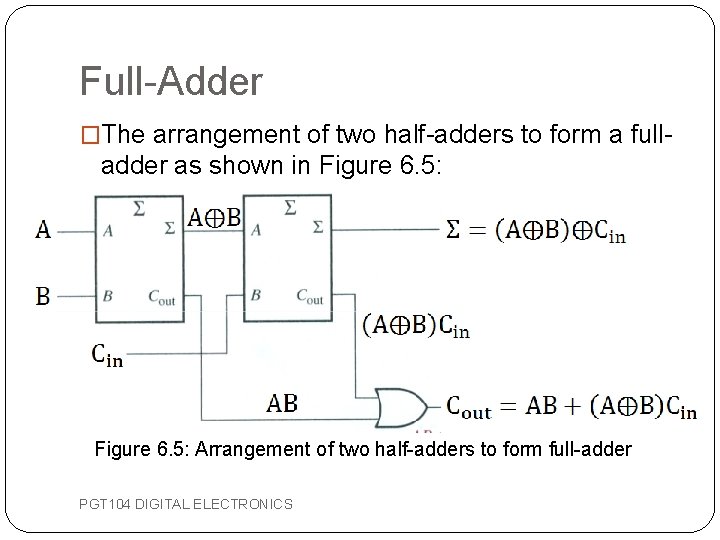
Full-Adder �The arrangement of two half-adders to form a full- adder as shown in Figure 6. 5: Arrangement of two half-adders to form full-adder PGT 104 DIGITAL ELECTRONICS

Parallel Binary Adders �Binary numbers with more than one bit must use additional full adders in order to perform addition operation. �When one binary added to another, each column generates a sum bit and a 1 or 0 carry bit to next 1 Carry bit column to the left. 0 11 from right �For example: +01 100 Carry bit from 2 nd column becomes a sum bit PGT 104 DIGITAL ELECTRONICS column

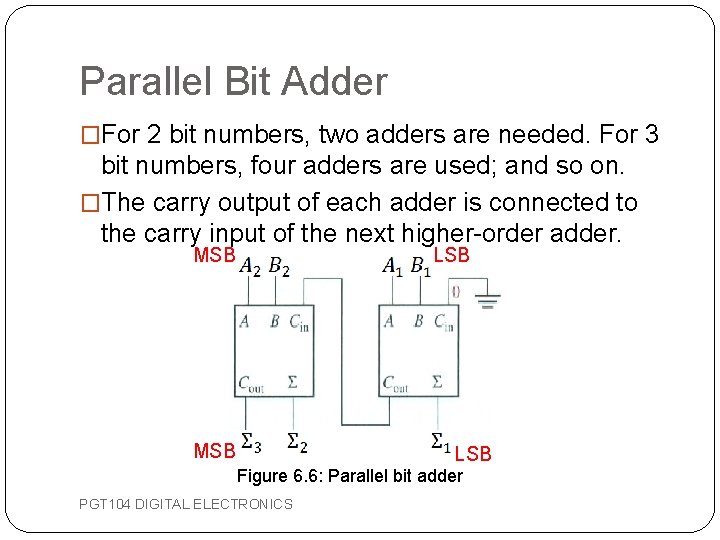
Parallel Bit Adder �For 2 bit numbers, two adders are needed. For 3 bit numbers, four adders are used; and so on. �The carry output of each adder is connected to the carry input of the next higher-order adder. LSB MSB LSB Figure 6. 6: Parallel bit adder PGT 104 DIGITAL ELECTRONICS

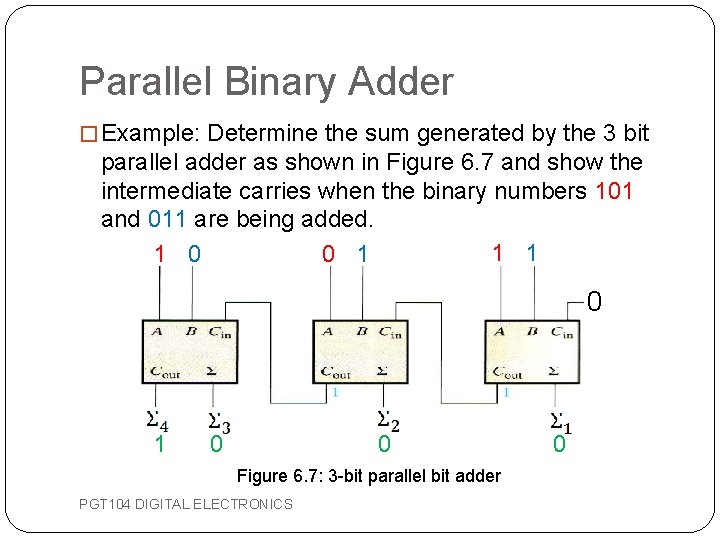
Parallel Binary Adder � Example: Determine the sum generated by the 3 bit parallel adder as shown in Figure 6. 7 and show the intermediate carries when the binary numbers 101 and 011 are being added. 1 1 1 0 0 Figure 6. 7: 3 -bit parallel bit adder PGT 104 DIGITAL ELECTRONICS 0

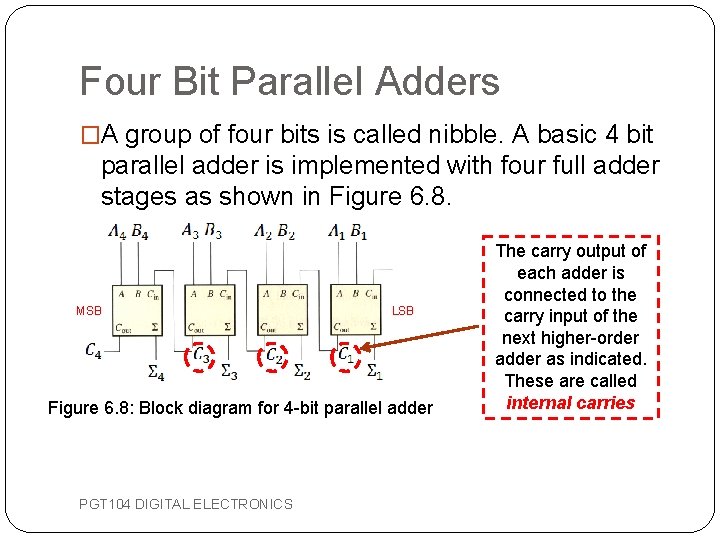
Four Bit Parallel Adders �A group of four bits is called nibble. A basic 4 bit parallel adder is implemented with four full adder stages as shown in Figure 6. 8. MSB LSB Figure 6. 8: Block diagram for 4 -bit parallel adder PGT 104 DIGITAL ELECTRONICS The carry output of each adder is connected to the carry input of the next higher-order adder as indicated. These are called internal carries

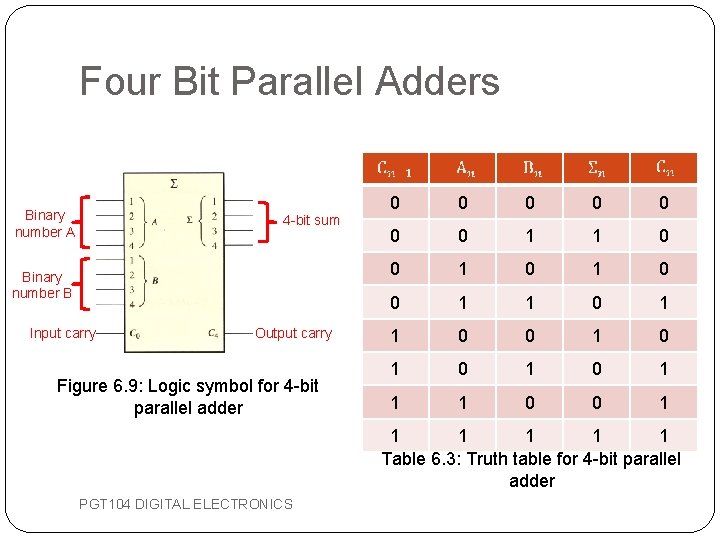
Four Bit Parallel Adders Binary number A 4 -bit sum Binary number B Input carry Output carry Figure 6. 9: Logic symbol for 4 -bit parallel adder 0 0 0 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 Table 6. 3: Truth table for 4 -bit parallel adder PGT 104 DIGITAL ELECTRONICS

Comparators �To compare the magnitudes of two binary quantities to determine the relationship of those quantities. �Determine whether two numbers are equal or not. PGT 104 DIGITAL ELECTRONICS

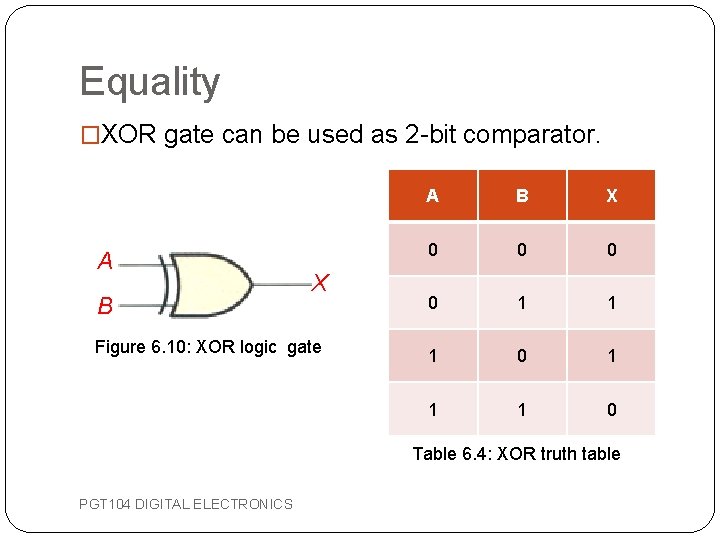
Equality �XOR gate can be used as 2 -bit comparator. A B X Figure 6. 10: XOR logic gate A B X 0 0 1 1 1 0 Table 6. 4: XOR truth table PGT 104 DIGITAL ELECTRONICS

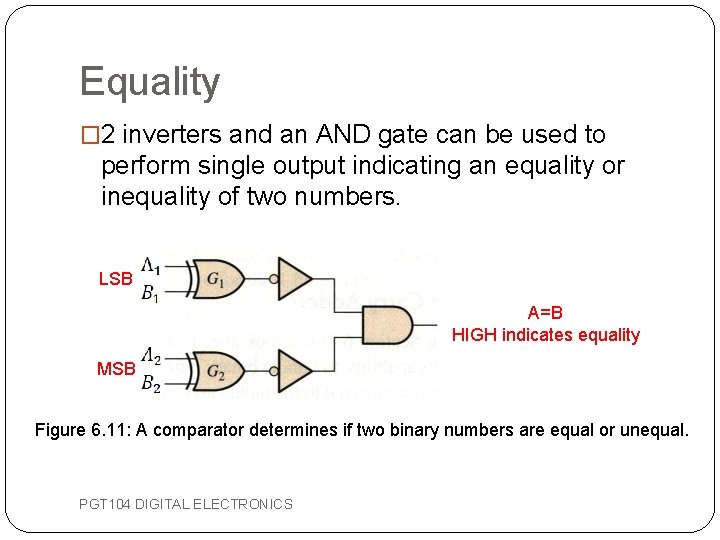
Equality � 2 inverters and an AND gate can be used to perform single output indicating an equality or inequality of two numbers. LSB A=B HIGH indicates equality MSB Figure 6. 11: A comparator determines if two binary numbers are equal or unequal. PGT 104 DIGITAL ELECTRONICS

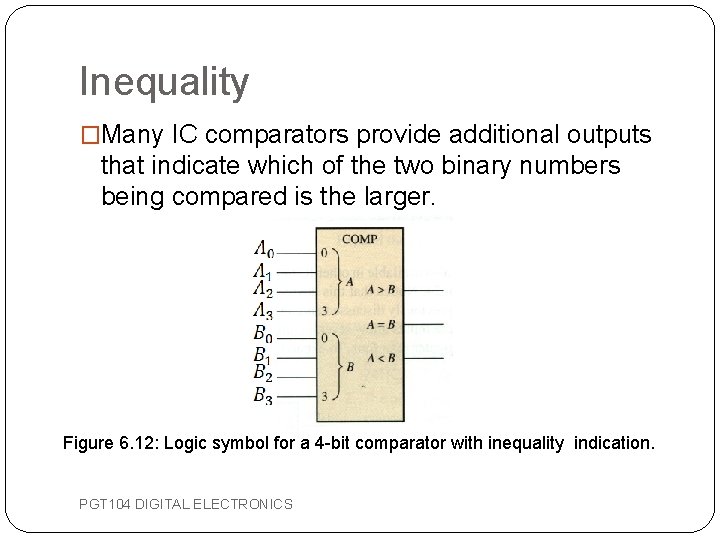
Inequality �Many IC comparators provide additional outputs that indicate which of the two binary numbers being compared is the larger. Figure 6. 12: Logic symbol for a 4 -bit comparator with inequality indication. PGT 104 DIGITAL ELECTRONICS

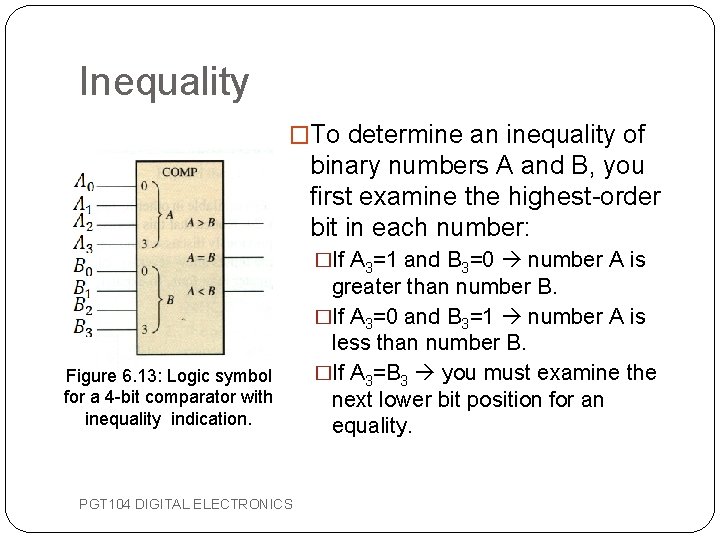
Inequality �To determine an inequality of binary numbers A and B, you first examine the highest-order bit in each number: �If A 3=1 and B 3=0 number A is Figure 6. 13: Logic symbol for a 4 -bit comparator with inequality indication. PGT 104 DIGITAL ELECTRONICS greater than number B. �If A 3=0 and B 3=1 number A is less than number B. �If A 3=B 3 you must examine the next lower bit position for an equality.

Decoders �A decoder detects the presence of a specified combination of bits (code) on its inputs and indicates the presence of that code by a specified output level. �In its general form, a decoder has n input lines to handle n bits and forms one to 2 n output lines to indicate the presence of one or more n-bit combinations. PGT 104 DIGITAL ELECTRONICS

Basic Binary Decoder �An AND gate can be used as the basic decoding element because it produces a HIGH output only when all of its inputs are HIGH. Therefore, all of the inputs to the AND gate are HIGH. PGT 104 DIGITAL ELECTRONICS

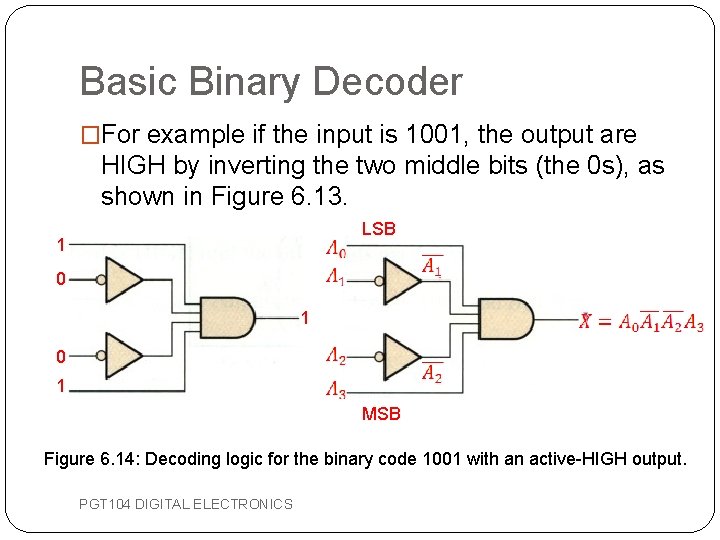
Basic Binary Decoder �For example if the input is 1001, the output are HIGH by inverting the two middle bits (the 0 s), as shown in Figure 6. 13. LSB 1 0 1 MSB Figure 6. 14: Decoding logic for the binary code 1001 with an active-HIGH output. PGT 104 DIGITAL ELECTRONICS

Basic Binary Decoder �Example: Determine the logic required to decode binary number 1011 by producing a HIGH level on the output based on logic diagram given below. �Solution: Input = 1011 = �The 3 rd bit ( ) needs tp invert in order to produce HIGH level output. Figure 6. 15: Logic diagram for corresponding decoder PGT 104 DIGITAL ELECTRONICS

4 -Bit Decoder �In order to decode all possible combinations of four bits, 16 decoding gates are required (24=16). �This type of decoder is commonly called either: �A 4 -line-to-16 -line decoder, or �A 1 -of-16 decoder. Figure 6. 16: Logic symbol for a 4 -line-to 16 -line (1 -or-16) decoder. PGT 104 DIGITAL ELECTRONICS

4 -Bit Decoder Table 6. 5: Decoding functions and truth table for a 4 -line-to-16 -line decoder with active-LOW outputs. PGT 104 DIGITAL ELECTRONICS

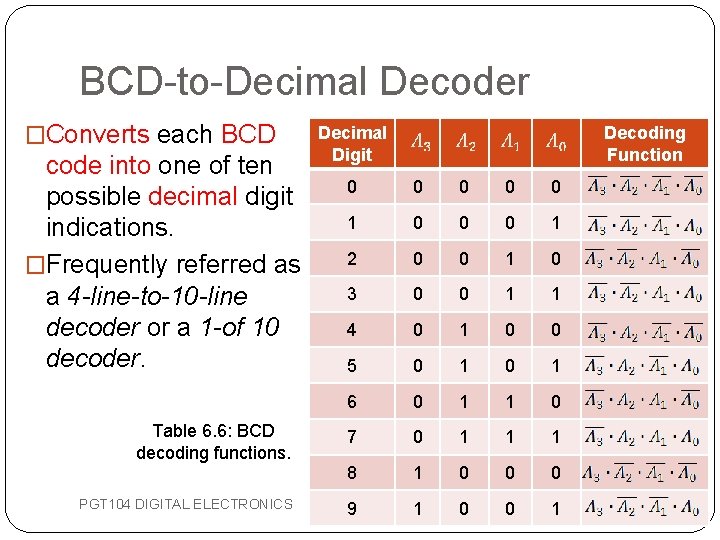
BCD-to-Decimal Decoder �Converts each BCD code into one of ten possible decimal digit indications. �Frequently referred as a 4 -line-to-10 -line decoder or a 1 -of 10 decoder. Table 6. 6: BCD decoding functions. PGT 104 DIGITAL ELECTRONICS Decimal Digit Decoding Function 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1

BCD-to-7 -Segment Decoder Output lines connect to 7 -segment display device �The BCD-to-7 - segment decoder accepts the BCD code on its inputs and provides outputs to drive 7 segment display devices to produce a decimal readout. BCD input Figure 6. 17: Logic symbol for BCD-to 7 -segment with active-LOW outputs. PGT 104 DIGITAL ELECTRONICS

Encoders �An encoder is a combinational logic circuit that essentially performs a “reverse” decoder function. �An encoder accepts an active level on one of its inputs representing a digit, such as a decimal or octal digit, and converts it to a coded output such as BCD or binary. �Encoders can also be devised to encode various symbols and alphabetic characters. PGT 104 DIGITAL ELECTRONICS

Decimal-to-BCD Encoder �It has 10 inputs and 4 outputs corresponding to the BCD code. Decimal input BCD output Figure 6. 18: Logic symbol for decimal-to-BCD encoder PGT 104 DIGITAL ELECTRONICS

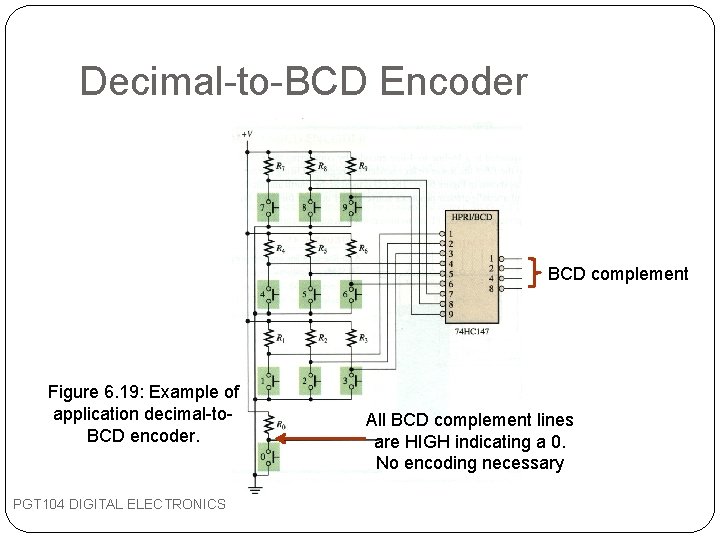
Decimal-to-BCD Encoder BCD complement Figure 6. 19: Example of application decimal-to. BCD encoder. PGT 104 DIGITAL ELECTRONICS All BCD complement lines are HIGH indicating a 0. No encoding necessary

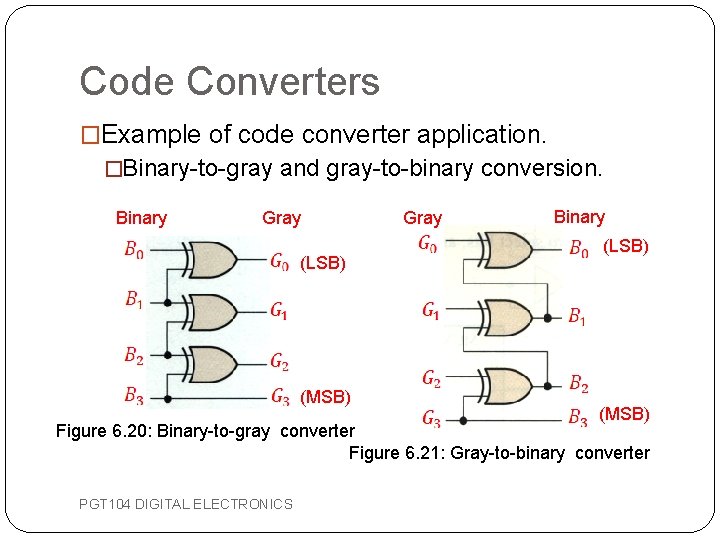
Code Converters �Example of code converter application. �Binary-to-gray and gray-to-binary conversion. Binary Gray (LSB) (MSB) Gray Binary (LSB) (MSB) Figure 6. 20: Binary-to-gray converter Figure 6. 21: Gray-to-binary converter PGT 104 DIGITAL ELECTRONICS

Multiplexers �A MUX is a device that allows digital information from several sources to be routed onto a single line for data transmission over that line to a common destination. �The basic MUX has several data-input lines and a single output line. �It also has data-select inputs, which permit digital data on any one of the inputs to be switched to the output line. �Also known as data selectors. PGT 104 DIGITAL ELECTRONICS

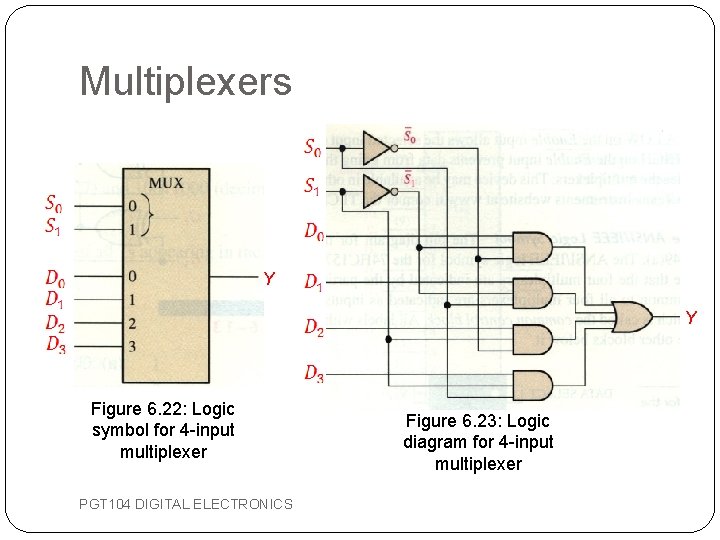
Multiplexers Y Y Figure 6. 22: Logic symbol for 4 -input multiplexer PGT 104 DIGITAL ELECTRONICS Figure 6. 23: Logic diagram for 4 -input multiplexer

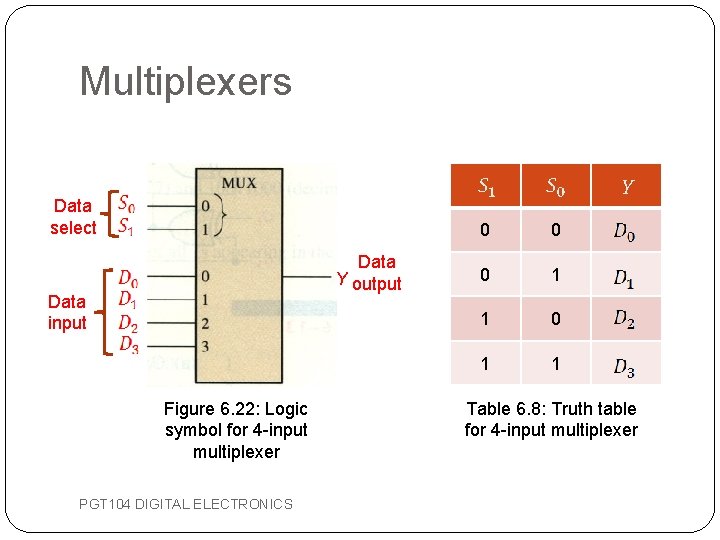
Multiplexers Data select Data Y output Data input Figure 6. 22: Logic symbol for 4 -input multiplexer PGT 104 DIGITAL ELECTRONICS 0 0 0 1 1 Table 6. 8: Truth table for 4 -input multiplexer

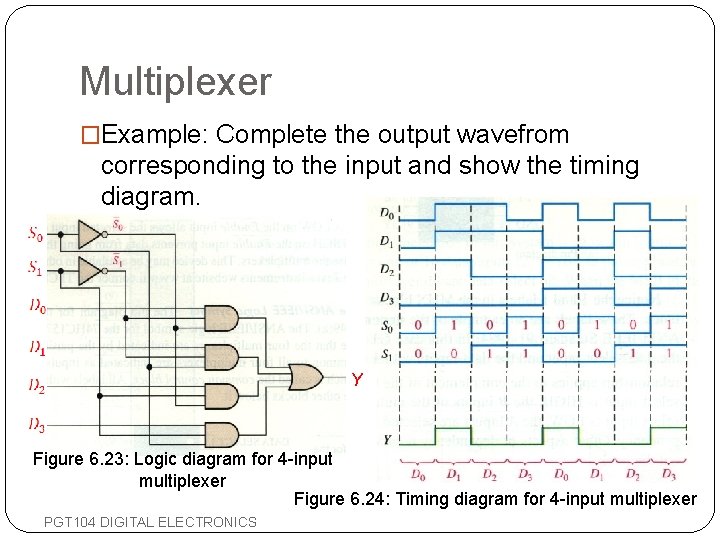
Multiplexer �Example: Complete the output wavefrom corresponding to the input and show the timing diagram. Y Figure 6. 23: Logic diagram for 4 -input multiplexer Figure 6. 24: Timing diagram for 4 -input multiplexer PGT 104 DIGITAL ELECTRONICS

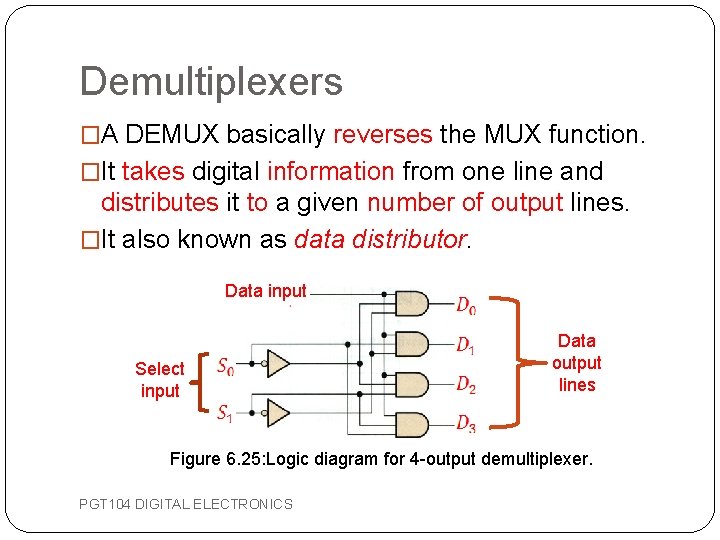
Demultiplexers �A DEMUX basically reverses the MUX function. �It takes digital information from one line and distributes it to a given number of output lines. �It also known as data distributor. Data input Select input Data output lines Figure 6. 25: Logic diagram for 4 -output demultiplexer. PGT 104 DIGITAL ELECTRONICS

THE END PGT 104 DIGITAL ELECTRONICS